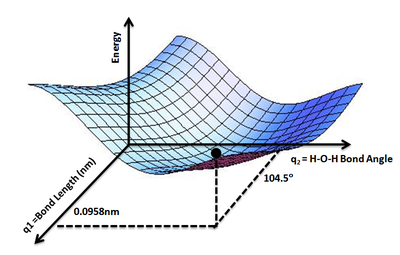
퍼텐셜 에너지 표면

Potential energy surface

PES(Potential Energy Surface)는 시스템의 에너지, 특히 원자의 집합, 일반적으로 원자의 위치에 대한 특정 매개변수의 관점에서 설명합니다.표면은 에너지를 하나 이상의 좌표에 대한 함수로 정의할 수 있습니다. 좌표가 하나만 있는 경우 표면은 잠재적 에너지 곡선 또는 에너지 프로필이라고 합니다.예를 들어 모스/장거리 전위가 있습니다.

풍경의 유추는 도움이 됩니다.두 개의 자유도(예를 들어 두 개의 결합 길이)를 가진 시스템의 경우 에너지 값(아날로그: 땅의 높이)은 두 개의 결합 길이 함수입니다(아날로그: [1]지면 위치의 좌표).

물 분자의 PES:물-O-H 결합길이 0.0958nm, H-O-H 결합각 104.5에 대한 최적화된 분자구조에 해당하는 에너지 최소값을 나타낸다.°

PES의 개념은 화학과 물리 같은 분야, 특히 이러한 과목의 이론적인 하위 분야들에서 응용된다.그것은 이론적으로 분자의 최소 에너지 형태를 찾거나 화학 반응 속도를 계산하는 것과 같이 원자로 구성된 구조의 특성을 탐구하는데 사용될 수 있다.

수학적 정의와 계산

원자의 집합의 형상은 원자의 위치를 나타내는 벡터 r로 설명할 수 있다.벡터 r은 원자의 데카르트 좌표의 집합일 수도 있고 원자간 거리와 각도의 집합일 수도 있다.

주어진 r에서 위치 함수로서의 에너지 E(r)는 모든 관심 r에 대한 E(r)의 값이다.도입부의 풍경 유추를 이용하여 E는 "에너지 풍경"의 높이를 제시하여 잠재적 에너지 표면의 개념이 발생하도록 한다.

PES를 원자 위치의 함수로 사용하는 화학 반응을 연구하려면 모든 원자 배열에 대한 에너지를 계산할 필요가 있다.원자의 특정 원자 배열의 에너지를 계산하는 방법은 계산 화학 기사에 잘 설명되어 있으며, 여기서 강조되는 것은 세분화된 에너지 위치 정보를 산출하기 위한 E(r)의 근사치를 찾는 것입니다.

매우 단순한 화학 시스템의 경우 또는 원자간 상호작용에 대한 근사치를 단순화할 때, 때때로 원자 위치의 함수로서 에너지에 대해 분석적으로 도출된 식을 사용할 수 있다.예를 들어, 3개의 H-H 거리의 함수로서 시스템 H + H에2 대한 London-Eyring-Polanyi-Sato 전위가[2][3][4] 있습니다.

보다 복잡한 시스템의 경우, 원자의 특정 배열의 에너지 계산은 종종 너무 계산적으로 비싸서 표면의 대규모 표현이 실현 가능하지 않다.이러한 시스템의 경우 가능한 접근법은 PES의 축소된 포인트 세트만 계산한 다음,[5] 예를 들어 Shepard 보간법과 같이 계산적으로 더 저렴한 보간법을 사용하여 공백을 메우는 것이다.

어플

PES는 분자 기하학과 화학 반응 역학의 분석을 지원하는 개념적인 도구입니다.PES 상에서 필요한 포인트를 평가한 후에는 위치에 관한 에너지의 제1 및 제2 도함수에 따라 포인트를 분류할 수 있으며, 각각 구배와 곡률이다.정지점(또는 기울기가 0인 점)은 물리적 의미를 갖는다. 에너지 최소점은 물리적으로 안정된 화학종에 대응하고 안장점은 반응 좌표의 가장 높은 에너지점(화학 반응물을 화학 제품에 연결하는 가장 낮은 에너지 경로)인 전이 상태에 대응한다.

매력적이고 혐오스러운 표면

화학반응을 위한 잠재적 에너지 표면은 활성착체 내의 결합길이 확장을 반응물 및 [6][7]생성물의 길이와 비교함으로써 매력적 또는 거부적으로 분류할 수 있다.A + B - C → A - B + C의 반응에서 새로 형성된 A - B 결합의 결합 길이 확장은 R*AB = RAB - R로0AB 정의되며, 여기서AB R은 전이 상태의 A - B 결합 길이0AB, R은 제품 분자 내의 R이다.마찬가지로 반응에서 분해되는 결합에 대해서도 R*BC = RBC - R이며0BC, 여기서0BC R은 반응물 [8]분자를 의미한다.

발열 반응의 경우, ABPES는 R*BC > R*일 경우 매력적(또는 조기 다운힐)으로 분류되므로 반응물이 서로 접근하고 있을 때 전이 상태에 도달한다.전이 상태 후, A-B 결합 길이는 계속 감소하기 때문에 자유 반응 에너지의 상당 부분이 A-B [8][9]결합의 진동 에너지로 변환됩니다.예를 들어, 작살 반응 K2 + Br → K—Br + Br - 반응물의 초기 장거리 흡인력이 K••Br−••[8]Br과 유사한+ 활성 복합체로 이어지는 경우.제품 분자의 진동 들뜸 집단은 적외선 화학발광으로 [10][11]검출할 수 있다.

반면, H + Cl2 → HCl + Cl 반응에 대한 PES는 R*HCl < R*ClCl 및 생성물이 [8][9]분리될 때 전이 상태에 도달하기 때문에 반발(또는 후발)이 있다.원자 A(여기서 H)가 B 및 C보다 가벼운 이 반응에 대해 반응 에너지는 주로 [8]생성물의 변환 운동 에너지로 방출된다.원자 A가 B 및 C보다 무거운 F + H2 → HF + H와 같은 반응에 대해서는 PES가 [8]반발성이지만 진동과 변환의 혼합 에너지 방출이 있다.

흡열 반응의 경우 표면의 종류에 따라 반응을 일으키는 데 가장 효과적인 에너지의 종류가 결정됩니다.반응물의 번역 에너지는 매력적인 표면과의 반응을 유도하는 데 가장 효과적이며, 반발면과의 [8]반응에는 진동 들뜸(높은 진동 양자수 v에 대한)이 더 효과적이다.후자의 예로서 동일한 HCl의 [12]총 에너지에서 F + HCl(v=1) → Cl + HF 반응은 F + HCl(v=0) → Cl + HF보다 약 5배 빠르다.

역사

화학 반응을 위한 잠재적 에너지 표면의 개념은 [13]1913년 프랑스의 물리학자 르네 마르셀랭에 의해 처음 제안되었다.헨리 에링과 마이클 폴라니는 1931년 H+H2 반응에 대해 잠재적 에너지 표면의 첫 반경험적 계산을 제안했다.아이링은 1935년 전이 상태 이론에서 반응 속도 상수를 계산하기 위해 위치 에너지 표면을 사용했습니다.


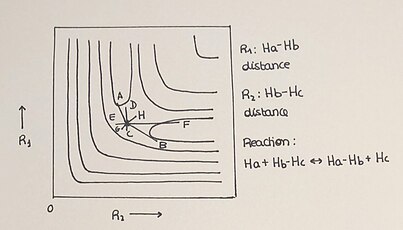
H + H2 2차원 PES

위치 에너지 표면은 일반적으로 3차원 그래프로 표시되지만, 2차원 그래프로도 나타낼 수 있다. 이 그래프는 반응의 진보를 등 에너지 라인을 사용하여 플롯한다.공선계 H + H는2 2차원 PES를 쉽고 알기 쉽게 표시할 수 있는 단순한 반응이다.이 반응에서 수소원자(H)는 분자로부터의 1개의 원자와 새로운 결합을 형성함으로써 수소분자2(H)와 반응하고, 이것은 다시 원래의 분자의 결합을 끊는다.이는 H + Hb–Hc → Ha–Hb + H로ac 상징된다. 반응물질(H+Hants)에서 생성물(H-H)로의 반응 진행과 반응에 참여하는 종의 에너지는 해당 잠재적 에너지 표면에서 잘 정의된다.에너지 프로파일은 위치 에너지를 기하학적 변수의 함수로 설명한다(모든 차원의 PES는 시간과 온도에 의존하지 않는다).

H+H2 퍼텐셜 에너지 표면

2-D PES에는 다양한 관련 요소가 있습니다.

  • 2-D 그림은 반응물을 찾는 최소 지점, 제품 및 안장 지점 또는 전환 상태를 보여 줍니다.
  • 전이 상태는 반응 좌표의 최대값과 반응 경로에 수직인 좌표의 최소값입니다.
  • 시간의 진보는 모든 반응의 궤적을 묘사한다.반응 조건에 따라 공정은 두 축 사이에 표시된 생성물 형성에 도달하는 다양한 방법을 보여줍니다.

「 」를 참조해 주세요.

레퍼런스

  1. ^ 화학 용어집 제2판의 전위 에너지(반응) 표면. ('골드북').A. D. McNaught와 A.에 의해 편집되었습니다.윌킨슨.블랙웰 사이언티픽 퍼블리케이션, 옥스퍼드(1997년)
  2. ^ Sato, S. (1955). "A New Method of Drawing the Potential Energy Surface". Bulletin of the Chemical Society of Japan. 28 (7): 450–453. doi:10.1246/bcsj.28.450.Sato, Shin (1955). "On a New Method of Drawing the Potential Energy Surface". The Journal of Chemical Physics. 23 (3): 592–593. Bibcode:1955JChPh..23..592S. doi:10.1063/1.1742043.
  3. ^ Keith J. Laidler, Chemical Kinetics (제3판, Harper & Row 1987) p.68-70 ISBN 0-06-043862-2
  4. ^ 스타인펠트 J.I., 프란시스코 J.S., 하세 W.L.화학 동역학 (2차 1998년판, 프렌티스홀) p.201-2 ISBN 0-13-737123-3
  5. ^ 이동 최소 제곱 강화 셰퍼드 보간법 빠른 행진 및 현악기, 버거 SK1, 류 Y, 사르카 U, 에어스 PW, J Chem Phys. 2009 130 (2) 024103.doi: 10.1063/1.2996579.
  6. ^ 화학 용어집 제2판의 매력적인 전위 에너지 표면. ('골드북').A. D. McNaught와 A.에 의해 편집되었습니다.윌킨슨.블랙웰 사이언티픽 퍼블리케이션, 옥스퍼드(1997년)
  7. ^ 화학 용어집 제2판의 반발 전위 에너지 표면. ('골드북').A. D. McNaught와 A.에 의해 편집되었습니다.윌킨슨.블랙웰 사이언티픽 퍼블리케이션, 옥스퍼드(1997년)
  8. ^ a b c d e f g Keith J. Laidler, Chemical Kinetics (제3판, Harper & Row 1987) p.461-8 ISBN 0-06-043862-2
  9. ^ a b 스타인펠트 J.I., 프란시스코 J.S., 하세 W.L.화학 동태 및 역학 (제2판, 프렌티스홀 1998) p.272-4 ISBN 0-13-737123-3
  10. ^ 스타인펠트 J.I., 프란시스코 J.S., 하세 W.L.화학 동력과 역학 (제2판, 프렌티스홀 1998) 페이지 263 ISBN 0-13-737123-3
  11. ^ 앳킨스 P.와 드 폴라 J.물리화학(제8판, W.H.)Freeman 2006) 페이지 886 ISBN 0-7167-8759-8
  12. ^ 앳킨스 P.와 드 폴라 J.물리화학(제8판, W.H.)Freeman 2006) 페이지 889-890 ISBN 0-7167-8759-8
  13. ^ 계산 화학: Errol G. Lewars 분자 및 양자역학의 이론과 응용에 대한 소개, 제2판 (Springer 2011) 페이지 21 ISBN 978-9048138616