혼합 그래프

혼합 그래프 G = (V, E, A)는 정점(또는 노드) V, (간접) 에지 E, 방향 에지(또는 호) A의 집합으로 구성된 수학 객체다.^[1]

정의 및 표기법

Consider adjacent vertices ${\displaystyle u,v\in V}$. A directed edge, called an arc, is an edge with an orientation and can be denoted as ${\displaystyle {\overrightarrow {uv}}}$ or ${\displaystyle (u,v)}$ (note that ${\displaystyle u}$ is the tail and ${\displaystyle v}$ is the he호의 ^[2]광고또한, 비방향 에지 또는 에지는 방향이 없는 에지로서 ${\displaystyle u}$ v$${\$displaystyle uv}$${\displaystyle }$또는$$${\displaystyle }$[${\displaystyle u}$ , ${\displaystyle v}$ ${\displaystyle ]}$ ${\displaystyle [u,v]}$로 나타낼 수 있다$.$^[2]

우리의 적용 예제를 위해 우리는 혼합 그래프의 루프나 다중 에지는 고려하지 않을 것이다.

A walk in a mixed graph is a sequence ${\displaystyle v_{0},c_{1},v_{1},c_{2},v_{2},\dots ,c_{k},v_{k}}$ of vertices and edges/arcs such that for all indices ${\displaystyle i}$, either ${\displaystyle c_{i}=v_{i}v_{i+1}}$ is an그래프 ${\displaystyle {엣지}_{}\stackrel{}{{또는}_{}}}$ c i = ${\displaystyle \stackrel{}{{}_{}{}_{}}}$ v i${\displaystyle \stackrel{}{{}_{}}}$+${\displaystyle \stackrel{}{{}_{}}}$ → ${\$는 그래프의 호이다$$.이 걸음은 첫 번째 정점과 마지막 정점을 제외하고 가장자리, 호 또는 정점을 반복하지 않는 경우 경로다.경로는 첫 번째 정점과 마지막 정점이 같으면 닫히고, 닫힌 경로는 첫 번째 정점과 마지막 정점을 제외하고 정점을 반복하지 않으면 순환이다.혼합 그래프는 주기를 포함하지 않으면 반복적이다.

컬러링

혼합 그래프 색상은 혼합 그래프의 정점에 대한 라벨링 또는 k 다른 색상(여기서 k는 양의 정수)의 할당으로 생각할 수 있다.^[3]가장자리로 연결된 꼭지점에 다른 색상을 할당해야 한다.색상은 1부터 k까지의 숫자로 나타낼 수 있으며, 지시된 호의 경우 호의 꼬리는 호의 머리보다 작은 숫자로 색칠해야 한다.^[3]

예

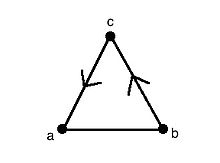
예를 들어, 오른쪽의 수치를 생각해 보십시오.혼합 그래프를 색칠하는 데 사용할 수 있는 k-색상은${\displaystyle }${${\displaystyle 1}$,${\displaystyle 2}$,${\displaystyle 3}$ ${\displaystyle \}}$ ${\displaystyle \{1,2,3\}}$ 입니다$.$ $u{\displaystyle }$ ${\displaystyle u}$과 $v{\displaystyle }$ ${\displaystyle v$$}$은(${\displaystyle }$ ${\displaysty u}$과 $}$은 각각 1과 2로 표시됨).$v{\displaystyle }$ ${\displaystyle v}$에서 $w{\displaystyle }$ ${\displaystyle$ w$}$까지의 호도 있다$.$ 방향은 순서를 지정하기 때문에 꼬리(${\displaystyle }$ ${\displaystyle$ v$\})$에 우리 호의 머리(${\displaystyle }$ ${\displaystyle w$보다 작은 색(또는 우리 세트의 정수)으로 라벨을 붙여야 한다.

색감이 강하고 약함

혼합 그래프의 적절한 k-색상은 함수다.

${\displaystyle c:$${\displaystyle V}$$\rightarrow [k]}$ 여기서$$ [${\displaystyle k\mathrm{}}{\displaystyle ]}$ : 1,${\displaystyle 2}$, ${\displaystyle \dots ,}$k ${\$$={1,2,\dots ,k}}$ such that ${\displaystyle c(u)\neq c(v)}$ if ${\displaystyle uv\in E}$ and ${\displaystyle c(u)<c(v)}$ if ${\displaystyle {\overrightarrow {uv}}\in A}$.^[1]

아크의 약한 조건을 적용할 수 있으며, 혼합 그래프의 약한 적절한 k-색상을 함수로 간주할 수 있다.

${\displaystyle c:$${\displaystyle V}$$\rightarrow [k]}$ 여기서$$ [${\displaystyle k\mathrm{}}{\displaystyle ]}$ : 1,${\displaystyle 2}$, ${\displaystyle \dots ,}$k ${\$={1,2,\dots ,k}}가 c(u)≠ c(v){\displaystyle c(u)\neq c(v)}만약 너의 v∈ E{\displaystyle uv\in E}과 c(u)≤ c(v){\displaystyle c(u)\leq c(v)}만약 너의 v→ ∈{\displaystyle{\overrightarrow{uv}}\in}.[1]을 가리키며 다시 우리의 예로, 이 의미하는 것은 우리가 할 수 있도록 라벨을 둘 다 머리와 꼬리의.${\displaystyle (v}$, ${\displaystyle w}$) ${\displaystyle(v,w)}($양수 정수 2$$).

존재

혼합 그래프에 색상이 있을 수도 있고 없을 수도 있다.혼합 그래프가 k-색상을 가지려면 그래프에 지시된 사이클이 포함될 수 없다.^[2]만약 그러한 k-색상이 존재한다면, 우리는 우리의 그래프를 ${\displaystyle \chi }$( G${\displaystyle }$) ${\displaystyle \chi (G)}$로 나타내는 색수로 적절히 색칠하기 위해 필요한 가장 작은 k를 가리킨다$.$^[2] 우리는 적절한 k-색상의 개수를 k의 다항 함수로 셀 수 있다.이것은 우리 그래프 G의 색다형 다항식(직접되지 않은 그래프의 색다형 다항식과 유사하게)이라고 불리며 $\chi {\displaystyle {}_{}}$ G${\displaystyle {}_{}}$(${\displaystyle k_{}}$) ${\displaystyle \chi _{G}(k)$로 나타낼 수 있다$.$^[1]

취약한 색도 다항식 계산

삭제-축소 방법은 혼합 그래프의 약한 색도 다항식을 계산하는 데 사용할 수 있다.이 방법에는 가장자리 또는 호를 삭제(또는 제거)하고 그 가장자리(또는 호)에 입사하는 나머지 정점을 수축(또는 결합)하여 하나의 꼭지점을 형성하는 것이 포함된다.^[4]로 G− e{G-e\displaystyle}.[4]우리는 가장자리, e{\displaystyle e}의 이 삭제를 나타낼 수 있{G=(V,E,A)\displaystyle}우리가 혼합된 그래프(V, E− e, A){\displaystyle(V,E-e,A)}를 얻게 된 그래프에서 가장자리, e{\displaystyle e}, 삭제 후 G)마찬가지로, 아크 삭제함으로써 a(V, E, A){\displaystyle}, 엇갈린 그래프에서, 우리는 우리는{G-a\displaystyle}.[4]− 또한, e{\displaystyle e}의 수축과 G/e{G/e\displaystyle}로{\displaystyle}를 나타낼 수 있는{\displaystyle}의 G로 삭제를 나타낼 수 있(V, E, A−){\displaystyle(V,E,A-a)}를 얻게 된다.${\displaystyle G}$/ ${\displaystyle 각각}$ ${\displaystyle G/a$^[4]제시된 제안에서 혼합 그래프의 색도 다항식을 계산하기 위해 다음과 같은 방정식을 얻는다.^[4]

1. ${\displaystyle {\chi }_{}}$ ${\displaystyle G_{}}$( ${\displaystyle k}$)${\displaystyle }$= ${\displaystyle {}_{}}$ ${\displaystyle G_{}}$- e (${\displaystyle {}_{}k}$) -${\displaystyle {}_{}}$ ${\displaystyle G_{}}$/ e ( ${\displaystyle k}$) ${\displaystyle \chi _{G}(k)=\chi$ _${G-e}-\chi _{G/e}(k$^[5]
2. ${\displaystyle {\chi }_{}}$ ${\displaystyle G_{}}$( ${\displaystyle k}$)${\displaystyle }$= ${\displaystyle {\chi }_{}}$ ${\displaystyle G_{}}$- a (${\displaystyle {}_{}k}$)${\displaystyle }$+ ${\displaystyle \chi }$ G${\displaystyle {}_{}}$/ a (${\displaystyle {}_{}{k}_{}}$) -${\displaystyle {}_{}}$ G ${\displaystyle {a_{}}_{}}$ (${\displaystyle {{}_{}}_{}k}$) ${\displaystyle \chi _{G}(k)=\chi$ _${G-a}+\chi _{G/a}-}-\chi _{G_${a$}}}}}}}}($k$)\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}($^[5]$k}.$

적용들

스케줄링 문제

혼합 그래프를 사용하여 특정 시간 제약에 따라 작업 모음이 수행되는 작업 공간 스케줄링 문제를 모델링할 수 있다.이러한 종류의 문제에서, 비방향 에지는 두 직무가 양립할 수 없는 제약조건을 모델링하는 데 사용될 수 있다(이들은 동시에 수행될 수 없다).지시된 가장자리는 한 작업이 다른 작업보다 먼저 수행되어야 하는 우선 순위 제약 조건을 모형화하는 데 사용될 수 있다.스케줄링 문제에서 이렇게 정의한 그래프를 이분법 그래프라고 한다.혼합 그래프 컬러링 문제는 모든 작업을 수행하기 위한 최소 길이의 일정을 찾는 데 사용할 수 있다.^[2]

베이시안 추론

혼합 그래프는 베이시안 추론의 그래픽 모델로도 사용된다.이런 맥락에서, Acyclic mixed graph(방향ed edge의 사이클이 없는 그래프)를 체인 그래프라고도 한다.이 그래프의 지시된 가장자리는 첫 번째 사건의 결과가 두 번째 사건의 확률에 영향을 미치는 두 사건 사이의 인과 관계를 나타내기 위해 사용된다.대신에 비방향 가장자리는 두 사건 사이의 비-주의 상관 관계를 나타낸다.체인 그래프의 비방향 서브그래프의 연결된 구성요소를 체인이라고 한다.체인 그래프는 도덕 그래프를 구성하여 비방향 그래프로 변형될 수 있으며, 동일한 체인에 발신 에지를 가진 정점 쌍 사이에 비방향 에지를 추가한 다음 지시된 에지의 방향을 잊음으로써 체인 그래프에서 형성된 비방향 그래프이다.^[6]

메모들

참조

• Beck, M.; Blado, D.; Crawford, J.; Jean-Louis, T.; Young, M. (2013), "On weak chromatic polynomials of mixed graphs", Graphs and Combinatorics, arXiv:1210.4634, doi:10.1007/s00373-013-1381-1.
• Cowell, Robert G.; Dawid, A. Philip; Lauritzen, Steffen L.; Spiegelhalter, David J. (1999), Probabilistic Networks and Expert Systems: Exact Computational Methods for Bayesian Networks, Springer-Verlag New York, p. 27, doi:10.1007/0-387-22630-3, ISBN 0-387-98767-3
• Hansen, Pierre; Kuplinsky, Julio; de Werra, Dominique (1997), "Mixed graph colorings", Mathematical Methods of Operations Research, 45 (1): 145–160, doi:10.1007/BF01194253, MR 1435900.
• Ries, B. (2007), "Coloring some classes of mixed graphs", Discrete Applied Mathematics, 155 (1): 1–6, doi:10.1016/j.dam.2006.05.004, MR 2281351.

외부 링크

• Weisstein, Eric W. "Mixed Graph". MathWorld.