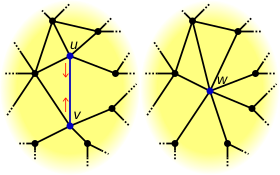
모서리 수축

그래프 이론에서 에지 수축은 이전에 결합한 두 정점을 동시에 병합하면서 그래프에서 에지를 제거하는 연산이다.가장자리 수축은 그래프 미성년자 이론의 근본적인 작동이다.정점 식별은 이 수술의 덜 제한적인 형태다.

정의

에지 수축 작업은 특정 에지($e{\displaystyle }$ ${\displaystyle$ e$})$에 대해 수행된다$.$에지 $e{\displaystyle }$ ${\displaystyle e}$이(가) 제거되고 그 $두{\displaystyle }$ 가지 인시던트 $정점$인$u$ {\displaystyle $u$$}$$$및 v {\$displaystyle$ v$}$이(가) $새로운{\displaystyle }$정점$$w {\$displaystyle$ w}에 대한 에지 인시던트가 각각$$ $u {\$$disks$} 또는$$$v{\displaystyle }$.$tyle v$ 보다 일반적으로 각 가장자리를 수축시켜 일련의 가장자리에서 작업을 수행할 수 있다(어떤 순서로든).^[1]

결과 유도된 그래프는 $때때로{\displaystyle }$G / ${\displaystyle e}${\$displaystyle$G/$e}$로 기록된다$.($$이{\displaystyle }$ 그래프를${\displaystyle }$에지 e ${\displaystyle$ G$\setminus$ e$\}$와 대조하여 에지 $e{\displaystyle }$ ${\displaysty$ e$}$을(를) 제거하십시오.)$$

아래에서 정의한 바와 같이, 에지 수축 연산은 원래 그래프가 단순 그래프였더라도 에지가 여러 개 있는 그래프를 초래할 수 있다.^[2]그러나 일부 저자들은^[3] 다중 가장자리 생성을 허용하지 않기 때문에 간단한 그래프에서 수행되는 가장자리 수축은 항상 간단한 그래프를 생성한다.

형식 정의

Let ${\displaystyle G=(V,E)}$ be a graph (or directed graph) containing an edge ${\displaystyle e=(u,v)}$ with ${\displaystyle u\neq v}$. Let ${\displaystyle f}$ be a function that maps every vertex in ${\displaystyle V\setminus \{u,v\}}$ to itself, and otherwise, maps$새로운{\displaystyle }$ 꼭지점 w ${\displaystyle w}$에 연결$.$The contraction of ${\displaystyle e}$ results in a new graph ${\displaystyle G'=(V',E')}$, where ${\displaystyle V'=(V\setminus \{u,v\})\cup \{w\}}$, ${\displaystyle E'=E\setminus \{e\}}$, and for every ${\displaystyle x\in V}$, $$${\displaystyle x'=f(x)\in V'}$ is incident to an edge ${\displaystyle e'\in E'}$ if and only if, the corresponding edge, ${\displaystyle e\in E}$ is incident to ${\displaystyle x}$ in ${\displaystyle G}$.

정점 식별

정점 식별(정점 수축이라고도 함)은 입사 모서리를 공유하는 정점에 걸쳐 수축이 발생해야 한다는 제한을 제거한다.(따라서, 가장자리 수축은 꼭지점 식별의 특별한 경우)연산은 그래프에서 정점 쌍(또는 부분 집합)에서 발생할 수 있다.두 수축 정점 사이의 가장자리는 때때로 제거된다.$v{\displaystyle }$ ${\displaystyle v}$ 및$$ $v{\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$ ${\$이$($가) $G{\displaystyle }$ ${\displaystyle G}$의 개별 구성 요소 정점인$$ 경우 $G{\displaystyle }$${\displaystyle v$$}$ 및 $v$ ${\displaystyle {\prime }^{}}$ ${\$을(가)에서 새 꼭지점 $v{\displaystyle }$ ${\$)로$$ 식별하여$$ 새 그래프 $G{\displaystyle {}^{}}$′ ${\$displaysteputepositions)을 생성할 수 있다.$G{\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$ ${\$의 $tyle {\textbf {v$$\}.$^[4] 더 일반적으로 정점 집합의 분할을 주어진 경우 파티션의 정점을 식별할 수 있으며, 결과 그래프를 몫 그래프라고 한다.

정점 절개

정점 분할과 동일한 정점 분할은 하나의 정점이 둘로 분할되고 있음을 의미하며, 여기서 이 두 개의 새로운 정점이 원래 정점이 인접한 정점에 인접해 있다.이것은 정점 식별의 역방향 조작이지만, 일반적으로 정점 식별의 경우, 확인된 정점 두 개의 인접 정점이 동일한 세트가 아니다.

경로 수축

경로 수축은 경로의 끝점 사이에 단일 가장자리를 형성하기 위해 수축되는 경로의 가장자리 집합에서 발생한다.경로를 따라 정점에 도달하는 가장자리는 제거되거나 엔드포인트 중 하나에 임의로(또는 체계적으로) 연결된다.

비틀기

Consider two disjoint graphs ${\displaystyle G_{1}}$ and ${\displaystyle G_{2}}$, where ${\displaystyle G_{1}}$ contains vertices ${\displaystyle u_{1}}$ and ${\displaystyle v_{1}}$ and ${\displaystyle G_{2}}$ contains vertices ${\displaystyle u_{2}}$and ${\displaystyle v_{2}}$. Suppose we can obtain the graph ${\displaystyle G}$ by identifying the vertices ${\displaystyle u_{1}}$ of ${\displaystyle G_{1}}$ and ${\displaystyle u_{2}}$ of ${\displaystyle G_{2}}$ as the vertex ${\displaystyle u}$ of ${\di$$splaystyle G}$ and identifying the vertices ${\displaystyle v_{1}}$ of ${\displaystyle G_{1}}$ and ${\displaystyle v_{2}}$ of ${\displaystyle G_{2}}$ as the vertex ${\displaystyle v}$ of ${\displaystyle G}$. In a twisting ${\displaystyle G'}$ of ${\displayst$정점 세트${\displaystyle }${${\displaystyle u,}$ ${\displaystyle v}$ ${\displaystyle \}}$ ${\displaystyle \{u,v$에 대해$$ $yle G}$을(를) 확인하고, $대신$ ${\displaystyle {u\mathrm{}}_{}}$ 1$${\$displaystyle u_{1},$ v ${\displaystyle {2\mathrm{}}_{}}$ ${\$$displaystyle$ $v_{$1}, u$$$$ $2{\displaystyle {}_{}}$ ${\$^[5]

적용들

가장자리 및 꼭지점 수축 기법 모두 그래프에서 정점 또는 가장자리 수에 대한 유도에 의해 입증에 가치가 있으며, 여기서 모든 작은 그래프에 대한 속성이 있다고 가정할 수 있으며 이는 더 큰 그래프에 대한 속성을 증명하는 데 사용될 수 있다.

모서리 수축은 임의로 연결된 그래프의 스패닝 트리 수에 대한 재귀 공식과 단순 그래프의 색다형 다항식의 반복 공식에 사용된다.^[6][7]

수축은 본질적으로 동등한 실체를 나타내는 정점을 식별하여 그래프를 단순화하려는 구조에서도 유용하다.가장 일반적인 예 중 하나는 강하게 연결된 각 구성 요소의 모든 정점을 수축하여 일반 방향 그래프를 반복 방향 그래프로 축소하는 것이다.그래프에서 설명한 관계가 전이적이라면, 우리가 각 정점에 그것을 형성하기 위해 수축된 정점의 라벨 세트를 라벨로 붙이는 한 어떤 정보도 손실되지 않는다.

또 다른 예는 고유 변수 간의 이동 작업을 제거하기 위해 정점이 수축되는 글로벌 그래프 컬러링 레지스터 할당에서 수행되는 병합이다.

가장자리 수축은 3D 모델링 패키지(수동으로 또는 모델링 소프트웨어의 일부 기능을 통해)에 사용되어 정점 수를 일관되게 감소시켜 저폴리곤 모델 생성에 도움이 된다.

참고 항목

• 하위분할(그래프 이론)

메모들

참조

• Gross, Jonathan; Yellen, Jay (1998), Graph Theory and its applications, CRC Press, ISBN 0-8493-3982-0
• Oxley, James (1992), Matroid Theory, Oxford University Press
• Rosen, Kenneth (2011), Discrete Mathematics and Its Applications (7th ed.), McGraw-Hill, ISBN 9780073383095
• West, Douglas B. (2001), Introduction to Graph Theory (2nd ed.), Prentice-Hall, ISBN 0-13-014400-2

외부 링크

• Weisstein, Eric W. "Edge Contraction". MathWorld.