중위수 그래프

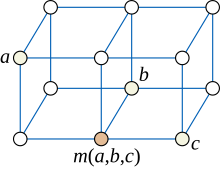
수학의 분할인 그래프 이론에서 중위수 그래프는 세 꼭지점 a, b, c마다 고유한 중위수를 갖는 비방향 그래프로, a, b, c의 각 쌍 사이의 최단 경로에 속하는 정점 m(a,b,c)이다.

중앙 그래프 개념은 오랫동안 연구되어 왔으며, 예를 들어 비르코프 & 키스(1947년)나 (더 명시적으로) 아반(1961년)에 의해 연구되어 왔으나, 이것을 "중간 그래프"라고 부르는 최초의 논문은 네베스크(1971년)로 보인다.정, 그레이엄, 삭스가 쓰듯이 "중간 그래프는 순서형 집합과 이산형 분배 격자 연구에 자연적으로 발생하며 방대한 문헌을 가지고 있다"^[1]고 한다.유전학에서, 모든 최대 파모니 진화 트리를 나타내는 Buneman 그래프는 중위수 그래프다.^[2]중위수 그래프는 사회적 선택 이론에서도 발생한다: 만약 대안의 집합이 중위수 그래프의 구조를 가지고 있다면, 그들 중 대다수의 선호도를 모호하지 않게 도출할 수 있다.^[3]

중앙 그래프에 대한 추가 조사는 클라바도르&멀더(1999년), 반델트&체포이(2008년), 크누스(2008년)가 제공한다.

예

모든 나무는 중앙 그래프다.^[4]이를 보려면, 나무에서 세 개의 꼭지점 a, b, c 쌍 사이의 세 개의 최단 경로의 결합 자체가 하나의 경로이거나, 세 개의 경로가 3등급의 단일 중앙 노드에서 만나면서 형성된 하위 트리임을 관찰한다.세 경로의 결합 자체가 하나의 경로인 경우, 중위수 m(a,b,c)은 a, b 또는 c 중 하나와 같으며, 이 세 가지 꼭지점 중 하나가 경로의 다른 두 가지 사이에 있다.3개의 경로의 결합에 의해 형성된 하위 트리가 경로가 아닌 경우, 3개의 꼭지점의 중위수는 하위 트리의 중심도 3 노드다.

중위수 그래프의 추가 예는 그리드 그래프에 의해 제공된다.격자 그래프에서 중위수 m(a,b,c)의 좌표는 a, b, c의 좌표의 중위수로 확인할 수 있다.반대로, 모든 중위수 그래프에서 중간값을 이러한 방식으로 좌표적으로 계산할 수 있는 방법으로 정수 격자의 점으로 정점을 표시할 수 있다.^[5]

사각형 그래프, 모든 내부 면이 4차선 측광선이고 모든 내부 정점이 4개 이상의 입사 모서리를 갖는 평면 그래프는 중위수 그래프의 또 다른 하위 등급이다.^[6]폴리오미노는 사각형 그래프의 특별한 경우여서 중앙 그래프도 형성한다.^[7]

임의의 비방향 그래프 G의 심플렉스 그래프 κ(G)은 G의 모든 클라이크(완전한 서브그래프)에 대한 정점을 가지고 있다; cl(G)의 두 정점은 해당 클릭이 G의 정점 하나만큼 다를 경우 에지로 연결된다. 심플렉스 그래프는 항상 중위수 그래프로서, 대부분의 규칙을 사용하여 주어진 세 개의 클릭의 중위수를 형성할 수 있다.포함할 클래스의 꼭지점 결정.^[8]

4개 이외의 길이의 사이클 그래프는 중위수 그래프일 수 없다.그러한 주기마다 세 개의 꼭지점 a, b, c가 있어 세 개의 최단 경로가 공통 교차점을 갖지 않고 사이클을 감싸고 있다.정점의 세 배에는 중위수가 있을 수 없다.

등가정의

임의 그래프에서, 각 두 꼭지점 a와 b에 대해, 그들 사이의 최소 에지 수를 d(x,y)로 나타내는 거리라고 한다.a와 b 사이의 최단 경로에 있는 정점의 간격은 다음과 같이 정의된다.

I(a,b) = {v d(a,b) = d(a,v) + d(v,b)}.

중위수 그래프는 세 꼭지점 a, b 및 c마다 이러한 구간이 단일 점에서 교차하는 속성으로 정의된다.

모든 a, b, c에 대해 I(a,b) ∩ I(a,c) ∩ I(b,c) = 1이다.

동등하게, a, b, c 3개의 꼭지점마다 그래프에서 가중치가 없는 거리가 등가치를 만족하는 정점 m(a,b,c)을 찾을 수 있다.

• d(a,b) = d(a,m(a,b,c) + d(a,b,c),b)
• d(a,c) = d(a,m(a,b,c) + d(a,b,c),c)
• d(b,c) = d(b,m(a,b,c) + d(a,b,c),c)

그리고 m(a,b,c)은 이것이 사실인 유일한 꼭지점이다.

또한 중앙값 그래프를 2-만족성 문제의 솔루션 집합으로 정의하고, 하이퍼큐브의 수축으로 정의하고, 유한한 중앙값 알헤브라의 그래프로 정의하고, 헬리 분할 시스템의 Bunman 그래프와 윈덱스 2의 그래프로 정의할 수도 있다. 아래 섹션을 참조하십시오.

분포 격자 및 중간 알헤브라스

격자 이론에서, 유한 격자 이론의 그래프는 각 격자 원소에 대한 정점과 격자의 피복 관계에 있는 각 요소 쌍에 대한 가장자리를 가지고 있다.격자는 일반적으로 하세 다이어그램을 통해 시각적으로 표시되는데, 이것은 격자의 그래프를 그린 그림이다.이 그래프들, 특히 분배 격자의 경우, 중위수 그래프와 밀접한 관계가 있는 것으로 나타났다.

분배 격자에서는 Birkhoff의 자체 이중 3차 중간 연산^[9]

m(a,b,c) = (a ∧ b) ∨ (a ∧ c) ∨ (b ∧ c) = (a ∨ b) ∧ (a ∨ c) ∧ (b ∨ c),

0부터 1까지의 범위에서 일반적인 수의 중위수 및 중위수 알헤브라와 더 일반적으로 공유하는 특정 핵심 공리를 만족한다.

• idempotence: $m{\displaystyle (a,}$a${\displaystyle ,}$ ${\displaystyle b}$ ) = 모든 a 및 b에 ${\displaystyle \mathrm{대한}}$ ${\displaystyle m(a,a,b)=a}$
• Commutativity: m(a, b, c)${\displaystyle =m(a,c,b)=m(b,a,c)=m(b,c,a)=m(c,a,b)=m(c,b,a)}$ for all a, b, and c.
• 분배도: $m{\displaystyle (,}$ ${\displaystyle m}$ (${\displaystyle b,}$ ${\displaystyle c,}$ ${\displaystyle d}$)${\displaystyle }$, ${\displaystyle e}$)${\displaystyle }$= ${\displaystyle m(,}$ ${\displaystyle b,}$ e${\displaystyle }$)${\displaystyle }$, ${\displaystyle c}$ ,${\displaystyle m}$ ${\displaystyle (,}$ $){\daystyle$ m $(a,m,c,d,e)=m(a,$b$,$e),$c,m(a,d,e$)}=m (a,d,e$)}}},$ e$$.
• ID 요소: m(0,a,1) = 모든 a에 대한 a.

분배법은 다음과 같은 연관법으로 대체될 수 있다.^[10]

• 연관성: m(x,w,m(y,w,z) = m(x,w,y),w,z)

중앙분리대 연산은 또한 분배 격차의 개념을 정의하는 데 사용될 수 있다.

I(a,b) = {x m(a,x,b) = x} = {x a ∧ b ≤ x ∨ a ∨ b}.^[11]

유한 분포 격자 그래프는 I(a,b) = {a,b}일 때마다 정점 a와 b 사이에 에지가 있다.이 그래프의 두 꼭지점 a와 b에 대해 위 격자-이론적 용어로 정의된 구간 I(a,b)는 a에서 b까지의 최단 경로에 있는 꼭지점으로 구성되며, 따라서 앞에서 정의한 그래프이론적 간격과 일치한다.3개의 격자 요소 a, b, c마다 m(a,b,c)은 3개의 구간 I(a,b), I(a,c), I(b,c)의 고유한 교차점이다.^[12]따라서 임의의 유한분산 격자의 그래프는 중위수 그래프다.Conversely, if a median graph G contains two vertices 0 and 1 such that every other vertex lies on a shortest path between the two (equivalently, m(0,a,1) = a for all a), then we may define a distributive lattice in which a ∧ b = m(a,0,b) and a ∨ b = m(a,1,b), and G will be the graph of this lattice.^[13]

Duffus & Relative(1983)는 분배 격자 그래프를 직경 보존형 하이퍼큐브의 수축으로 직접 특성화한다.보다 일반적으로 모든 중위수 그래프는 공차, 동시성 및 분배성을 만족하는 3차 연산을 발생시키지만, 분포 격자의 식별 요소는 없을 수 있다.이 세 가지 특성을 만족하는 유한 집합의 모든 3차 연산은 (그러나 반드시 0과 1 원소가 있는 것은 아님) 중위수 그래프와 같은 방식으로 상승한다.^[14]

볼록 세트와 헬리 패밀리

중위수 그래프에서 정점 집합 S는 S에 속하는 두 정점 a와 b마다 전체 구간 I(a,b)가 S의 부분 집합이면 볼록하다고 한다. 동등하게 위의 두 가지 구간에 대한 정의를 고려할 때, S는 정점 두 개 사이의 모든 최단 경로를 포함하거나 세 점 집합의 중위수를 포함하는 경우 볼록하다.그 중 적어도 두 개는 S에서 왔다.모든 볼록 세트 쌍의 교차점이 그 자체로 볼록한 것을 관찰한다.^[15]

중위수 그래프의 볼록 세트에는 헬리 특성이 있다. F가 임의의 쌍방향 교차 볼록 세트 제품군인 경우 F의 모든 세트에는 공통 교차점이 있다.^[16]왜냐하면, F가 쌍 S와 T, U의 교차점에 a, 쌍 T와 U의 교차점에 b, 그리고 쌍 S와 U의 교차점에 있는 볼록 세트 S, T, U를 3개만 가지고 있다면, a에서 b까지의 모든 최단 경로는 볼록도에 의해 T 안에 있어야 하며, 마찬가지로 다른 두 쌍의 꼭지점 사이의 모든 최단 경로는 반드시 위치해야 한다.나머지 두 세트를 얇게 한다. 그러나 m(a,b,c)은 세 쌍의 꼭지점 사이의 경로에 속하므로, 세 세트 모두 안에 있고, 공통 교차점의 일부를 형성한다.F에 볼록 세트가 3개 이상 있을 경우 결과는 세트 수에 따라 유도되며, 한 세트는 F의 임의 세트 쌍을 교차로에 의해 대체할 수 있으며, 세트의 세 쌍에 대한 결과를 사용하여 교체된 패밀리가 여전히 쌍으로 교차한다는 것을 보여줄 수 있다.

유클리드 공간의 반공간과 유사한 역할을 하는 중위수 그래프에서 특히 중요한 볼록 집합군이 집합이다.

W_uv = {w d(w,u) < d(w,v)}

그래프의 각 가장자리 UV에 대해 정의됨.즉 W는_uv v보다 u에 더 가까운 정점 또는 v에서 w까지의 어떤 최단 경로가 u를 통과하는 정점들로 구성된다.는 Wuv은 볼록을 보여 주기 위해서 w1w2자.고 Wuv 안에 끝 시작한다 Wk 자의적인 최단 경로, w2 또한 Wuv에서, 그렇지 않으면 이 둘점 m1하기 위한 m(u,w1,wk)그리고 m2가)m(m1,w2...Wk)u, w1,의(그 vertices 사이의 가능한 거리를 고려하여)에 뚜렷한 medians, 정중 g의 정의 모순적인 보여 줄 수 있중간계급이 유일해야 하는 랩.따라서 W의_uv 두 꼭지점 사이의 최단 경로에 있는 각각의 연속 정점 또한 W_uv 내에 있으므로 W는_uv 볼록성의 정의 중 하나인 노드 사이의 모든 최단 경로를 포함한다.

세트 W의_uv 헬리 속성은 아래 2-만족성 인스턴스(instance)의 솔루션으로서 중위수 그래프의 특성화에 핵심적인 역할을 한다.

2차원성

중위수 그래프는 이러한 그래프를 특성화하고 하이퍼큐브의 인접 보존 지도와 연관시키는 데 사용될 수 있는 2-만족성 문제의 솔루션 집합과 밀접한 관련이 있다.^[17]

2-만족도 인스턴스는 부울 변수의 집합과 절의 집합으로 구성되며, 이 두 변수가 특정 값의 조합을 피하도록 요구하는 특정 변수 쌍의 제약조건이다.일반적으로 그러한 문제들은 각 조항이 분리되어 표현되고 전체 제약조건 집합은 다음과 같은 조항들의 결합으로 표현되는 결합적 정상 형태로 표현된다.

${\displaystyle (x_{11}\lor x_{12})\land (x_{21}\lor x_{22}\land \cdots \land (x_{n1}\lor x_{n2})\land \cdots .}$

그러한 예에 대한 해결책은 모든 조항을 만족하는 변수에 대한 진실 값의 할당 또는 변수 값을 대체할 때 해당 예에 대한 결막 정규식 식을 참으로 만드는 동등하게 해당 예에 대한 진실 값의 할당이다.모든 해법의 집단은 중앙대수학으로서 자연구조를 가지고 있는데, 여기서 각 진리값을 세 해법에서 값의 과반수 함수로 선택함으로써 세 해법의 중위수가 형성된다. 이 중앙해법이 어떤 조항도 위반할 수 없다는 것을 쉽게 확인할 수 있다.따라서 이러한 용액은 중위수 그래프를 형성하는데, 이 그래프는 각 용액의 이웃이 서로 동일하거나 같지 않은 변수 집합을 모두 부정함으로써 형성된다.

반대로 모든 중위수 그래프 G는 2-만족성 인스턴스로 설정된 솔루션으로 이러한 방식으로 나타낼 수 있다.이러한 표현을 찾으려면 각 변수가 그래프에서 가장자리 중 하나의 방향을 설명하는 2-만족성 인스턴스(instance)를 생성하십시오(가장자리에 대한 방향 할당으로 그래프가 방향을 조정하지 않고 방향을 지정함). 각 제약조건은 두 가장자리가 있는 경우에만 한 쌍의 방향을 공유할 수 있도록 허용한다.텍스 v는 양쪽 방향을 따라 다른 vertices에서 G의 각 꼭지점 vv.에 짧은 길을 이 2-satisfiability 인스턴스에 모든 가장자리 대를 향한 인스턴스에 각각의 해결책이라는 꼭지점 v에서 가장자리를 잡은 세트가 Wuw의 여기서 v는 일반적인 교차로 이 방법으로 와야 하고 있는 해결 방법을 해당합니다.f롬 w to u; 이 공통 교차점은 집합 W의_uw 헬리 속성 때문에 존재한다.따라서 이 2-만족성 인스턴스(instance)에 대한 해결책은 G의 정점과 일대일로 대응한다.

하이퍼큐브 수축

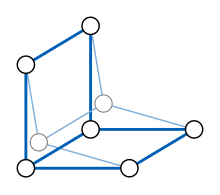
그래프 G의 수축은 G에서 그 하위 그래프 중 하나로 인접하게 보존되는 지도다.^[18]보다 정확하게는 서브그래프 φ(G)의 각 꼭지점 v에 대해 v(v) = v가 되도록 G에서 그 자체로 그래프 동형성 φ이다.수축의 이미지는 G의 수축이라고 불린다. 수축은 미터법 지도의 예로서, 모든 v와 w에 대해 φ(v)와 φ(w) 사이의 거리는 기껏해야 v와 w의 거리와 같으며, v와 w가 모두 g(G)에 속할 때마다 동일하다.따라서 수축은 G: 수축 거리의 등축 하위 그래프가 되어야 한다.

G가 중위수 그래프이고 a, b, c가 임의로 수축 φ(G)의 세 꼭지점이라면, ((a,b,c)는 a, b, c의 중위수여야 하며, 따라서 m(a,b,c)은 m(a,b,c)과 같아야 한다.따라서 φ(G)은 정점의 모든 세 곱에 대한 중위수를 포함하며, 또한 중위수 그래프여야 한다.즉, 중앙 그래프 패밀리는 수축 연산에 의해 닫힌다.^[19]

정점이 가능한 모든 k-비트 비트 벡터에 해당하고 해당 비트 벡터가 단 하나의 비트에서만 다를 때 두 정점이 인접한 하이퍼큐브 그래프는 k-차원 그리드 그래프의 특별한 경우로서, 따라서 중위수 그래프인 것이다.세 비트 벡터 a, b 및 c의 중간값은 각 비트 위치에서 a, b 및 c 비트의 다수 함수를 계산하여 계산할 수 있다.중앙 그래프들은 수축에 의해 닫히고, 하이퍼큐브를 포함하기 때문에, 하이퍼큐브의 모든 수축은 중앙 그래프다.

반대로 모든 중위수 그래프는 하이퍼큐브의 수축이어야 한다.^[20]이것은 위에서 설명한 중위수 그래프와 2만족도 사이의 연결에서 알 수 있다: G를 2만족도 사례에 대한 해결의 그래프가 되게 한다. 일반성의 손실 없이 이 사례는 모든 솔루션에서 두 변수가 항상 같거나 항상 같지 않은 방식으로 공식화될 수 있다.그러면 이 사례의 변수에 대한 모든 진실 할당 공간이 하이퍼큐브를 형성한다.두 변수의 분리 또는 그 보완으로 형성된 각 절에 대해, 2 만족도 사례에서, 이 절을 위반하는 진실 배정이 진실 배정의 다른 변수를 변경하지 않고 두 변수가 모두 해당 절을 만족시키는 진실 배정에 매핑되는 하이퍼큐브의 축소를 형성할 수 있다.각 절에 대해 이러한 방식으로 형성된 수축의 구성은 하이퍼큐브를 인스턴스의 솔루션 공간으로 수축시켜, 따라서 하이퍼큐브의 수축으로 G를 표현한다.특히 중위수 그래프는 하이퍼큐브의 등축 하위그래프여서 부분 큐브다.그러나 모든 부분 큐브가 중위수 그래프인 것은 아니다. 예를 들어 6Vertex 사이클 그래프는 부분 큐브이지만 중위수 그래프는 아니다.

Imrich & Klavzar(2000)에서 설명한 것처럼, 중앙값 그래프를 하이퍼큐브에 내장하는 등축은 시간 O(m log n)에 생성될 수 있으며, 여기서 n과 m은 각각 그래프의 정점과 가장자리 수입니다.^[21]

삼각형이 없는 그래프 및 인식 알고리즘

그래프가 중위수 그래프인지, 그리고 그래프가 삼각형이 없는지를 시험하는 문제들은 임리히, 클라바와 멀더(1999)가 어떤 의미에서 계산적으로 동등하다는 것을 관찰했을 때 잘 연구되었다.^[22]따라서 그래프가 삼각형이 없는지 여부를 테스트하기 위해 가장 잘 알려진 시간 범위인 O(m^1.41)^[23]는 그래프가 중위수 그래프인지 여부 테스트에도 적용되며 중위수 그래프 테스트 알고리즘이 개선되면 그래프에서 삼각형을 탐지하는 알고리즘도 개선될 수 있다.

한 방향에서 그래프 G를 입력하는 방식으로 G가 주어진다고 가정하고, G가 삼각형이 없는지를 테스트해야 한다.G에서 G의 0, 1 또는 2개의 인접 정점 세트의 정점으로 새 그래프 H를 생성한다.그러한 두 세트는 정확히 하나의 꼭지점만큼 차이가 날 때 H에 인접한다.H에 대한 동등한 설명은 G의 각 가장자리를 두 가장자리의 경로로 분할하고 G의 모든 원래 정점에 연결된 새로운 정점을 추가함으로써 형성된다는 것이다.This graph H is by construction a partial cube, but it is a median graph only when G is triangle-free: if a, b, and c form a triangle in G, then {a,b}, {a,c}, and {b,c} have no median in H, for such a median would have to correspond to the set {a,b,c}, but sets of three or more vertices of G do not form vertices in H.따라서 G는 H가 중위수 그래프인 경우에만 삼각형이 자유롭다.G가 삼각형이 없는 경우 H는 심플렉스 그래프다.이 구조에 의해 H가 중위수 그래프인지 여부를 효율적으로 테스트하기 위한 알고리즘도 G가 삼각형이 없는지를 테스트하는 데 사용된다.이 변환은 H의 크기가 G의 크기에 비례하기 때문에 문제의 계산 복잡성을 보존한다.

삼각형 검출에서 중위수 그래프 시험까지 다른 방향의 감소는 더 관여하며, 중위수 그래프에 필요한 여러 조건을 거의 선형에 가까운 시간에 시험하는 하가워, 임리치 & 클라브자르(1999)의 이전의 중위수 그래프 인식 알고리즘에 의존한다.새로운 핵심 단계는 폭의 첫 번째 검색을 사용하여 그래프의 정점을 임의로 선택한 루트 정점으로부터의 거리에 따라 그 수준으로 분할하고, 두 정점이 이전 수준에서 공통된 이웃을 공유하는 경우 인접한 각 수준에서 그래프를 형성하며, 이러한 그래프에서 삼각형을 검색하는 것을 포함한다.이러한 삼각형의 중위수는 세 개의 삼각형 꼭지점의 공통 이웃이어야 한다. 만약 이 공통 이웃이 존재하지 않는다면, 그래프는 중위수 그래프가 아니다.이러한 방법으로 발견된 모든 삼각형에는 중위수가 있고, 이전 알고리즘에서 그래프가 중위수 그래프에 대한 다른 모든 조건을 만족한다는 것을 발견하면, 실제로 중위수 그래프여야 한다.이 알고리즘은 삼각형이 존재하는지 여부를 테스트할 수 있는 기능뿐만 아니라 레벨 그래프의 모든 삼각형 목록을 요구한다.임의 그래프에서 모든 삼각형을 나열하는 데는 일부 그래프에는 많은 삼각형이 있기 때문에 Ω(m^3/2) 시간이 필요한 경우가 있지만, Hagauer 등은 그 감소의 수준 그래프에서 발생하는 삼각형의 수가 거의 선형에 가깝다는 것을 보여줌으로써, 사용할 삼각형을 찾기 위한 Alon 등 빠른 매트릭스 곱셈 기법을 사용할 수 있다.

진화 트리, Buneman 그래프 및 Hely 분할 시스템

계통생성은 종의 관찰된 특성으로부터 진화 나무를 추론하는 것이다. 그러한 나무는 종을 구별되는 정점에 배치해야 하며, 추가적인 정점을 가질 수 있지만, 잠재 정점은 세 개 이상의 입사 모서리를 가져야 하며 또한 특성으로 라벨을 붙여야 한다.특성은 2개의 가능한 값만 가지고 있을 때 이항이며, 종과 그들의 특성은 특정한 특성 값으로 표지가 된 정점(종과 잠재 정점)이 연속적인 하위 트리를 형성하는 진화 트리가 존재할 때 완벽한 계통 발생을 나타낸다.완벽한 계통생성을 가진 트리가 불가능할 경우, 트리 가장자리의 끝점이 모든 가장자리와 모든 특성에 대해 합쳐서 하나의 특성에 대해 서로 다른 값을 갖는 횟수를 최소화하면서, 최대 시차를 보이는 트리를 찾는 것이 종종 바람직하다.

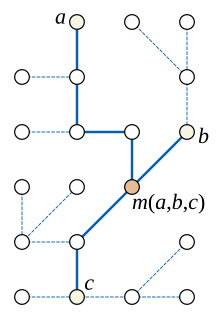
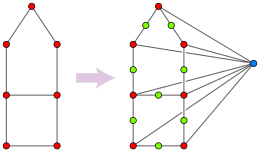
Buneman(1971)은 이항 특성에 대한 완벽한 계통생성을 유추하는 방법을 설명했다.그의 방법은 종과 이항 특성 집합에 대한 중위수 그래프의 구성으로 자연스럽게 일반화되는데, 이를 중위수 네트워크 또는 바이너리 그래프라고^[24] 하며 계통생성 네트워크의 일종이다.트리 가장자리가 그래프의 경로를 따르고 트리 가장자리의 특성 값 변화 횟수가 해당 경로의 숫자와 같다는 점에서 모든 최대 파모니 진화 트리가 바이먼 그래프에 내장된다.바이먼 그래프는 완벽한 계통생성이 존재하는 경우에만 트리가 될 것이다. 이는 네 가지 특성 값의 조합이 모두 관찰되는 두 가지 호환되지 않는 특성이 없을 때 발생한다.

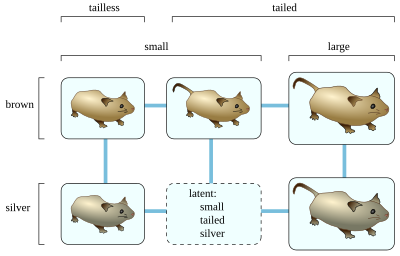
종과 특성의 집합에 대해 Buneman 그래프를 구성하려면 먼저 다른 종과 구별할 수 없는 중복성 종과 다른 특징과 항상 동일한 중복 특성을 제거한다.그런 다음 특성 값의 모든 조합에 대해 잠재 정점을 형성하여 어떤 알려진 종에 두 개의 값이 모두 존재하도록 한다.표시된 예에서 작은 갈색 미늘 없는 쥐, 작은 은색 미늘 없는 쥐, 작은 갈색 미늘이 있는 쥐, 큰 갈색 미늘이 있는 쥐, 큰 갈색 미늘이 있는 쥐, 큰 은색 미늘이 있는 쥐가 있다. 왜냐하면 모든 쌍쌍의 조합(작고 은색, 작고 작은 쥐)이 있기 때문이다.꼬리, 은, 꼬리)는 다른 알려진 종에서 관찰된다.그러나, 이 방법은 큰 갈색 미늘 없는 생쥐의 존재를 유추하지 않을 것이다. 왜냐하면 어떤 쥐도 크고 미늘 없는 특성을 가지고 있지 않다고 알려져 있기 때문이다.일단 잠복 정점이 결정되면, 단일 특성에서 다른 모든 종의 쌍이나 잠복 정점 사이에 가장자리를 형성한다.

이항 특성 집합을 분할 시스템으로 동등하게 설명할 수 있는데, 이는 각 집합의 상호보완 집합이 패밀리에 있다는 특성을 갖는 집합 집합의 집합이다.이 분할 시스템은 각각의 특성 값에 대해 세트가 있으며, 그 값을 가지는 종으로 구성되어 있다.잠복 정점을 포함하면 결과 분할 시스템은 헬리 특성을 가지며, 교차하는 모든 쌍은 공통 교차점을 가진다.어떤 의미에서 중앙분리대 그래프는 헬리 분할 시스템에서 유래한 것으로 특징지어진다: 중앙분리대 그래프의 각 가장자리 uv에 대해 정의된 쌍(W_uv, W_vu)은 헬리 분할 시스템을 형성하므로, 이 시스템에 Buneman 그래프 구조를 적용하면 잠복 정점이 필요하지 않고 결과는 시작 그래프와 동일할 것이다.^[25]

반델트 외 연구진(1995)과 반델트, 맥컬레이 & 리차드(2000)는 바네만 그래프의 단순화된 손 계산 기법을 설명하고, 이 구조를 이용해 인간의 유전적 관계를 시각화한다.

추가 속성

• 두 개의 중위수 그래프마다 데카르트 산물이 다른 중위수 그래프다.제품 그래프의 중위수는 그리드 그래프의 중위수가 각 선형 차원의 중위수를 독립적으로 찾아 계산되는 것처럼 두 요인에서 중위수를 독립적으로 찾아 계산하여 계산할 수 있다.
• 그래프의 윈덱스는 일련의 그래프 정점들이_i 주어지는 문제를 최적으로 해결하는 데 필요한 룩어헤드의 양을 측정하며, d(s_i, t_i)와 d(t_{i − 1}, t_i) 거리의 합을 최소화하는_i 또 다른 정점들을 출력할 때 찾아내야 한다.중위수 그래프는 정확히 윈덱스 2가 있는 그래프다.중위수 그래프에서 최적의 선택은 t_i = m(t_{i − 1i}, s, s_{i + 1})을 설정하는 것이다.^[1]
• 고유한 중위수를 갖는 속성을 고유한 스타이너 포인트 속성이라고도 한다.^[1]중위수 그래프에서 세 개의 꼭지점 a, b 및 c에 대한 최적 Steiner 트리는 a, b 및 c에서 m(a,b,c)까지의 세 개의 최단 경로의 결합으로 찾을 수 있다.Bandelt & Barthelémy(1984)는 주어진 정점 집합에 대한 거리의 합을 최소화하는 정점을 찾는 문제를 더 일반적으로 연구하며, 중위수 그래프에서 정점의 홀수 수에 대한 고유한 해결책을 가지고 있음을 보여준다.그들은 또한 중위수 그래프에서 정점의 집합 S의 중위수가 선거의 승자에 대한 콘도르셋 기준을 만족한다는 것을 보여준다. 다른 정점에 비해, 그것은 S에서 정점의 과반수에 가깝다.
• 일반적으로 부분 큐브와 마찬가지로, 정점이 n개인 모든 중위수 그래프에는 최대 (n/2)개의₂ 로그 가장자리가 있다.단, 가장자리 수는 너무 적을 수 없다: 클라브자르, 멀더 & 슈크레코프스키(1998)는 모든 중위수 그래프에서 2n - m - k k 2가 갖는 불평등도를 증명한다. 여기서 m은 가장자리 수, k는 그래프가 수축하는 하이퍼큐브의 치수다.이 불평등은 중위수 그래프에 큐브가 없는 경우에만 동등하다.이는 중위수 그래프에 대한 또 다른 정체성의 결과로서 오일러 특성 σ(-^dim(Q)1)은 항상 1과 같으며, 여기서 합은 주어진 중위수 그래프의 모든 하이퍼큐브 하위 그래프 Q를 차지한다.^[26]
• 유일한 정규 중위수 그래프는 하이퍼큐브다.^[27]
• 모든 중위수 그래프는 모듈형 그래프다.모듈형 그래프는 모든 꼭지점 세 개에 중위수가 있지만 중위수가 고유할 필요는 없는 그래프의 한 종류다.^[28]

메모들

참조

외부 링크

• 중위수 그래프, 그래프 클래스 포함에 대한 정보 시스템.
• 네트워크, 무료 Phylogenetic Network Software.네트워크는 유전, 언어, 그리고 다른 데이터로부터 진화 나무와 네트워크를 생성한다.
• PhilloMurka, 생물학적 데이터로부터 중앙분리대 네트워크 계산을 위한 오픈소스 소프트웨어.