토러스 매듭

매듭 이론에서, 토러스 매듭은 R에서³ 매듭을 짓지 않은 토러스 표면에 놓여 있는 특별한 종류의 매듭이다.마찬가지로, 토러스 링크는 토러스 표면에 같은 방식으로 놓여 있는 링크다.각 torus 매듭은 coprime 정수 p와 q의 쌍으로 지정된다. p와 q가 coprime이 아닌 경우 torus 링크는 gcd(p, q)이다.torus 매듭은 p 또는 q가 1 또는 -1인 경우에만 사소한(knot과 동일)이다.가장 간단한 비경쟁적인 예는 트레포일 매듭이라고도 알려진 (2,3)-토러스 매듭이다.

기하학적 표현

토러스 매듭은 지형학적으로 등가지만 기하학적으로 구별되는 여러 가지 방법으로 기하학적으로 렌더링될 수 있다(아래 속성 참조).이 글과 그 수치에 사용된 관례는 다음과 같다.

(p,q)-토러스 매듭은 토러스 내부의 원을 중심으로 q배, 회전 대칭 축을 중심으로 p배 감는다.{주, p와 q의 이러한 역할의 사용은 다음과 같은 것에 나타나는 것과 반대된다: http://mathworld.wolfram.com/TorusKnot.html 그것은 또한 아래 토러스 매듭의 "목록"과 그리고 "36 토러스 매듭"에 나타나는 그림과도 일치하지 않는다.} p와 q가 상대적으로 prime이 아니라면, 둘 이상의 구성요소를 가진 torus 링크가 있다.

매듭의 가닥이 토러스 둘레를 감싸는 방향도 서로 다른 관습에 따라 달라진다.가장 흔한 것은 가닥이 p q > 0을 위해 오른손 나사를 형성하도록 하는 것이다.^[1][2][3]

(p,q)-토러스 매듭은 파라메트리제이션에 의해 주어질 수 있다.

${\displaystyle {\phigrated}x&=r\cos(p\phi )\\y&=r\sin(p\phi )\\z&=\sin(q\phi )\ended}}}}$

where ${\displaystyle r=\cos(q\phi )+2}$ and ${\displaystyle 0<\phi <2\pi }$. This lies on the surface of the torus given by ${\displaystyle (r-2)^{2}+z^{2}=1}$ (in cylindrical coordinates).

매듭은 연속 변형까지 정의되기 때문에 다른 매개변수도 가능하다.The illustrations for the (2,3)- and (3,8)-torus knots can be obtained by taking ${\displaystyle r=\cos(q\phi )+4}$, and in the case of the (2,3)-torus knot by furthermore subtracting respectively ${\displaystyle 3\cos((p-q)\phi )}$ and ${\displaystyle 3\sin((p-$$q)\phi )}$을(를) x와 y의 위의 매개 변수에서 확인하십시오$$.후자는 어느 복사기 p,에나 원활하게 일반화된다. < 2 <\$displaystyle p<q<2p$

특성.

p 또는 q가 1 또는 -1이면 토러스 매듭은 사소한 것이다.^[2][3]

각각의 비종교적인 토러스 매듭은 프라임과^[4] 치랄이다.^[2]

(p,q) torus 매듭은 (q,p) torus 매듭과 동일하다.^[1][3]이것은 토러스 표면의 가닥을 움직이면 증명할 수 있다.^[5](p,-q) 토러스 매듭은 (p,q) 토러스 매듭의 반대(거울 이미지)이다.^[3](-p,-q) 토러스 매듭은 (p,q) 토러스 매듭과 동일하지만, 반대 방향은 제외한다.

모든 (p,q)-토러스 매듭은 p 가닥으로 닫힌 땋기로 만들 수 있다.적절한 땋은 말은

${\displaystyle (\displaystyle _{1}\cdma _{2}\cdots \cdots \cdma _{p-1}^{q}}}}}$

(이 공식은 ^[2][6][7][8]땋은 생성기는 우여곡절이라는 일반적인 관례를 가정하며, 땋은 머리 위에 위키피디아 페이지가 뒤따르지 않는다.)

p,q > 0과 a (p,q) torus 매듭의 교차 번호는 다음과 같다.

c = 최소(p-1)q, (q-1)p).

p,q > 0이 있는 토러스 매듭의 속은

${\displaystyle g={\frac {1}{2}}(p-1)(q-1).}$

토러스 매듭의 알렉산더 다항식은

${\displaystyle t^{k}{\frac {(t^{pq}-1)(t-1)}{(t^{p}-1)(t^{q}-1)}},}$ where ${\displaystyle k=-{\frac {(p-1)(q-1)}{2}}.$$}$

존스 다항식 토러스 매듭은 (우측)에 의해 주어진다.

${\displaystyle t^{(p-1)(q-1)/2}{\frac {1-t^{p+1}-t^{q+1}+t^{p+q}{1-t^{2}}.}$

3-sphere의 토러스 매듭의 보완재는 두 개의 단수 섬유로 디스크 위에서 섬유화된 세이퍼트-파이버 다지관이다.

내부에서 디스크가 제거된 p-폴드 던스 캡이 Y가 되고, 내부가 제거된 디스크가 있는 q-폴드 던스 캡이 Z가 되며, 경계 원을 따라 Y와 Z를 식별하여 얻은 지수 공간이 X가 된다.(p, q) -토러스 매듭 변형의 매듭보완은 공간 X로 수축한다.그러므로, 토러스 매듭의 매듭 그룹은 프레젠테이션을 한다.

${\displaystyle \langle x,y\mid x^{p}=y^{q}\angle .}$

토러스 매듭은 매듭 그룹의 중심부가 아닌 유일한 매듭(무한 주기, 위의 프레젠테이션에서$$ 원소 $x{\displaystyle {}^{}}$ ${\displaystyle p^{}}$= ${\displaystyle {}^{}}$ ${\displaystyle q^{}}$ ${\$이다.

유클리드 공간에서 곡선으로 (p,q) 토러스 매듭의 스트레치 계수는 Ω(min(p,q))이므로 토러스 매듭에는 무한 확장 계수가 있다.학부 연구원 존 사면은 미하일 그로모프가 원래 제기했던 문제를 해결한 이 결과를 증명하는 연구로 2012년 모건상을 수상했다.^[9][10]

복잡한 하이퍼러페이스에 연결

(p,q)-토러스 노트는 격리된 복합 초경면 특이점의 연결을 고려할 때 발생한다.하나는 복잡한 초저면을 초저엽과 교차하고, 고립된 단수점을 중심으로 하며, 다른 단수점을 둘러싸거나 마주치지 않도록 반경이 충분히 작다.교차로에서 하이퍼바이저의 서브매니폴드가 나온다.

p와 q는 2보다 크거나 같은 정수가 되도록 하라.Consider the holomorphic function ${\displaystyle f:\mathbb {C} ^{2}\to \mathbb {C} }$ given by ${\displaystyle f(w,z):=w^{p}+z^{q}.}$ Let ${\displaystyle V_{f}\subset \mathbb {C} ^{2}}$ be the set of ${\displaystyle (w,z)\in \ma$Thbb(^{2}}가 f(w, z)=0입니다.{\displaystyle f(w,z)=0.}진정한 숫자 0개체, ε ≪ 1을 감안할 때{0<, \varepsilon \ll 1\displaystyle,}우리는 ⊂ R4↪ C2{\displaystyle \mathbb{S}_{\varepsilon}^{3}\subset \mathbb{R}^{4}\hookrightarrow \mathbb{C}^{2}} 할 때three-sphere Sε 3정의한다.n에 의해${\displaystyle$$$ The function ${\displaystyle f}$ has an isolated critical point at ${\displaystyle (0,0)\in \mathbb {C} ^{2}}$ since ${\displaystyle \partial f/\partial w=\partial f/\partial z=0}$ if and only if ${\displaystyle w=z=0.}$$$ Thus, we consider the structure of ${\displaystyle V_{f}}$ close to ${\displaystyle (0,0)\in \mathbb {C} ^{2}.}$ In order to do this, we consider the intersection ${\displaystyle V_{f}\cap \mathbb {S} _{\varepsilon }^{3}\subset \mathbb {S} _{\varepsilon }^$${3}.}$ This intersection is the so-called link of the singularity ${\displaystyle f(w,z)=w^{p}+z^{q}.}$ The link of ${\displaystyle f(w,z)=w^{p}+z^{q}}$, where p and q are coprime, and both greater than or equal to two, is exactly the (p,q)−torus knot.^[11]

리스트

오른쪽의 그림은 토러스 링크(72,4)이다.

• Unknot, 3 매듭₁(3,2), 5₁ 매듭(5,2), 7₁ 매듭(7,2), 8₁₉ 매듭(4,3), 9₁ 매듭(9,2), 10₁₂₄ 매듭(5,3)

테이블 #	A-B	이미지	P	Q	십자형 #
0	01				0
3a1	31		3	2	3
5a2	51		5	2	5
7a7	71		7	2	7
8n3	819		4	3	8
9a41년	91		9	2	9
10n21년	10124		5	3	10
11a367년			11	2	11
13a4878			13	2	13
14n2188			7	3	14
15n41185		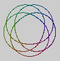	5	4	15
15a85263			15	2	15
16n783154			8	3	16
			17	2	17
			19	2	19
			10	3	20
			7	4	21
			21	2	21
			11	3	22
			23	2	23
			6	5	24
			25	2	25
			13	3	26
			9	4	27
			27	2	27
			7	5	28
			14	3	28
			29	2	29
			31	2	31
			8	5	32
			16	3	32
			11	4	33
			33	2	33
			17	3	34
			7	6	35
			35	2	35
			9	5	36
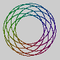			8	7	48
			9	7	54
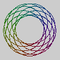			9	8	63

g-토러스 매듭

g-토러스 매듭은 g-토러스 위에 그려진 닫힌 곡선이다.좀 더 기술적으로 S³에서 g 핸들바디의 부분집합으로 실현될 수 있는 S³의 원의 동형상이다(그들의 보완물도 g 핸들바디 속이다).만약 링크가 2개의 핸들바디의 부분집합이라면, 그것은 이중토러스 링크다.^[12]

속 2의 경우, 토러스 매듭이 아닌 이중 토러스 매듭의 가장 간단한 예는 그림 8 매듭이다.^[13][14]

참고 항목

• 교대 매듭
• 위성 매듭
• 쌍곡 매듭
• 비합리적인 토러스 구불구불
• 토포폴리스

참조

외부 링크

• "36 토러스 노츠" 매듭 아틀라스
• Weisstein, Eric W. "Torus Knot". MathWorld.
• 액션스크립트의 토러스 매듭 렌더러
• PQ-Torus 매듭으로 재미있다