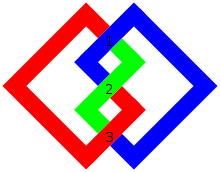
교차수(노트가론)

Crossing number (knot theory)
교차로 라벨이 부착된 3중 대칭이 없는 3중 날개 매듭.
교차 번호가 7개 이하인 모든 프라임 노트 표(미러 이미지 제외).

매듭 이론의 수학적 영역에서, 매듭의 교차 수는 매듭의 도표 중 가장 작은 수의 교차입니다.매듭 불변량이다.

예

예를 들어, 언노트에는 교차번호 0, 삼엽매듭 3 및 그림 8매듭 4가 있습니다.건널목 수가 이렇게 적은 노트는 없고, 건널목 수가 5번인 노트는 2개뿐이지만 건널목 수가 늘어날수록 건널목 수가 급증한다.

표

소수 매듭의 표는 전통적으로 교차 번호에 의해 색인화되며, 이렇게 많은 교차 매듭 중 어떤 특정 매듭이 의미되는지 나타내는 첨자가 붙습니다(이 하위 순서는 토러스 매듭과 트위스트 매듭이 먼저 나열되는 것을 제외하고 특별히 아무 것도 기초로 하지 않습니다).리스트에는 3(트리포일 매듭), 41(그림8 매듭), 51, 521, 6 등이 있습니다1.이 순서는 1877년 [1]P. G. Tait가 매듭 표를 발표한 이후 크게 변하지 않았다.

가감성

정사각형 매듭(cr(6) = 삼엽상(cr(3)) + 삼엽상 반사(cr(3)).

매듭에 대한 기본적인 작업 하에서 숫자를 건너는 행동을 이해하는 데 있어 거의 진전이 없었다.매듭 합계를 계산할 때 교차 번호가 가법적인지 여부를 묻는 큰 개방형 질문이 있습니다.또한 매듭 K의 위성은 K보다 교차수가 클 것으로 예상되지만 이는 증명되지 않았다.

예를 들어, 섬이 교대 매듭[2](또는 더 일반적으로 적절한 매듭)이거나 섬이 토러스 [3][4]매듭인 경우 등 특수한 경우에 대해 매듭 합 아래의 교차 숫자의 가산성이 입증되었다.Marc Lackenby는 또한 (1) + ( 2)( c ( 2) \ { } { } ( \ textstyle { ( K _ { 1 ) + \ { } ( K { 1 ) + { K） 1 N c 1 N 、 、 、 、 > 1 1 N 。

생물정보학에서의 응용

매듭의 교차수와 DNA 매듭의 물리적 행동 사이에는 연관성이 있다.주요 DNA 매듭의 경우 교차수는 아가로스 겔 전기영동에서의 DNA 매듭의 상대 속도를 예측하는 좋은 예측 변수이다.기본적으로 건널목 수가 높을수록 상대 속도가 빨라집니다.복합 매듭의 경우 실험 조건에 [6]따라 결과가 크게 달라질 수 있지만 그렇지 않은 것으로 보인다.

관련 불변량

평균 교차 수와 점근 교차 수의 관련 개념이 있습니다.이 두 수량은 모두 표준 교차 번호에 묶였다.점근교차수는 교차수와 동일한 것으로 추측된다.

기타 숫자 매듭 불변수에는 브리지 번호, 링크 번호, 스틱 번호 및 노트 해제 번호가 포함됩니다.

레퍼런스

  1. ^ 를 클릭합니다Tait, P. G. (1898), "On Knots I,II,III'", Scientific papers, vol. 1, Cambridge University Press, pp. 273–347.
  2. ^ 를 클릭합니다Adams, Colin C. (2004), The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots, Providence, RI: American Mathematical Society, p. 69, ISBN 9780821836781, MR 2079925.
  3. ^ 를 클릭합니다Gruber, H. (2003), Estimates for the minimal crossing number, arXiv:math/0303273, Bibcode:2003math......3273G.
  4. ^ 를 클릭합니다Diao, Yuanan (2004), "The additivity of crossing numbers", Journal of Knot Theory and its Ramifications, 13 (7): 857–866, doi:10.1142/S0218216504003524, MR 2101230.
  5. ^ 를 클릭합니다Lackenby, Marc (2009), "The crossing number of composite knots", Journal of Topology, 2 (4): 747–768, arXiv:0805.4706, doi:10.1112/jtopol/jtp028, MR 2574742.
  6. ^ 를 클릭합니다Simon, Jonathan (1996), "Energy functions for knots: Beginning to predict physical behavior", in Mesirov, Jill P.; Schulten, Klaus; Sumners, De Witt (eds.), Mathematical Approaches to Biomolecular Structure and Dynamics, The IMA Volumes in Mathematics and its Applications, vol. 82, pp. 39–58, doi:10.1007/978-1-4612-4066-2_4.