사냐크 효과

그림 1Sagnac 간섭계의 개략도.

프랑스 물리학자 조르주 사냐크의 이름을 딴 사냐크 간섭이라고도 불리는 사냐크 효과는 회전에 의해 유도되는 간섭계에서 마주치는 현상이다.Sagnac 효과는 링 간섭계 또는 Sagnac 간섭계라고 불리는 설정에서 나타납니다.빛의 빔이 분할되어 두 빔이 같은 경로를 따르지만 반대 방향으로 흐른다.진입점으로 돌아가면 두 개의 광선이 링에서 나와 간섭을 받습니다.두 개의 기존 빔의 상대 위상 및 간섭 가장자리의 위치는 장치의 각 속도에 따라 이동합니다.즉, 간섭계가 비회전 프레임에 대해 정지해 있을 때는 어느 방향으로든 링을 통과하는 데 같은 시간이 걸린다.그러나 간섭계 시스템이 회전할 때 기계 프레임의 한 회로를 완성하기 위해 한쪽 빔이 다른 쪽 빔보다 이동하는 경로가 길기 때문에 시간이 오래 걸리기 때문에 두 빔의 위상차가 발생한다.조르주 사냐크는 아인슈타인의 특수 상대성 이론이 ^[1]^[2]버린 에테르의 존재를 증명하기 위해 이 실험을 설정했다.

짐벌에 장착된 기계식 자이로스코프는 회전 업 후에도 동일한 방향을 가리키고 있으므로 관성 항법 시스템의 회전 기준으로 사용할 수 있습니다.Sagnac 효과에 기초한 레이저 자이로스코프와 광섬유 자이로스코프의 개발로, 부피가 큰 기계 자이로스코프는 많은 현대 관성 항법 시스템에서 움직이는 부품이 없는 것으로 대체될 수 있습니다.기존의 자이로스코프는 각운동량 보존 원리에 의존하는 반면, 링 간섭계의 회전 감도는 모든 관성 기준 프레임에 대한 빛의 속도의 불변성에서 발생한다.

설명 및 조작

그림 2유도파 Sagnac 간섭계, 즉 광섬유 자이로스코프는 1개 또는 복수의 루프에서 광섬유를 사용하여 실현할 수 있다.

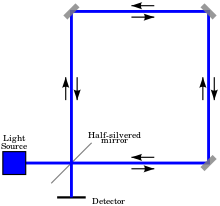
일반적으로 3개 이상의 거울이 사용되므로 역전파광 빔이 삼각형이나 정사각형과 같은 닫힌 경로를 따르도록 한다(그림 1).또는 광섬유를 사용하여 닫힌 경로를 통해 빛을 유도할 수 있습니다(그림 2).링 간섭계가 탑재된 플랫폼이 회전하고 있는 경우에는 플랫폼이 회전하고 있지 않을 때 간섭 테두리가 그 위치에 비해 변위한다.변위량은 회전 플랫폼의 각 속도에 비례합니다.회전축은 밀폐된 영역 내에 있을 필요가 없습니다.간섭 프링의 위상 편이는 플랫폼의 각 주파수 ${\boldsymbol {\omega }}$ (\ $displaystyle\boldsymbol\mega}})$ 에 ${\boldsymbol {\omega }}$ 비례하며, Sagnac에 의해 최초로 도출된 공식에 따라 결정됩니다.

\displaystyle \Delta \phi \약 \frac {8\pi }{\lambda c}}{\boldsymbol \mega }}\cdot \mathbf {A}}

\mathbf {A}

서

\mathbf {A}

\

displaystyle \mathbf {A}

는

\mathbf {A}

루프의 방향 영역이고

\displaystyle \lambda는

빛의

\lambda

파장입니다.

이 효과는 간섭계 링에서 전체 라운드 트립을 완료하는 데 좌우 이동 광선이 걸리는 시간이 서로 다르기 때문입니다.이동시간의 차이에 $c/\lambda$ c / ${\$ ( \ $displaystyle$ c / \ $lambda$ 를 곱하면 $\Delta \phi$ ${\$ ( \ $displaystyle$ \ $Delta$ \ $phi$ 가 결정됩니다.

따라서 측정된 회전은 절대 회전, 즉 관성 기준 프레임에 대한 플랫폼의 회전입니다.

역사

1887년의 Michelson-Morley 실험은 가상의 발광 에테르가 존재한다면, 지구에 의해 완전히 끌려갔다는 것을 시사했다.이 가설을 시험하기 위해 1897년 올리버 로지는 지구의 자전을 측정하기 위해 거대한 고리 간섭계를 만들 것을 제안했다; 1904년 Albert Abraham Michelson에 의해 비슷한 제안이 있었다.그들은 그러한 간섭계로, 지구에 의해 부분적으로 또는 완전히 끌려가는 에테르와 정지된 에테르 사이에서 결정하는 것이 가능하기를 희망했다.즉, 가상의 에테르를 지구(또는 간섭계)에 의해 운반한다면 결과는 음이 되는 반면, 정지 상태의 에테르에는 양의 ^[3]^[4]^[5]결과가 나온다.

움직이는 유리를 통해 전파되는 빛의 플레넬 항력을 측정하기 위해 1911년 프란츠 해러스에 의해 수행된 실험은 1920년 막스 폰 라우에에에 의해 실제로 Sagnac 실험을 구성하는 것으로 인정되었습니다.Sagnac 효과를 몰랐던 Harress는 그의 측정에서 "예상치 못한 편견"의 존재를 깨달았으나 ^[6]그 원인을 설명할 수 없었다.

특수 상대성 이론의 틀에서 사냐크 효과에 대한 첫 번째 설명은 사냐크가 실험을 하기 2년 전인 ^[7]^[8]1911년에 라우에에에 의해 이루어졌다.Michelson(1904)의 이론적 작업을 계속함으로써, von Laue는 관성 기준 프레임("유효한" 기준 프레임이라고 함)에 자신을 제한했고, 각주에 "유효한 $K^{0}$ K $(\$ K $^{0})$ 에 $K^{0}$ 대해 회전하는 시스템은 유효하지 않습니다."^[7]라고 썼다. $광속$ c {\ $displaystyle$ c $c$ 를 일정 광속 $\omega$ c {\ $displaystyle \obega$ 로 설정하고, 1개의 광선의 전파시간 $\tau _{+}$ $+\$ _ ${+}$ 와 $\tau _{+}$ 역전파선의 $\tau _{-}$ - $\tau _{-}$ \ $displaystyle \tau$ _ ${-}$ 를 $\tau _{-}$ 계산하여 시차 $\Delta \tau =\tau _{+}-\tau _{-}$ 를 구했다. $\Delta \tau =\tau _{+}-\tau _{-}$ = $-$ + $\Delta \tau =\tau _{+}-\tau _{-}$ - $\Delta \tau =\tau _{+}-\tau _{-}$ - τ - \ $displaystyle$ \ $Delta$ \ delta = \ $delta$ _ { + $}$ - \ $delta$ _ { $\Delta \tau =\tau _{+}-\tau _{-}$ - }. 그는 이 간섭계 실험이 $v/c$ 상대성 이론과 정적 에테르(후자 "절대 r" 이론에서 "style $v/c$ 의 $v/c$ 항으로 제한될 때 동일한 양의 결과를 낼 것이라고 결론지었다.1895년 로렌츠 이론에 대한 언급).그는 또한 (스토크스나 헤르츠 같은) 완전한 에테르 드래그 모델만이 부정적인 ^[7]결과를 가져올 것이라고 결론지었다.

실제로, 각속도와 위상 편이의 상관관계를 관찰하기 위한 최초의 간섭계 실험은 1913년 프랑스 과학자 조르주 사냐크에 의해 수행되었다.이것의 목적은 "에테르 상대적 운동의 영향"^[1]^[2]을 감지하는 것이었다.Sagnac은 그의 결과가 정지 에테르 존재의 증거라고 믿었다.하지만, 위에서 설명한 것처럼, 막스 폰 라우에는 이미 1911년에 이 효과가 특수 상대성 ^[7]^[8]이론과 일치한다는 것을 보여주었다.지구 항력에 의해 발생하는 에테르 바람을 증명하기 위해 조심스럽게 준비된 Michelson-Morley 실험과는 달리, Sagnac 실험은 회전하는 빛의 모든 부분에 동일하게 영향을 미치기 때문에 이러한 유형의 에테르 바람을 증명할 수 없었다.

아인슈타인은 1914년 ^[9]폴 하저가 쓴 "유리와 수차의 빛 끌기"라는 기사에서 수학적으로 분석한 프란츠 해러스의 초기 실험을 통해 사냐크 효과의 현상을 완전히 인지했다.이것은 아인슈타인에 의해 그의 기사 "Observation on P"에서 반박되었다.Harzer의 기사: 유리와 ^[10]수차의 빛의 질질 끌기와 P에 대한 답변.하저의 회답"^[11]아인슈타인의 수학적 주장이 첫 번째 기사에서 나온 후, 아인슈타인은 "내가 보여 준 바와 같이, 빛의 주파수는 매체에 대한 빛의 속도를 결정하기 때문에 매그니튜드 k에 대해 결정적이다.이 경우 회전하는 프리즘 계통과 관련하여 정지 과정으로 이해해야 하는 가벼운 과정이다.따라서 움직이는 프리즘에 대한 빛의 주파수와 규모 k는 모든 프리즘에 대해 동일하다.이것은 Harzer씨의 답변을 부정합니다."(1914년)

1920년 폰 라우에는 해리스 실험을 기술하고 이 ^[6]실험에서 사냐크 효과의 역할을 보여주며 1911년 자신의 이론적 연구를 계속했다.Laue는 (빛이 유리를 가로지르는) Harress 실험에서 빛의 끌림(이동 매체의 상대론적 속도 추가에 따른)과 "회전 장치의 모든 부분이 O에 접근하는 동안 하나의 광선으로부터 멀어진다는 사실 둘 다로 인해 계산 가능한 시간 차이가 있었다"고 말했다.즉, Sagnac 효과입니다.그는 후자의 효과만으로는 시간 편차를 일으킬 수 있으며, 따라서 "자전에 연결된 가속도는 ^[6]빛의 속도에 영향을 미치지 않는다"고 인정했다.

Laue의 설명은 관성 프레임에 기초하고 있지만, Paul Langevin(1921, 1937)과 다른 사람들은 회전 기준 프레임에서 볼 때 같은 효과를 설명했다(특수 상대성 이론과 일반 상대성 이론 모두에서 Born 좌표 참조).따라서 Sagnac 효과를 코로테이션 프레임의 관점에서 설명해야 할 경우, 일반 회전 원통 좌표를 사용하여 민코프스키 메트릭에 적용할 수 있으며, 이는 이른바 Born 메트릭 또는 Langevin ^[12]^[13]^[14]메트릭으로 귀결됩니다.이러한 좌표로부터 역전파선의 다른 도달 시간을 도출할 수 있는데, 이 효과는 Paul Langevin(1921)^[15]에 의해 나타났다.또는 이들 좌표를 사용하여 회전하는 프레임에서 빛의 글로벌 속도를 계산하면 방향성에 따라 다른 외관광속도가 도출되며, 이 효과는 다른 논문(1937년)^[16]에서 Langevin에 의해 제시되었다.

이것은 특수 상대성 이론과 빛의 속도가 가속에 의해 영향을 받지 않는다는 von Laue의 위의 설명과 모순되지 않는다.회전하는 프레임에서 이 겉으로 보이는 가변 광속은 회전 좌표를 사용하는 경우에만 발생하는 반면, Sagnac 효과가 외부 관성 좌표 프레임의 관점에서 설명되는 경우 빛의 속도는 물론 일정하게 유지되기 때문에, Sagnac 효과는 관성 좌표를 사용하는지 여부에 관계없이 발생한다(공식 참조).(아래의 이론) 또는 회전 좌표 (아래의 § 참조 프레임의 공식 참조).즉, 원래 공식의 특수 상대성이론은 회전 프레임이 아닌 관성 좌표 프레임에 적용되었다.알버트 아인슈타인은 특수상대성이론을 소개하는 논문에서 "빛은 항상 방출하는 ^[17]물체의 운동 상태와 무관한 일정한 속도 c로 빈 공간에서 전파된다"고 말했다.아인슈타인은 광속은 빈 공간의 진공에서만 일정하다고 구체적으로 언급했는데, 이는 선형 및 평행 관성 프레임에서만 유지되는 방정식을 사용했다.하지만 아인슈타인이 가속 기준 프레임을 조사하기 시작했을 때,^[18] 그는 가속 기준 프레임을 위해 "빛의 항상성의 원리는 수정되어야 한다"는 것을 알아차렸다.

막스 폰 라우에(Max von Laue)는 1920년 논문에서 일반상대성이 사냐크 효과에 미치는 영향에 대해 진지하게 고려했다. "일반상대성이론은 당연히 그것에 대해 몇 가지 진술을 할 수 있을 것이고, 우리는 처음에 그것에 따라 가속의 눈에 띄는 영향이 예상되지 않는다는 것을 보여주고 싶다."그는 독일 물리학자 빌헬름 ^[6]빈과의 토론에 관한 각주를 작성한다.일반상대성이론을 보는 이유는 아인슈타인의 일반상대성이론이 빛이 중력장에서 느려질 것이라고 예측했기 때문에 거대한 물체 주변의 빛의 곡률을 예측할 수 있었기 때문이다.일반상대성 아래에는 중력과 가속도가 동등하다는 등가원리가 있다.간섭계를 회전시키거나 가속시키면 중력 효과가 발생한다."그러나 이러한 [비관성] 운동에는 두 가지 다른 유형이 있습니다. 예를 들어 직선의 가속이나 일정한 속도를 ^[19]가진 원형 운동입니다."또한, 1964년 어윈 샤피로는 "빛 파동의 속도는 그 경로를 따라 있는 중력 전위의 강도에 달려있다"고 일반 상대성 이론을 설명했다.이를 샤피로 ^[20]지연이라고 합니다.그러나 중력장이 중요해야 하기 때문에,^[6] Laue(1920)는 그 효과가 공간을 통한 이동에 의해 경로의 거리를 변화시킨 결과일 가능성이 더 높다고 결론지었다."회전 방향으로 루프 주위를 이동하는 빔은 회전 방향과 반대 방향으로 이동하는 빔보다 더 멀리 갈 것입니다. 왜냐하면 이동 기간 동안 거울과 검출기는 모두 역회전 빔을 향해 (약간) 이동하기 때문입니다.따라서 빔은 약간 다른 시간에 검출기에 도달하고 약간 위상이 어긋나 관찰 및 ^[21]측정이 가능한 광학 간섭 '프링'을 생성합니다."

1926년 앨버트 미셸슨과 헨리 게일에 의해 야심찬 고리 간섭계 실험이 시작되었다.그 목적은 지구의 자전이 지구 근처의 빛의 전파에 영향을 미치는지를 알아내는 것이었다.마이클슨-게일-피어슨 실험은 지구의 각속도를 감지할 수 있을 만큼 충분히 큰 고리 간섭계(둘레 1.9km)였다.실험 결과는 천문학으로 측정한 지구의 각속도가 측정 정확도 이내로 확인되었습니다.Michelson-Gale 실험의 링 간섭계는 외부 기준과 비교하여 보정되지 않았다(설정이 지구에 고정되어 있었기 때문에 가능하지 않았다).시프트가 제로일 경우 중앙 간섭 가장자리가 어디에 있어야 하는지 설계에서 추론할 수 있다.측정된 시프트는 1000분의 230 부품이었고 정확도는 1000분의 5 부품이었습니다.예측된 이동량은 ^[22]1000분의 237이었습니다.

Sagnac 효과는 그것의 의미와 ^[23]^[24]^[25]해석에 대한 한 세기 동안의 논쟁을 자극했고, 이 논쟁의 대부분은 특수 상대성 이론의 맥락에서 그 효과가 완벽하게 잘 이해되기 때문에 놀랍습니다.

이론.

기본 케이스

그림 3반대 방향으로 이동하는 빛은 이동원에 도달하기 전에 서로 다른 거리를 이동합니다.

링 간섭계의 간섭 테두리 변화는 링의 회전에 의해 빛이 이동하는 다른 거리의 결과로 직관적으로 볼 수 있습니다.(그림3)^[26] 굴절률 1인 반지름 R의 원형 링이 각속도 $\omega$ (\ $displaystyle\obega$ 로 회전하는 것이 가장 간단한 유도 방법이지만, 그 결과는 다른 형상의 루프 기하학이 일반적이다.광원이 회전링의 한 지점에서 양방향으로 방출되는 경우 회전방향과 같은 방향으로 이동하는 빛은 링 주위를 둘레 이상 이동한 후 뒤에서 광원을 따라잡아야 합니다.광원을 따라잡는 데 걸리는 $t_{1}$ $t_{1}$ 1 $({$ 1})은 $t_{1}$ 다음과 같습니다.

t_{1}=pi R+\Delta L}{c}

$L \displaystyle$ \ $Delta$ L은 $\Delta L$ 거울이 동시에 이동한 거리(그림 3의 검은색 굵은 화살표):

\displaystyle \Delta L=R\omega t_{1},

위의 두 공식에서 $\Delta L$ L $(\style\delta$ L $)$ 을 $\Delta L$ 제거하면 다음과 같이 됩니다.

t_{1}=black {2\pi R}{c-R\omega}}.

마찬가지로 회전의 반대 방향으로 이동하는 빛은 전면의 광원에 닿기 전에 원주 1개 이하로 이동합니다.따라서 이 빛의 방향이 다시 이동원에 도달하는 시간은 다음과 같습니다.

t_{2}=black {2\pi R}{c+R\omega}}.

시차가...

(\displaystyle \Delta t=t_{1}-t_{2}=black {4\pi R^{2}\obe }{c^{2}-R^{2}\obe ^{2}}).}

R $R\omega =v\ll c$ $R\omega =v\ll c$ $R\omega =v\ll c$ \ $displaystyle R$ \ omega $= v$ \ $ll$ c $R\omega =v\ll c$ }의 경우 이 값은 다음과 같습니다.

\Delta t\약 {frac {4\pi R^{2}\mega }{c^{2}} = flac {4}A\mega }{c^{2}}},

여기서 A는 링의 영역입니다.

그림 4Sagnac 영역 공식은 모든 루프 모양에 적용됩니다.

이 단순한 파생은 굴절률이 1인 원형 링에 대한 것이지만, 결과는 영역 A를 가진 회전 루프의 모든 형태에 적용된다(그림 4).

보다 복잡한 형태 또는 다른 굴절률 값은 페르마의 원리를 사용하여 각 방향의 광학 위상 편이를 계산하고 상대론적 광고를 사용하여 계산할 수 있는 관성 실험실 프레임의 다른 전파 방향에 대한 다른 위상 속도를 고려함으로써 동일한 결과를 도출할 수 있다.속도 ^[27]변화

광원에 배치된 테두리를 보기 위한 화면을 상상합니다(또는 빔슬리터를 사용하여 소스 포인트에서 화면으로 빛을 보냅니다).안정된 광원이 주어지면, 간섭 테두리는 두 개의 역회전 빔이 회로를 통과하는 데 필요한 시간 차이에 비례하는 프린지 변위를 가진 스크린에 형성됩니다.위상 시프트는 $\Delta \phi ={\frac {2\pi c\,\Delta t}{\lambda }}$ $\Delta \phi ={\frac {2\pi c\,\Delta t}{\lambda }}$ $\Delta \phi ={\frac {2\pi c\,\Delta t}{\lambda }}$ 2 $\Delta \phi ={\frac {2\pi c\,\Delta t}{\lambda }}$ c $\Delta \phi ={\frac {2\pi c\,\Delta t}{\lambda }}$ t $\Delta \phi ={\frac {2\pi c\,\Delta t}{\lambda }}$ { $displaystyle$ \ $Delta$ \ $phi$ = $fr$ frac ${ 2$ \ $pi$ c , \ $Delta$ t } $\Delta \phi ={\frac {2\pi c\,\Delta t}{\lambda }}$ { \ $delta$ t $}$ 입니다.이것에 의해 프링의 시프트는 A{\ $displaystyle$ A $}$ 및 $A$ \ $displaystyle }$ 에 $A$ 합니다.

비상대적 속도에서 Sagnac 효과는 광속의 원천 독립성의 단순한 결과이다.다시 말해, Sagnac 실험은 상대성 이전의 물리학과 상대성 ^[26]물리학을 구별하지 않는다.

광섬유 케이블로 빛이 전파될 때 설정은 Sagnac 실험과 Fizeau 실험의 효과적인 조합입니다.유리는 진공보다 빛의 속도가 느리고 광케이블은 움직이는 매체입니다.이 경우 상대론적 속도 가산 규칙이 적용됩니다.빛의 전파에 대한 상대주의 이전의 이론은 피조 효과를 설명할 수 없다. (1900년까지 로렌츠는 피조 효과를 설명할 수 있었지만, 그 무렵에는 그의 이론은 수학적으로 특수 상대성과 동등한 형태로 진화했다.)

이미터와 검출기는 같은 속도로 이동하기 때문에 도플러 효과는 상쇄되므로 Sagnac 효과는 도플러 효과를 수반하지 않는다.링 레이저 간섭법의 경우, 이 점에 유의하는 것이 중요합니다.링 레이저 설정이 회전하고 있을 때 역전파 빔은 반대 방향으로 주파수 이동을 거칩니다.이 주파수 이동은 도플러 이동이 아니라 링 레이저에서 설명하듯이 광학 공동 공명 효과입니다.

Sagnac 효과는 특수 상대성 이론의 맥락에서 잘 이해되며, 회전 광원의 관점에서 위상 차이는 시공간에서 ^[28]닫힌 루프를 형성하지 않는 광로를 따라 동시 라인에 기인한다.

일반화 공식

그림 5개념적으로 왼쪽의 기존 광섬유 자이로(FOG)는 오른쪽의 광섬유 컨베이어(FOC)와 같이 끝부분을 연결하는 연장 파이버가 있는 두 개의 반원형 섹션으로 분할되어 광섬유 컨베이어(FOC)를 생성할 수 있습니다.

광원이 (꼭 원형이 아닌) 광로를 따라 이동할 수 있도록 하여 실험의 수정된 버전이 제안되었다^[29].이 설정에서는 위상차이의 또 다른 원인이 생깁니다.광원에 따르면 2개의 신호가 공간 내에서 서로 다른 경로를 따릅니다.일부 저자는 이 효과를 Sagnac^[25]^[30] 효과라고 부르지만, 이 경우 폐루프를 형성하지 않는 동시 라인으로 인해 차이가 발생할 필요는 없다.

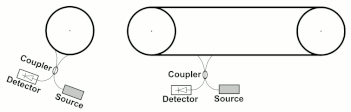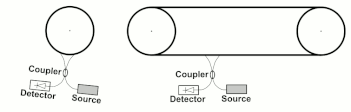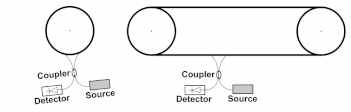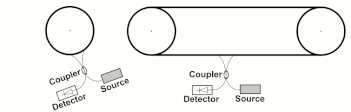
그림 5에 변경된 구성의 예가 나와 있는데, 왼쪽의 표준 광섬유 자이로스코프와 오른쪽의 광섬유 컨베이어에서 측정된 위상차는 빛의 일정한 속도에 기초하여 도출되는 δt = 2vL/c² 공식에 부합한다.이 공식에서 총 시간 지연은 파이버가 컨베이어의 회전 부분 또는 직선 부분에 있든 상관없이 파이버의 전체 길이를 따라 누적 시간 지연과 동일하다는 것이 명백합니다.

단, 표준 회전 플랫폼 케이스(FOG)에서 비원형 광로를 사용하는 경우와 같이 우주에서 광원의 경로가 광신호의 경로를 따르지 않는 경우에는 이 방정식은 무효이다.이 경우 위상차 공식은 반드시 스토크스의 ^[28]정리에 의해 광로에 둘러싸인 영역을 포함한다.

그림 4: 밀폐된 광섬유가 늘어나지 않고 공간 내에서 임의로 이동한다.

2개의 역전파 광빔이 광섬유의 루프에 의해 결정되는 공통 광로를 공유하는 링 간섭계를 고려합니다(그림 4 참조).루프는 임의 모양을 가질 수 있으며 공간 내에서 임의로 이동할 수 있습니다.유일한 제약은 신축이 허용되지 않는다는 것이다.(원환 간섭계가 빈 공간에서 중심을 중심으로 회전하는 경우는 섬유 굴절률을 1로 하여 회수한다.)

파이버의 작은 세그먼트에 대해 생각해 보겠습니다.그 중 나머지 프레임의 $d\ell '$ 는 d $d\ell '$ $d\ell '$ $displaystyle$ d $\ell$ 입니다 $d\ell '$ $dt'_{\pm }$ $dt'_{\pm }$ ± $dt'_{\pm }$ \ $displaystyle dt ' _$ { \ pm $dt'_{\pm }$ } $dt'_{\pm }$ } , 、휴대 프레임의 세그먼트를 통과하는 데 좌우 이동 광선이 일치하며 다음과 같이 표시됩니다.

dt'_{\pm}={n\over c}d\ell'

d

{\textstyle d\ell =|d\mathbf {x} |}

{\textstyle d\ell =|d\mathbf {x} |}

{\textstyle d\ell =|d\mathbf {x} |}

x {\

textstyle

d

\ell

=

d\mathbf {x} }

을

{\textstyle d\ell =|d\mathbf {x} |}

(를) 실험실 프레임에 있는 이 작은 세그먼트의 길이라고

{\textstyle d\ell =|d\mathbf {x} |}

.상대론적 길이 수축식에 따르면 d

{\textstyle d\ell '=\gamma d\ell \approx d\ell }

{\textstyle d\ell '=\gamma d\ell \approx d\ell }

d

{\textstyle d\ell '=\gamma d\ell \approx d\ell }

d

{\textstyle d\ell '=\gamma d\ell \approx d\ell }

d

{\textstyle d\ell '=\gamma d\ell \approx d\ell }

d {\ d

{\

\

textstyle

d

\ell

'

=

\ displaystyle

d\ell

\

approx

d

\ell

}는

{\textstyle d\ell '=\gamma d\ell \approx d\ell }

세그먼트의

\mathbf {v}

v \

displaystyle

\

mathbf { v

}

}

의

\mathbf {v}

1순서로 보정된다.실험실 프레임에서 세그먼트를 통과하는 시간

dt_{\pm }

dt_{\pm }

t

dt_{\pm }

± {\

displaystyle dt_{\pm

}}은

dt_{\pm }

(는) 로렌츠 변환을 통해 다음과 같이 제공됩니다.

(\displaystyle dt_{\pm}=\pm \left(dt'\pm)\pm {frac d\mathbf {x} {c^{2}}\right)\approx \frac {n}{c} d\ell \frac {cdbf} dx} \cdpm

일반적으로

빔은 약간 다른 시간에 주어진 세그먼트를 방문하지만, 스트레칭이 없는 경우

{\textstyle d\ell }

d

{\

{\

textstyle

\mathbf {v}

d

\ell

\mathbf {v}

는 두 빔에서 동일합니다.

따라서 두 빔의 사이클을 완료하기 위한 시간 차이는 다음과 같습니다.

\displaystyle \Delta T=\int \left(dt_{+}-dt_{-}\right)\approx \frac {2}{c^{2}\point \mathbf {v} \cdot d\mathbf {x}

주목할 만한 것은 시간차가

굴절률

n(\

displaystyle

n

)

및

n

섬유 내 광속과는 무관하다는 점입니다.

광원에 배치된 테두리를 보기 위한 화면을 상상해 보십시오(또는 빔플리터를 사용하여 소스 포인트에서 화면으로 빛을 보내십시오).광원이 일정할 경우 간섭 테두리는 δ ${\textstyle \Delta \phi \approx {\frac {2\pi c}{\lambda }}\Delta T}$ 2 ${\textstyle \Delta \phi \approx {\frac {2\pi c}{\lambda }}\Delta T}$ c ${\textstyle \Delta \phi \approx {\frac {2\pi c}{\lambda }}\Delta T}$ T \ $textstyle$ \ $Delta \phi \ approx$ \ $frac {$ 2 \ pi c } { \ $lambda }}$ \ $Delta$ T에 의해 주어진 프린지 변위에 의해 화면에 형성됩니다. 여기서 첫 번째 인자는 빛의 주파수입니다.이것은 일반화된 Sagnac^[31] 공식을 제공한다.

\displaystyle \Delta \phi \apprough {4\pi }{\lambda c}}\point \mathbf {v} \cdot d\mathbf {x}

파이버가

{\boldsymbol {\omega }}

{\

{\

displaystyle

{\

boldsymbol {\

{v}

}}

=\times

\

mathbf

{x

} }

인

{\textstyle \mathbf {v} ={\boldsymbol {\omega }}\times \mathbf {x} }

{\textstyle \mathbf {v} ={\boldsymbol {\omega }}\times \mathbf {x} }

처럼 움직이는 특수한 경우에는 루프 면적으로 적분을 계산할 수 있습니다.

\displaystyle \point \mathbf {v} \cdot d\mathbf {x} =\point \boldsymbol {x} \mathbf {x} \mathbf {x} = \point \boldsymbol {x} \times \mathbf {x}

이것은 임의의 형태와 기하학의 링 간섭계에 대한 Sagnac 공식을 제공합니다.

\displaystyle \Delta \phi \약 \frac {8\pi }{\lambda c}}{\boldsymbol \mega }}\cdot \mathbf {A}}

스트레칭도 허용하면 피조 간섭 ^[31]공식을 복구합니다.

적용들

정확한 동기화를 확인하면서 지구를 일주하는 펄스의 릴레이도 Sagnac 효과를 보정해야 할 경우로 인식된다.1984년에 3개의 지상국과 여러 개의 GPS 위성을 포함한 검증이 이루어졌고,^[32] 전 세계에서 신호가 동서로 전달되었다.Sagnac 간섭계의 경우 간섭 테두리를 생성하여 프린지 시프트를 관찰함으로써 도달시간 차이를 측정한다.전 세계에 펄스를 중계하는 경우에는 펄스의 실제 도달시간에서 직접 도달시간의 차이를 구한다.두 경우 모두 도착 시간 차이의 메커니즘은 동일하다: Sagnac 효과.

Hafele-Keying 실험은 Sagnac 효과 물리학에 ^[32]대한 대응책으로도 인식된다.실제 Hafele-Keating 실험에서^[33] 운송 모드(장거리 비행)는 자체적인 시간 연장 효과를 발생시켰으며, 다양한 기여도를 분리하기 위해 계산이 필요했다.(이론적으로) 너무 느리게 전송되는 클럭의 경우 전송에서 발생하는 시간 확장 효과가 무시할 수 있을 정도로 클럭의 경우, 클럭이 출발점에 다시 도착했을 때의 시간 차이는 세계를 이동하는 펄스의 릴레이에서 발견된 시간 차이와 같습니다: 207나노초.

실용적인 용도

Sagnac 효과는 현재 기술에 사용되고 있습니다.한 가지 용도는 관성 유도 시스템에 있다.링 레이저 자이로스코프는 회전에 매우 민감하며, 관성 유도 시스템이 정확한 결과를 반환하려면 회전을 고려해야 합니다.링 레이저는 "모드 1"이라고도 할 수 있는 항성일을 검출할 수도 있습니다.GPS, GLONASS, 나침반 또는 갈릴레오와 같은 지구 항법 위성 시스템(GNSS)은 시계를 동기화하기 위해 무선 신호를 사용하는 절차에서 지구의 자전을 고려해야 한다.

링 레이저

그림 6링 레이저 설정의 개략도.

광섬유 자이로스코프는 '패시브 링 간섭계'라고도 합니다.패시브 링 간섭계는 외부에서 설정으로 들어오는 빛을 사용합니다.얻어진 간섭 패턴은 프린지 패턴이며 측정되는 것은 위상 편이입니다.

완전히 다른 배열에 기초하여 자급식 링 간섭계를 구성할 수도 있습니다.이것은 링 레이저 또는 링 레이저 자이로스코프라고 불립니다.빛은 빛의 경로에 레이저 들뜸을 포함시킴으로써 생성되고 지속됩니다.

링 레이저 캐비티에서 발생하는 현상을 이해하려면 연속적인 빛의 발생을 수반하는 레이저 설정에서 레이저 프로세스의 물리학에 대해 설명하면 도움이 됩니다.레이저 들뜸이 시작되면 캐비티 내의 분자는 광자를 방출하지만, 이들 분자는 열속도를 가지기 때문에 레이저 캐비티 내의 빛은 우선 속도의 통계적 분포에 따라 주파수 범위가 된다.자극 방출의 과정은 한 주파수를 다른 주파수보다 빠르게 앞지르게 하고, 그 이후 빛은 단색에 매우 가깝다.

그림 7링 레이저 간섭계가 회전하고 있을 때의 주파수 시프트의 개략도.역전파광과 공동전파광은 모두 주파수의 12주기를 거칩니다.

단순화를 위해 모든 방출된 광자가 링과 평행한 방향으로 방출된다고 가정합니다.그림 7은 링 레이저의 회전 효과를 나타내고 있습니다.리니어 레이저에서는 파장의 정수배수가 레이저 캐비티 길이에 적합하다.즉, 앞뒤로 이동할 때 레이저 광선이 주파수의 정수 사이클을 통과합니다.링 레이저의 경우도 마찬가지입니다.레이저 빛의 주파수의 사이클 수는 양방향으로 동일합니다.링 레이저 설정이 회전하고 있을 때는, 쌍방향으로 같은 사이클수의 품질이 유지됩니다.이미지는 전파의 양방향에서 사이클 수가 동일하도록 파장 이동(즉, 주파수 이동)이 있음을 나타냅니다.

레이저광의 두 주파수를 간섭시키는 것으로 비트 주파수를 얻을 수 있다. 비트 주파수는 두 주파수 간의 차이이다.이 비트 주파수는 시간의 간섭 패턴으로 간주할 수 있습니다.(간섭계의 간섭 테두리가 더 친숙한 것은 공간 패턴입니다).이 비트 주파수의 주기는 관성 공간에 대한 링 레이저의 각 속도에 선형으로 비례합니다.이것은 현대의 관성 항법 시스템에 널리 사용되는 링 레이저 자이로스코프의 원리입니다.

포인트

점은 내.빨간색과 파란색 점은 역전파 광자를 나타내고 회색 점은 레이저 공동 내 분자를 나타냅니다.

패시브 링 간섭계에서 프린지 변위는 각도 위치의 첫 번째 도함수에 비례합니다. 링 간섭계 설정의 0 각 속도에 해당하는 프린지 변위를 결정하기 위해서는 신중한 보정이 필요합니다.한편 링 레이저 간섭계는 제로 각속도에 해당하는 출력을 결정하기 위해 보정이 필요하지 않습니다.링 레이저 간섭계는 자가 교정식입니다.링 레이저 설정이 관성 공간에 대해 회전하지 않는 경우에만 비트 주파수는 0이 됩니다.

그림 8은 링 레이저 간섭계를 자가 교정하는 물리적 특성을 보여줍니다.회색 점은 레이저 공동에서 공진기로 작용하는 분자를 나타냅니다.링 캐비티의 모든 부분을 따라 빛의 속도는 양방향에서 동일합니다.링 레이저 디바이스가 회전하고 있을 때는, 그 배경에 대해서 회전합니다.즉, 빛의 속도의 불변성은 링 레이저 간섭계의 자기 교정 특성에 대한 기준을 제공합니다.

록인

링 레이저 자이로스코프는 낮은 회전 속도(100°/h 미만)에서 록인(lock-in)이라고 불리는 효과를 경험합니다.매우 낮은 회전 속도에서는 역전파 레이저 모드의 주파수가 거의 같아집니다.이 경우 역전파빔 간의 크로스톡에 의해 사출잠금이 발생하여 정재파가 바람직한 위상으로 "걸려" 각 빔의 주파수가 서서히 회전하는 것이 아니라 서로 고정된다.레이저 공동을 작은 각도(수백 헤르츠)로 전후로 회전 디더링함으로써 회전 속도가 0에 가까운 짧은 시간 동안만 록인이 발생합니다. 따라서 오차는 번갈아 발생하는 데드 기간 사이에 서로를 약하게 상쇄시킵니다.

광섬유 자이로스코프 대 링 레이저 자이로스코프

광섬유 자이로(FOGs)와 링 레이저 자이로(RLGs)는 둘 다 닫힌 광로를 중심으로 시계방향과 시계반대방향으로 이동하는 광빔 간의 전파시간 차이를 감시함으로써 작동한다.이들은 비용, 신뢰성, 크기, 중량, 전력 및 특정 애플리케이션에 대해 이러한 개별 기술을 평가할 때 고려해야 하는 기타 성능 특성에 따라 크게 다릅니다.

RLG는 정확한 가공, 정밀 미러 사용, 클린 룸 조건에서의 조립이 필요합니다.기계적 디더링 어셈블리는 무게를 다소 증가시키지만 ^{[citation needed]}눈에 띄게 증가하지는 않습니다.RLG는 실온에 가까운 조건에서 ^{[citation needed]}100,000시간 이상의 동작을 로깅할 수 있습니다.레이저의 ^[34]소비전력은 비교적 높습니다.

간섭계 FOG는 순수 고체이며, 기계적 디더링 컴포넌트가 필요하지 않으며, 정밀 가공이 필요하지 않으며, 유연한 형상을 가지며, 매우 작게 만들 수 있습니다.통신업계의 많은 표준 부품을 사용하고 있습니다.또한 FOG의 주요 광학 컴포넌트는 통신 업계에서 성능이 입증되었으며, 수명은 수십 ^[35]년 후에 측정되었습니다.그러나 여러 광학 부품을 정밀 자이로 기기로 조립하는 것은 비용이 많이 듭니다.아날로그 FOG는 가능한 한 낮은 비용을 제공하지만 성능에 제한이 있습니다.디지털 FOG는 엄격한 ^[36]애플리케이션에 필요한 광범위한 동적 범위와 정확한 스케일 팩터 보정을 제공합니다.더 길고 큰 코일을 사용하면 감도가 높아지지만 온도 변화와 진동에 대한 민감도가 높아집니다.

영면적 사냐크 간섭계 및 중력파 검출

Sagnac 위상은 실제로 ^[37]1886년에 Michelson에 의해 처음 설명되었고, 그는 피조 ^[38]실험의 반복에서 이 간섭계의 짝수 반사 변형을 사용했다.Michelson은 다음과 같은 형태의 간섭계에 의해 생성되는 프링의 극단적인 안정성에 주목했다.거울이 정렬되자마자 흰색 빛 테두리가 관찰되었습니다.이중 경로 간섭계에서는 두 경로 길이가 몇 마이크로미터(백색의 간섭 길이) 이내에 일치해야 하기 때문에 백색의 테두리를 얻기가 어렵습니다.단, Sagnac 설정은 공통 패스인터페로미터이기 때문에 기본적으로 2개의 패스길이에 일치합니다.마찬가지로 Michelson은 광로 아래에서 불이 켜진 성냥을 유지하는 동안에도 프린지 패턴이 안정적으로 유지될 것이라고 관찰했다. 대부분의 간섭계에서는 성냥 위의 따뜻한 공기로부터의 굴절률 변동으로 인해 프린지가 심하게 이동한다.Sagnac 간섭계는 미러 또는 빔 스플리터의 ^[39]변위에 거의 완전히 둔감합니다.이러한 Sagnac 토폴로지의 특성으로 인해 매우 높은 안정성을 필요로 하는 응용 프로그램에서 이러한 토폴로지를 사용할 수 있게 되었습니다.

그림 9.제로 영역 사그낙 간섭계

회전에 의한 Sagnac 간섭계의 프린지 시프트는 광로의 둘러싸인 영역에 비례하는 크기를 가지며, 이 영역은 회전 축에 대해 지정되어야 한다.따라서 루프가 반대방향(시계방향 또는 반시계방향)으로 감길 경우 루프 영역의 부호가 반전됩니다.따라서 양방향 루프를 포함하는 광로에는 시계방향 루프와 시계반대방향 루프의 면적 차이로 주어진 순면적이 있습니다.동일하지만 반대되는 두 개의 루프가 있는 특수한 경우를 영면적 사그낙 간섭계라고 합니다.그 결과 ^[40]Sagnac 토폴로지의 안정성을 나타내면서도 회전에 민감하지 않은 간섭계입니다.

레이저 간섭계 중력파 관측소(LIGO)는 2개의 4km Michelson-Fabry-Péro 간섭계로 구성되며 빔 스플리터에서 약 100와트의 레이저 전력으로 작동했다.Advanced LIGO로 업그레이드한 후에는 몇 킬로와트의 레이저 전력이 필요합니다.

Advanced LIGO 이상의 ^[41]3세대 기능 강화를 위해 다양한 경쟁 광학 시스템이 검토되고 있습니다.이러한 경쟁 제안 중 하나는 제로 영역 Sagnac 설계에 기초하고 있습니다.같은 면적의 2개의 루프로 이루어진 광로를 반대 방향으로 하면 유효 면적이 0이 되어 통상적인 의미에서 Sagnac 효과를 상쇄한다.저주파 미러 드리프트, 레이저 주파수 변화, 암 사이의 반사율 불균형 및 열유발 복굴절에는 무감각하지만 이 구성은 천문학적인 ^[40]관심 주파수에서 중력파를 통과하는 데 민감합니다.그러나 광학계의 선택에는 많은 고려사항이 수반되며, 제로 영역 Sagnac의 특정 영역에서의 우월성에도 불구하고, 3세대 LIGO에 ^[42]^[43]대한 광학계의 합의된 선택은 아직 없다.

「」를 참조해 주세요.

레퍼런스

^ ^a ^b Sagnac, Georges (1913), "L'éther lumineux démontré par l'effet du vent relatif d'éther dans un interféromètre en rotation uniforme" [The demonstration of the luminiferous aether by an interferometer in uniform rotation], Comptes Rendus, 157: 708–710
^ ^a ^b Sagnac, Georges (1913), "Sur la preuve de la réalité de l'éther lumineux par l'expérience de l'interférographe tournant" [On the proof of the reality of the luminiferous aether by the experiment with a rotating interferometer], Comptes Rendus, 157: 1410–1413
^ Anderson, R.; Bilger, H.R.; Stedman, G.E. (1994). "Sagnac effect: A century of Earth-rotated interferometers". Am. J. Phys. 62 (11): 975–985. Bibcode:1994AmJPh..62..975A. doi:10.1119/1.17656.
^ Lodge, Oliver (1897). "Experiments on the Absence of Mechanical Connexion between Ether and Matter" . Philos. Trans. R. Soc. 189: 149–166. Bibcode:1897RSPTA.189..149L. doi:10.1098/rsta.1897.0006.
^ Michelson, A.A. (1904). "Relative Motion of Earth and Aether". Philosophical Magazine. 8 (48): 716–719. doi:10.1080/14786440409463244.
^ ^a ^b ^c ^d ^e Laue, Max von (1920). "Zum Versuch von F. Harress". Annalen der Physik. 367 (13): 448–463. Bibcode:1920AnP...367..448L. doi:10.1002/andp.19203671303. 영어 번역:F의 실험에 대해서. 하레스
^ ^a ^b ^c ^d Laue, Max von (1911). "Über einen Versuch zur Optik der bewegten Körper". Münchener Sitzungsberichte: 405–412. 영어 번역:움직이는 물체의 광학실험
^ ^a ^b Pauli, Wolfgang (1981). Theory of Relativity. New York: Dover. ISBN 978-0-486-64152-2.
^ 알버트 아인슈타인의 과학 출판물 목록
^ 천문학자 나히히텐, 199, 8-10
^ 천문학자 나히히텐, 199, 47~48
^ Guido Rizzi; Matteo Luca Ruggiero (2003). "The relativistic Sagnac Effect: two derivations". In G. Rizzi; M.L. Ruggiero (eds.). Relativity in Rotating Frames. Dordrecht: Kluwer Academic Publishers. arXiv:gr-qc/0305084. Bibcode:2003gr.qc.....5084R. ISBN 978-0-486-64152-2.
^ Ashby, N. (2003). "Relativity in the Global Positioning System". Living Rev. Relativ. 6 (1): 1. Bibcode:2003LRR.....6....1A. doi:10.12942/lrr-2003-1. PMC 5253894. PMID 28163638. (오픈 액세스)
^ L.D. Landau, E.M. Lifshitz, (1962)"고전장론"제2판, Pergamon Press, 페이지 296–297
^ Langevin, Paul (1921). "Sur la théorie de la relativité et l'expérience de M. Sagnac". Comptes Rendus. 173: 831–834.
^ Langevin, Paul (1937). "Sur l'expérience de M. Sagnac". Comptes Rendus. 205: 304–306.
^ 알버트 아인슈타인, 1905, "움직이는 물체의 전기역학에 대하여" http://www.fourmilab.ch/etexts/einstein/specrel/www/
^ A. 아인슈타인, '일반상대성이론', 94; 앤솔로지 '상대성이론', A.1920년 캘커타 대학교 아인슈타인과 H. 민코프스키
^ "일반상대성", 케임브리지 대학 출판부 루이스 라이더(2009).페이지 7
^ http://www.physicsdiscussionforum.org/download/file.php?id=250^{[베어 URL PDF]}
^ "The Sagnac Effect".
^ Michelson, Albert Abraham; Gale, Henry G. (1925). "The Effect of the Earth's Rotation on the Velocity of Light, II". The Astrophysical Journal. 61: 140–145. Bibcode:1925ApJ....61..140M. doi:10.1086/142879.
^ Stedman, G. E. (1997). "Ring-laser tests of fundamental physics and geophysics". Rep. Prog. Phys. 60 (6): 615–688. Bibcode:1997RPPh...60..615S. CiteSeerX 10.1.1.128.191. doi:10.1088/0034-4885/60/6/001.
^ Malykin, G. B. (2002). "Sagnac effect in a rotating frame of reference. Relativistic Zeno paradox" (PDF). Physics-Uspekhi. 45 (8): 907–909. Bibcode:2002PhyU...45..907M. doi:10.1070/pu2002v045n08abeh001225. Retrieved 15 February 2013.
^ ^a ^b Tartaglia, A.; Ruggiero, M. L. (2004). "Sagnac effect and pure geometry". arXiv:gr-qc/0401005.
^ ^a ^b Brown, Kevin. "The Sagnac Effect". MathPages. Retrieved 15 February 2013.
^ http://www.orgonelab.org/EtherDrift/Post1967.pdf^{[베어 URL PDF]}
^ ^a ^b Anandan, J. (1981). "Sagnac effect in relativistic and nonrelativistic physics". Phys. Rev. D. 24 (2): 338–346. Bibcode:1981PhRvD..24..338A. doi:10.1103/physrevd.24.338.
^ Wang, R.; Zheng, Y.; Yao, A.; Langley, D (2006). "Modified Sagnac experiment for measuring travel-time difference between counter-propagating light beams in a uniformly moving fiber". Physics Letters A. 312 (1–2): 7–10. arXiv:physics/0609222. Bibcode:2003PhLA..312....7W. doi:10.1016/S0375-9601(03)00575-9. S2CID 699912.
^ Brown, Kevin. "Sagnac and Fizeau". MathPages. Retrieved 15 February 2013.
^ ^a ^b Ori, A. (2016). "Generalized Sagnac-Wang-Fizeau formula". Physical Review A. 94 (6): 063837. arXiv:1601.01448. Bibcode:2016PhRvA..94f3837O. doi:10.1103/physreva.94.063837. S2CID 119242639.
^ ^a ^b Allan, D. W., Weiss, M. A., & Ashby, N. (1985). "Around-the-World Relativistic Sagnac Experiment". Science. 228 (4695): 69–71. Bibcode:1985Sci...228...69A. doi:10.1126/science.228.4695.69. PMID 17811569. S2CID 22556404.{{cite journal}}: CS1 maint: 여러 이름: 작성자 목록(링크)
^ Hafele J., Keating, R. (1972-07-14). "Around the world atomic clocks:predicted relativistic time gains". Science. 177 (4044): 166–168. Bibcode:1972Sci...177..166H. doi:10.1126/science.177.4044.166. PMID 17779917. S2CID 10067969. Retrieved 2006-09-18.{{cite journal}}: CS1 maint: 여러 이름: 작성자 목록(링크)
^ Juang, J.-N.; Radharamanan, R. "Evaluation of Ring Laser and Fiber Optic Gyroscope Technology" (PDF). Retrieved 15 February 2013.
^ Napolitano, F. "Fiber-Optic Gyroscopes Key Technological Advantages" (PDF). iXSea. Archived from the original (PDF) on 5 March 2012. Retrieved 15 February 2013.
^ Udd, E.; Watanabe, S. F.; Cahill, R. F. (1986). "Comparison of ring laser and fiber-optic gyro technology". In Agard Guided Optical Structures in the Military Environment 14 P (See N87-13273 04-74. McDonnell-Douglas. Bibcode:1986gosm.agar.....U.
^ Hariharan, P. (1975). "Sagnac or Michelson–Sagnac interferometer?". Applied Optics. 14 (10): 2319_1–2321. Bibcode:1975ApOpt..14.2319H. doi:10.1364/AO.14.2319_1. PMID 20155007.
^ Michelson, A. A. & Morley, E.W. (1886). "Influence of Motion of the Medium on the Velocity of Light" . Am. J. Sci. 31 (185): 377–386. Bibcode:1886AmJS...31..377M. doi:10.2475/ajs.s3-31.185.377. S2CID 131116577.
^ Hariharan, P. (2003). Optical Interferometry (Second ed.). Academic Press. pp. 28–29. ISBN 978-0-12-311630-7.
^ ^a ^b Sun, K-X.; Fejer, M.M.; Gustafson, E.; Byer R.L. (1996). "Sagnac Interferometer for Gravitational-Wave Detection" (PDF). Physical Review Letters. 76 (17): 3053–3056. Bibcode:1996PhRvL..76.3053S. doi:10.1103/PhysRevLett.76.3053. PMID 10060864. Retrieved 31 March 2012.
^ Punturo, M.; Abernathy, M.; Acernese, F.; Allen, B.; Andersson, N.; Arun, K.; Barone, F.; Barr, B.; Barsuglia, M.; Beker, M.; Beveridge, N.; Birindelli, S.; Bose, S.; Bosi, L.; Braccini, S.; Bradaschia, C.; Bulik, T.; Calloni, E.; Cella, G.; Chassande Mottin, E.; Chelkowski, S.; Chincarini, A.; Clark, J.; Coccia, E.; Colacino, C.; Colas, J.; Cumming, A.; Cunningham, L.; Cuoco, E.; et al. (2010). "The third generation of gravitational wave observatories and their science reach". Classical and Quantum Gravity. 27 (8): 084007. Bibcode:2010CQGra..27h4007P. doi:10.1088/0264-9381/27/8/084007. hdl:11858/00-001M-0000-0011-2EAE-2.
^ Freise, A.; Chelkowski, S.; Hild, S.; Pozzo, W. D.; Perreca, A.; Vecchio, A. (2009). "Triple Michelson interferometer for a third-generation gravitational wave detector". Classical and Quantum Gravity. 26 (8): 085012. arXiv:0804.1036. Bibcode:2009CQGra..26h5012F. doi:10.1088/0264-9381/26/8/085012. S2CID 7535227.
^ Eberle, T.; Steinlechner, S.; Bauchrowitz, J. R.; Händchen, V.; Vahlbruch, H.; Mehmet, M.; Müller-Ebhardt, H.; Schnabel, R. (2010). "Quantum Enhancement of the Zero-Area Sagnac Interferometer Topology for Gravitational Wave Detection". Physical Review Letters. 104 (25): 251102. arXiv:1007.0574. Bibcode:2010PhRvL.104y1102E. doi:10.1103/PhysRevLett.104.251102. PMID 20867358. S2CID 9929939.

외부 링크

산술 페이지:Sagnac 효과
기초물리학과 지구물리학의 링레이저 테스트(G E Stedman의 확장 리뷰).PDF 파일, 1.5 MB)
Ashby, N. (2003). "Relativity in the Global Positioning System". Living Rev. Relativ. 6 (1): 1. Bibcode:2003LRR.....6....1A. doi:10.12942/lrr-2003-1. PMC 5253894. PMID 28163638. (오픈 액세스)

[sagnac1-1] Sagnac, Georges (1913), "L'éther lumineux démontré par l'effet du vent relatif d'éther dans un interféromètre en rotation uniforme" [The demonstration of the luminiferous aether by an interferometer in uniform rotation], Comptes Rendus, 157: 708–710

[sagnac2-2] Sagnac, Georges (1913), "Sur la preuve de la réalité de l'éther lumineux par l'expérience de l'interférographe tournant" [On the proof of the reality of the luminiferous aether by the experiment with a rotating interferometer], Comptes Rendus, 157: 1410–1413

[3] Anderson, R.; Bilger, H.R.; Stedman, G.E. (1994). "Sagnac effect: A century of Earth-rotated interferometers". Am. J. Phys. 62 (11): 975–985. Bibcode:1994AmJPh..62..975A. doi:10.1119/1.17656.

[4] Lodge, Oliver (1897). "Experiments on the Absence of Mechanical Connexion between Ether and Matter" . Philos. Trans. R. Soc. 189: 149–166. Bibcode:1897RSPTA.189..149L. doi:10.1098/rsta.1897.0006.

[5] Michelson, A.A. (1904). "Relative Motion of Earth and Aether". Philosophical Magazine. 8 (48): 716–719. doi:10.1080/14786440409463244.

[laue2-6] Laue, Max von (1920). "Zum Versuch von F. Harress". Annalen der Physik. 367 (13): 448–463. Bibcode:1920AnP...367..448L. doi:10.1002/andp.19203671303. 영어 번역:F의 실험에 대해서. 하레스

[laue1-7] Laue, Max von (1911). "Über einen Versuch zur Optik der bewegten Körper". Münchener Sitzungsberichte: 405–412. 영어 번역:움직이는 물체의 광학실험

[pauli-8] Pauli, Wolfgang (1981). Theory of Relativity. New York: Dover. ISBN 978-0-486-64152-2.

[9] 알버트 아인슈타인의 과학 출판물 목록

[10] 천문학자 나히히텐, 199, 8-10

[11] 천문학자 나히히텐, 199, 47~48

[rizzi-12] Guido Rizzi; Matteo Luca Ruggiero (2003). "The relativistic Sagnac Effect: two derivations". In G. Rizzi; M.L. Ruggiero (eds.). Relativity in Rotating Frames. Dordrecht: Kluwer Academic Publishers. arXiv:gr-qc/0305084. Bibcode:2003gr.qc.....5084R. ISBN 978-0-486-64152-2.

[ashby-13] Ashby, N. (2003). "Relativity in the Global Positioning System". Living Rev. Relativ. 6 (1): 1. Bibcode:2003LRR.....6....1A. doi:10.12942/lrr-2003-1. PMC 5253894. PMID 28163638. (오픈 액세스)

[14] L.D. Landau, E.M. Lifshitz, (1962)"고전장론"제2판, Pergamon Press, 페이지 296–297

[15] Langevin, Paul (1921). "Sur la théorie de la relativité et l'expérience de M. Sagnac". Comptes Rendus. 173: 831–834.

[16] Langevin, Paul (1937). "Sur l'expérience de M. Sagnac". Comptes Rendus. 205: 304–306.

[17] 알버트 아인슈타인, 1905, "움직이는 물체의 전기역학에 대하여" http://www.fourmilab.ch/etexts/einstein/specrel/www/

[18] A. 아인슈타인, '일반상대성이론', 94; 앤솔로지 '상대성이론', A.1920년 캘커타 대학교 아인슈타인과 H. 민코프스키

[19] "일반상대성", 케임브리지 대학 출판부 루이스 라이더(2009).페이지 7

[20] ttp://www.physicsdiscussionforum.org/download/file.php?id=250^{[베어 URL PDF]}

[21] "The Sagnac Effect".

[22] Michelson, Albert Abraham; Gale, Henry G. (1925). "The Effect of the Earth's Rotation on the Velocity of Light, II". The Astrophysical Journal. 61: 140–145. Bibcode:1925ApJ....61..140M. doi:10.1086/142879.

[Stedman19972-23] Stedman, G. E. (1997). "Ring-laser tests of fundamental physics and geophysics". Rep. Prog. Phys. 60 (6): 615–688. Bibcode:1997RPPh...60..615S. CiteSeerX 10.1.1.128.191. doi:10.1088/0034-4885/60/6/001.

[Malykin20022-24] Malykin, G. B. (2002). "Sagnac effect in a rotating frame of reference. Relativistic Zeno paradox" (PDF). Physics-Uspekhi. 45 (8): 907–909. Bibcode:2002PhyU...45..907M. doi:10.1070/pu2002v045n08abeh001225. Retrieved 15 February 2013.

[TartagliaRuggiero-25] Tartaglia, A.; Ruggiero, M. L. (2004). "Sagnac effect and pure geometry". arXiv:gr-qc/0401005.

[BrownSagnac-26] Brown, Kevin. "The Sagnac Effect". MathPages. Retrieved 15 February 2013.

[27] ttp://www.orgonelab.org/EtherDrift/Post1967.pdf^{[베어 URL PDF]}

[Anandan-28] Anandan, J. (1981). "Sagnac effect in relativistic and nonrelativistic physics". Phys. Rev. D. 24 (2): 338–346. Bibcode:1981PhRvD..24..338A. doi:10.1103/physrevd.24.338.

[Wang-29] Wang, R.; Zheng, Y.; Yao, A.; Langley, D (2006). "Modified Sagnac experiment for measuring travel-time difference between counter-propagating light beams in a uniformly moving fiber". Physics Letters A. 312 (1–2): 7–10. arXiv:physics/0609222. Bibcode:2003PhLA..312....7W. doi:10.1016/S0375-9601(03)00575-9. S2CID 699912.

[BrownSagnacFizeau-30] Brown, Kevin. "Sagnac and Fizeau". MathPages. Retrieved 15 February 2013.

[:0-31] Ori, A. (2016). "Generalized Sagnac-Wang-Fizeau formula". Physical Review A. 94 (6): 063837. arXiv:1601.01448. Bibcode:2016PhRvA..94f3837O. doi:10.1103/physreva.94.063837. S2CID 119242639.

[allan-32] Allan, D. W., Weiss, M. A., & Ashby, N. (1985). "Around-the-World Relativistic Sagnac Experiment". Science. 228 (4695): 69–71. Bibcode:1985Sci...228...69A. doi:10.1126/science.228.4695.69. PMID 17811569. S2CID 22556404.{{cite journal}}: CS1 maint: 여러 이름: 작성자 목록(링크)

[33] Hafele J., Keating, R. (1972-07-14). "Around the world atomic clocks:predicted relativistic time gains". Science. 177 (4044): 166–168. Bibcode:1972Sci...177..166H. doi:10.1126/science.177.4044.166. PMID 17779917. S2CID 10067969. Retrieved 2006-09-18.{{cite journal}}: CS1 maint: 여러 이름: 작성자 목록(링크)

[JuangRadharamanan-34] Juang, J.-N.; Radharamanan, R. "Evaluation of Ring Laser and Fiber Optic Gyroscope Technology" (PDF). Retrieved 15 February 2013.

[Napolitano-35] Napolitano, F. "Fiber-Optic Gyroscopes Key Technological Advantages" (PDF). iXSea. Archived from the original (PDF) on 5 March 2012. Retrieved 15 February 2013.

[36] Udd, E.; Watanabe, S. F.; Cahill, R. F. (1986). "Comparison of ring laser and fiber-optic gyro technology". In Agard Guided Optical Structures in the Military Environment 14 P (See N87-13273 04-74. McDonnell-Douglas. Bibcode:1986gosm.agar.....U.

[hariharan1975-37] Hariharan, P. (1975). "Sagnac or Michelson–Sagnac interferometer?". Applied Optics. 14 (10): 2319_1–2321. Bibcode:1975ApOpt..14.2319H. doi:10.1364/AO.14.2319_1. PMID 20155007.

[mich-38] Michelson, A. A. & Morley, E.W. (1886). "Influence of Motion of the Medium on the Velocity of Light" . Am. J. Sci. 31 (185): 377–386. Bibcode:1886AmJS...31..377M. doi:10.2475/ajs.s3-31.185.377. S2CID 131116577.

[Hariharan2003-39] Hariharan, P. (2003). Optical Interferometry (Second ed.). Academic Press. pp. 28–29. ISBN 978-0-12-311630-7.

[Sun1996-40] Sun, K-X.; Fejer, M.M.; Gustafson, E.; Byer R.L. (1996). "Sagnac Interferometer for Gravitational-Wave Detection" (PDF). Physical Review Letters. 76 (17): 3053–3056. Bibcode:1996PhRvL..76.3053S. doi:10.1103/PhysRevLett.76.3053. PMID 10060864. Retrieved 31 March 2012.

[punturo2010-41] Punturo, M.; Abernathy, M.; Acernese, F.; Allen, B.; Andersson, N.; Arun, K.; Barone, F.; Barr, B.; Barsuglia, M.; Beker, M.; Beveridge, N.; Birindelli, S.; Bose, S.; Bosi, L.; Braccini, S.; Bradaschia, C.; Bulik, T.; Calloni, E.; Cella, G.; Chassande Mottin, E.; Chelkowski, S.; Chincarini, A.; Clark, J.; Coccia, E.; Colacino, C.; Colas, J.; Cumming, A.; Cunningham, L.; Cuoco, E.; et al. (2010). "The third generation of gravitational wave observatories and their science reach". Classical and Quantum Gravity. 27 (8): 084007. Bibcode:2010CQGra..27h4007P. doi:10.1088/0264-9381/27/8/084007. hdl:11858/00-001M-0000-0011-2EAE-2.

[Friese2009-42] Freise, A.; Chelkowski, S.; Hild, S.; Pozzo, W. D.; Perreca, A.; Vecchio, A. (2009). "Triple Michelson interferometer for a third-generation gravitational wave detector". Classical and Quantum Gravity. 26 (8): 085012. arXiv:0804.1036. Bibcode:2009CQGra..26h5012F. doi:10.1088/0264-9381/26/8/085012. S2CID 7535227.

[Eberle2010-43] Eberle, T.; Steinlechner, S.; Bauchrowitz, J. R.; Händchen, V.; Vahlbruch, H.; Mehmet, M.; Müller-Ebhardt, H.; Schnabel, R. (2010). "Quantum Enhancement of the Zero-Area Sagnac Interferometer Topology for Gravitational Wave Detection". Physical Review Letters. 104 (25): 251102. arXiv:1007.0574. Bibcode:2010PhRvL.104y1102E. doi:10.1103/PhysRevLett.104.251102. PMID 20867358. S2CID 9929939.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

v t 특수 상대성 검정
속도/등방성	마이클슨-몰리 실험 케네디-손다이크 실험 모에스바우어 로터 실험 공진기 실험 드 시터 이중성 실험 함마 실험 중성미자 속도 측정
로렌츠 불변성	로렌츠 위반에 대한 최신 검색 휴즈-드레버 실험 트라우톤-노블 실험 레일리와 브레이스의 실험 트라우톤-랭킨 실험 로렌츠 위반 반물질 시험 로렌츠 위반 중성미자 진동 로렌츠 바이올레이션 전기역학
시간 연장 길이 수축	Ives-Stilwell 실험 모에스바우어 로터 실험 시간 연장에 대한 실험 테스트 하펠-키팅 실험 길이 수축 확인
상대론적 에너지	상대론적 에너지 및 운동량 검정 카우프만-부체르-노이만 실험
피조/사냐크	피조 실험 Sagnac 실험 마이클슨-게일-피어슨 실험
대체 수단	에테르 이론의 반박 배출 이론의 반박
일반	단방향 빛의 속도 특수상대성이론의 검정 표준 모델 확장

Search

사냐크 효과

네임스페이스

더

목차

설명 및 조작

역사

이론.

기본 케이스

일반화 공식

적용들

실용적인 용도

링 레이저

포인트

록인

광섬유 자이로스코프 대 링 레이저 자이로스코프

영면적 사냐크 간섭계 및 중력파 검출

「」를 참조해 주세요.

레퍼런스

외부 링크

Search

사냐크 효과

설명 및 조작

역사

이론.

기본 케이스

일반화 공식

적용들

실용적인 용도

링 레이저

포인트

록인

광섬유 자이로스코프 대 링 레이저 자이로스코프

영면적 사냐크 간섭계 및 중력파 검출

「 」를 참조해 주세요.

레퍼런스

외부 링크

「」를 참조해 주세요.