피조 실험

피조 실험은 움직이는 물에서 빛의 상대 속도를 측정하기 위해 1851년 히폴리테 피조에 의해 수행되었다.피조는 특수한 간섭계 배치를 사용하여 빛의 속도에 대한 매개체의 움직임의 영향을 측정했다.

당시 널리 퍼져 있던 이론에 따르면 움직이는 매체를 통해 이동하는 빛은 매체에 의해 끌려가므로 측정된 빛의 속도는 매체를 통한 속도의 단순한 합과 매체의 속도의 합이 된다.피조는 정말로 끌리는 효과를 감지했지만 그가 관찰한 효과의 크기는 예상보다 훨씬 낮았다.그가 물 대신 공기를 넣어 실험을 반복했을 때 그는 아무런 효과도 관찰하지 못했다.그의 결과는 대부분의 물리학자들이 당황하고 있는 상황인 프레스넬의 부분적인 에테르 드랙 가설을 뒷받침해 주는 것 같다.알버트 아인슈타인의 특수 상대성 이론의 등장으로 피조의 뜻밖의 측정에 대한 만족스러운 설명이 개발되기까지 반세기가 넘는 시간이 흘렀다.아인슈타인은 나중에 특수상대성이론에 대한 실험의 중요성을 지적했는데, 이 실험은 작은 속도로 제한되었을 때 상대론적 속도-추가 공식에 해당한다.

피조 실험이라고 일컬어지지만, 피조는 다양한 상황에서 빛의 속도를 측정하는 것을 포함하는 매우 다양한 실험을 수행한 활동적인 실험자였다.

실험 설정

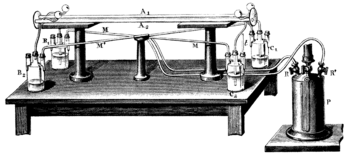
Fizau의 1851 실험에 대한 매우 단순한 표현은 그림 2에 제시되어 있다.들어오는 빛은 빔 스플리터(BS)에 의해 두 개의 빔으로 갈라지고 반대 방향으로 흐르는 두 개의 물기둥을 통과한다.그런 다음 두 빔을 재결합하여 관찰자가 해석할 수 있는 간섭 패턴을 형성한다.

그림 2에 설명된 단순화된 배열은 희미한 프링만 가능케 하는 단색광의 사용을 요구했을 것이다.백색광의 일관성이 짧기 때문에 백색광의 사용은 광학적 경로를 비실용적 정밀도에 맞춰야 했으며, 기구는 진동, 움직임 이동 및 온도 영향에 극도로 민감했을 것이다.

한편, 그림 3과 그림 4에 묘사된 피조의 실제 기구는 공통 경로 간섭계로 설정되었다.이를 통해 반대쪽 빔이 동등한 경로를 통과하도록 보장해 태양을 광원으로 사용해도 마찰이 쉽게 형성됐다.

빛의 이중 전달은 동작하는 매체에서 가로지르는 거리를 증가시키고, 나아가 두 관 사이의 온도나 압력의 우발적인 차이를 완전히 보상하기 위한 것이었는데, 그 때문에 프링글이 변위될 수 있고, 그 변위는 동작만으로 야기되는 변위와 혼합될 수 있다.uld는 생산되었고, 따라서 그것에 대한 관찰을 불확실하게 만들었다.^{[P 1]}

— Fizeau

소스 S′에서 발산되는 광선은 빔 스플리터 G에 의해 반사되고 렌즈 L에 의해 평행 빔으로 시준된다. 슬릿 O와₁ O를₂ 통과한 후 두 개의₁ 광선이₂ 튜브 A와 A를 통과하며, 이 광선은 화살표에 표시된 것처럼 물이 앞뒤로 흐르고 있다.광선은 렌즈 L′의 초점에서 거울 m을 반사하여, 한 광선은 항상 물줄기와 같은 방향으로, 다른 광선은 물줄기의 방향과 반대 방향으로 전파된다.튜브를 앞뒤로 통과한 후, 두 광선은 S에서 결합하여 그림으로 그린 아이피스를 통해 시각화할 수 있는 간섭 프링크를 생성한다.간섭 패턴을 분석하여 관의 각 다리를 따라 빛이 이동하는 속도를 결정할 수 있다.^{[P 1][P 2][S 1]}

프레스넬 드래그 계수

속도가 v인 파이프에 물이 흐른다고 가정한다.발광성 에테르에 대한 비역학 이론에 따르면, 물을 따라 "끌어지면" 빛의 속도를 높여야 하고, 물의 저항을 "넘어갈" 때는 감소시켜야 한다.광선의 전체 속도는 물을 통과하는 속도에 물의 속도를 더한 단순한 첨가제여야 한다.

즉, n이 물의 굴절 지수여서 c/n이 정지해 있는 물에서 빛의 속도라면, 한 팔에서 w의 예측 속도는 다음과 같을 것이다.

${\displaystyle w_{+}={\frac {c}{n}}+v\ ,}$

다른 팔의 예상 속도는

${\displaystyle w_{-}={\frac {c}{n}-v\ .}$

따라서 물의 흐름을 거슬러 이동하는 빛은 물의 흐름을 따라 이동하는 빛보다 더 느려야 한다.

관측자에서 빛이 재조합될 때 두 빔 사이의 간섭 패턴은 두 경로를 통한 전달 시간에 따라 달라지며, 물의 속도의 함수로서 빛의 속도를 계산하는 데 사용할 수 있다.^{[S 2]}

Fizau는 그것을 발견했다.

${\displaystyle w_{+}={\frac {c}{n}}{n}}+v\왼쪽(1-{\frac {1}{n^{2}}}\오른쪽)\.}$

빛이 물가에 끌려가는 것처럼 보였지만 끌림의 크기는 예상보다 훨씬 낮았다는 얘기다.

피조 실험은 물리학자들로 하여금 1810년 아라고의 실험을 설명하기 위해 호출한, 즉 정지된 에테르를 통해 움직이는 매체가 그 매체의 속도의 극히 일부만을 가지고 그것을 통해 전파되는 빛을 끌고 간다는, 이론적으로 만족스럽지 못한 낡은 아우구스틴-장 프레스넬(1818) 이론의 경험적 타당성을 받아들이도록 강요했다., f에 의해 주어진 끌기 계수

${\displaystyle f=1-{\frac {1}{n^{2}}\\ .}$

1895년에 헨드릭 로렌츠는 분산으로 인한 추가 용어의 존재를 다음과 같이 예측했다.^{[S 3]: 15–20}

${\displaystyle w_{+}={\frac {c}{n}}{n}{n1}{n^{1}:{n^{1}}}-{\frac {\n}\cdot \}-{\frac {\n}\frac {d}n}{\mathrmath {d}}}}}}}}\rigda \right).}.}.}.}$

매질이 관찰자를 향해 또는 멀리로 흐르기 때문에 매체를 통해 이동하는 빛은 도플러-시프트(Doppler-Shift)이며, 공식에 사용되는 굴절률(Rubtible)은 도플러-시프트 파장에 그만큼 적합해야 한다.^{[P 3]}지만은 1915년에 로렌츠 분산 용어의 존재를 확인했다.^{[P 4]}

프레넬의 드래그 계수는 실제로 상대론적 속도 추가 공식에 따른다는 것이 나중에 밝혀졌다. 특수 상대성에서의 파생 섹션을 참조하라.

반복

앨버트 A.마이켈슨과 에드워드 W. 몰리, 프랑스의 물리학자의 원래 실험:(1)프랑스의 물리학자의 장치의 광학 구성 요소의 내력 및 변형 성상;그 물의 가압 흐름만 쉬 지속되었다(2)관찰, 이송되었다artifactual 프린지 변위를 일으킬 수 없는 여러 우려를 해결해 개선된 정확하게 프랑스의 물리학자의 실험 반복(1886년)[P5].찌꺼기(3) 피조의 작은 직경 튜브를 통과하는 물의 층류 흐름 프로필은 중심 부분만 사용할 수 있어 희미한 프링(fring)이 발생한다는 것을 의미했다. (4) 관 직경의 유량에 대한 피조의 결정에 불확실성이 있었다.Michelson은 3분 동안 일정한 물의 흐름을 제공하는 더 큰 직경의 튜브와 큰 저장고를 가지고 Fizeau의 장비를 재설계했다.그의 공통 경로 간섭계 설계는 경로 길이의 자동 보정을 제공함으로써 광학적 요소가 정렬되는 즉시 흰색 광선 프링(fring)을 한 번에 볼 수 있도록 했다.지형학적으로 빛 경로는 각 빛 경로에서 반사의 수가 짝수인 Sagnac 간섭계의 경로였다.^{[S 4]}이것은 아주 안정적인 프링들을 제공했는데, 첫째 순서는 그것의 광학 구성 요소의 어떠한 움직임에도 완전히 무감각한 것이었다.그 안정성은 그가 h에 유리판을 삽입하거나 심지어 프린지 계통의 중심을 바꾸지 않고 빛길에서 불을 밝힌 성냥을 들고 있을 수 있을 정도로 가능했다.이 기구를 이용해 미켈슨과 몰리는 물속뿐만 아니라 공중에서도 피조의 결과를 완전히 확인할 수 있었다.^{[P 5]}

다른 실험들은 1914-1915년에 피터 지만에 의해 수행되었다.지만은 암스테르담의 주 수도관에 직접 연결된 미켈슨 기구의 스케일업 버전을 사용하여 보라색(4358 å)부터 적색(6870 å)^{[P 6][P 4]}에 이르는 단색광을 사용하여 확장 측정을 수행하여 로렌츠의 변형 계수를 확인할 수 있었다.1910년에 프란츠 하레스는 회전장치를 사용했고 전체적으로 프레넬의 드래그 계수를 확인했다.그러나 그는 데이터에서 추가로 "체계적 편향"을 발견했고, 이는 나중에 Sagnac 효과로 밝혀졌다.^{[S 5]}

그 이후로 굴절률이 다른 다양한 재료에서 그러한 끌기 계수를 측정하는 많은 실험이 종종 Sagnac 효과와 결합하여 수행되었다.^{[S 6]}예를 들어 회전 디스크와 함께 링 레이저를 사용하는 실험이나 중성자 간섭계 실험에서 그렇다.^{[P 7][P 8][P 9][P 10][P 11][P 12][P 13]}또한 가로 방향 끌기 효과가 관찰되었다. 즉, 매개체가 입사광의 방향에 직각으로 움직이고 있을 때 말이다.^{[P 3][P 14]}

호크 실험

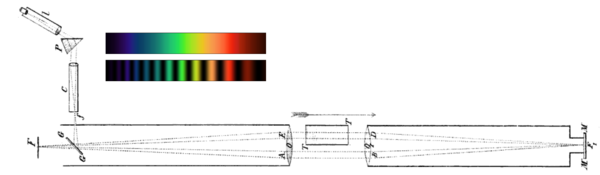
프레스넬의 드래그 계수에 대한 간접적인 확인은 마틴 호크(1868년)에 의해 제공되었다.^{[P 15][S 7]}그의 기구는 피조의 것과 비슷했지만, 그의 버전에서는 오직 한 팔만이 휴식수로 채워진 영역을 포함하고 있었고, 다른 팔은 공중에 있었다.에테르 안에서 쉬고 있는 관찰자에게서 보듯이 지구와 물이 움직이고 있다.따라서 두 광선이 반대 방향으로 이동하는 다음 이동 시간은 호크(횡방향은 무시한 채 이미지 참조)에 의해 계산되었다.

${\displaystyle t_{1}={\frac {AB}{c+v}+{\frac {DE}{{\frac {c}{n}-v}\,}$ ${\displaystyle t_{2}={\frac {AB}{c-v}+{\frac {DE}{{\frac {c}{n}+v}\ .}$

그림 6.Hoek은 관측된 스펙트럼이 에테르 바람을 가로지르는 기구에 연속적으로 작용하고, 바람과 평행한 기구에 띠를 두길 기대했다.실제 실험에서 그는 악기의 방향과 상관없이 밴딩이 없는 것을 관찰했다.

이동 시간은 동일하지 않으며, 간섭 시프트로 표시해야 한다.그러나 에테르 프레임의 물에 프레스넬의 드래그 계수를 적용하면 이동 시간 차이(v/c의 첫 번째 순서)가 사라진다.다른 설정을 사용하여 Hoek는 실제로 null 결과를 얻어 Freshnel의 드래그 계수를 확인했다. (에테르 바람을 차단할 가능성을 반박하는 유사한 실험의 경우 Hammar 실험을 참조한다.)

여기에 제시된 실험의 특정 버전에서 호크는 프리즘 P를 사용하여 슬릿의 빛을 시준기 C를 통과한 스펙트럼으로 분산시켜 기구에 진입했다.가상의 에테르 바람과 평행한 기구를 가진 Hoek은 한 회로의 빛이 다른 회로에 대해 7/600 mm 지연될 것으로 예상했다.이 지연이 파장의 정수인 경우, 그는 건설적인 간섭을 볼 것으로 기대했고, 이 지연이 절반의 정수인 파장을 나타내는 경우 파괴적인 간섭을 볼 것으로 기대했다.끌지 않는 경우, 관측된 스펙트럼이 에테르 바람에 횡방향으로 향하는 기기와 연속되고 에테르 바람과 평행한 기기와 띠를 이루기를 기대했다.그의 실제 실험 결과는 완전히 부정적이었다.^{[P 15][S 7]}

논란

Although Fresnel's hypothesis was empirically successful in explaining Fizeau's results, many leading experts in the field, including Fizeau himself (1851), Éleuthère Mascart (1872), Ketteler (1873), Veltmann (1873), and Lorentz (1886) were united in considering Fresnel's partial aether-dragging hypothesis to be on shaky theoretical grounds.예를 들어, 벨트만(1870)은 프레스넬의 공식은 굴절 지수가 파장에 따라 다르기 때문에 다른 색상의 빛에 대해 에테르를 다른 양만큼 끌어야 한다는 것을 의미한다고 설명했고, 마스카르트(1872)는 이환성 매체를 통해 이동하는 편광에 대해서도 비슷한 결과를 보여주었다.즉, 에테르는 동시에 다른 동작을 유지할 수 있어야 한다.^{[S 8]}

Fizau는 자신의 실험 결과에 대한 불만족을 그의 보고서에 대한 결론에서 쉽게 알아차린다.

실험의 성공은 프레넬의 가설을 채택하는 데 필요한 것으로 보인다. 또는 적어도 신체의 움직임의 효과에 의한 빛의 속도의 변화를 표현하기 위해 그가 발견한 법칙을 제시해 주는 것으로 보인다. 비록 그 법칙이 사실이라고 밝혀지기는 하지만, 그것은 단지 하나의 공동에 불과한 가설에 대한 매우 강력한 증거가 될 수 있기 때문이다.nsequence, 아마도 프레스넬의 개념은 그렇게 비범하게 보일지도 모르고, 어떤 면에서는 너무나 어려운 점에서는, 그 사건의 실체적 사실의 표현으로 채택하기 전에 다른 증거와 기하학적 측면에 대한 심오한 검토가 여전히 필요할지도 모른다.^{[P 1]}

프레스넬의 부분적인 에테르끌기 가설에 대한 대부분의 물리학자들의 불만에도 불구하고, 다른 사람들에 의한 피조의 실험(위 섹션 참조)에 대한 반복과 개선은 그의 결과를 높은 정확도로 확인시켜 주었다.

부분적인 에테르끌기 가설의 문제 외에도 미셸슨-몰리 실험(1887년)과 함께 또 하나의 큰 문제가 발생했다.프레스넬의 이론에서는 에테르가 거의 정지해 있고 그 사이로 지구가 움직이고 있기 때문에 그 실험은 긍정적인 결과를 주었어야 했다.그러나 이 실험의 결과는 부정적이었다.따라서 당시 에테르 모델의 관점에서 보면 실험 상황은 모순되었다.한편으로 1886년 미켈슨과 몰리에 의한 빛의 일탈, 피조 실험과 그 반복은 약간의 에테르 드레이그만 지지하는 것으로 보였다.한편, 1887년의 미셸슨-몰리 실험은 에테르가 지구와 관련하여 쉬고 있다는 것을 증명하는 것으로 나타나, 에테르 드레이깅의 완전한 사상을 지지하는 것으로 보인다(에테르 드래그 가설 참조).^{[S 9]}그래서 피조의 결과를 설명하는 데 프레스넬의 가설의 바로 그 성공은 이론적 위기로까지 이어졌는데, 이는 특수상대성이론의 발전이 있기 전까지는 해결되지 않았다.^{[S 8]}

로렌츠의 해석

1892년 헨드릭 로렌츠는 에테르가 완전히 정지해 있는 프레스넬의 모델의 수정을 제안했다.그는 드래그되지 않은 에테르와 움직이는 물 사이의 상호작용의 결과로 프레스넬의 드래그 계수를 도출하는 데 성공했다.^{[S 9][S 10]: 25–30} 그는 또한 한 기준 프레임에서 다른 기준 프레임으로의 전환을 현지 시간이라고 부르는 보조 시간 변수를 사용하여 단순화할 수 있다는 것을 발견했다.

${\displaystyle t^{\prime }=t-{\frac {frac}{c^{2}}}\ .}$

1895년에 로렌츠는 보다 일반적으로 현지 시간의 개념을 바탕으로 프레스넬의 계수를 설명했다.그러나 로렌츠의 이론은 프레스넬의 이론과 같은 근본적인 문제를 가지고 있었다: 정지된 에테르가 미셸슨-몰리 실험과 모순된다.그래서 1892년 로렌츠는 움직이는 신체가 운동의 방향으로 수축할 것을 제안했다(조지 피츠제럴드가 이미 1889년에 이 결론에 도달했기 때문에 피츠제랄드-로렌츠 수축 가설).그가 이러한 효과를 설명하기 위해 사용한 방정식은 1904년까지 그에 의해 더욱 발전되었다.이것들은 이제 그를 기리는 로렌츠 변형이라고 불리며, 아인슈타인이 나중에 첫 번째 원칙에서 도출한 방정식과 형태는 동일하다.그러나 아인슈타인의 방정식과는 달리 로렌츠의 변신은 철저히 임시방편적이었으며, 그들의 유일한 정당성은 효과가 있는 것 같다는 것이었다.^{[S 9][S 10]: 27–30}

특수상대성에서의 파생

아인슈타인은 로렌츠의 방정식이 어떻게 두 개의 단순한 출발 체계의 논리적인 결과로 도출될 수 있는지를 보여주었다.게다가 아인슈타인은 정지된 에테르 개념은 특수상대성이론에서 설 자리가 없으며 로렌츠 변환은 공간과 시간의 본질과 관련이 있다는 것을 인식했다.움직이는 자석과 도체 문제, 음의 에테르 표류 실험, 빛의 일탈과 함께 피조 실험은 아인슈타인의 상대성에 대한 생각을 형성한 중요한 실험 결과 중 하나였다.^{[S 11][S 12]}로버트 S. 샨클랜드는 아인슈타인과 몇 가지 대화를 보도했는데, 아인슈타인은 피조 실험의 중요성을 강조했다.^{[S 13]}

그는 자신에게 가장 큰 영향을 준 실험 결과는 항성 일탈의 관측과 움직이는 물에서 빛의 속도에 대한 피조의 측정이라고 계속해서 말했다."그들은 충분했다"고 그는 말했다.

Max von Laue(1907)는 프레스넬 드래그 계수가 속도의 추가를 위한 상대론적 공식의 자연적 결과로서 쉽게 설명될 수 있음을 입증했다.^{[S 14]} 즉, 다음과 같다.

움직이지 않는 물에서 빛의 속도는 c/n이다.

속도 조성법에서는 물이 (빛과 같은 방향으로) 속도 v와 함께 흐르는 실험실에서 관찰된 빛의 속도가 다음과 같은 것을 따른다.

${\displaystyle V_{\mathrm {lab}}}}={\frac {{\frac{c}{n}{n}{c^{n}{{n}}}}}}={\frac {{\frac {{n}{n}}}}{1+{v}}}}{cn}}}}}}}}}}}}}}}}}}}}}}}}}.$

따라서 속도 차이는 다음과 같다(v가 c에 비해 작다고 가정하고 더 높은 주문 조건을 떨어뜨림).

${\displaystyle V_{\mathrm {lab} }-{\frac {c}{n}}={\frac {{\frac {c}{n}}+v}{1+{\frac {v}{cn}}}}-{\frac {c}{n}}={\frac {{\frac {c}{n}}+v-{\frac {c}{n}}(1+{\frac {v}{cn}})}{1+{\frac {v}{cn}}}}}$ ${\displaystyle ={\frac {1}{n^{2}}\\오른쪽)}{1+{\frac {v}{v}}}}}}}}{1-{\frac {1}{n^}\오른쪽)\.}$

이는 v/c 1 1일 때 정확하며, v/c ≪ 1 조건을 만족한 Fizau의 측정에 기초한 공식에 동의한다.

따라서 Fizau의 실험은 아인슈타인의 속도 첨가 공식의 시준 케이스에 대한 증거를 뒷받침하고 있다.^{[P 16]}

참고 항목

• 특수상대성 검정
• 에테르 드래그 가설
• 특수상대성이론의 역사

참조

이차 출처

일차 출처