케네디–손다이크 실험

더 케네디– 1932년 로이 J. 케네디와 에드워드 M.이 처음으로 실시한 손다이크 실험. Thorndike는 특수 상대성 이론을 테스트하는 마이컬슨-몰리 실험 절차의 수정된 형태입니다.^[1] 수정된 것은 고전적인 마이컬슨-몰리(MM) 장치의 한쪽 팔을 다른 한쪽 팔보다 더 짧게 만드는 것입니다. 마이컬슨-몰리 실험은 빛의 속도가 장치의 방향과 무관하다는 것을 보여주었지만, 케네디는–손다이크 실험은 다양한 관성 프레임에서 장치의 속도와도 무관함을 보여주었습니다. 그것은 시간 확장을 간접적으로 확인하는 테스트로도 사용되었습니다 – 마이컬슨-몰리 실험의 부정적인 결과는 길이 수축만으로 설명할 수 있지만, 케네디의 부정적인 결과입니다.–손다이크 실험은 지구가 태양 주위를 도는 동안 위상 변화가 감지되지 않는 이유를 설명하기 위해 길이 수축 외에 시간 확장이 필요합니다. 시간 확장에 대한 최초의 직접적인 확인은 Ives-Stilwell 실험에 의해 달성되었습니다. 이 세 가지 실험의 결과를 종합하면 완전한 로렌츠 변환을 유도할 수 있습니다.^[2]

케네디의 개량형–광학 공동 또는 Lunar Laser Ranging을 사용하여 Thorndike 실험을 수행했습니다. 로렌츠 불변성 검정의 일반적인 개요는 특수 상대성 검정을 참조하십시오.

실험이

원래 마이컬슨-몰리 실험은 로렌츠-피츠 제럴드 수축 가설을 검정하는 데만 유용했습니다. 케네디는 이미 1920년대에 MM 실험의 점점 더 정교한 버전을 여러 번 만들어보았는데, 그 때 그는 시간 확장을 실험하는 방법도 생각해 냈습니다. 그들 자신의 말로 표현하면:^[1]

이 실험의 기초가 되는 원리는 균일한 빛의 빔이 두 개의 빔으로 분할되어 서로 다른 길이의 경로를 통과한 후 다시 합쳐지면 빛의 주파수가 […]에 의존하지 않는 한 상대적인 위상은 장치의 속도에 따라 […]에 의존할 것이라는 간단한 제안입니다.] 상대성 이론에 의해 요구되는 방식의 속도에 대해.

그림 1을 참조하면, 주요 광학 구성 요소는 매우 낮은 열 팽창 계수의 융합된 석영 기반 위에 진공 챔버 V 내에 장착되었습니다. 워터재킷 W는 온도를 0.001 °C 이내로 조절했습니다. 수은원 Hg의 단색 녹색 빛은 진공 챔버에 들어가기 전에 니콜 편광 프리즘 N을 통과하고, 원하지 않는 후면 반사를 방지하기 위해 브루스터 각도로 설정된 빔 스플리터 B에 의해 분리되었습니다. 두 빔은 5461Å 수은선(≈32cm, 팔 길이 δ16cm)의 가간섭성 길이를 감안할 때 가능한 한 거리를 달리하여 설정된 두 개의 거울 M과 M을 향했습니다. 반사된 빔들은 재결합하여 원형 간섭무늬를 형성하였고, 이는 P에서 촬영되었습니다. 슬릿 S를 사용하면 하루 중 다른 시간에 링의 직경을 가로지르는 여러 노출을 하나의 사진판에 기록할 수 있습니다.

실험의 한 팔을 다른 팔보다 훨씬 짧게 함으로써, 지구의 속도 변화는 광선의 이동 시간에 변화를 일으킬 것이고, 광원의 진동수가 같은 정도로 변하지 않는 한 그로부터 가장자리 이동을 초래할 것입니다. 이와 같은 프린지 시프트가 발생했는지를 확인하기 위해 간섭계를 매우 안정적으로 만들고 간섭 패턴을 촬영하여 나중에 비교하였습니다. 테스트는 여러 달에 걸쳐 수행되었습니다. (오차 범위 내에서 10±10 km/s의 속도에 해당하는) 중요한 가장자리 이동이 발견되지 않았기 때문에, 실험자들은 특수 상대성 이론에 의해 예측된 대로 시간 확장이 발생한다고 결론지었습니다.

이론.

실험의 기본이론

로렌츠-피츠 제럴드 수축(로렌츠 수축) 자체로는 마이컬슨-몰리 실험의 귀무 결과를 충분히 설명할 수 있지만, 케네디의 귀무 결과를 설명할 수는 없습니다.–손다이크 실험. 로런츠-피츠 제럴드 수축은 다음 공식으로 주어집니다.

${\displaystyle L=L_{0}{\sqrt {1-v^{2}/c^{2}}}=L_{0}/{\gamma (v)}}$

어디에

${\displaystyle {L0\mathrm{}}_{}}$ ${\$는 적절한 길이(휴면 프레임에 있는 개체의 길이)이며,

${\displaystyle L}$ ${\displaystyle L}$은 물체에 대한 상대 운동에서 관찰자가 관찰한 길이입니다.

${\displaystyle v}$ ${\$은 관찰자와 이동하는 물체 사이의 상대 속도, 즉 가상 에테르와 이동하는 물체 사이의 상대 속도입니다.

$c {\$ c$\,}$는 빛의 속도입니다.

로런츠 인자는 다음과 같이 정의됩니다.

$)$ ≡ $11$ - v 2 / c 2 {\displaysty${\displaystyle \mathrm{le\; \backslash g}}$amma (v)\equiv {\frac {1}{\sqrt {1-v^{2}/c^{2}}}\}.

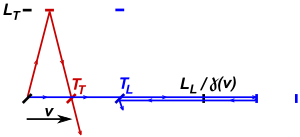
그림 2는 케네디를 보여줍니다.–직각 암을 가진 Thorndike 장치로 로렌츠 수축의 유효성을 가정합니다.^[3] 장치가 가상 에테르에 대해 움직이지 않는 경우, 빛이 종방향 및 횡방향 암을 통과하는 데 걸리는 시간 차이는 다음과 같습니다.

${\displaystyle T_{L}-T_{T}={\frac {2(L_{L}-L_{T})}{c}}}$

로런츠 수축 길이를 따라 빛이 왕복하는 데 걸리는 시간은 다음과 같습니다.

${\displaystyle T_{L}=T_{1}+T_{2}={\frac {L_{L}/\gamma (v)}{c-v}}+{\frac {L_{L}/\gamma (v)}{c+v}}={\frac {2L_{L}/\gamma (v)}{c}}{\frac {1}{1-{\frac {v^{2}}{c^{2}}}}}={\frac {2L_{L}\gamma (v)}{c}}}$

여기서 T는₁ 운동 방향의 이동 시간, T는₂ 반대 방향, v는 발광 에테르에 대한 속도 성분, c는 빛의 속도, L은_L 종간 간섭계 암의 길이입니다. 빛이 가로 팔을 가로질러 뒤로 이동하는 데 걸리는 시간은 다음과 같습니다.

${\displaystyle T_{T}={\frac {2L_{T}}{\sqrt {c^{2}-v^{2}}}}={\frac {2L_{T}}{c}}{\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}={\frac {2L_{T}\gamma (v)}{c}}}$

빛이 종방향 암과 횡방향 암을 통과하는 데 걸리는 시간의 차이는 다음과 같습니다.

${\displaystyle T_{L}-T_{T}={\frac {2(L_{L}-L_{T})\gamma (v)}{c}}}$

δL=c(T-T)이기 때문에 다음과 같은 주행 길이 차이가 있습니다(δL은 초기 주행 길이 차이이고 v는 장치의 초기 속도이며, δL과 v는 지구 자체의 자전 또는 태양 주위의 자전으로 인한 회전 또는 속도 변화 후).

${\displaystyle \Delta L_{A}={\frac {2\left(L_{L}-L_{T}\right)}{\sqrt {1-v_{A}^{2}/c^{2}}}},\qquad \Delta L_{B}={\frac {2\left(L_{L}-L_{T}\right)}{\sqrt {1-v_{B}^{2}/c^{2}}}}}$.

부정적인 결과를 얻기 위해서는 δL- δL= 0이 있어야 합니다. 그러나 두 공식 모두 속도가 동일한 경우(v=v)에서만 서로 상쇄되는 것을 알 수 있습니다. 그러나 속도가 다르다면 δL과 δL은 더 이상 동일하지 않습니다. (Michelson-Morley 실험은 L과_L L의_T 차이가 0이기 때문에 속도 변화에 영향을 받지 않습니다. 따라서 MM 실험에서는 광속이 장치의 방향에 따라 달라지는지 여부만 테스트합니다.) 하지만 케네디에서–손다이크 실험, 처음부터_L 길이 L과 L이_T 다르므로 광속이 장치의 속도에 미치는 의존성을 측정할 수도 있습니다.^[2]

이전 공식에 따르면 주행 길이 차이 δ-δ-δL과 결과적으로 예상되는 프린지 시프트 λN은 다음과 같이 표시됩니다(λ는 파장).

${\displaystyle \Delta N={\frac {\Delta L_{A}-\Delta L_{B}}{\lambda }}={\frac {2\left(L_{L}-L_{T}\right)}{\lambda }}\left({\frac {1}{\sqrt {1-v_{A}^{2}/c^{2}}}}-{\frac {1}{\sqrt$${1-v_{B}^{2}/c^{2}}}}\right)}$.

v/c의 2차 이상 크기 무시:

${\displaystyle \approx {\frac {L_{L}-L_{T}}{\lambda }}\left({\frac {v_{A}^{2}-v_{B}^{2}}{c^{2}}}\right)}$

일정한 δN, 즉 프린지 시프트가 장치의 속도 또는 방향과 독립적이기 위해서는 주파수 및 따라서 파장 λ이 로렌츠 계수에 의해 수정되어야 합니다. 주파수에 대한 시간 확장의 영향을 고려할 때 실제로 그렇습니다. 따라서 케네디의 부정적인 결과를 설명하기 위해서는 길이 수축과 시간 확장이 모두 필요합니다.–손다이크 실험.

상대성의 중요성

1905년, 앙리 푸앵카레와 알베르트 아인슈타인에 의해 로렌츠 변환이 상대성 원리를 만족시키기 위해 집단을 형성해야 한다는 것이 밝혀졌습니다(로렌츠 변환의 역사 참조). 이를 위해서는 길이 수축과 시간 팽창이 정확한 상대론적 값을 가져야 합니다. 이제 케네디와 손다이크는 마이컬슨-몰리 실험과 케네디의 실험 데이터로부터 완전한 로런츠 변환을 이끌어낼 수 있다고 주장했습니다.–손다이크 실험. 그러나 정확한 상대론적 값을 갖는 길이 수축과 시간 확장은 두 실험의 설명에 충분하지만 필요하지 않기 때문에 이것은 엄격하게 정확하지 않습니다. 왜냐하면 오직 운동 방향으로의 길이 수축만이 마이컬슨-몰리 실험을 설명할 수 있는 하나의 가능성이기 때문입니다. 일반적으로 귀무 결과는 가로 길이와 세로 길이 사이의 비율이 로렌츠 계수와 일치해야 합니다. 여기에는 가로 방향과 세로 방향의 길이 변화의 조합이 무한히 많이 포함됩니다. 이것은 케네디에서의 시간 확장의 역할에도 영향을 미칩니다.–손다이크 실험, 그 값은 실험의 분석에 사용된 길이 수축 값에 따라 달라지기 때문입니다. 따라서 실험 데이터만으로 로렌츠 변환을 도출하기 위해서는 세 번째 실험인 Ives-Stilwell 실험을 고려할 필요가 있습니다.^[2]

더 정확하게: Robertson-Mansouri-Sexl 검정 이론의 틀에서 실험을 설명하기 위해 다음과 같은 체계가 사용될 수 있습니다: α는 시간 변화를 나타내고, β 길이는 운동 방향으로, δ 길이는 운동 방향에 수직으로 변화합니다. 마이컬슨-몰리 실험은 β와 δ의 관계를 검정하는 반면 케네디는–손다이크 실험은 α와 β의 관계를 검정합니다. 따라서 α는 β 자체에 의존하는 δ에 의존하며, 이 두 실험에서는 그 양들의 조합만 측정할 수 있고 개별 값은 측정할 수 없습니다. 이러한 양 중 하나의 값을 직접 측정하기 위해서는 또 다른 실험이 필요합니다. 이것은 실제로 상대론적 시간 팽창에 의해 예측된 값을 갖는 것으로 α를 측정한 Ives-Stilwell 실험으로 달성되었습니다. 이 값을 케네디와 결합합니다.–손다이크 귀무 결과는 β가 반드시 상대론적 길이 수축의 값을 가정해야 함을 보여줍니다. 그리고 β에 대한 이 값을 마이컬슨-몰리 귀무 결과와 결합하면 δ이 0이어야 함을 알 수 있습니다. 그래서 로렌츠 변환에 필요한 구성 요소는 군 이론의 이론적 요구 사항과 일치하는 실험에 의해 제공됩니다.

최근 실험

캐비티 테스트

최근 몇 년간, 케네디 뿐만 아니라 마이컬슨-몰리 실험.–레이저, 마스터, 극저온 광공진기를 이용하여 정밀도를 높인 손다이크형 실험이 반복되었습니다. 시간 확장과 길이 수축 사이의 관계를 나타내는 로버트슨-만수리-섹슬 테스트 이론(RMS)에 따른 속도 의존성의 한계가 크게 개선되었습니다. 예를 들어, 원래 케네디는–손다이크 실험은 RMS 속도 의존성에 대한 한계를 ~10으로⁻² 설정했지만 전류 한계는 ~10⁻⁸ 범위에 있습니다.^[5]

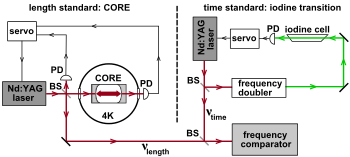
그림 3은 2002년 브랙스마이어 등이 케네디를 반복한 것을 간략하게 도식화한 것입니다.–손다이크 실험.^[6] 왼쪽의 광검출기(PD)는 액체 헬륨 온도에서 유지되는 사파이어 극저온 광 공진기(CORE) 길이 표준의 공진을 모니터링하여 다음과 같은 주파수를 안정화합니다.YAG 레이저에서 1064nm까지입니다. 오른쪽에는 저압 요오드 기준의 532nm 흡광도 라인이 시간 표준으로 사용되어 두 번째 Nd의 (2배) 주파수를 안정화합니다.야그 레이저.

작가.	연도	묘사	최대 속도 의존성
힐스 앤[7] 홀	1990	광학 Fabry-Pérot 공동의 주파수와 I2 기준선에 안정화된 레이저의 주파수를 비교합니다.	${\displaystyle \lesssim 10^{-5}}$
Braxmaier et al.[6]	2002	두 Nd를 사용하여 극저온 광 공진기의 주파수를 I2 주파수 표준과 비교:YAG 레이저.
늑대 등.[8]	2003	귓속말 갤러리 모드로 작동하는 사파이어 결정으로 구성된 정지형 극저온 마이크로파 발진기의 주파수는 세슘과 루비듐 원자 분수 시계와 비교되는 수소 마커와 비교됩니다. 지구가 자전하는 동안의 변화를 찾아왔습니다. 2001-2002년 사이의 자료를 분석하였습니다.	${\displaystyle \lesssim 10^{-7}}$
늑대 등.[9]	2004	울프 등 참조. (2003). 능동적인 온도 제어를 구현했습니다. 2002-2003년 사이의 자료를 분석하였습니다.
토바 등.[10]	2009	울프 등 참조. (2003). 2002-2008년 사이의 데이터는 실제 및 연간 변동 모두에 대해 분석되었습니다.	${\displaystyle \lesssim 10^{-8}}$

달 레이저 거리 측정

지상 측정 외에 케네디–Thorndike 실험은 Lunar Laser Ranging 데이터를 사용하여 Müller & Soffel(1995)^[11]과 Müller et al.(1999)^[12]에 의해 수행되었으며, 여기서 지구-달 거리는 센티미터의 정확도로 평가됩니다. 선호하는 기준 프레임이 있고 빛의 속도가 관찰자의 속도에 따라 달라지는 경우 지구-달 거리 측정에서 비정상적인 진동을 관찰할 수 있어야 합니다. 시간 확장은 이미 높은 정밀도로 확인되었기 때문에 이러한 진동의 관찰은 관찰자의 속도에 대한 빛의 속도의 의존성과 길이 수축의 방향 의존성을 보여줄 것입니다. 그러나 Hils and Hall(1990)에 의해 설정된 경계와 유사한 ~^[12]10의⁻⁵ RMS 속도 경계를 갖는 이러한 진동은 어느 연구에서도 관찰되지 않았습니다. 따라서 길이 수축과 시간 팽창 모두 상대성 이론에 의해 예측된 값을 가져야 합니다.

참고문헌