말했다

스포크는 휠(축이 연결되는 허브)의 중심에서 방사되는 일부 로드 중 하나로, 허브와 둥근 트랙션 표면을 연결합니다.

테헤란에 있는 이란 국립 박물관에 전시된 스포크 바퀴.그 바퀴는 기원전 2천년 후반으로 거슬러 올라가며 초카 잔빌에서 발굴되었다.

금속 액슬 어셈블리가 있는 카트 휠 한 쌍의 잔여물.

남아프리카공화국 알리월 북부에 있는 왜건입니다.스포크 3개가 없어지고 금속 타이어가 있는 것을 확인합니다.

골동품 트럭의 금속 테두리가 달린 나무 스포크 휠이 지하 애틀랜타에 전시되어 있습니다.

자전거의 금속 장력 스포크 휠.

이 용어는 원래 로그에서 4개 또는 6개의 섹션으로 분할된 부분을 가리킵니다.수레바퀴의 방사형 부재는 통나무를 깎아 완성된 모양으로 만들었다.스포크쇼는 원래 이 목적을 위해 개발된 도구입니다.결국, 스포크라는 용어는 그들이 사용한 재료보다 휠라이트 작품의 완제품에 더 일반적으로 적용되었다.

역사

스포크가 달린 바퀴는 가볍고 빠른 차량을 만들기 위해 발명되었다.스포크 바퀴에 대한 최초의 물리적 증거는 기원전 ^[1]2000년으로 거슬러 올라가는 신타슈타 문화에서 발견되었다.그 직후, 코카서스 지역의 말 문화는 3세기 동안 말이 끄는 바퀴 달린 전차를 사용했다.그들은 그리스 반도 깊숙이 이주하여, 기존의 지중해 민족들과 합류했고, 결국 고전주의 이전의 스파르타와 아테네가 이끈 미노아의 지배와 통합이 깨진 후에 고전 그리스가 탄생했다.

치바르 눌라, 차투르 보즈 나트 눌라, 카토티아 등 인도 각지의 신찰콜리스주의/원고사기(기원전 ^{[note 1]}제2천년기) 그림은 바퀴가 ^[5]달린 병거의 사용을 묘사하고 있다.

켈트족 전차는 기원전 1천년에 바퀴 주위에 철제 테두리를 도입했다.스포크 휠은 와이어 휠과 고무 타이어가 ^[6]발명된 1870년대까지 큰 수정 없이 계속 사용되었습니다.

건설

스포크는 장력 또는 압축 여부에 따라 목재, 금속 또는 합성 섬유로 만들 수 있습니다.

압축 스포크

나무 스포크가 달린 바퀴의 원래 형태는 말이 끄는 마차나 마차에 사용되었다.초기 자동차에서는 포병형 나무 바퀴가 일반적으로 사용되었다.

단순한 나무 바퀴는 허브에 가해지는 부하로 인해 가장 낮은 나무 스포크가 짧아지고 압축될 때 바퀴 림은 지면에 약간 평평해집니다.다른 나무 스포크들은 큰 변화를 보이지 않는다.

나무 스포크는 방사형으로 장착되어 있습니다.또한 흔들림을 방지하기 위해 일반적으로 차량 외부로 분리됩니다.또한 디싱을 통해 ^[7]더 많은 디싱을 통해 흡수된 습기로 인한 스포크의 팽창을 휠이 보상할 수 있습니다.

텐션 스포크

자전거에 사용하기 위해, 무거운 나무 바퀴는 와이어 휠이라고 불리는 팽팽하고 조절 가능한 금속 와이어로 만들어진 스포크를 가진 가벼운 바퀴로 대체되었다.이것들은 휠체어, 오토바이, 자동차, 그리고 초기 항공기에도 사용된다.

종류들

일부 유형의 휠에는 분리 가능한 스포크가 있어 파손되거나 구부러질 경우 개별적으로 교체할 수 있습니다.여기에는 자전거와 휠체어 바퀴가 포함됩니다.일반적인 바퀴를 가진 고품질 자전거는 스테인리스 스틸 스포크를 사용하는 반면, 저렴한 자전거는 아연도금(녹슬지 않음) 또는 크롬 도금 스포크를 사용할 수 있습니다.좋은 품질의 스포크는 약 225kgf(c. 500파운드 힘 또는 2,200뉴턴)의 장력을 지탱할 수 있지만 피로 장애를 피하기 위해 이 하중의 극히 일부에서 사용됩니다.자전거와 휠체어 바퀴 스포크는 장력만 있기 때문에 합성 섬유와 같은 유연하고 강한 소재도 가끔 사용됩니다.^[8]금속 스포크는 공기역학적 저항을 줄이기 위해 타원형 또는 블레이드를 사용할 수 있으며, 강도를 유지하면서 무게를 줄이기 위해 버팅(두 배 또는 세 배)할 수도 있습니다.

와이어 스포크 휠의 변형은 티오가의 "텐션 디스크"로 표면적으로는 솔리드 디스크로 보이지만 실제로는 일반적인 텐션 스포크 휠과 동일한 원리를 사용하여 제작되었습니다.개별 와이어 스포크 대신 연속된 케블라(아라미드) 실을 사용하여 높은 장력 하에서 허브와 림 사이의 끈을 묶었습니다.나사산은 보호 및 공기역학적 이점을 위해 반투명 디스크에 포장되어 있었지만 구조적인 구성요소는 아니었습니다.

통상의 스포크^[9] 직경

와이어 게이지	직경	단면적
15G	1.8 mm	3.24mm²
14G	2.0 mm	4 mm²
13G	2.3 mm	5.29mm²
12세대	2.6 mm	6.76 mm²
제11세대	2.9 mm	8.41 mm²
10G	3.2 mm	10.24 mm²

접선 레이싱

와이어 스포크는 허브에 방사상으로 장착될 수 있지만 허브에 접선 방향으로 장착되는 경우가 많습니다.접선 스포킹은 림과 허브 사이의 토크 전달을 가능하게 합니다.따라서 접선 스포크는 페달링으로부터 허브에 토크가 있는 구동 휠과 제동 시 (허브를 통해) 림에서 브레이크로 토크를 전달하는 디스크 또는 밴드 브레이크와 같은 허브 장착 브레이크를 사용하는 모든 휠에 필요합니다.

휠빌딩

구성 부품으로 장력 스포크 휠을 구성하는 것을 휠빌딩이라고 하며, 견고하고 오래 지속되는 최종 제품을 위한 올바른 제작 절차가 필요합니다.텐션 스포크는 보통 림 또는 때로는 스포크 니플이 있는 허브에 부착됩니다.다른 한쪽 끝은 일반적으로 디스크에 끼워지거나 허브의 구멍을 통해 당겨지지 않도록 하기 위해 "Z"로 구부려집니다.구부러진 버전은 리어 기어를 탈거하지 않고도 리어 자전거 휠의 부러진 스포크를 교체할 수 있는 장점이 있습니다.

중량 대 강도 비율이 뛰어난 와이어 휠은 곧 경차용으로 인기를 끌었다.일반 자동차에서 와이어 휠은 곧 저렴한 금속 디스크 휠로 대체되었지만 와이어 휠은 1960년대까지 스포츠 카에서 인기를 끌었다.스포크 바퀴는 여전히 오토바이와 자전거에서 인기가 있다.

스포크 길이

자전거 바퀴를 제작할 때는 스포크의 길이가 정확해야 합니다. 그렇지 않으면 나사산이 충분히 맞물리지 않아 휠이 약해지거나 림을 통해 돌출되어 내부 튜브에 구멍이 날 수 있습니다.

계산

자전거 스포크의 경우, 스포크 길이는 플랜지 시트에서 나사산 팁까지 정의됩니다.끝이 구부러진 스포크의 경우 공칭 스포크 길이에 구부러진 끝의 스포크 폭은 포함되지 않습니다.

(표준인) 스포크가 교차하는 휠의 경우 바람직한 스포크 길이는

l=sqrt {d^{2}+{r_{1}^2}+{r_{2}-2,r_{1}r_{2}\cos(a)}-r_{3}

어디에

d = 허브 중심(축을 따라)에서 플랜지까지의 거리(예: 30 mm,
r₁ = 허브의 스포크 홀 원 반지름(예: 19.5 mm),
r₂ = 유효 림 직경(ERD)의 절반 또는 스포크 끝의 직경(이 문서에 첨부된 '설명' 참조), 예를 들어 301mm,
r₃ = 플랜지에 있는 스포크 구멍의 반지름(예: 1.1 mm),
m = 휠의 한쪽에 사용할 스포크 수(예: 36/2=18),
k = 스포크당 크로스 수(예: 3 및
a = 360°k/m(예: 360°*3/18 = 60°)

d에 대하여: 디스크 브레이크가 없는 프론트 휠과 같은 대칭 휠의 경우 플랜지 간 거리의 절반입니다.디스크 브레이크가 있는 앞바퀴나 체인 탈선기가 있는 뒷바퀴와 같은 비대칭 바퀴의 경우 d의 값은 좌우에 따라 다르다.

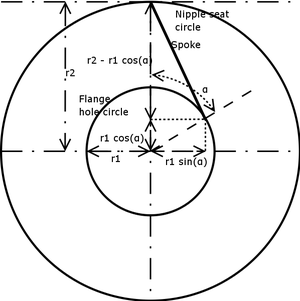
a는 (1) 스포크가 부착된 림의 니플 구멍에 대한 반지름과 (2) 스포크를 고정하는 플랜지 구멍에 대한 반지름 사이의 각도이다.스포크는 레이싱 설계에 따라 반대 방향으로 1, 2, 또는3개의 스포크를 통과합니다.플랜지에서 인접한 구멍의 반지름 사이의 각도는 360°/m(등간격 구멍의 경우)입니다.교차하는 각 스포크에 대해 허브는 림 1을 기준으로 "인접한 플랜지 구멍 사이의 각도"를 기준으로 회전합니다.따라서 "인접한 플랜지 구멍 사이의 각도"에 k를 곱하면 각도 a가 됩니다.예를 들어, 32 스포크 휠은 측면당 16개의 스포크를 가지며 360°를 16으로 나누면 22.5°가 됩니다.22.5°("인접한 플랜지 구멍 사이의 각도")에 교차점 수를 곱하여 각도 a를 구한다. 3개의 교차점이 있는 경우, 32개의 스포크 휠의 각도 a는 67.5°이다.r에₃ 대해서: 플랜지의 스포크 구멍의 크기는 필요한 스포크 길이만큼 중요하지 않습니다.이 항은 홀 크기의 영향을 제거합니다.구멍은 보통 작기 때문에(지름이 2mm를 조금 넘습니다), 효과는 작으며 실제로는 거의 문제가 되지 않습니다.

방사상으로 스포크된 바퀴(교차 제로)의 경우, 공식은 피타고라스 정리로 단순화되며 스포크 길이 l 더하기₃ r은 기울기, r₂ 빼기₁ r은 밑면, d는 상승입니다.

(l+r_{3})^{2}=(r_{2}-r_{1})^{2}+d^{2}

+

(l+r_{3})^{2}=(r_{2}-r_{1})^{2}+d^{2}

3) 2

(l+r_{3})^{2}=(r_{2}-r_{1})^{2}+d^{2}

(

(l+r_{3})^{2}=(r_{2}-r_{1})^{2}+d^{2}

-

(l+r_{3})^{2}=(r_{2}-r_{1})^{2}+d^{2}

)

(l+r_{3})^{2}=(r_{2}-r_{1})^{2}+d^{2}

2 +

(l+r_{3})^{2}=(r_{2}-r_{1})^{2}+d^{2}

(

l

+ r

_

{

3

}^{2} = ( r

_ {2

} -

r

_

{

1} )^{

2}

+ d

2

} ;

또는

길이만큼 해결

{{displaystyle l=sqrt {d^{2}+(r_{2}-r_{1})^{2}}-r_{3}.}

한 개의 스포크가 보이는 교차된 휠의 평면도

파생

스포크 길이 공식은 가상의 직사각형 상자의 공간 대각선 길이를 계산합니다.유두가 맨 위에 오도록 앞에 바퀴를 든다고 상상해 보세요.축을 따라 바퀴를 보세요.위쪽 구멍을 통과하는 스포크는 이제 가상 상자의 대각선이 됩니다.상자의 깊이는 d, 높이는 r-rcos₂₁(α), 폭은 rsin₁(a)입니다.

마찬가지로 코사인 법칙은 바퀴 평면에 투영된 스포크의 길이를 계산하기 위해 사용될 수 있다(그림에 나와 있음). 그 후 피타고라스 정리를 적용할 수 있다.

참고 항목

메모들

^ Neumayer 1800-1200 BC;^[2]^[3] Celeste Paxton 2300-1000 BC)^[4]원형/연석학에 대해서는 브래드쇼 재단, '파치마히 언덕의 선사시대 그림'을 참조하십시오.

레퍼런스

^ 린드너, 스테판, (2020년)"유라시아 스텝의 샤리오트: 기원전 제2천년 초의 마력 수송의 출현에 대한 베이지안 접근법", 고대, 제94권, 제374호, 2020년 4월, 페이지 367: "...신타슈타 지평선에 속하는 12개의 보정된 방사성 탄소 일자는 기원전 2050 - 1760cal 범위(95.4% 신뢰도, 에피마호브 & Krause 2013: 137)이다.이 날짜들은 기원전 2040-1730cal로 거슬러 올라가는 관련 KA-5cemetry에 있는 7개의 AMS 표본 신타슈타 무덤과 잘 연관되어 있다(95.4%))".
^ Neumayer, Erwin. "Chariots in the Chalcolithic Rock Art of Indian" (PDF).
^ harappa.com, 인도의 칼콜리틱 암석예술의 병거
^ Celeste Paxton (2016), 과거로부터의 목소리: 연구자는 40세기에 걸쳐 미스터리를 탐구한다.
^ Neumayer, Erwin (28 March 2013). Prehistoric Rock Art of India. ISBN 978-0198060987.
^ Herlihy, David (2004). Bicycle: the History. Yale University Press. p. 141. ISBN 0-300-10418-9. Retrieved 2009-09-29.
^ "Hansen Wheel and Wagon Shop". 2006. Archived from the original on 2006-08-14. Retrieved 2006-08-22.
^ "PBO Spoke Technology". 2006. Archived from the original on 2011-10-30. Retrieved 2011-10-21.
^ "Basic spokes". Sapim N.V.

외부 링크

온라인 스포크 길이 계산기(독일어)는 위의 공식과 약간 다른 척도를 사용합니다. (독일어)

[5] Neumayer 1800-1200 BC;^[2]^[3] Celeste Paxton 2300-1000 BC)^[4]원형/연석학에 대해서는 브래드쇼 재단, '파치마히 언덕의 선사시대 그림'을 참조하십시오.

[1] 린드너, 스테판, (2020년)"유라시아 스텝의 샤리오트: 기원전 제2천년 초의 마력 수송의 출현에 대한 베이지안 접근법", 고대, 제94권, 제374호, 2020년 4월, 페이지 367: "...신타슈타 지평선에 속하는 12개의 보정된 방사성 탄소 일자는 기원전 2050 - 1760cal 범위(95.4% 신뢰도, 에피마호브 & Krause 2013: 137)이다.이 날짜들은 기원전 2040-1730cal로 거슬러 올라가는 관련 KA-5cemetry에 있는 7개의 AMS 표본 신타슈타 무덤과 잘 연관되어 있다(95.4%))".

[Neumayer_Chariots_slideshow-2] Neumayer, Erwin. "Chariots in the Chalcolithic Rock Art of Indian" (PDF).

[Harappan_Neumayer-3] rappa.com, 인도의 칼콜리틱 암석예술의 병거

[Paxton-4] Celeste Paxton (2016), 과거로부터의 목소리: 연구자는 40세기에 걸쳐 미스터리를 탐구한다.

[6] Neumayer, Erwin (28 March 2013). Prehistoric Rock Art of India. ISBN 978-0198060987.

[Herlihy-7] Herlihy, David (2004). Bicycle: the History. Yale University Press. p. 141. ISBN 0-300-10418-9. Retrieved 2009-09-29.

[Hansen-8] "Hansen Wheel and Wagon Shop". 2006. Archived from the original on 2006-08-14. Retrieved 2006-08-22.

[spinergy-9] "PBO Spoke Technology". 2006. Archived from the original on 2011-10-30. Retrieved 2011-10-21.

[10] "Basic spokes". Sapim N.V.

[1]

[note 1]

[5]

[6]

[7]

[8]

[9]

[2]

[3]

[4]

v t 자전거 부품
틀	핸들바 줄기. 헤드 튜브 헤드셋 포크 시트 포스트 안장 하단 브래킷 포크 엔드 서스펜션
바퀴	타이어 말했다 스포크 니플 밸브 스템 더스트 캡 퀵 릴리즈 꼬치
드라이브 트레인	페달 크랭크 세트 체인 톱니바퀴 세트 탈선 기어/허브 기어 기어 케이스 스프로킷
케이블 접속	시프터 보든 케이블 케이블 가이드 브레이크 페룰
주변기기	바구니 벨 병 케이지 페어링 사이클로컴퓨터 킥스탠드 조명. 러기지 캐리어 머드가드 패니어 새들백 스포크 카드 리플렉터 스커트 가드 트레이닝 휠

Search

말했다

네임스페이스

더

목차

역사

건설