주입 모듈

수학에서, 특히 모듈 이론으로 알려진 추상 대수 영역에서, 주입 모듈은 모든 이성적인 숫자의 Z-모듈 Q와 어떤 바람직한 속성을 공유하는 모듈 Q이다.구체적으로 Q가 일부 다른 모듈의 하위 모듈이라면, 그것은 이미 그 모듈의 직접적인 요약이다. 또한, 모듈 Y의 하위 모듈로 주어진다면, 이 하위 모듈에서 Q까지의 모든 모듈 동형성은 모든 Y에서 Q로 동형성으로 확장될 수 있다.이 개념은 투영 모듈의 개념과 이중적이다.주입 모듈은 (Baer 1940)에 도입되었으며, 교과서(Lam 1999, §3)에서 자세히 논의되고 있다.

주입 모듈은 상당히 많이 연구되었으며, 다양한 추가 개념은 다음과 같이 정의된다.주입식 코제네이터는 모듈의 전체 범주를 충실하게 나타내는 주입식 모듈이다.주입 분해능은 모듈이 주입 치수 측면에서 얼마나 멀리 떨어져 있는지 측정하고 파생 범주의 모듈을 나타낸다.주입식 선체는 최대 필수 연장이며, 최소 주입식 연장인 것으로 밝혀졌다.노메테리아 링 위에서, 모든 주입 모듈은 독특하게 외설적인 모듈들의 직접적인 총합이며, 그 구조는 잘 이해된다.한 링 위에 주입하는 모듈은 다른 링 위에 주입되지 않을 수 있지만, 특별한 경우를 처리하는 링을 변경하는 방법은 잘 이해되어 있다.그 자체로 주입식 모듈인 링은 여러 가지 흥미로운 특성을 가지고 있으며 필드 위에 유한한 그룹의 그룹 링과 같은 링을 포함한다.주입 모듈은 분리할 수 없는 그룹을 포함하며 범주 이론에서 주입 물체의 개념에 의해 일반화된다.

정의

링 R 위의 좌측 모듈 Q는 다음과 같은 동등한 조건 중 하나(따라서 모두)를 만족하는 경우 주입된다.

Q가 일부 다른 좌측 R-모듈 M의 하위 모듈인 경우, M이 Q와 K의 내부 직접 합인 Q와 K의 내부 직접 합인, 즉 Q + K = M과 Q ∩ K = {0}과 같은 M의 다른 하위 모듈 K가 존재한다.
좌측 R-모듈의 0 →Q → M → K → 0의 모든 짧은 정확한 시퀀스가 분할된다.
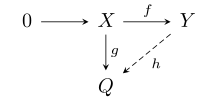
X와 Y가 R-modules, f : X → Y는 주입 모듈 동형성, g : X → Q는 임의 모듈 동형성인 경우, hf = g, 즉 다음과 같은 도표가 통용되는 모듈 동형성 h : Y → Q가 존재한다.

왼쪽 R-모듈 범주에서 아벨 그룹 범주에 이르는 상이한 홈 펑터 홈(-,Q)은 정확하다.

주입식 우측 R-모듈은 완전한 유추로 정의된다.

예

첫 번째 예

0 모듈 {0}은(는) 사소한 경우 주입식입니다.

필드 k가 주어진 모든 k-벡터 공간 Q는 주입식 k-모듈이다.이유: Q가 V의 하위공간이라면 Q의 근거를 찾아 V의 기초로 확장할 수 있다.V의 하위 공간 K에 걸쳐 있는 새로운 확장 기본 벡터는 Q와 K의 내부 직접 합이다.Q의 직접보완 K는 Q에 의해 고유하게 결정되는 것이 아니며, 마찬가지로 위의 정의에서 확장된 맵 h도 일반적으로 고유하지 않다는 점에 유의한다.

이성애자 Q(추가 포함)는 주입 아벨리안 그룹(즉, 주입 Z-모듈)을 형성한다.인자군 Q/Z와 원군군 역시 주입형 Z-모듈이다.n > 1에 대한 인자군 Z/nZ는 Z/nZ-모듈로서 주입되지만 아벨 그룹으로서 주입되지는 않는다.

상쇄적 예

보다 일반적으로, R-모듈 K는 주입식 R-모듈이며, 실제로 R을 포함하는 가장 작은 주입식 R-모듈이다.모든 데데킨드 도메인에서, 지수 모듈 K/ $R_{\mathfrak {p}}/R$ 도 주입성이 있으며, 그것의 외설적인 합계는 0이 아닌 프라임 이상 ${\$ $R_{\$ $mathfrak{p}}$ 에 대한 $R_{\mathfrak {p}}/R$ 지역화 $R_{\mathfrak {p}}/R$ $R_{\mathfrak {p}}/R$ / $R_{\mathfrak {p}}/R$ R ${\$ displaystystyle{p $}/R}$ 이다 ${\mathfrak {p}}$ 제로 이상은 또한 원시적이며 주입 K에 해당한다.이러한 방식으로 주요 이상과 외설적인 주입 모듈 사이에는 1:1의 일치성이 있다.

특히 풍부한 이론은 Eben Matlis, (Lam 1999, §3I)로 인해 상호 작용하는 노메트리안 고리에 사용할 수 있다.모든 주입 모듈은 특이하게 강제 주입식 모듈의 직접적인 합이며, 강제 주입식 모듈은 링의 주요 스펙트럼에 따라 P가 변화하는 시료 R/P의 주입 선체로 고유하게 식별된다.R-모듈로서 R/P의 주입 선체는 표준적으로_P R 모듈이며, R/P의 R-주입_P 선체다.즉, 지역적인 고리를 고려하는 것으로 충분하다.R/P 주입 선체의 내형성 링은 P에서 R의 ${\hat R}_{P}$ 완료 ${\hat {R}}_{P}$ ${\hat {R}}_{P}$ P ${\$ 이다.^[1]

Z-모듈 Z/pZ(Prufer 그룹)의 주입 선체와 k[x]-모듈 k(역대 다항식 링)의 주입 선체 두 가지 예가 있다.후자는 k[x,x⁻¹]/xk[x]로 쉽게 표현된다.이 모듈은 n = 0, 1, 2, …에 대한⁻ⁿ x인 "역방향 단원"으로 구성된다. 스칼라에 의한 곱셈은 예상대로이며, x/1 = 0을 제외하고 x에 의한 곱셈은 정상적으로 동작한다.내형성 링은 그야말로 형식적인 권력 시리즈의 링이다.

아티니아의 예

G가 유한한 집단이고 특성 0을 가진 한 분야라면, 집단표현 이론에서 주어진 하나의 하위표시는 이미 주어진 것의 직접적인 합계라는 것을 보여준다.모듈 언어로 번역하면, 이는 그룹 대수 kG를 통한 모든 모듈이 주입됨을 의미한다.k의 특성이 0이 아닌 경우, 다음과 같은 예가 도움이 될 수 있다.

만약 A가 k보다 유한한 치수를 가진 필드 k에 대한 단이탈적 연관 대수라면, Hom_k(-, k)은 미세하게 생성된 왼쪽 A-모듈과 미세하게 생성된 오른쪽 A-모듈 사이의 이중성이다.따라서 미세하게 생성된 주입 왼쪽 A-모듈은 정밀하게 생성된 오른쪽 A-모듈인 Hom_k(P, k) 형식의 모듈이다.대칭 알헤브라의 경우 이중성은 특히 품행이 단정하고 투영적인 모듈과 주입 모듈이 일치한다.

모든 아르티니아 반지에 대해서는, 교감반지와 마찬가지로, 주요한 이상과 외설적인 주입 모듈 사이에 1-1의 일치성이 있다.이 경우의 대응은 아마도 더 간단할 것이다. 주요한 이상은 독특한 단순한 모듈의 섬멸자, 그리고 그에 상응하는 외설적인 주입 모듈은 그것의 주입식 선체라는 것이다.필드 위의 유한 차원 알헤브라의 경우, 이러한 주입식 선체는 정밀하게 생성된 모듈이다(Lam 1999, §3G, §3J).

컴퓨터 주입 선체

$R$ $R$ 이 $R$ (가) 노메트리안 링이고 ${\mathfrak {p}}$ ${\$ 이 ${\mathfrak {p}}$ (가) 프라임 이상이면 $E=E(R/{\mathfrak {p}})$ = $E=E(R/{\mathfrak {p}})$ / p $){\displaystyle E=E(R/{\mathfak {p})$ 를 주입 선체로 설정하십시오 $E=E(R/{\mathfrak {p}})$ .The injective hull of $R/{\mathfrak {p}}$ over the Artinian ring $R/{\mathfrak {p}}^{k}$ can be computed as the module $(0:_{E}{\mathfrak {p}}^{k})$ . It is a module of the same length as ${\displaystyle R$ 특히 R∙)k[x1,…,)n]∙{\displaystyle R_{\bullet}[x_{1},\ldots{n,x_}]_{\bullet}은 표준 수준별 반지를 {\mathfrak{p}}^{k}}.[2],}및 p)(x1,…,)n){\displaystyle{\mathfrak{p}}=(x_{1},\ldots{n,x_})}, E)나는 Hom(R나는, k){\displaystyle E=\oplu ⊕.s_ ${i}{\text{$ $Hom}}(R_{i},k)}$ 은 $E=\oplus _{i}{\text{Hom}}(R_{i},k)$ 주입식 모듈로, $k$ ${\displaystyle$ k $k$ 을(를) 통해 아티니아 링에 대한 불필요한 주입식 모듈을 계산하는 도구를 제공한다.

자기주장성

An Artin local ring $(R,{\mathfrak {m}},K)$ is injective over itself if and only if $soc(R)$ is a 1-dimensional vector space over $K$ . This implies every local Gorenstein ring which is also Artin is injective over itself since has a 1-dimensional socle.[3]단순한non-example은 반지 R=C[), y]는 최대 이상적인(), y){\displaystyle(x, y)}과 잔류물 분야 C{\displaystyle \mathbb{C}다/(x2,)는 y, y2){\displaystyle R=\mathbb{C}[x, y](x^{2},xy,y^{2})}}. 그것의 받침돌은 C⋅ x⊕ C⋅ y{\displaystyle \mathbb{C}\cdot x\oplus.\m $atsb {C} \cdot$ y $\mathbb {C} \cdot x\oplus \mathbb {C} \cdot y$ 2차원.잔류 필드에는 주입식 선체 ${\text{Hom}}_{\mathbb {C} }(\mathbb {C} \cdot x\oplus \mathbb {C} \cdot y,\mathbb {C} )$ ${\text{Hom}}_{\mathbb {C} }(\mathbb {C} \cdot x\oplus \mathbb {C} \cdot y,\mathbb {C} )$ ${\text{Hom}}_{\mathbb {C} }(\mathbb {C} \cdot x\oplus \mathbb {C} \cdot y,\mathbb {C} )$ ${\text{Hom}}_{\mathbb {C} }(\mathbb {C} \cdot x\oplus \mathbb {C} \cdot y,\mathbb {C} )$ ${\text{Hom}}_{\mathbb {C} }(\mathbb {C} \cdot x\oplus \mathbb {C} \cdot y,\mathbb {C} )$ ${\text{Hom}}_{\mathbb {C} }(\mathbb {C} \cdot x\oplus \mathbb {C} \cdot y,\mathbb {C} )$ ${\text{Hom}}_{\mathbb {C} }(\mathbb {C} \cdot x\oplus \mathbb {C} \cdot y,\mathbb {C} )$ ${\text{Hom}}_{\mathbb {C} }(\mathbb {C} \cdot x\oplus \mathbb {C} \cdot y,\mathbb {C} )$ , ${\text{Hom}}_{\mathbb {C} }(\mathbb {C} \cdot x\oplus \mathbb {C} \cdot y,\mathbb {C} )$ )가 있으며, ${\displaystyle {\text{$ $홈}_{\mathb {C}}(\mathb {C} \cdot$ x $\oplus \mathb$ { $C} \cdot$ y $,\mathb {C})}$ .

모듈 오버 리알헤브라스

특성 0의 $k$ k $k$ 에 ${\mathfrak {g}}$ 대한 Lie 대수 ${\mathfrak {g}}$ ${\$ k} ${\mathfak {g}$ 의 경우 모듈 ${\mathcal {M}}({\mathfrak {g}})$ ${\mathcal {M}}({\mathfrak {g}})$ ) ${\displaystyle {\mathcal {m}({\mathfak {g})$ 범주에는 주입 모듈에 대한 비교적 간단한 설명이 있다 ${\mathcal {M}}({\mathfrak {g}})$ .^[4]범용 봉투 대수를 ${\mathfrak {g}}$ 하여 모든 주입 g {\ $displaystyle {\mathfak$ { $g}$ -module을 ${\mathfrak {g}}$ ${\mathfrak {g}}$ ${\$ -module로 ${\mathfrak {g}}$ 구성할 수 있다.

${\text{홈}_{k}(U({\mathfrak {g}),V)$

일부 $k$ $k$ -vector $k$ $공간$ V{\ $displaystyle$ V $V$ 이 벡터 공간에는 주입 시 ${\mathfrak {g}}$ ${\$ {\ $mathfak {g}$ -module ${\mathfrak {g}}$ 구조가 있음

${\mathfrak {g}\hookrightarrow U({\mathfrak {g})$

${\text{Hom}}_{k}(U({\mathfrak {g}}),V)$ 모든 ${\mathfrak {g}}$ ${\$ -module에는 ${\mathfrak {g}}$ 일부 ${\text{Hom}}_{k}(U({\mathfrak {g}}),V)$ ${\text{Hom}}_{k}(U({\mathfrak {g}}),V)$ ( ${\text{Hom}}_{k}(U({\mathfrak {g}}),V)$ ( ${\text{Hom}}_{k}(U({\mathfrak {g}}),V)$ ) ${\text{Hom}}_{k}(U({\mathfrak {g}}),V)$ , V ${\text{Hom}}_{k}(U({\mathfrak {g}}),V)$ ) ${\displaystyle {\text{\$ data. $홈}_{k}(U({\mathfak$ {g $}),V)}$ 및 ${\text{Hom}}_{k}(U({\mathfrak {g}}),V)$ 모든 주입 ${\mathfrak {g}}$ ${\$ mathfak { $g}$ -module은 ${\mathfrak {g}}$ 일부 ${\text{Hom}}_{k}(U({\mathfrak {g}}),V)$ ${\text{Hom}}_{k}(U({\mathfrak {g}}),V)$ ( U ( ${\text{Hom}}_{k}(U({\mathfrak {g}}),V)$ ) ${\text{Hom}}_{k}(U({\mathfrak {g}}),V)$ , $){\displaystystyle{\text}$ 의 직접 합계임 $홈}_{k}(U({\mathfrak {g}),V)}$ .

이론

노메테리아 링의 구조 정리

교감형 노메트리안링 $R$ {\ $displaystyle$ R $}$ 위에 $R$ 모든 주입 모듈은 외설적인 주입 모듈의 직접적인 합이며, 모든 외설적인 주입 모듈은 원시 ${\mathfrak {p}}$ ${\$ 에 있는 잔류장의 주입 선체. ${\mathfrak {p}}$ 즉, $I\in {\text{Mod}}(R)$ I $I\in {\text{Mod}}(R)$ $I\in {\text{Mod}}(R)$ $I\in {\text{Mod}}(R)$ ${\displaystysty$ $I.$ ${\text{Mod}(R)},$ 이형성이 있다.

$I\cong \bigoplus _{i}E(R/{\mathfrak {p}_{i}})$

p. 다음 p나는{\displaystyle{\mathfrak{E(R/p나는){E(R/{\mathfrak{p}}_{나는})\displaystyle}추가적으로 모듈의injective 껍질 R/p나는{\displaystyle R/{\mathfrak{p}}_{나는}}.[5], 어떤 모듈 M{M\displaystyle} 입으면{\displaystyle 1세}은injective 선체다}}_ ${i}}$ 은 ${\mathfrak {p}}_{i}$ (는) $M$ $M$ 과 $M$ ^[2]와) 연관된 프리타임이다.

서브모듈, 인용문, 제품 및 합계

(무한히 많은) 주입 모듈의 모든 제품은 주입식이다. 반대로, 모듈의 직접 제품이 주입식인 경우, 각 모듈은 주입식이다. (Lam 1999, 페이지 61)미세하게 많은 주입 모듈의 모든 직접 합은 주입이다.일반적으로 하위 모듈, 인자 모듈 또는 무한 직접 주입 모듈은 주입할 필요가 없다.크다면 만약 그 반지를Artinian semisimple(골란&헤드 1991년,p. 152)모든injective 모듈의 모든 submodule, 만일 반지를 유전적인 것마다injective 모듈의 모든 요소 모듈,(람이 1999년 여. 3.22)injective 있으며, 경우에만 만약 그 반지를 Noetheriinjective 모듈의 모든 무한한 직접적인 합injective은injective 있다.,(^[6]Lam 1999, Th 3.46)

바어의 기준

Baer의 원본 논문에서, 그는 모듈 주입 여부를 확인하기 위해, 보통 Baer's Criteria로 알려진 유용한 결과를 증명했다: R의 왼쪽 이상 I에 정의된 어떤 동형상 g : I → Q가 모든 R에 확장될 수 있는 경우에만 왼쪽 R-모듈 Q가 주입된다.

이 기준을 사용하면 Q가 주입 아벨 그룹(즉, Z를 통한 주입 모듈)임을 알 수 있다.더 일반적으로, 아벨리아 집단은 분리될 수 있는 경우에만 주입된다.보다 일반적으로는 고요함: 주 이상영역 위에 있는 모듈은 분할할 수 있는 경우에만 주입된다(모든 장은 주 이상영역이고 모든 벡터공간은 분할할 수 있기 때문에 벡터공간은 이 정리의 예다).일반적 통합영역에 걸쳐서, 우리는 여전히 하나의 함축적 의미를 가지고 있다: 통합영역에 대한 모든 주입 모듈은 분리될 수 있다.

바어의 기준은 (Smith 1981), (Vamos 1983) harv error: no target: CITREFVamos1983 (help) 교감형 노메테리아 링의 경우 프라임 이상만 고려해도 충분하다는 것을 포함하여 여러 가지 면에서 정비되었다(골란 & 헤드 1991, 페이지 119).Baer의 기준 중 투영성 테스트를 할 수 있는 이중성은 일반적으로 거짓이다.예를 들어 Z-모듈 Q는 Baer 기준의 이중성을 만족하지만 투영적이지 않다.

주입식 열병합발전기

아마도 가장 중요한 주입 모듈은 아벨 그룹 Q/Z일 것이다.아벨 그룹 범주에 있는 주입식 열병합발전기로, 주입식이고 다른 모듈도 Q/Z 복사본의 적절한 큰 제품에 포함되어 있다는 것을 의미한다.그래서 특히 모든 아벨 그룹들은 주사파의 한 부분군이다.모든 모듈이 주입식 모듈의 하위 모듈이거나 "좌측 R-모듈의 범주는 충분한 주입물을 가지고 있다"는 점에서 이는 어떤 링에서도 사실이다.이를 증명하기 위해 아벨 그룹 Q/Z의 독특한 특성을 이용하여 왼쪽 R-모듈의 범주에 주입식 열병합발전기를 구성한다.

For a left R-module M, the so-called "character module" M⁺ = Hom_Z(M,Q/Z) is a right R-module that exhibits an interesting duality, not between injective modules and projective modules, but between injective modules and flat modules (Enochs & Jenda 2001, pp. 78–80).어떤 링 R의 경우, 좌측 R-모듈은 해당 문자 모듈이 주입된 경우에만 평탄하다.R이 noetherian으로 남겨진 경우, 왼쪽 R-모듈은 그것의 캐릭터 모듈이 평평한 경우에만 주입된다.

주입 선체

모듈의 주입식 선체는 주어진 것을 포함하는 가장 작은 주입식 모듈이며 (Eckmann & Shopf 1953) harv 오류에 설명되어 있다: 대상 없음: CATEREFeckmannShopf1953 (도움말).

최소 주입 분해능을 정의하기 위해 주입형 선체를 사용할 수 있다(아래 참조).주입 분해능의 각 항이 이전 지도 코커넬의 주입 선체인 경우 주입 분해능의 길이는 최소로 한다.

주입 분해능

또한 모든 모듈 M에는 주입 분해능이 있다: 정확한 폼 시퀀스

0 → M → I⁰ → I¹ → I² → ...

여기서^j I는 주입 모듈이다.주입 분해능은 Ext functor와 같은 파생 functor를 정의하는 데 사용될 수 있다.

유한주입 분해능의 길이는 첫 번째 지수 n으로, I가ⁿ n보다 크면ⁱ I = 0이다.모듈 M이 유한주입 분해능을 인정하는 경우, M의 모든 유한주입 분해능 중 최소 길이를 그것의 주입 치수라고 하며, ID(M)로 표시한다. 만일 M이 유한주입 분해능을 인정하지 않는다면, 관례상 주입 치수는 무한하다고 한다.(Lam 1999, §5C) 예를 들어 id(M) = 0과 같은 모듈 M을 고려한다. 이 상황에서 시퀀스 0 → M → I → 0의⁰ 정확성은 중앙의 화살표가 이형성임을 나타내며, 따라서 M 자체는 주입성임을 나타낸다.^[7]

동등하게, M의 주입 치수는 최소 정수(그렇지 않으면 ∞) n이며, Ext^N
_A(–,M) = 모든 N > n에 대해 0이다.

외설물

주입 모듈의 모든 주입식 하위절은 직접 합산으로, 따라서 불필요한 주입식 모듈을 이해하는 것이 중요하다. (Lam 1999, §3F)

모든 외설적인 주입 모듈에는 국소 내형성 링이 있다.0이 아닌 두 개의 하위조항마다 0이 아닌 교차점이 있으면 모듈은 균일한 모듈이라고 불린다.주입 모듈 M의 경우 다음과 같다.

M은 외설적이다.
M은 0이 아니며 모든 0이 아닌 하위 모듈의 주입 선체임
M은 균일하다.
M은 균일한 모듈의 주입 선체임
M은 균일한 주기 모듈의 주입 선체다.
M은 국소 내형성 링을 가지고 있다.

노메트리안 링 위에서, 모든 주입 모듈은 외설적인 주입 모듈의 직접적인 합이다.상호 작용하는 노메테리아 링을 통해, 이것은 (Matlis 1958년)에 설명된 모든 주입 모듈을 특히 잘 이해할 수 있게 해준다.외설적인 주입 모듈은 R링의 가장 이상적인 p를 위한 R/p 모듈의 주입 선체다.더욱이 R/p의 주입 선체 M은 이상 p의ⁿ 섬멸자가 주는 모듈 M에_n 의한 여과가 증가하며, M_n+1/M은_n R/p 대 Hom_R/p(partⁿ/pⁿ⁺¹, k(p)의 quitient field k(p)에 대한 유한차원 벡터 공간으로서 이소모픽이다.

반지 교환

특히 다항식 링과 같은 서브링이나 지수 링보다 모듈을 고려할 수 있는 능력이 중요하다.일반적으로 이것은 어렵지만, 많은 결과가 알려져 있다. (Lam 1999, 페이지 62)

S와 R을 링으로 하고, P는 좌-R 모듈처럼 평평한 좌-R, 우-S 바이모듈이 된다.모든 주입 우측 S-모듈 M에 대해 모듈 동형성 Hom_S(P, M ) 집합은 주입 우측 R-모듈이다.좌우의 속성을 서로 바꾸어 놓고도 물론 같은 말이 성립된다.

예를 들어, 만약 R이 S의 서브링으로 S가 평평한 R-모듈이라면, 모든 주입 S-모듈은 주입식 R-모듈이다.특히, R이 통합 영역이고 S가 그것의 분수 영역이라면, S 위의 모든 벡터 공간은 주입식 R-모듈이다.마찬가지로 모든 주입식 R[x]-모듈은 주입식 R-모듈이다.

반대 방향에서 링 동형상 $f:S\to R$ : $f:S\to R$ → R ${\displaystyle f:$ $S\to R}$ 은(는) 왼쪽과 오른쪽의 곱셈으로 R을 왼쪽-R, 오른쪽-S 바이모듈로 만든다 $f:S\to R$ .스스로 자유로워지는 R 또한 좌 R-모듈처럼 평평하다.P = R에 대해 위의 문구를 전문으로 하면, M이 주입 우측 S-모듈일 때 코인듀싱 모듈 f $f_{*}M=\mathrm {Hom} _{S}(R,M)$ M $f_{*}M=\mathrm {Hom} _{S}(R,M)$ = H $f_{*}M=\mathrm {Hom} _{S}(R,M)$ m $f_{*}M=\mathrm {Hom} _{S}(R,M)$ ( $f_{*}M=\mathrm {Hom} _{S}(R,M)$ $f_{*}M=\mathrm {Hom} _{S}(R,M)$ $f_{*}M=\mathrm {Hom} _{S}(R,M)$ ) $f_{*}M=\mathrm {Hom} _{S}(R,M)$ 이 $f_{*}M=\mathrm {Hom} _{S}(R,M)$ 주입 우측 R-모듈이라고 되어 있다.따라서 f에 대한 코인전도는 주입 S-모듈로부터 주입 R-모듈을 생성한다.

지수 링 R/I의 경우 링의 변화도 매우 분명하다.R-모듈은 I에 의해 전멸되었을 때 정확하게 R/I-모듈이다.ann_I(M) = {m in M : im = 0 in I}의 모든 I에 대한 서브모듈은 왼쪽 R-모듈 M의 왼쪽 서브모듈이며, R/I모듈인 M의 가장 큰 서브모듈이다.M이 주입식 좌측 R-모듈이라면 앤_I(M)은 주입식 좌측 R/I-모듈이다.이것을 R=Z, I=nZ, M=Q/Z에 적용하면 Z/nZ가 스스로 모듈로서 주입된다는 익숙한 사실을 얻게 된다.주입형 R-모듈을 주입형 R/I-모듈로 변환하기는 쉽지만, 이 프로세스는 주입형 R-resolution을 주입형 R/I-resolution으로 변환하지 않으며, 결과 복합체의 호몰로지(homology)는 상대동문대수학 연구의 초기 및 기초 분야 중 하나이다.

교과서(Rotman 1979, 페이지 103)는 국산화에서 주입물을 보존한다는 잘못된 증거를 가지고 있지만, (Dade 1981년)에서 백범례가 주어졌다.

자기주사 링

단일성을 가진 모든 링은 자유 모듈이므로 스스로 모듈로서 투영되지만 링이 스스로 모듈로서 주입되는 경우는 드물다(Lam 1999, §3B).링이 우측 모듈로서 그 자체로 주입되는 경우, 우측 자기주사 링이라고 한다.모든 프로베니우스 대수학은 자기주장을 받지만, 필드가 아닌 일체영역은 자기주장을 하지 않는다.데데킨드 도메인의 모든 적절한 지분은 자기주장을 초래한다.

오른쪽 노메테리아, 오른쪽 자기주사반지는 준 프로베니우스 반지라고 불리며, 양면 아르티니아어 및 양면 주입이다(Lam 1999, Th. 15.1).준 Frobenius 링의 중요한 모듈 이론적 특성은 투사 모듈이 정확히 주입 모듈이라는 것이다.

일반화 및 전문화

주입물체

또한 모듈 범주보다 범주의 주입 물체에 대해서도 언급한다. 예를 들어, functor 범주 또는 일부 링 공간(X_X,O)에 대한 O-module의_X 범주에서 말이다.다음과 같은 일반적 정의를 사용한다: C 범주의 객체 Q는 단형주의 f : X → Y 그리고 어떤 형태주의 g : X → Q에 대하여 hf = g가 있는 형태주의 h : Y → Q가 존재한다면 주입된다.

분리할 수

아벨 그룹 범주에서 주입 물체의 개념은 분할 그룹이라는 용어에 따른 주입 모듈과는 다소 독립적으로 연구되었다.여기서 Z-모듈 M은 0이 아닌 정수 n마다 n⋅M = M인 경우에만 주입된다.여기서 평면 모듈, 순수 하위 모듈 및 주입 모듈 사이의 관계는 단순히 정수에 의한 모듈 요소의 특정 구분성 특성을 언급하기 때문에 더욱 명확하다.

순수주사

상대적 동질대수학에서 동질성의 확장 속성은 전체보다는 특정 하위 항목에 대해서만 요구될 수 있다.예를 들어, 순수 주입 모듈은 순수 하위 모듈의 동형성이 전체 모듈로 확장될 수 있는 모듈이다.

참조

메모들

^ "Lemma 47.7.5 (08Z6)—The Stacks project". stacks.math.columbia.edu. Retrieved 2020-02-25.
^ ^a ^b Eisenbud. Introduction to Commutative Algebra. pp. 624, 625.
^ "Injective Modules" (PDF). p. 10.
^ Vogan, David. "Lie Algebra Cohomology" (PDF).
^ "Structure of injective modules over Noetherian rings".
^ Bass-Papp 정리(Pap 1959) 및 (Chase 1960) 참조
^ 주입 모듈에 이형화된 모듈은 당연히 주입된다.

교과서

Anderson, Frank Wylie; Fuller, Kent R (1992), Rings and Categories of Modules, Berlin, New York: Springer-Verlag, ISBN 978-0-387-97845-1, retrieved 30 July 2016
Enochs, Edgar E.; Jenda, Overtoun M. G. (2000), Relative homological algebra, de Gruyter Expositions in Mathematics, vol. 30, Berlin: Walter de Gruyter & Co., doi:10.1515/9783110803662, ISBN 978-3-11-016633-0, MR 1753146
Golan, Jonathan S.; Head, Tom (1991), Modules and the structure of rings, Monographs and Textbooks in Pure and Applied Mathematics, vol. 147, Marcel Dekker, ISBN 978-0-8247-8555-0, MR 1201818
Lam, Tsit-Yuen (1999), Lectures on modules and rings, Graduate Texts in Mathematics No. 189, Berlin, New York: Springer-Verlag, doi:10.1007/978-1-4612-0525-8, ISBN 978-0-387-98428-5, MR 1653294
Rotman, Joseph J. (1979), An introduction to homological algebra, Pure and Applied Mathematics, vol. 85, Boston, MA: Academic Press, ISBN 978-0-12-599250-3, MR 0538169

일차 출처

Baer, Reinhold (1940), "Abelian groups that are direct summands of every containing abelian group", Bulletin of the American Mathematical Society, 46 (10): 800–807, doi:10.1090/S0002-9904-1940-07306-9, MR 0002886, Zbl 0024.14902
Chase, Stephen U. (1960), "Direct products of modules", Transactions of the American Mathematical Society, American Mathematical Society, Vol. 97, No. 3, 97 (3): 457–473, doi:10.2307/1993382, JSTOR 1993382, MR 0120260
Dade, Everett C. (1981), "Localization of injective modules", Journal of Algebra, 69 (2): 416–425, doi:10.1016/0021-8693(81)90213-1, MR 0617087
Eckmann, B.; Schopf, A. (1953), "Über injektive Moduln", Archiv der Mathematik, 4 (2): 75–78, doi:10.1007/BF01899665, MR 0055978
Lambek, Joachim (1963), "On Utumi's ring of quotients", Canadian Journal of Mathematics, 15: 363–370, doi:10.4153/CJM-1963-041-4, ISSN 0008-414X, MR 0147509
Matlis, Eben (1958), "Injective modules over Noetherian rings", Pacific Journal of Mathematics, 8: 511–528, doi:10.2140/pjm.1958.8.511, ISSN 0030-8730, MR 0099360
Osofsky, B. L. (1964), "On ring properties of injective hulls", Canadian Mathematical Bulletin, 7: 405–413, doi:10.4153/CMB-1964-039-3, ISSN 0008-4395, MR 0166227
Papp, Zoltán (1959), "On algebraically closed modules", Publicationes Mathematicae Debrecen, 6: 311–327, ISSN 0033-3883, MR 0121390
Smith, P. F. (1981), "Injective modules and prime ideals", Communications in Algebra, 9 (9): 989–999, doi:10.1080/00927878108822627, MR 0614468
Utumi, Yuzo (1956), "On quotient rings", Osaka Journal of Mathematics, 8: 1–18, ISSN 0030-6126, MR 0078966
Vámos, P. (1983), "Ideals and modules testing injectivity", Communications in Algebra, 11 (22): 2495–2505, doi:10.1080/00927878308822975, MR 0733337

[1] "Lemma 47.7.5 (08Z6)—The Stacks project". stacks.math.columbia.edu. Retrieved 2020-02-25.

[:0-2] Eisenbud. Introduction to Commutative Algebra. pp. 624, 625.

[3] "Injective Modules" (PDF). p. 10.

[4] Vogan, David. "Lie Algebra Cohomology" (PDF).

[5] "Structure of injective modules over Noetherian rings".

[6] Bass-Papp 정리(Pap 1959) 및 (Chase 1960) 참조

[7] 주입 모듈에 이형화된 모듈은 당연히 주입된다.

[1]

[4]

[2]

[6]

[7]

Search