다면체 클래스 번호 및 속성 플라톤 고형 (5 , 볼록, 정규) 아르키메데스 고형물 (13 , 볼록, 균일) 케플러-푸인소트 다면체 (4 , 일반, 비일반) 균일다면체 (75 , 균일) 프리즘아토이드 :프리즘 , 반격 등 (4개 의 무한 균일 클래스) 폴리헤드라 틸팅 (11 일반 , 평면 내) 준정규다면체 (8 ) 존슨 고형물 (92 , 볼록, 비수동) 피라미드 와 비피라미드 (무한 ) 스텔링스 스텔링스 다면 화합물 (5정규 ) 델타헤드라속 (델타헤드 라, 등변 삼각형 면) 스너브 다면체 (12 유니폼 , 미러 이미지가 아님) 조노헤드론 (조노헤드 라, 면은 180° have) 이중 다면체 자가이중다면체 (무한 ) 카탈루냐 고체 (13 , 아르키메데스 이중)
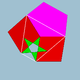
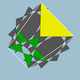
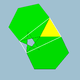
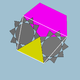
획일적인 다면체 사이에는 많은 관계가 있다.[1] [2] [3] 어떤 것은 정규 또는 준정규 다면체의 정점을 잘라내어 얻는다. 다른 것들은 다른 다면체와 같은 정점과 가장자리를 공유한다. 아래의 그룹들은 이러한 관계의 일부를 보여준다.
다면체의 꼭지점 모양 각 꼭지점에 인접한 면들을 나열하여 얻은 정점 수치 를 조사하여 관계를 명확히 할 수 있다(일률적인 다면체의 경우 모든 정점이 동일하다는 것, 즉 정점-변환 이라는 것을 기억하라). 예를 들어, 큐브에는 정점 그림 4.4.4, 즉 세 개의 인접한 정사각형 면들이 있다. 가능한 얼굴들은
3 - 정삼각형 4 제곱 5 - 일반 펜타곤 6 - 일반 육각형 8 - 정규 8각형 10 - 일반 데카곤 5/2 - 펜타그램 8/3 - 옥타그램 10/3 - 디카그램 어떤 면은 여기에 다음과 같이 쓰여진 역방향으로 나타날 것이다.
다른 것들은 우리가 쓴 기원을 통과한다.
Wythoff 기호는 다면체와 구형 삼각형 을 연관시킨다.Wythoff 기호는 p q r, p q r, p q r라고 쓰여 있다. 여기서 구형 삼각형은 π/p, q, q/r의 각도를 가지며, 막대는 삼각형을 기준으로 정점의 위치를 나타낸다.
존슨(2000년)은 다음과 같이 균일한 다면체를 분류했다.
정규(일반적인 다각형 정점 그림): pq , Wythoff 기호 q 페이지 2 준정규(직사각형 또는 직사각형): p.q.p.q 2 p q 또는 p.q.p.p.q.q, Wythoff 기호 3 p q. Versi-general(정사각 정점 수치), p.q*—p.q*, Wythoff 기호 q p. 잘린 정규(등각 삼각 정점 그림): p.p.q, Wythoff 기호 q 2p Versi-Quasi-정점(입체 정점 수치), p.q.p.r Wythoff 기호 q r p 준준정규(사다리꼴 꼭지점 수치): p*.q.p* q.r* 또는 p.q* q.q* p q.r. 잘린 준정규(scalene 삼각정점 수치), p.q.r Wythoff 기호 p q r 스너브 준정규형(펜타곤, 육각형 또는 팔각정점), Wythoff 기호 p q r 프리즘(잘린 호소헤드라), 반격 및 교차 반격(스누브 디헤드라) 각 그림의 형식은 동일한 기본 패턴을 따른다.
다면체의 이미지 다면체의 이름 대체 이름(괄호 포함) 와이토프 기호 번호 부여 시스템: Wenninger가 폴리헤드 사용 등 에서는 C - 번호 부여. '유니폼 폴리헤드라' 유형별 정점 V, 에지 E, 면 F 및 면 수. 오일러 특성 χ = V - E + F 정점 수치는 왼쪽에 있고, 점 그룹은 3차원으로 표시 된다. #남은 7개 의 점군d , 사면 T, 팔면 Oh 또는 이면 Ih .
잘린 양식 일반 다면체 및 잘린 형태 A열에는 모든 정규 다면체, B열에는 잘린 형태가 나열된다. 일반 다면체에는 모두 정점 그림r p: p.p.p 등과 Wythoff 기호 p q r가 있다. 잘린 형태는 정점 그림 Q.q.r(여기서 q=2p 및 r)과 Wythoff p q r을 가지고 있다.
꼭지점 모양 무리를 짓다 A: 정규: p.p.p.p. B: 잘린 정규: p.p.r. 3.3.3 3.6.6
Td 사면체 3 2 3 W1, U01, K06, C15 V 4,E 6,F 4=4{3} χ =2
잘린 사면체 2 3 3 W6, U02, K07, C16 V 12,E 18,F 8=4{3}+4{6} χ =2
3.3.3.3 4.6.6
Oh 팔면체 4 2 3, 34 W2, U05, K10, C17 V 6,E 12,F 8=8{3} χ =2
잘린 팔면체 2 4 3 W7, U08, K13, C20 V 24,E 36,F 14=6{4}+8{6} χ =2
4.4.4 3.8.8
Oh 육면체 (큐브) 3 2 4 W3, U06, K11, C18 V 8,E 12,F 6=6{4} χ =2
잘린 육면체 2 3 4 W8, U09, K14, C21 V 24,E 36,F 14=8{3}+6{8} χ =2
3.3.3.3.3 5.6.6
Ih 이코사헤드론 5 2 3 W4, U22, K27, C25 V 12,E 30,F 20=20{3} χ =2
잘린 이코사면체 2 5 3 W9, U25, K30, C27 E 60,V 90,F 32=12{5}+20{6} χ =2
5.5.5 3.10.10
Ih 도데카헤드론 3 2 5 W5, U23, K28, C26 V 20,E 30,F 12=12{5} χ =2
잘린 도두면체 2 3 5 W10, U26, K31, C29 V 60,E 90,F 32=20{3}+12{10} χ =2
5.5.5.5.5 5/2.10.10
Ih 대두면체 5 /2 2 5W21, U35, K40, C44 V 12,E 30,F 12=12{5} χ =-6
잘린 대두면체 25 /2 5 W75, U37, K42, C47 V 60,E 90,F 24=12{5 /2 }+12{10} χ =-6
3.3.3.3.3 5/2.6.6.
Ih 대이코사면체 (제16회 이코사면체) 5 /2 2 3W41, U53, K58, C69 V 12,E 30,F 20=20{3} χ =2
크게 잘린 이코사면체 25 /2 3 W95, U55, K60, C71 V 60,E 90,F 32=12{5 /2 }+20{6} χ =2
5/2.5/2.5/2.5/2.5/2
Ih 소절개도면체 5 25 /2 W20, U34, K39, C43 V 12,E 30,F 12=12{5 /2 } χ =-6
5/2.5/2.5/2
Ih 그레이트 스틸 도데카헤드론 3 25 /2 W22, U52, K57, C68 V 20,E 30,F 12=12{5 /2 } χ =2
게다가 세 가지 준경사형도 있다. 이것들은 또한 잘린-정규적인 다면체로 분류된다.
꼭지점 숫자 O조h 1조h 1조h 3.8/3.8/3 5.10/3.10/3 3.10/3.10/3
잘린 육면체 (정량 처리된 육면체) (stellatrunculated cube) 2 3 4 /3 W92, U19, K24, C66 V 24,E 36,F 14=8{3}+6{8 /3 } χ =2
잘린 작은 도데면체 (Quasitrunced small stelled dodecheadron) (소형 스테라트론 도데카헤드론) 2 5 5 /3 W97, U58, K63 V 60,E 90,F 24=12{5}+12{10 /3 } χ =-6
대절개 자른 도데카헤드론 (Quasitrunced great stelled dodecheadron) (대단백질도면체) 2 3 5 /3 W104, U66, K71, C83 V 60,E 90,F 32=20{3}+12{10 /3 } χ =2
준정규 다면체의 잘린 형태 A열은 일부 준정규 다면체를 나열하고, B열은 정상적인 잘린 형태를 나열하고, C열은 준잘린 형태를 표시하며, D열은 다른 잘린 방법을 보여준다. 이러한 잘린 형태는 모두 꼭지점 그림 p.q.r과 Wythoff 기호를 가지고 있다.
꼭지점 모양 무리를 짓다 A: 준정규어: p.q.p.q. B: 잘린 준정규어: p.q.r C: 잘린 준정규어: p.q.r D: 잘린 준정규어: p.q.r 3.4.3.4 4.6.8 4.6.8/3 8.6.8/3
Oh 큐폭타헤드론 2 3 4 W11, U07, K12, C19 V 12,E 24,F 14=8{3}+6{4} χ =2
잘린 큐옥타헤드론 (위대한 롬비큐보옥타헤드론) 2 3 4 W15, U11, K16, C23 V 48,E 72,F 26=12{4}+8{6}+6{8} χ =2
잘린 큐옥타헤드론 (Quasitrunced cuboctaheadron) 2 34 /3 W93, U20, K25, C67 V 48,E 72,F 26=12{4}+8{6}+6{8 /3 } χ =2
큐비트런드 큐빅토크헤드론 (Cuboctatrun cuboctatrun cuboctaheadron) 3 44 /3 W79, U16, K21, C52 V 48,E 72,F 20=8{6}+6{8}+6{8 /3 } χ =-4
3.5.3.5 4.6.10 4.6.10/3 10.6.10/3
Ih 이코시다데카헤드론 2 3 5 W12, U24, K29, C28 V 30,E 60,F 32=20{3}+12{5} χ =2
잘린 이코시다데카헤드론 (위대한 롬비코시도데카헤드론) 2 3 5 W16, U28, K33, C31 V 120,E 180,F 62=30{4}+20{6}+12{10} χ =2
크게 잘린 이코시다데카헤드론 (위대한 퀘이시트론경화 이코시다데카헤드론) 2 35 /3 W108, U68, K73, C87 V 120,E 180,F 62=30{4}+20{6}+12{10 /3 } χ =2
이코시트룬말살도데코헤드론 (이코시도데카트룬갈린이코시도데카헤드론) 3 55 /3 W84, U45, K50, C57 V 120,E 180,F 44=20{6}+12{10}+12{10 /3 } χ =-16
5/2.5.5/2.5 4.10.10/3
Ih
도데카데카헤드론 2 5 5 /2 W73, U36, K41, C45 V 30,E 60, F 24=12{5}+12{5 /2 } χ =-6
잘린 도데코데카헤드론 (Quasitrunculated dodecheadron) 2 55 /3 W98, U59, K64, C75 V 120,E 180,F 54=30{4}+12{10}+12{10 /3 } χ =-6
3.5/2.3.5/2
Ih 대이코시다데카헤드론 2 3 5 /2 W94, U54, K59, C70 V 30,E 60, F 32=20{3}+12{5 /2 } χ =2
폴리헤드라 공유 에지 및 정점 정규 이것들은 모두 다른 곳에 언급되어 있지만, 이 표는 약간의 관계를 보여준다. 그것들은 모두 버시-정기인 사트라헤미헥사헤드론과는 별도로 규칙적이다.
꼭지점 모양 V E 무리를 짓다 정칙의 정시/정시 정시 정시 3.3.3.3 3.4*.-3.4*
6 12 Oh 팔면체 4 2 3 W2, U05, K10, C17 F 8=8{3} χ =2
테트라헤미헥사헤드론 3 /2 3 2W67, U04, K09, C36 F 7=4{3}+3{4} χ =1
3.3.3.3.3 5.5.5.5.5
12 30 Ih 이코사헤드론 5 2 3 W4, U22, K27 F 20=20{3} χ =2
대두면체 5 /2 2 5W21, U35, K40, C44 F 12=12{5} χ =-6
5/2.5/2.5/2.5/2.5/2 3.3.3.3.3
12 30 Ih 소절개도면체 5 25 /2 W20, U34, K39, C43 F 12=12{5 /2 } χ =-6
대이코사면체 (제16회 이코사면체) 5 /2 2 3W41, U53, K58, C69 F 20=20{3} χ =2
준정규직 및 versi정규직 직사각형 정점수 또는 교차된 직사각형 첫 번째 열은 준정규형 두 번째 열이고 세 번째 열은 일부 저자에 의해 versi-정규형 이라고 불리는 원점을 통과하는 얼굴이 있는 헤미헤드라이다 .
꼭지점 모양 V E 무리를 짓다 준정기: p.q.p.q. versi-general: p.s* esxp.s* versi-general: Q.s*ylq.s* 3.4.3.4 3.6*.-3.6* 4.6*.-4.6*
12 24 Oh 큐폭타헤드론 2 3 4 W11, U07, K12, C19 F 14=8{3}+6{4} χ =2
옥타헤미오크타헤드론 3 /2 3 3W68, U03, K08, C37 F 12=8{3}+4{6} χ =0
큐보헤미오크타헤드론 4 /3 4 3W78, U15, K20, C51 F 10=6{4}+4{6} χ =-2
3.5.3.5 3.10*.-3.10* 5.10*.-5.10*
30 60 Ih 이코시다데카헤드론 2 3 5 W12, U24, K29, C28 F 32=20{3}+12{5} χ =2
소이코시헤미도데코헤드론 3 /2 3 5W89, U49, K54, C63 F 26=20{3}+6{10} χ =-4
소도데카헤미도데코헤드론 5 /4 5 5W91, U51, K56, 65 F 18=12{5}+6{10} χ =-12
3.5/2.3.5/2 3.10*.-3.10* 5/2.10*.-5/2.10*
30 60 아이히 대이코시다데카헤드론 2 5 /2 3 W94, U54, K59, C70 F 32=20{3}+12{5 /2 } χ =2
대이코시헤미도데코헤드론 3 3 5 /3 W106, U71, K76, C85 F 26=20{3}+6{10 /3 } χ =-4
대 도데카헤미도데코헤드론 5 /3 5 /2 5 /3 W107, U70, K75, C86 F 18=12{5 /2 }+6{10 /3 } χ =-12
5.5/2.5.5/2 5.6*.-5.6* 5/2.6*.-5/2.6*
30 60 아이히 도데카데카헤드론 2 5 /2 5 W73, U36, K41, C45 F 24=12{5}+12{5 /2 } χ =-6
도데카헤미코사헤드론 5 /4 5 3W102, U65, K70, C81 F 22=12{5}+10{6} χ =-8
작은 도데카헤미코사헤드론 5 /3 5 /2 3W100, U62, K67, C78 F 22=12{5 /2 }+10{6} χ =-8
직교정규격 및 versi정규격 직사각형(ditrigonal, 즉 di(2) -tri(3)-ogonal) 정점 수치는 직사각형의 3배 아날로그다. 이것들은 모든 가장자리가 이등형이기 때문에 모두 준정형 이다. 5-Cube의 화합물은 동일한 세트의 가장자리와 꼭지점을 공유한다. 십자형 형태는 방향성 이 맞지 않는 꼭지점을 가지기 때문에 "- 표기법은 사용되지 않았고 "*" 면은 원점을 통과하기보다는 가까운 곳을 지나간다.
꼭지점 모양 V E 무리를 짓다 직각의 교차 직경의 교차 직경의 5/2.3.5/2.3.5/2.3 5/2.5*.5/2.5*.5/2. 5* 3.5*.3.5*.3.5*
20 60 아이히 소형 이코시다데카헤드론 3 5 /2 3 W70, U30, K35, C39 F 32=20{3}+12{5 /2 } χ =-8
직교 도데코데카헤드론 3 5 /3 5 W80, U41, K46, C53 F 24=12{5}+12{5 /2 } χ =-16
대직류 이코시다데카헤드론 3 /2 3 5W87, U47, K52, C61 F 32=20{3}+12{5} χ =-8
versi-the-general과 준-si-general. 그룹 III: 사다리꼴 또는 교차 사다리꼴 꼭지점 수치 첫 번째 열에는 큐보타헤드론과 이코시도데카헤드론의 꼭지점 수치에 두 개의 정사각형을 삽입하여 만든 볼록형 다면체(Volfx rhombic polyedra가 있다.
꼭지점 모양 V E 무리를 짓다 사다리꼴: p.q.r.q. 크로스-트라페조이드: p.s*-r.s* 교차 사다리꼴: Q.s* .-q.s* 3.4.4.4 3.8*.-4.8* 4.8*.-4.8*
24 48 Oh 소형 롬비큐옥타헤드론 (롬비큐브옥타헤드론) 3 4 2 W13, U10, K15, C22 F 26=8{3}+(6+12){4} χ =2
소형입방옥타헤드론 3 /2 4 4W69, U13, K18, C38 F 20=8{3}+6{4}+6{8} χ =-4
작은 rhombihexahedron 2 3 /2 4 W86, U18, K23, C60 F 18=12{4}+6{8} χ =-6
3.8/3.4.8/3 3.4*.-4.4* 8/3.4*.-8/3.4*
24 48 오호 대입방옥타헤드론 3 4 4 /3 W77, U14, K19, C50 F 20=8{3}+6{4}+6{8 /3 } χ =-4
비콘벡스 대롬비쿠옥타헤드론 (Quasirhombicuboctaheadron) 3 /2 4 2W85, U17, K22, C59 F 26=8{3}+(6+12){4} χ =2
대록비헥사헤드론 2 4 /3 3 /2 W103, U21, K26, C82 F 18=12{4}+6{8 /3 } χ =-6
3.4.5.4 3.10*.-5.10* 4.10*.-4.10*
60 120 Ih 소형 롬비코시도데카헤드론 (롬비코시다데코헤드론) 3 5 2 W14, U27, K32, C30 F 62=20{3}+30{4}+12{5} χ =2
소도데키도데코데카헤드론 3 /2 5 5W72, U33, K38, C42 F 44=20{3}+12{5}+12{10} χ =-16
소형 롬비도데카헤드론 25 /2 5 W74, U39, K44, C46 F 42=30{4}+12{10} χ =-18
5/2.4.5.4 5/2.6*.-5.6* 4.6*.-4.6*
60 120 아이히 롬비도데코데카헤드론 5 /2 5 2W76, U38, K43, C48 F 54=30{4}+12{5}+12{5 /2 } χ =-6
이코시다데코데카헤드론 5 /3 5 3W83, U44, K49, C56 F 44=12{5}+12{5 /2 }+20{6} χ =-16
롬비코사헤드론 2 35 /2 W96, U56, K61, C72 F 50=30{4}+20{6} χ =-10
3.10/3.5/2.10/3 3.4*.-5/2.4 * 10/3.4*.-10/3. 4*
60 120 아이히 대식도데코데카헤드론 5 /2 3 5 /3 W99, U61, K66, C77 F 44=20{3}+12{/}+5 2 12{/}+12{/10 3 }} χ =-16
비콘벡스 대롬비코시도데카헤드론 (Quasirhombicosidodecahedron) 5 /3 3 2W105, U67, K72, C84 F 62=20{3}+30{4}+12{5 /2 } χ =2
대롬비도데카헤드론 2 3 /2 5 /3 W109, U73, K78, C89 F 42=30{4}+12{10 /3 } χ =-18
3.6.5/2.6 3.10*.-5/2.10* 6.10*.-6.10*
60 120 아이히 작은이코시도데카헤드론 5 /2 3 3W71, U31, K36, C40 F 52=20{3}+12{5 /2 }+20{6} χ =-8
소두구체도치데카헤드론 5 /3 3 5W82, U43, K48, C55 F 44=20{3}+12{5 /2 }+12{10} χ =-16
소십면체 3 3 /2 5 W90, U50, K55, C64 F 32=20{6}+12{10} χ =-28
3.10/3.5.10/3 3.6*.-5.6* 10/3.6*.-10/3. 6*
60 120 아이히 대디트리곤 도디코시도데카헤드론 3 5 5 /3 W81, U42, K47, C54 F 44=20{3}+12{5}+12{10 /3 } χ =-16
대이코시토다이데코헤드론 3 /2 5 3W88, U48, K53, C62 F 52=20{3}+12{5}+20{6} χ =-8
대반면체 3 5 /3 5 /2 W101, U63, K68, C79 F 32=20{6}+12{10 /3 } χ =-28
참조 ^ Coxeter, H. S. M. ; Longuet-Higgins, M. S. ; Miller, J. C. P. (1954), "Uniform polyhedra", Philosophical Transactions of the Royal Society of London , 246 : 401–450 (6 plates), doi :10.1098/rsta.1954.0003 , MR 0062446 ^ Sopov, S. P. (1970), "A proof of the completeness on the list of elementary homogeneous polyhedra", Ukrainskiĭ Geometricheskiĭ Sbornik (8): 139–156, MR 0326550 ^ Skilling, J. (1975), "The complete set of uniform polyhedra", Philosophical Transactions of the Royal Society of London , 278 : 111–135, doi :10.1098/rsta.1975.0022 , MR 0365333