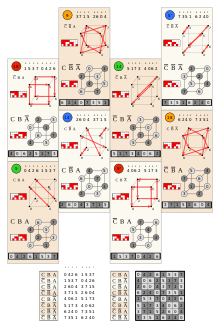
초옥타헤드랄군

C2 그룹은 이 원과 같이 8번 순서를 가지고 있다.

C3(Oh) 그룹은 이러한 구형 삼각형 반사 도메인에서 볼 수 있듯이 순서 48을 가지고 있다.

수학에서 하이퍼옥타헤드 그룹은 하이퍼큐브나 교차폴리토프의 대칭의 집단으로 실현될 수 있는 중요한 유형의 집단이다.1930년에 알프레드 영에 의해 이름이 지어졌다.이러한 유형의 그룹은 하이퍼큐브의 치수인 매개변수 n으로 식별된다.

Coxeter 그룹으로서 타입 B_n = C이고_n, Weyl 그룹으로서 그것은 동정체 그룹과 홀수 치수의 직교 그룹과 연관된다.화환제품으로 $S{\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle S_{}}$ n ${\$이며, $여기$서 ${\displaystyle {Sn}_{}}${\$displaystyle S_{n}}$는 도 n의 대칭 그룹이다.순열 그룹으로서, 그룹은 모든 i에 대해 π(i) = -n(-i) = -n(-i) = -n(-i) = -n(-i) = -n + 1, ..., -1, 1, 2, ..., n } 집합 중 하나 또는 { -n, -n + 1, ..., n } 집합의 서명된 대칭 그룹이다.행렬 그룹으로서, 모든 항목이 정수인 n×n 직교 행렬의 그룹으로 설명할 수 있다.마찬가지로, 이 값은 0 ${\displaystyle 0},$1 ${\displaystyle$ 1}$또는$-${\displaystyle 1}$ ${\displaystyle$ -1}$항목$만 $있는{\displaystyle \mathrm{}}$ n×n 행렬 집합이며$,$ 이 행렬은 변환할 수 없으며 각 행 또는 열에 0이 아닌 항목이 정확히 하나 있다.초옥타헤드 그룹의 대표이론은 (1930년)에 의해 (커버 1971년, 페이지 2)에 의해 설명되었다.

3차원에서 초옥타헤드 그룹은 O×S로₂ 알려져 있으며, 여기서 OsS는₄ 8각형 그룹이고, S는₂ 순서 2의 대칭 그룹(여기서 순환 그룹)이다.이 대칭군을 가진 3차원의 기하학적 도형은 정팔면체 또는 정삼각형의 이름을 따서 팔면대칭이 있다고 한다.4차원에서는 정규 16세포, 즉 4정맥의 이름을 따서 육각대칭이라고 부른다.2차원에서 초옥타헤드 그룹 구조는 정사각형, 즉 2정형의 대칭을 묘사하는 순서 8의 추상적 이면체군이다.

치수별

하이퍼옥타헤드 그룹은 B_n, 괄호 표기법 또는 Coxeter 그룹 그래프로 명명할 수 있다.

n	대칭 무리를 짓다	Bn	콕시터 표기법		주문	거울	구조	관련 일반 폴리토페스
2	D4(*4•)	B2	[4]		222! = 8	4	${\displaystyle Dih_{4}}$ ${\displaystyle \cong S_{2}\wr S_{2}}$	정사각형, 팔각형
3	Oh(*432)	B3	[4,3]		233! = 48	3+6	${\displaystyle S_{4}\time S_{2}$ ${\displaystyle \cong S_{2}\wr S_{3}}$	정육면체, 팔면체
4	±/[16OxO]2 [1] (O/V;O/V)*[2]	B4	[4,3,3]		244! = 384	4+12	${\displaystyle S_{2}\wr S_{4}}$	테세락트, 16셀, 24셀
5		B5	[4,3,3,3]		255! = 3840	5+20	${\displaystyle S_{2}\wr S_{5}}$	5각형, 5각형
6		B6	[4,34]		266! = 46080	6+30	${\displaystyle S_{2}\wr S_{6}}$	6시 30분, 6시 30분
...n		Bn	[4,3n-2]	...	2nn! = (2n)!!	n2	${\displaystyle S_{2}\wr S_{n}}$	하이퍼큐브, 정형외과

부분군

Coxeter 그룹 D와_n demihpercube의 대칭에 해당하는 주목할 만한 지수 2 부분군이 있다.화환제품으로 보면, 초옥타헤드랄군에서 순서 2의 순환군까지 2개의 자연지도가 있는데, ${\displaystyle \mathrm{1개}}$의 지도는 "모든 원소들의 표식"에서 나온 지도$(\{{\displaystyle }$± 1${\displaystyle \}}$ ${\displaystyle \{\pm 1\})$와 $$1개의 지도는 순열의 패리티에서 나온 지도다.이 둘을 곱하면 세 번째 맵 ${\displaystyle C_{}}$ $n{\displaystyle {}_{}}$→${\displaystyle }${${\displaystyle }$± ${\displaystyle 1}$ ${\displaystyle \}}$ ${\displaystyle C_{n}\\{\pm$ 1$\backslash \}\}$이 생성된다.첫 번째 맵의 커널은 Coxeter $그룹{\displaystyle {}_{}}$ ${\displaystyle D_{}}$ .${\displaystyle D_{n}$이다.$}}$ 서명한 순열, 행렬로 생각되는 이$$ 제3지도가 단순히 결정요인인인 데 반해, 앞의 두 가지는 "비영점 순열의 다중화"와 "근거 (서명되지 않은) 순열의 패리티"에 해당하는데, 이는 일반적으로 행렬에는 의미가 없지만 화환제품과의 우연의 일치로 인해 해당된다.

이 세 가지 맵의 낟알은 모두 아래의₁ H: 아벨리아화에서 논한 바와 같이 초옥타헤드 그룹의 3가지 지수 2 하위그룹이며, 이들의 교차점은 지수 4(클라인 4-그룹)의 파생된 하위그룹으로 데미퍼큐브의 회전 대칭에 해당한다.

다른 방향에서 중심은 스칼라 행렬의 부분군이며, {±1}; 기하학적으로, 이를 통한 인지도는 투영직교 그룹에 전달되는 것에 해당한다.

치수 2에서 이 그룹들은 순서가 8인 이음 그룹 Dih이고₄ (순서가 2인 순환 그룹에 의한 4 그룹의) 확장인 초옥타헤드 그룹을 완전히 설명한다.일반적으로 하위 수량(원래 부분군, 모드의 중심)에 전달되는 것은 투영적 디미하이퍼큐브의 대칭 그룹이다.

D_n 치수 기준 초옥타헤드 부분군:

n	대칭 무리를 짓다	Dn	콕시터 표기법		주문	거울	관련 폴리토페스
2	D2(*2•)	D2	[2] = [ ]×[ ]		4	2	직사각형
3	Td(*332)	D3	[3,3]		24	6	사면체
4	±/[13TxT]2 [3] (T/V;T/V)−*[4]	D4	[31,1,1]		192	12	16 셀
5		D5	[32,1,1]		1920	20	5데미큐브
6		D6	[33,1,1]		23040	30	6데미큐브
...n		Dn	[3n-3,1,1]	...	2n-1n!	n(n-1)	데미하이퍼큐브

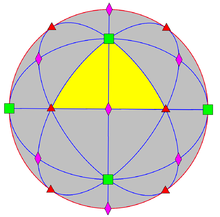
치랄 초극극 대칭은 초극극 대칭의 직접 부분군, 지수 2이다.

n	대칭 무리를 짓다	콕시터 표기법		주문
2	C4 (4•)	[4]+		4
3	O (432)	[4,3]+		24
4	1/6[O×O].2 [5] (O/V;O/V) [6]	[4,3,3]+		192
5		[4,3,3,3]+		1920
6		[4,3,3,3,3]+		23040
...n		[4,(3n-2)+]	...	2n-1n!

또 다른 주목할 만한 지수 2 부분군을 치수별로 초-피리토헤드 대칭이라고 할 수 있다.^[7]이 그룹들은 n-차원 직교 거울을 가지고 있다.

n	대칭 무리를 짓다	콕시터 표기법		주문	거울	관련 폴리토페스
2	D2(*2•)	[4,1+]=[2]		4	2	직사각형
3	Th(3*2)	[4,3+]		24	3	팔면체를 잘라내다.
4	±1/3[T×T].2 [8] (T/V;T/V)*[9]	[4,(3,3)+]		192	4	24셀을 훔치다
5		[4,(3,3,3)+]		1920	5
6		[4,(3,3,3,3)+]		23040	6
...n		[4,(3n-2)+]	...	2n-1n!	n

호몰로지

초옥타헤드 그룹의 집단 동질성은 대칭 집단과 유사하며 안정적 호모토피 이론의 의미에서 안정화를 보인다.

H₁: 아벨리아화

아벨리아화에 동의하는 첫 번째 호몰로지 그룹은 클라인 4개 그룹에서 안정화되며, 다음과 같이 주어진다.

${\displaystyle H_{1}(C_{n},\mathbf {Z})={\begin{case}0&n=0\\\\mathbf {Z} /2&n=1\\\\mathbf {Z} /2\time \mathbf {Z} /2n\geq\case}.}$

This is easily seen directly: the ${\displaystyle -1}$ elements are order 2 (which is non-empty for ${\displaystyle n\geq 1}$), and all conjugate, as are the transpositions in ${\displaystyle S_{n}}$ (which is non-empty for ${\displaystyle n\geq 2}$), and these are two separate classes.이러한 요소들은 그룹을 생성하기 때문에 두 개의 그룹으로 구분되지 않는 유일한 ${\displaystyle \mathrm{아벨리아제이션}}$은 2개 그룹으로 구분되며, 이들 클래스 중 하나는 두 개의 별도 클래스인 만큼$$ -${\displaystyle 1}$ ${\displaystyle \in }${${\displaystyle }$± 1 ${\displaystyle \},}$ ${\displaystyle -1\in \{\pm 1\}}$에 독립적으로 전송될 수 있다.지도는 명시적으로 "모든 원소의 표시의 산물" $(\{{\displaystyle }$ ±${\displaystyle 1\}}$ ${\displaystyle$\{\$pm$ 1$\}$의 n 사본에 있음)$$과 순열의 표시로 주어진다.이 둘을 곱하면 세 번째 비교 지도(이 두 클래스를 모두${\displaystyle }$- 1 ${\displaystyle$ -1$}$에 보내는 행렬의 결정 $요인$)$$가 생성되며, 이 맵과 함께 4-그룹을 형성한다.

H₂: 슈르 승수

고전적으로 슈르 승수로 알려진 두 번째 호몰로지 집단은 (이하라 & 요코누마 1965)에서 계산되었다.

다음 구성 요소:

${\displaystyle H_{2}(C_{n},\mathbf {Z} )={\begin{cases}0&n=0,1\\\mathbf {Z} /2&n=2\\(\mathbf {Z} /2)^{2}&n=3\\(\mathbf {Z} /2)^{3}&n\geq 4\end{cases}}.}$

메모들

참조