레니아

레니아로부터의 자율 패턴의 샘플.

레니아에서 글라이더의 움직임을 보여주는 애니메이션.

Lenia는 Bert Wang-Chak ^[1]^[2]^[3]Chan이 개발한 셀룰러 오토마타 패밀리입니다.이것은 Conway의 Game of Life의 연속적인 일반화를 의도하고 있습니다.레니아에서 생성된 복잡한 자율 패턴("생명체" 또는 "우주선")은 연속적인 고해상도 영역의 결과로 "기하학, 메타아메리카, 퍼지, 복원력, 적응성 및 규칙 일반"^[1]으로 다른 셀 오토마타에 나타나는 패턴과 다르게 묘사된다.

레니아는 교토에서 열린^[4] 유전 및 진화 계산 콘퍼런스에서 2018년 버추얼 크리쳐스 콘테스트를 수상했으며,^[5] 도쿄에서 열린 ALIFE 2018에서 ALIFE 아트 어워드를 수상했습니다.

규칙.

반복적인 갱신

L $(\$ $})$ 을 ${\mathcal {L}}$ $S^{\mathcal {L}}$ 의 상태 S $(\displaystyle$ S $^{\mathcal$ { $L$ 를 포함하는 격자 또는 그리드라고 합니다. ${\mathcal {L}}$ 셀룰러 오토마타와 마찬가지로 Lenia는 반복적으로 갱신됩니다.각 출력 상태는 이전 상태의 순수한 함수입니다.

{\displaystyle\Phi(A^{0})=A^{\Delta t},\Phi(A^{\Delta t})=A^{2\Delta t},\ldots,\Phi(A^{t})=A^{t+\Delta t},\ldots }

$A^{0}$ 서 A 0 $(\$ })은 $\Phi :S^{\mathcal {L}}\rightarrow S^{\mathcal {L}}$ 초기 상태이고 $\Phi :S^{\mathcal {L}}\rightarrow S^{\mathcal {L}}$ : $\Phi :S^{\mathcal {L}}\rightarrow S^{\mathcal {L}}$ $\Phi :S^{\mathcal {L}}\rightarrow S^{\mathcal {L}}$ $→$ $\Phi :S^{\mathcal {L}}\rightarrow S^{\mathcal {L}}$ L {\ $displaystyle \Phi$ : $S^{\mathcal {L}}\rightarrow$ S $^{\mathcal {L}})$ 은 모든 $xdisplay {\mathbstyle}$ 의 로컬 규칙 적용을 나타내는 글로벌 규칙입니다. $\Phi ^{N}(A^{t})=A^{t+N\Delta t}$ = $A^{t+N\Delta$ t $}}.$

시뮬레이션이 각 시간 단계에서 $\Delta t$ t(\ $displaystyle \Delta$ t $)$ 씩 $\Delta t$ 진행되면 시간 $T={\frac {1}{\Delta t}}$ T $T={\frac {1}{\Delta t}}$ $T={\frac {1}{\Delta t}}$ $T={\frac {1}{\Delta t}}$ t $(\$ T $=sqfrac {1}{\Delta$ t $T={\frac {1}{\Delta t}}$ 가 됩니다.

상태 세트

$S=\{0,1,\ldots ,P-1,P\}$ $S=\{0,1,\ldots ,P-1,P\}$ { $S=\{0,1,\ldots ,P-1,P\}$ , $S=\{0,1,\ldots ,P-1,P\}$ , $S=\{0,1,\ldots ,P-1,P\}$ , $S=\{0,1,\ldots ,P-1,P\}$ - $S=\{0,1,\ldots ,P-1,P\}$ , $P }$ , P $=$ \ { $0$ , $1$ , \ $ldots$ , $S=\{0,1,\ldots ,P-1,P\}$ P - 1, P \ $S=\{0,1,\ldots ,P-1,P\}$ } , $P\in \mathbb {Z}$ P $z$ Z $P\in \mathbb {Z}$ （ \ $displaystyle P$ \ $in$ \ $mathbb$ { Z $P\in \mathbb {Z}$ } ）。이것은 오토매틱의 상태 세트이며 각 사이트에서 찾을 수 있는 가능한 상태를 나타냅니다.P $(\displaystyle$ P $)$ 가 $클수록$ 시뮬레이션에서 높은 상태 분해능에 해당합니다 $P$ .많은 셀룰러 오토마타는 가능한 한 낮은 상태 해상도( $P=1$ : P $P=1$ { $displaystyle$ P $=1$ 를 사용합니다. Lenia는 훨씬 높은 해상도를 허용합니다.각 사이트의 실제 값은 [ $]({displaystyle [0,P])$ 가 $[0,P]$ 아니라 $\Delta p={\frac {1}{P}}$ $\Delta p={\frac {1}{P}}$ $\Delta p={\frac {1}{P}}$ P(\ $displaystyle \Delta$ p $=squalfrac {1}{P$ 의 정수 배수이므로 $A^{t}(\mathbf {x} )\in [0,1]$ t $A^{t}(\mathbf {x} )\in [0,1]$ ) $A^{t}(\mathbf {x} )\in [0,1]$ 0 $A^{t}(\mathbf {x} )\in [0,1]$ $A^{t}(\mathbf {x} )\in [0,1]$ $>$ $display$ a $^{t}$ in { $mathb$ }(\ $f})$ 가 $A^{t}(\mathbf {x} )\in [0,1]$ . $cal {L$ $P=4$ 를 들어, $P=4$ $=$ 4 {\ $displaystyle P=$ $\mathbf {A} ^{t}(\mathbf {x} )\in [0,0.25,0.75,1]$ $\mathbf {A} ^{t}(\mathbf {x} )\in [0,0.25,0.75,1]$ t ( $\mathbf {A} ^{t}(\mathbf {x} )\in [0,0.25,0.75,1]$ $\mathbf {A} ^{t}(\mathbf {x} )\in [0,0.25,0.75,1]$ , [ $,$ 0.25 $\mathbf {A} ^{t}(\mathbf {x} )\in [0,0.25,0.75,1]$ $\mathbf {A} ^{t}(\mathbf {x} )\in [0,0.25,0.75,1]$ . $\mathbf {A} ^{t}(\mathbf {x} )\in [0,0.25,0.75,1]$ , 1 $](\displaystyle$ \ $mathbf {A}$ ^ { $t} \in [ 0$ , $0$ . $25$ , 0 . 75 $1$

인근 지역

'Game of Life'에 사용된 것과 같은 9평방미터의 무어 지역입니다.

레니아가 사용하던 '공' 동네.

수학적으로 Game of Life와 $같은$ 주변은 $\mathbb {R} ^{2}$ 의 $\mathbb {R} ^{2}$ 벡터 세트를 사용하여 나타낼 수 있습니다. 예를 들어, Game of Life에서 사용되는 고전적인 Moore $\mathbb {R} ^{2}$ 근방의 ${\mathcal {N}}=\{-1,0,1\}^{2}$ N ${\mathcal {N}}=\{-1,0,1\}^{2}$ { ${\mathcal {N}}=\{-1,0,1\}^{2}$ - ${\mathcal {N}}=\{-1,0,1\}^{2}$ , 0 , $}$ 2 { \ $display$ style { $mathcal$ $\mathbb {R} ^{2}$ { N} $\mathbb {R} ^{2}$ $=$ { 0 , 1 } = { 0 , 1 } ${$ 1 } $^{$ $1$ 、 1 } $\mathbb {R} ^{2}$ 、 1 }모든 사이트에서 d.

Lenia의 경우 인근은 ${\mathcal {N}}=\{\mathbf {x} \in {\mathcal {L}}:\lVert \mathbf {x} \rVert _{2}\leq R\}$ N ${\mathcal {N}}=\{\mathbf {x} \in {\mathcal {L}}:\lVert \mathbf {x} \rVert _{2}\leq R\}$ { ${\mathcal {N}}=\{\mathbf {x} \in {\mathcal {L}}:\lVert \mathbf {x} \rVert _{2}\leq R\}$ L : ${\mathcal {N}}=\{\mathbf {x} \in {\mathcal {L}}:\lVert \mathbf {x} \rVert _{2}\leq R\}$ ${\mathcal {N}}=\{\mathbf {x} \in {\mathcal {L}}:\lVert \mathbf {x} \rVert _{2}\leq R\}$ ${\mathcal {N}}=\{\mathbf {x} \in {\mathcal {L}}:\lVert \mathbf {x} \rVert _{2}\leq R\}$ $}$ R $}$ { $displaystyle$ {N} = \ { \ $mathbf$ { x } \ $in \ mathcal$ { L ${\mathcal {N}}=\{\mathbf {x} \in {\mathcal {L}}:\lVert \mathbf {x} \rVert _{2}\leq R\}$ } : \ $lvert$ \ $Mathbrt$ { $L }$ 의 $R$ 볼입니다.

인접 벡터는 요소의 절대 위치가 아니라 특정 사이트에 대한 상대 위치(델타) 세트입니다.

로컬 규칙

레니아에는 별개의 변종과 연속적인 변종이 있습니다. $(\$ 를 $\mathbf {x}$ ${\mathcal {L}}$ $\mathbb {R} ^{2}$ $(\$ L}) 내의 ${\mathcal {N}}$ $R2(\$ $displaystyle \$ $mathbbb$ { $R} ^{$ 2}) ${\mathcal {N}}$ 로 $하고,$ N $\mathbb {R} ^{2}$ $(\$ $displaystyle {$ $N$ $\mathbf {x}$ 을 ${\mathcal {N}}$ $사이트$ 집합으로 합니다 $.$ 2단계 상승:

컨볼루션 $\mathbf {K} :{\mathcal {N}}\rightarrow S$ K : $\mathbf {K} :{\mathcal {N}}\rightarrow S$ {\ $displaystyle \mathbf$ {K} : {\mathcal { $N}}\rightarrow$ S $}$ 를 $\mathbf {K} :{\mathcal {N}}\rightarrow S$ 사용하여 전위 $\mathbf {U} ^{t}(\mathbf {x} )=\mathbf {K} *\mathbf {A} ^{t}(\mathbf {x} )$ U $\mathbf {U} ^{t}(\mathbf {x} )=\mathbf {K} *\mathbf {A} ^{t}(\mathbf {x} )$ t ( $\mathbf {U} ^{t}(\mathbf {x} )=\mathbf {K} *\mathbf {A} ^{t}(\mathbf {x} )$ ) $\mathbf {U} ^{t}(\mathbf {x} )=\mathbf {K} *\mathbf {A} ^{t}(\mathbf {x} )$ A $\mathbf {U} ^{t}(\mathbf {x} )=\mathbf {K} *\mathbf {A} ^{t}(\mathbf {x} )$ t $\mathbf {U} ^{t}(\mathbf {x} )=\mathbf {K} *\mathbf {A} ^{t}(\mathbf {x} )$ ( $\mathbf {U} ^{t}(\mathbf {x} )=\mathbf {K} *\mathbf {A} ^{t}(\mathbf {x} )$ ) \ $displaystyle \mathbf { U$ } $^{t}(\mathbf$ {x} \mathbf} \mathbf} \mathbf} $→$ { $BF}$ \mathb}를 계산합니다.
성장 $G:[0,1]\rightarrow [-1,1]$ G : $G:[0,1]\rightarrow [-1,1]$ [ $G:[0,1]\rightarrow [-1,1]$ , $G:[0,1]\rightarrow [-1,1]$ ] $G:[0,1]\rightarrow [-1,1]$ [ - $G:[0,1]\rightarrow [-1,1]$ 1 , $]$ { { $displaystyle$ G : [ $0$ , $1$ ] \ $rightarrow$ [ - $1 ]$ }를 $G:[0,1]\rightarrow [-1,1]$ 사용하여 최종 성장 $\mathbf {G} ^{t}(\mathbf {x} )=G(\mathbf {U} ^{t}(\mathbf {x} ))$ $\mathbf {G} ^{t}(\mathbf {x} )=G(\mathbf {U} ^{t}(\mathbf {x} ))$ t ( $\mathbf {G} ^{t}(\mathbf {x} )=G(\mathbf {U} ^{t}(\mathbf {x} ))$ ) $\mathbf {G} ^{t}(\mathbf {x} )=G(\mathbf {U} ^{t}(\mathbf {x} ))$ G ( $\mathbf {G} ^{t}(\mathbf {x} )=G(\mathbf {U} ^{t}(\mathbf {x} ))$ t ( $\mathbf {G} ^{t}(\mathbf {x} )=G(\mathbf {U} ^{t}(\mathbf {x} ))$ ) \ $displaystyle$ \ $mathbf { G$ } ^ { t ^ { $t$ } = G ( $mathb$ x ) （ mathb x ） = G ) （ mathb x ) （ G $）$

$\mathbf {G} ^{t}$ t $\mathbf {G} ^{t}$ { $G} ^{$ t}}가 $\mathbf {G} ^{t}$ 계산되면 선택한 시간 분해능 $\Delta t$ t {\ $displaystyle \Delta$ t $}$ 에 $\Delta t$ 따라 크기가 조정되어 원래 상태 값에 추가됩니다.

\displaystyle \mathbf {A} ^{t+\Delta t}(\mathbf {x}) = text{t}(\mathbf {A} ^{t} +\mathbf {G}) ^{t}(\mathbf {x}),\;0,\1)}

여기서 클립 함수는 clip

\operatorname {clip} (v,a,b):=\min(\max(u,a),b)

\operatorname {clip} (v,a,b):=\min(\max(u,a),b)

v ,

\operatorname {clip} (v,a,b):=\min(\max(u,a),b)

,

\operatorname {clip} (v,a,b):=\min(\max(u,a),b)

) :

\operatorname {clip} (v,a,b):=\min(\max(u,a),b)

\operatorname {clip} (v,a,b):=\min(\max(u,a),b)

( max

\operatorname {clip} (v,a,b):=\min(\max(u,a),b)

(

\operatorname {clip} (v,a,b):=\min(\max(u,a),b)

a

\operatorname {clip} (v,a,b):=\min(\max(u,a),b)

)

\operatorname {clip} (v,a,b):=\min(\max(u,a),b)

,

\operatorname {clip} (v,a,b):=\min(\max(u,a),b)

) { displaystyle \

operatorname { v

, a ,

b

(

v

, a , b )로 정의됩니다.

=\min(\max(u,a,

b)}.

로컬 규칙은 개별 Lenia 및 연속 Lenia에 대해 다음과 같이 정의됩니다.

{nmbfault}:{n}:{n}:{n}F}:{n}:{n}:{n}F}:{n2}}:{n){nmFA:엔드{ 사례s}}\\mathbf {G} ^{t}(\mathbf {x})&=G(\mathbf {U} ^{t}(\mathbf {x})\\mathbf {A} ^{t+\Delta t}(\mathbf {x})&text{t}(\mathbf})

커널 생성

Lenia의 커널 셸, 커널 스켈레톤 및 성장 매핑.

컨볼루션 $\mathbf {K}$ K $(\$ 를 생성하는 방법은 여러 가지가 있습니다.마지막 커널은 커널 $K_{C}$ $K_{C}$ C $(\$ K_ ${C})$ 와 $K_{C}$ 커널 $K_{S}$ $K_{S}$ S $(\$ 의 구성입니다.

커널 $K_{C}$ $K_{C}$ C $K_{C}$ {\ $style$ K_ ${C$ 의 경우 Chan은 방사형으로 정의된 여러 함수를 제공합니다.커널 셸 함수는 단일이며 K $K(0)=K(1)=1$ ( $K(0)=K(1)=1$ ) $K(0)=K(1)=1$ ( $K(0)=K(1)=1$ ) $K(0)=K(1)=1$ $K(0)=K(1)=1$ { $display style$ K ( 0 ) $= K$ (1) $=$ 1 $($ $K_{C}\left({\frac {1}{2}}\right)=1$ 으로 $K_{C}\left({\frac {1}{2}}\right)=1$ C $K_{C}\left({\frac {1}{2}}\right)=1$ ( $K_{C}\left({\frac {1}{2}}\right)=1$ ) $K_{C}\left({\frac {1}{2}}\right)=1$ { $display style$ K_ ${C}\left ({\frac {2}}\right$ ) $= 1$ )의 $K_{C}\left({\frac {1}{2}}\right)=1$ $K(0)=K(1)=1$ 조건도 따릅니다.커널 함수의 예는 다음과 같습니다.

(\displaystyle K_{C}(r)=sysp begin{case}\exp \left(\alpha - {\frac {4r }{-r}}}}}\right), & {\text {refential}, \alpha = 4\\alpha = {\f}, {\f}\f}, {\f}, {\f}, {\f}, {\f}, {\f}, {\f}, {\f},\f}, {\f}, {\f},}}\end {case}}

$\mathbf {1} _{A}(r)$ 서 $\mathbf {1} _{A}(r)$ ( $\mathbf {1} _{A}(r)$ $){style \mathbf {$ 1 $} _{A}(r)}$ 는 $\mathbf {1} _{A}(r)$ 인디케이터 함수입니다.

커널 셸이 정의되면 커널 $K_{S}$ $K_{S}$ S $(\$ 를 $K_S$ 사용하여 셸을 일련의 동심원 링으로 변환하여 커널의 실제 값을 계산합니다.각 고리의 높이는 커널 피크 $\beta =(\beta _{1},\beta _{2},\ldots ,\beta _{B})\in [0,1]^{B}$ β $\beta =(\beta _{1},\beta _{2},\ldots ,\beta _{B})\in [0,1]^{B}$ ( $\beta =(\beta _{1},\beta _{2},\ldots ,\beta _{B})\in [0,1]^{B}$ $\beta =(\beta _{1},\beta _{2},\ldots ,\beta _{B})\in [0,1]^{B}$ , $\beta =(\beta _{1},\beta _{2},\ldots ,\beta _{B})\in [0,1]^{B}$ 2, $\beta =(\beta _{1},\beta _{2},\ldots ,\beta _{B})\in [0,1]^{B}$ $\beta =(\beta _{1},\beta _{2},\ldots ,\beta _{B})\in [0,1]^{B}$ B ) $\beta =(\beta _{1},\beta _{2},\ldots ,\beta _{B})\in [0,1]^{B}$ [ 0 $\beta =(\beta _{1},\beta _{2},\ldots ,\beta _{B})\in [0,1]^{B}$ , $\beta =(\beta _{1},\beta _{2},\ldots ,\beta _{B})\in [0,1]^{B}$ ] $\beta =(\beta _{1},\beta _{2},\ldots ,\beta _{B})\in [0,1]^{B}$ B { \ $displaystyle$ \ = ( \ $displaystyle _$ {2} , \ $ldots$ , \ $in [ 0$ , 1 $\beta =(\beta _{1},\beta _{2},\ldots ,\beta _{B})\in [0,1]^{B}$ 에 의해 제어된다. ${B$ $B$ 서 B $(\style$ B $)$ 는 $B$ 파라미터 벡터의 순위입니다.다음으로 커널 $K_{S}$ $(\$ K_ ${S})$ 는 $K_S$ 다음과 같이 정의됩니다.

(RFilesa)=(RRFlor \}K_{c}:{c}:{c}:{c}:{c}:

최종 커널은 {kbF {n}(가)입니다.

\mathbf {n} (\mathbf {n} ) = flac {K_{S}(\lVert \mathbf {n} \rVert _{2}} {K_{S} }

K $(\$ 는 $\mathbf {K}$ $1$ 이 1 $(\displaystyle$ 1)이고 $1$ K $displaystyle \mathbf {K} *\mathbf {A}\$ 이 $\mathbf {K}$ 정규화한다(질량 보존). $|K_{S}|=\textstyle \sum _{\mathcal {N}}\displaystyle K_{S}\,\Delta x^{2}$ $|K_{S}|=\textstyle \sum _{\mathcal {N}}\displaystyle K_{S}\,\Delta x^{2}$ $|K_{S}|=\textstyle \sum _{\mathcal {N}}\displaystyle K_{S}\,\Delta x^{2}$ $|K_{S}|=\textstyle \sum _{\mathcal {N}}\displaystyle K_{S}\,\Delta x^{2}$ $|K_{S}|=\textstyle \sum _{\mathcal {N}}\displaystyle K_{S}\,\Delta x^{2}$ K $|K_{S}|=\textstyle \sum _{\mathcal {N}}\displaystyle K_{S}\,\Delta x^{2}$ $|K_{S}|=\textstyle \sum _{\mathcal {N}}\displaystyle K_{S}\,\Delta x^{2}$ $|K_{S}|=\textstyle \sum _{\mathcal {N}}\displaystyle K_{S}\,\Delta x^{2}$ \ $displaystyle$ K _ { $S$ } = \ $textstyle$ \ $sum$ _ { \ $mathcal$ { $N$ $\int _{N}K_{S}\,dx^{2}$ } \ $displaystyle$ K _ { $S$ } , \ $Delta$ x ${2$ $\int _{N}K_{S}\,dx^{2}$ $\int _{N}K_{S}\,dx^{2}$ S $\int _{N}K_{S}\,dx^{2}$ 2 \ style \ $int _$ { N }

성장 맵핑

성장 매핑 G : [ 0 $G:[0,1]\rightarrow [-1,1]$ 1 $G:[0,1]\rightarrow [-1,1]$ [ - $G:[0,1]\rightarrow [-1,1]$ , $]{$ $displaystyle$ G : $G:[0,1]\rightarrow [-1,1]$ [ $0$ , $1$ ]\ $rightarrow$ [ - $1$ , 1 $G:[0,1]\rightarrow [-1,1]$ $\mu ,\sigma \in \mathbb {R}$ 는 액티베이션 함수와 $\mu ,\sigma \in \mathbb {R}$ 하며 파라미터 $\mu ,\sigma \in \mathbb {R}$ μ , $displaystyle$ , \ $in$ \ $mathbb$ 의 예를 받아들이는 함수일 수 있습니다 $.$

={Num}:{Num}:{Num}:{n2}}:{n2}}:{n2}}:{n2}}:{n2}}:{n2}}:{n2}}점 &{t.t{etc.}}\end{case}}

$u$ 서u\ $displaystyle$ u는 $u$ U $\mathbf {U} ^{t}$ \ $displaystyle\mathbf {U}$ ^{ $t$ 에서 추출한 잠재적 값입니다.

게임 오브 라이프

Game of $R=T=P=1$ 는 $R=T=P=1$ = $R=T=P=1$ P $R=T=P=1$ 1 {\ $displaystyle R$ 1}인 이산형 레니아의 특수한 경우로 간주할 수 있습니다. 이 경우, 커널은 직사각형이며, 함수는

{\displaystyle K_{C}(r)=\mathbf {1}_{\left[{\frac {1}{4}},\right]}(r)+{\frac {1}{1}_{\left[0,\frac {4}}\right})

성장규칙도 직사각형으로 μ

\mu =0.35,\sigma =0.07

0.

\mu =0.35,\sigma =0.07

\mu =0.35,\sigma =0.07

\mu =0.35,\sigma =0.07

0.

(\displaystyle \mu = 0.35,\display = 0.07

입니다.

패턴

레니아에 있는 매우 다양한 "종"들 중 일부입니다.

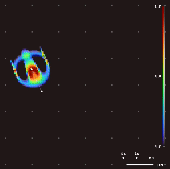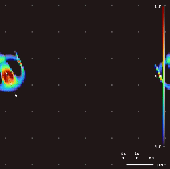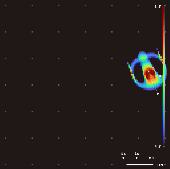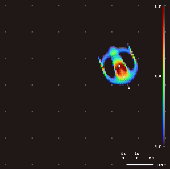
컨볼루션 커널, 성장 맵핑 및 초기 조건을 바꿈으로써 레니아에서 400종 이상의 "생명체"가 발견되어 "자기 조직화, 자기 복구, 쌍방향 및 방사형 대칭, 기관 동역학, 그리고 때로는 혼돈스러운 성질"^[6]을 보여 왔다.Chan은 이러한 ^[1]패턴에 대한 분류법을 만들었습니다.

「」를 참조해 주세요.

외부 링크

레퍼런스

^ ^a ^b ^c Hong Kong; Chan, Bert Wang-Chak (2019-10-15). "Lenia: Biology of Artificial Life". Complex Systems. 28 (3): 251–286. doi:10.25088/ComplexSystems.28.3.251.
^ "Lenia". chakazul.github.io. Retrieved 2021-10-12.
^ Roberts, Siobhan (2020-12-28). "The Lasting Lessons of John Conway's Game of Life". The New York Times. ISSN 0362-4331. Retrieved 2021-10-13.
^ "The virtual creatures competition". virtualcreatures.github.io. Retrieved 2021-10-12.
^ "ALife Art Award 2018". ALIFE Art Award 2018. Retrieved 2021-10-12.
^ "Lenia". chakazul.github.io. Retrieved 2021-10-13.
^ Gilpin, William (2019-09-04). "Cellular automata as convolutional neural networks". Physical Review E. 100 (3): 032402. doi:10.1103/PhysRevE.100.032402. ISSN 2470-0045.
^ Mordvintsev, Alexander; Randazzo, Ettore; Niklasson, Eyvind; Levin, Michael (2020-02-11). "Growing Neural Cellular Automata". Distill. 5 (2): e23. doi:10.23915/distill.00023. ISSN 2476-0757.
^ Gilpin, William (2019-09-04). "Cellular automata as convolutional neural networks". Physical Review E. 100 (3): 032402. doi:10.1103/PhysRevE.100.032402. ISSN 2470-0045.

[:0-1] Hong Kong; Chan, Bert Wang-Chak (2019-10-15). "Lenia: Biology of Artificial Life". Complex Systems. 28 (3): 251–286. doi:10.25088/ComplexSystems.28.3.251.

[2] "Lenia". chakazul.github.io. Retrieved 2021-10-12.

[3] Roberts, Siobhan (2020-12-28). "The Lasting Lessons of John Conway's Game of Life". The New York Times. ISSN 0362-4331. Retrieved 2021-10-13.

[4] "The virtual creatures competition". virtualcreatures.github.io. Retrieved 2021-10-12.

[5] "ALife Art Award 2018". ALIFE Art Award 2018. Retrieved 2021-10-12.

[6] "Lenia". chakazul.github.io. Retrieved 2021-10-13.

[7] Gilpin, William (2019-09-04). "Cellular automata as convolutional neural networks". Physical Review E. 100 (3): 032402. doi:10.1103/PhysRevE.100.032402. ISSN 2470-0045.

[8] Mordvintsev, Alexander; Randazzo, Ettore; Niklasson, Eyvind; Levin, Michael (2020-02-11). "Growing Neural Cellular Automata". Distill. 5 (2): e23. doi:10.23915/distill.00023. ISSN 2476-0757.

[9] Gilpin, William (2019-09-04). "Cellular automata as convolutional neural networks". Physical Review E. 100 (3): 032402. doi:10.1103/PhysRevE.100.032402. ISSN 2470-0045.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

Search

레니아

네임스페이스

더

목차

규칙.

반복적인 갱신

상태 세트

인근 지역

로컬 규칙

커널 생성

성장 맵핑

게임 오브 라이프

패턴

관련 작업

「」를 참조해 주세요.

외부 링크

레퍼런스

Search

레니아

규칙.

반복적인 갱신

상태 세트

인근 지역

로컬 규칙

커널 생성

성장 맵핑

게임 오브 라이프

패턴

관련 작업

「 」를 참조해 주세요.

외부 링크

레퍼런스

「」를 참조해 주세요.