완충 솔루션

완충액(더 정확히는 pH버퍼 또는 수소이온버퍼)은 약산과 그 결합염기의 혼합물로 이루어진 수용액 또는 그 반대이다.소량의 강한 산이나 염기가 첨가될 때 pH는 거의 변하지 않습니다.완충용액은 다양한 화학용도에서 pH를 거의 일정한 값으로 유지하는 수단으로 사용된다.자연계에는 pH 조절을 위해 완충제를 사용하는 많은 생명계가 있다.예를 들어, 중탄산염 완충 시스템은 혈액의 pH를 조절하기 위해 사용되며, 중탄산염 또한 바다에서 완충제 역할을 한다.

버퍼링의 원리

그림 1알칼리

약산 a (pK =

4.

7

)의 산성용액에 대한 시뮬레이션 적정

완충용액은 약한 산 HA와 그 켤레 염기⁻ A 사이의 화학적 평형 때문에 pH 변화에 저항한다.

HA h⁺ H + A⁻

약산과 그 켤레 염기의 평형 혼합물에 강산을 첨가하면 수소 이온(H⁺)이 첨가되고, 르 샤틀리에 원리에 따라 평형이 왼쪽으로 이동한다.이로 인해 수소이온 농도는 강산첨가량에 비해 예상보다 적게 증가한다.마찬가지로 강한 알칼리를 첨가하면 수소이온 농도는 첨가된 알칼리 양에 대해 예상되는 양보다 낮아진다.그림 1에서는 pK_a = 4.7인 약산을 시뮬레이션하여 적정한 것으로 그 효과를 알 수 있다.비분리산의 상대적 농도는 파란색으로 표시되고, 켤레 염기는 빨간색으로 표시됩니다.pH는 pH = 4.7을 중심으로 한 완충 영역 pH = pK_a ± 1에서 상대적으로 느리게 변화합니다. 여기서 [HA] = [A⁻]입니다.수소 이온 농도는 반응에서 대부분의 첨가된 수산화 이온이 소비되기 때문에 예상보다 감소합니다.

OH⁻ + HA → HO₂ + A⁻

중화 반응(pH의 증가를 초래하는 반응)에서는 소량만 소비된다.

OH⁻ + H⁺ → HO₂.

산이 95% 이상 탈양성자화되면 첨가된 알칼리의 대부분이 중화 반응에서 소비되기 때문에 pH가 빠르게 상승한다.

버퍼 용량

완충용량은 산 또는 알칼리 농도 변화에 대한 완충제를 포함한 용액의 pH 변화에 대한 내성을 정량적으로 측정하는 것이다.다음과 ^[1]^[2]같이 정의할 수 있습니다.

{\displaystyle \displaystyle = dc_{b}}{d(\mathrm {pH}}}},

dC_{b}

서 d

dC_{b}

b(\

displaystyle dC_{b})

는

dC_{b}

극소량의 부가염기 또는

{\displaystyle \displaystyle =-{\frac {dC_{a}}}{d(\mathrm {pH}}}},

dC_{a}

서 d C

dC_{a}

{\

displaystyle dC_{a}}

는

dC_{a}

극소량의 첨가산입니다.pH는 -log₁₀[H⁺]로 정의되며 d(pH)는 pH의 미세한 변화입니다.

어느 정의든 해리 상수_a K를 가진 약한 산 HA의 완충 용량은 다음과 같이 표현될^[3]^[4]^[2] 수 있다.

\displaystyle \displaystyle = 2.display([\ce {H+}})+{\frac {T_{\ce {HA}}}K_{a}[{\ce {H+}}}}}{(K_{a}+[{\ce {H+}}}}}})^{2}}+{\frac {K_{\text{w}}}}{[{\ce {H+}}}}}}}}}}\right},}}

여기서 [H⁺]는 수소 이온

T_{\text{HA}}

이고,

(\

text})는

HA}}}

은

T_{\text{HA}}

첨가된 산의 총 농도입니다.K는_w 물의 자가이온화를 위한 평형상수로 1.0×10과⁻¹⁴ 같다.용액⁺ H는 하이드로늄 이온₃⁺ HO로 존재하며, 하이드로늄 이온의 추가 수분은 매우 높은 산 농도를 제외하고 해리 평형에 무시할 수 있는 영향을 미친다는 점에 유의하십시오.

그림 2pK_a = 7인 약산 0.1M 용액의 완충용량β

이 방정식은 상승 버퍼 용량의 영역이 3개 있음을 나타냅니다(그림2 참조).

곡선의 중앙 영역(그림에서 녹색으로 표시됨)에서는 두 번째 항이 우세합니다. $\displaystyle \beta \약 2.303{\frac {T_{\ce {HA}}}K_{a}[{\ce {H+}}}{(K_{a}+[\ce {H+}}}})^{2}}}.}$ 버퍼 용량은 pH = pK에서_a 로컬 최대값까지 상승합니다.이 피크의 높이는 pK_a 값에 따라 달라집니다.버퍼링제의 농도(HA)가 매우 작고 버퍼링제의 ^[2]농도가 높아짐에 따라 증가하는 경우에는 버퍼 용량이 무시할 수 있다.일부 작성자는 버퍼 ^[1]용량 그래프에 이 영역만 표시합니다.
버퍼 용량은 pH = pK_a ± 1에서 최대값의 33%, pH = pK_a ± 1.5에서 10%, pH = pK_a ± 2에서 1%까지 떨어집니다. 따라서 가장 유용한 범위는 약 pK_a ± 1입니다. 특정 PH에서 사용할 버퍼를 선택할 때 가능한 한 가까운_a 값을 가져야 합니다.
강산성 용액에서는 pH가 약 2보다 작을 경우(그림에서 빨간색으로 표시), 방정식의 첫 번째 항이 우세하며 pH가 감소함에 따라 버퍼 용량이 기하급수적으로 증가합니다. $\displaystyle \beta \약 10^{-\mathrm {pH}}.}$ 이는 두 번째 항과 세 번째 항이 매우 낮은 pH에서 무시할 수 있게 되기 때문이다.이 용어는 버퍼링 에이전트의 유무와는 무관합니다.
강알칼리성 용액에서는 pH가 약 12(그림에서 파란색) 이상이며, 방정식의 세 번째 항이 우세하며, pH가 증가함에 따라 버퍼 용량이 기하급수적으로 증가합니다. $\displaystyle \beta \약 10^{\mathrm {pH} -\mathrm {p}K_{\text{w}}}}.}$ 이것은 첫 번째 항과 두 번째 항이 매우 높은 pH에서 무시할 수 있게 된다는 사실에서 비롯됩니다.이 용어는 버퍼링 에이전트의 유무와도 무관합니다.

버퍼 적용

완충제를 함유한 용액의 pH는 용액에 존재하는 다른 물질에 관계없이 좁은 범위 내에서만 변화할 수 있습니다.생물학적 시스템에서 이것은 효소가 올바르게 기능하기 위한 필수 조건이다.예를 들어 사람의 혈액 중 혈장 분율에는 탄산(HCO
₂
₃)과 중탄산(HCO⁻
₃)의 혼합물이 존재하며, 이는 혈액의 pH를 7.35~7.45 사이로 유지하는 주요 메커니즘을 구성한다.이 좁은 범위(7.40 ± 0.05 pH 단위)를 벗어나면 산증 및 알칼로시스 대사 상태가 빠르게 진행되어 정확한 완충능력이 빠르게 회복되지 않으면 결국 사망에 이르게 된다.

용액의 pH 값이 너무 많이 오르거나 떨어지면, 변성이라고 알려진 과정에서 효소의 효과가 감소하는데, 이것은 보통 돌이킬 ^[5]수 없다.연구에 사용되는 생물학적 샘플의 대부분은 완충 용액, 종종 pH 7.4의 인산염 완충 식염수(PBS)에 보관된다.

산업에서는 완충제가 발효 공정 및 착색 직물에 사용되는 염료의 정확한 조건을 설정하는 데 사용된다.또한 pH 미터의 화학^[4] 분석 및 교정에도 사용됩니다.

단순 버퍼링 에이전트

버퍼링 에이전트	pK_a	유용한 pH 범위
구연산	3.13, 4.76, 6.40	2.1–7.4
아세트산	4.8	3.8–5.8
KH₂PO₄	7.2	6.2–8.2
체이스	9.3	8.3–10.3
붕산염	9.24	8.25–10.25

산영역의 완충제는 염산 등의 강산을 특정 완충제에 첨가함으로써 pH를 원하는 값으로 조정해도 된다.알칼리성 완충제는 수산화나트륨 등의 강염기를 첨가해도 좋다.또, 완충 혼합물은, 산과 그 켤레 베이스의 혼합물로 해도 좋다.예를 들어 아세트산과 아세트산나트륨의 혼합물로 아세트산 완충제를 만들 수 있다.마찬가지로 염기 및 그 복합산의 혼합물로 알칼리 완충제를 만들 수 있다.

"범용" 버퍼 혼합물

pK값의_a 차이가 2개 이하인 물질을 조합하여 pH를 조정함으로써 광범위한 버퍼를 얻을 수 있다.구연산은 3개의 pK_a 값을 가지며 2개 이하로 분리되기 때문에 완충 혼합물의 유용한 성분이다.버퍼 범위는 다른 버퍼링 에이전트를 추가하여 확장할 수 있습니다.다음 혼합물(McIlvaine 완충액)의 완충 범위는 pH 3~8입니다.^[6]

0.2M NaHPO₂₄(mL)	0.1M 구연산(mL)	pH
20.55	79.45	3.0
38.55	61.45	4.0
51.50	48.50	5.0
63.15	36.85	6.0
82.35	17.65	7.0
97.25	2.75	8.0

구연산, 인산단칼륨, 붕산 및 디에틸바르비투르산을 포함한 혼합물을 pH 2.6~^[7]12를 커버할 수 있다.

다른 범용 버퍼로는 1931년에 개발된 Carmody^[8] 버퍼와 Britton-Robinson 버퍼가 있습니다.

생물학에 사용되는 일반적인 완충 화합물

유효 범위는 위의 버퍼 용량을 참조하십시오.

일반명(화학명)	pK_a, 25 °C	Temp. 효과, dpH/dT(K⁻¹)^[9]	몰. 체중
탭, ([트리스(히드록시메틸)메틸아미노]프로판술폰산)	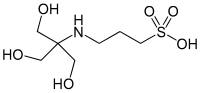8.43	−0.018	243.3
바이신 (2-(비스(2-히드록시에틸)아세트산	8.35	−0.018	163.2
트리스 (트리스(히드록시메틸)아미노메탄) 또는 2-아미노-2-(히드록시메틸)프로판-1, 3-디올)	8.07^[a]	−0.028	121.14
트리신 (N-[트리스(히드록시메틸)메틸]글리신)	8.05	−0.021	179.2
TAPSO, (3-[N-트리스(히드록시메틸)메틸아미노]-2-히드록시프로판술폰산)	7.635		259.3
헤페스 (4-(2-히드록시에틸)-1-글루아진에탄술폰산)	7.48	−0.014	238.3
TES, (2γ[1,3-디히드록시-2-(히드록시메틸)프로판-2-일]에탄술폰산)	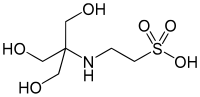7.40	−0.020	229.20
MOPS, (3-(N-모르폴리노)프로판술폰산)	7.20	−0.015	209.3
파이프, (피페라진-N, N--bis(2-에탄술폰산)	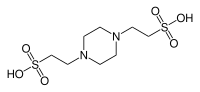6.76	−0.008	302.4
카코딜레이트, (디메틸라센산)	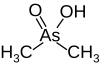6.27		138.0
MES, (2-(N-모르폴리노)에탄술폰산)	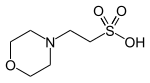6.15	−0.011	195.2

^ Tris는 염기이며, pK_a = 8.07은 결합산을 의미한다.

버퍼 pH 계산 중

단프로톤산

먼저 평형식을 적습니다.

HA a⁻ A + H⁺

이것은 산이 분해되면 동일한 양의 수소 이온과 음이온이 생성된다는 것을 보여준다.이 세 가지 성분의 평형 농도는 ICE 표에서 계산할 수 있다(ICE는 "초기, 변화, 평형"을 나타낸다).

모노프로톤산용 ICE 테이블
	[하하]	[A⁻]	[H⁺]
I	C₀	0	y
C	−x	x	x
E	C₀ − x	x	x + y

I로 표시된 첫 번째 행은 초기 조건을 나열합니다. 산의 농도는 C이며₀, 처음에는 분해되지 않으므로 A와⁺ H의⁻ 농도는 0이 됩니다. y는 염산과 같은 첨가된 강산의 초기 농도입니다.수산화나트륨과 같은 강한 알칼리를 첨가하면 알칼리가 용액에서 수소이온을 제거하기 때문에 y는 음의 부호를 갖게 된다.두 번째 행은 "변경"을 의미하는 C로 표시되어 산이 분리될 때 발생하는 변화를 나타냅니다.산 농도는 -x만큼 감소하고, A와⁻ H의⁺ 농도는 +x만큼 증가한다.이것은 평형식으로 이어집니다."균형"을 의미하는 E로 표시된 세 번째 행은 처음 두 행을 합산하여 평형에서의 농도를 보여준다.

x를 구하려면 농도 측면에서 평형 상수에 대한 공식을 사용합니다.

({displaystyle K_{\text{a}}=frac {{\ce {H+}}}}][{\ce {HA}}}}})}

농도를 ICE 표의 마지막 행에 있는 값으로 대체합니다.

K_{\text{a}}=flac {x(x+y)}{C_{0}-x}}.

심플화

x^{2}+(K_{\text{a}+y})x-K_{\text{a}}C_{0}=0.

C, K_a 및 y에 대한₀ 특정 값을 사용하여 이 방정식은 x에 대해 풀 수 있습니다. pH = -log₁₀[H⁺]라고 가정하면 pH는 pH = -log₁₀(x + y)로 계산될 수 있습니다.

폴리프로틴산

구연산 10밀리몰 용액에 대해 계산된 종(%) 형성

폴리프로틴산은 하나 이상의 양성자를 잃을 수 있는 산이다.첫 번째 양성자의 해리에 대한 상수는 K_a1, 연속 양성자의 해리에 대한 상수는 K 등으로 표시될_a2 수 있다.구연산은 세 개의 양성자를 잃을 수 있기 때문에 폴리프로틴산₃ HA의 한 예이다.

단계적 해리 상수
평형	구연산
HA₃ † HA₂⁻ + H⁺	pK_a1 = 3.13
HA₂⁻ † HA²⁻ + H⁺	pK_a2 = 4.76
HA²⁻ a³⁻ A + H⁺	pK_a3 = 6.40

연속되는_a pK값의 차이가 약 3 미만이면 평형상태에서 종의 pH 범위 사이에 중복이 있다.차이가 작을수록 겹치는 부분이 많아집니다.구연산의 경우 중복이 광범위하고 pH 2.5~7.5의 전 범위에 걸쳐 구연산 용액이 완충된다.

폴리프로틴산에 의한 pH의 계산은 종분화 계산을 실시할 필요가 있다.구연산의 경우, 이는 두 가지 질량 균형 방정식의 용액을 수반한다.

디스플레이 스타일C_{\ce {A}}&=[{\ce {A^3-}}+\beta _{1}[{\ce {H+}}]+\beta _{2}[{\ce {A^3-}}][\ce {A^3-}}}_{\ce {H+}}_{\beta}_{{{\ce {\ce {\}}}_{{{}}_{beta}}\end { aligned}}

C는_A 산의 분석 농도, C는_H 첨가된 수소 이온의_q 분석 농도, β는 누적 결합 상수이다.K는_w 물의 자기 이온화에 대한 상수이다.미지의³⁻ 양 [A]와 [H⁺]에 두 개의 비선형 연립 방정식이 있습니다.이 계산을 위해 많은 컴퓨터 프로그램을 사용할 수 있습니다.구연산 분화도는 HySS ^[10]프로그램으로 제작되었다.

N.B. 누적 전체 상수의 번호는 단계적 해리 상수의 번호 지정의 역수입니다.

트리바산에 대한 누적 연관 상수(β) 값과 단계적 해리 상수(K) 값 사이의 관계.
평형	관계
A³⁻⁺ + H ah²⁺ AH	로그₁ β_a3= pk
A³⁻ + 2H⁺ ah₂⁺ AH	로그₂ β_a2 = log + pk_a3
A³⁻ + 3H⁺₃ † AH	로그₃ β_a1 = pk + pk_a2 + pk_a3

누적 연관 상수는 위의 사양도를 얻기 위해 사용되는 것과 같은 범용 컴퓨터 프로그램에서 사용됩니다.

「」를 참조해 주세요.

레퍼런스

^ ^a ^b ^c Skoog, Douglas A.; West, Donald M.; Holler, F. James; Crouch, Stanley R. (2014). Fundamentals of Analytical Chemistry (9th ed.). Brooks/Cole. p. 226. ISBN 978-0-495-55828-6.
^ ^a ^b ^c Urbansky, Edward T.; Schock, Michael R. (2000). "Understanding, Deriving and Computing Buffer Capacity". Journal of Chemical Education. 77 (12): 1640–1644. Bibcode:2000JChEd..77.1640U. doi:10.1021/ed077p1640.
^ Butler, J. N. (1998). Ionic Equilibrium: Solubility and pH calculations. Wiley. pp. 133–136. ISBN 978-0-471-58526-8.
^ ^a ^b Hulanicki, A. (1987). Reactions of acids and bases in analytical chemistry. Translated by Masson, Mary R. Horwood. ISBN 978-0-85312-330-9.
^ Scorpio, R. (2000). Fundamentals of Acids, Bases, Buffers & Their Application to Biochemical Systems. ISBN 978-0-7872-7374-3.
^ McIlvaine, T. C. (1921). "A buffer solution for colorimetric comparaison" (PDF). J. Biol. Chem. 49 (1): 183–186. doi:10.1016/S0021-9258(18)86000-8. Archived (PDF) from the original on 2015-02-26.
^ Mendham, J.; Denny, R. C.; Barnes, J. D.; Thomas, M. (2000). "Appendix 5". Vogel's textbook of quantitative chemical analysis (5th ed.). Harlow: Pearson Education. ISBN 978-0-582-22628-9.
^ Carmody, Walter R. (1961). "Easily prepared wide range buffer series". J. Chem. Educ. 38 (11): 559–560. Bibcode:1961JChEd..38..559C. doi:10.1021/ed038p559.
^ "Buffer Reference Center". Sigma-Aldrich. Archived from the original on 2009-04-17. Retrieved 2009-04-17.
^ Alderighi, L.; Gans, P.; Ienco, A.; Peters, D.; Sabatini, A.; Vacca, A. (1999). "Hyperquad simulation and speciation (HySS): a utility program for the investigation of equilibria involving soluble and partially soluble species". Coordination Chemistry Reviews. 184 (1): 311–318. doi:10.1016/S0010-8545(98)00260-4. Archived from the original on 2007-07-04.

외부 링크

"Biological buffers". REACH Devices.

[10] Tris는 염기이며, pK_a = 8.07은 결합산을 의미한다.

[Skoog-1] Skoog, Douglas A.; West, Donald M.; Holler, F. James; Crouch, Stanley R. (2014). Fundamentals of Analytical Chemistry (9th ed.). Brooks/Cole. p. 226. ISBN 978-0-495-55828-6.

[Urbansky-2] Urbansky, Edward T.; Schock, Michael R. (2000). "Understanding, Deriving and Computing Buffer Capacity". Journal of Chemical Education. 77 (12): 1640–1644. Bibcode:2000JChEd..77.1640U. doi:10.1021/ed077p1640.

[3] Butler, J. N. (1998). Ionic Equilibrium: Solubility and pH calculations. Wiley. pp. 133–136. ISBN 978-0-471-58526-8.

[Hulanicki-4] Hulanicki, A. (1987). Reactions of acids and bases in analytical chemistry. Translated by Masson, Mary R. Horwood. ISBN 978-0-85312-330-9.

[Scorpio_2000-5] Scorpio, R. (2000). Fundamentals of Acids, Bases, Buffers & Their Application to Biochemical Systems. ISBN 978-0-7872-7374-3.

[6] McIlvaine, T. C. (1921). "A buffer solution for colorimetric comparaison" (PDF). J. Biol. Chem. 49 (1): 183–186. doi:10.1016/S0021-9258(18)86000-8. Archived (PDF) from the original on 2015-02-26.

[7] Mendham, J.; Denny, R. C.; Barnes, J. D.; Thomas, M. (2000). "Appendix 5". Vogel's textbook of quantitative chemical analysis (5th ed.). Harlow: Pearson Education. ISBN 978-0-582-22628-9.

[carmody-8] Carmody, Walter R. (1961). "Easily prepared wide range buffer series". J. Chem. Educ. 38 (11): 559–560. Bibcode:1961JChEd..38..559C. doi:10.1021/ed038p559.

[9] "Buffer Reference Center". Sigma-Aldrich. Archived from the original on 2009-04-17. Retrieved 2009-04-17.

[11] Alderighi, L.; Gans, P.; Ienco, A.; Peters, D.; Sabatini, A.; Vacca, A. (1999). "Hyperquad simulation and speciation (HySS): a utility program for the investigation of equilibria involving soluble and partially soluble species". Coordination Chemistry Reviews. 184 (1): 311–318. doi:10.1016/S0010-8545(98)00260-4. Archived from the original on 2007-07-04.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[a]

[10]

Search

완충 솔루션

네임스페이스

더

목차