이소모르프 이론

수학, 특히 추상대수학에서 이소모르프 이론(Noeter의 이소모르프 이론이라고도 함)은 인용문, 동형문, 아형문자 사이의 관계를 기술하는 이론이다.이론의 버전은 그룹, 고리, 벡터 공간, 모듈, 리 알헤브라스, 그리고 다양한 다른 대수 구조에 존재한다.보편적 대수학에서 이형성 이론은 알헤브라와 합성의 맥락으로 일반화될 수 있다.

역사

1927년 Mathitische Annalen에서 출판된 그녀의 논문 Abstrakter Aufbau der Idealtheori에서 Emmy Needer에 의해 모듈의 동형성에 대한 일반적인 이론들이 공식화되었다.이러한 이론의 덜 일반적인 버전은 리차드 데데킨드의 연구와 노에더의 이전 논문에서 찾을 수 있다.

3년 후, B.L. 반 데어 웨르덴은 그의 영향력 있는 Moderne 대수학 교과서를 처음으로 출판했는데, 이 교과서에 그룹-링-필드 접근법을 채택했다.반 데어든은 아르틴, 빌헬름 블래쉬케, 오토 슈라이어, 반 데어 바어든이 진행하는 세미나뿐만 아니라 그룹 이론에 대한 노에더와 대수학에 대한 에밀 아르틴의 강의를 주요 참고 자료로 인정했다.동형주의 정리라고 하는 3가지 이형주의 이론과 그룹에 적용할 때 2가지 이형주의 법칙이 명시적으로 나타난다.

무리

우리는 먼저 그 집단의 이소형성 이론들을 제시한다.

번호 및 이름에 대한 참고 사항

아래에는 A, B, C, D라는 네 가지 이론이 제시되어 있다.그것들은 종종 "제1차 이형성 정리", "제2차.."로 번호가 매겨진다.「」등등. 그러나, 번호 매기기에 관한 보편적인 합의는 없다.여기서 우리는 문헌에서 집단 이형주의 이론의 몇 가지 예를 제시한다.이러한 이론에는 링과 모듈의 유사성이 있다는 점에 유의하십시오.

집단 이형성 이론의 명칭 비교

댓글	작가	정리 A	정리 B	정리 C
"제3"의 정리 없음	제이콥슨[1]	동형성의 기본 정리	(제2차 이형성 정리)	"제1차 이형성 정리라고 불리는 것"
	반 데어 웨르덴,[2] 더빈[4]	동형성의 기본 정리	제1차 이형성 정리	제2차 이형성 정리
	크냅[5]	(이름 없음)	제2차 이형성 정리	제1차 이형성 정리
	그릴렛[6]	동형성 정리	제2차 이형성 정리	제1차 이형성 정리
세 개의 숫자 정리	(그릴레트당 기타 관례)	제1차 이형성 정리	제3차 이형성 정리	제2차 이형성 정리
	로트맨[7]	제1차 이형성 정리	제2차 이형성 정리	제3차 이형성 정리
	프랄리[8]	(이름 없음)	제2차 이형성 정리	제3차 이형성 정리
	더미트 & 풋[9]	제1차 이형성 정리	두 번째 또는 다이아몬드 이형성 정리	제3차 이형성 정리
번호 매기기 금지	밀네[10]	동형성 정리	이소모르프 정리	대응 정리
	스콧[11]	동형성 정리	이소모르프 정리	신입생 정리

보통 격자 정리나 대응 정리라고 알려진 정리 D를 이등형 정리 중 하나에 포함하는 것은 덜 일반적이지만, 그럴 때는 마지막이다.

정리 명세서

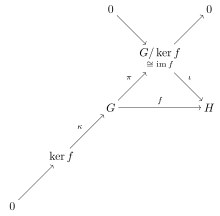
정리 A(그룹)

G와 H를 집단이 되게 하고, f : G → H를 동형상주의로 한다.다음:

1. f의 낟알은 G의 정상적인 부분군이다.
2. f의 이미지는 H의 부분군이며,
3. f의 이미지는 지수 그룹 G / ker(f)에 이형적이다.

특히 f가 허탈적이라면 H는 G / ker(f)에 대해 이형성이다.

정리 B(그룹)

$G{\displaystyle }$ ${\displaystyle G}$을(를) 그룹화하십시오$$.$S{\displaystyle }$ ${\displaystyle S}$을(를) $G{\displaystyle }$ ${\displaystyle G$의 하위 그룹으로 하고$$ N ${\displaystyle N}$을(를) $G{\displaystyle }$ ${\displaystyle G}$의 일반 하위 그룹으로$$ 한다$.$ 그런 다음 다음을 유지하십시오.

1. $제품{\displaystyle }$ ${\displaystyle S}$ N$${\$displaystyle$SN}은(는$)$ G {\$displaystyle$ G$}$의 하위 그룹이다$.$
2. 교차로 $S{\displaystyle }$ ${\displaystyle \cap }$ ${\displaystyle N}$ ${\displaystyle S\cap N}$은(는) $S{\displaystyle }$ ${\displaystyle S}$의 정규 부분군이며$,$
3. ${\displaystyle 지수}$ 그룹$({\displaystyle S}$ ${\displaystyle N}$)${\displaystyle }$/ N ${\displaystyle (SN)/N}$ 및 $S$ /${\displaystyle }$( ${\displaystyle S}$ ${\displaystyle \cap }$ ${\displaystyle N}$) ${\displaystyle S/(S\cap$ N$)}$은 이형이다$$.

Technically, it is not necessary for ${\displaystyle N}$ to be a normal subgroup, as long as ${\displaystyle S}$ is a subgroup of the normalizer of ${\displaystyle N}$ in ${\displaystyle G}$. In this case, the intersection ${\displaystyle S\cap N}$ is not a normal subgroup of ${\displaystyle G}$, 그러나 그것은 여전히 $S$의 $정상적인 부분군$이다$.$

이 정리를 이형성 정리,^[10] 다이아몬드 정리^[12] 또는 평행사변형 정리라고 부르기도 한다.^[13]

An application of the second isomorphism theorem identifies projective linear groups: for example, the group on the complex projective line starts with setting ${\displaystyle G=\operatorname {GL} _{2}(\mathbb {C} )}$, the group of invertible 2 × 2 complex matrices, ${\displaystyle S=\operato$$rname {SL} _{2}(\mathb {C}$ $),$ $결정{\displaystyle }$ 요인 1개의 행렬의 부분군 및 N ${\displaystyle N}$ 스칼라 ={( )의$$ 부분군 C ${\$$I=\left\{\left({\begin{smallmatrix}a&0\\0&a\end{smallmatrix}}\right):a\in \mathbb {C} ^{\times }\right\}}$, we have ${\displaystyle S\cap N=\{\pm I\}}$, where ${\displaystyle I}$ is the identity matrix, and ${\displaystyle SN=\operatorname {GL} _{2}(\mathbb {C} )}$.그 후 두 번째 이형성 정리에서는 다음과 같이 기술하고 있다.

${\displaystyle \operatorname {PGL} _{2}(\mathb {C} ) _{2}\left(\mathb {C} )/(\mathb {C} ^{\times }\!I\rig)\cong \operatorname {SL} _{2}(\mathb {C} )/\\\pm I\}=:\operatorname {PSL} _{2}(\mathb {C} )}$

정리 C(그룹)

$G{\displaystyle }$ ${\displaystyle G}$을(를) 그룹으로$$ 하고, $N{\displaystyle }$ ${\displaystyle N}$을(를) $G{\displaystyle }$ ${\displaystyle G}$의 일반 하위 그룹으로 한다$.$ 그런 다음

1. $K{\displaystyle }$ ${\displaystyle K}$이(가$)$ ${\displaystyle N}$ ${\displaystyle \subseteq }$ K ${\displaystyle \subseteq }$ ${\displaystyle G}$ ${\displaystyle G}과(와$) 같은 G$$${\$$displaystyle$ $G}$의 부분군인 $경우{\displaystyle }$ $G{\displaystyle }$$$/ N {\$displaystyle G/N}$과(와)의 부분군 $이형성$이 있다$$$.$
2. ${\displaystyle G}$/ ${\displaystyle N}$ ${\displaystyle G/N}$의 모든 부분군은 $G{\displaystyle }$ ${\$$displaystyle$ ${\displaystyle G}$$}$의 일부 $부분군{\displaystyle }$ K ${\displaystyle K}$에 대해$$ $K{\displaystyle }$/ ${\displaystyle N}$ ${\$$displaystyle K/N}$ 형식이다$.$
3. $K{\displaystyle }$ ${\displaystyle K}$이$($가) ${\displaystyle N}$${\displaystyle }$${\displaystyle \subseteq }$ K ${\displaystyle \subseteq }$ ${\displaystyle G}$ ${\displaystyle G}$과(와) 같은 G ${\$$displaystyle G}$의 정규 부분군인 경우 G / N ${\$$displaystyle G/N}$과($)$의 $정규{\displaystyle }$ 부분군 이형성을 ${\displaystyle 갖는다}$.
4. ${\displaystyle G}$${\displaystyle }$/ ${\displaystyle N}$ ${\displaystyle$ G$/N}$의 모든 정상 부분군은 $G{\displaystyle }$ ${\$$displaystyle$ ${\displaystyle G}$$}$의 일부 정상 $부분군{\displaystyle }$ K ${\displaystyle K}$에 대해$$ $K{\displaystyle }$/ ${\displaystyle N}$ ${\$$displaystyle K/N}$ 형식이다$.$
5. If ${\displaystyle K}$ is a normal subgroup of ${\displaystyle G}$ such that ${\displaystyle N\subseteq K\subseteq G}$, then the quotient group ${\displaystyle (G/N)/(K/N)}$ is isomorphic to ${\displaystyle G/K}$.

정리 D(그룹)

대응 정리(격자 정리라고도 한다)를 제3 또는 제4의 이소모르프 정리라고도 한다.

자센하우스의 보조정리(나비 보조정리라고도 한다)는 제4차 이형성 정리라고도 한다.^[14]

토론

첫 번째 이형성 정리는 집단의 범주가 (정상 epi, mono)-요인화 가능하다고 하여 범주 이론 언어로 표현할 수 있다. 즉, 정상 인식과 단형성은 범주에 대한 인자화 체계를 형성한다.$이$는 형태론 f${\displaystyle }$: ${\displaystyle G}$→ ${\displaystyle H}$ ${\displaystyle$ f$:$$G\rightarrow H}$도표는 그룹 카테고리의 모든 형태론은 범주의 이론적 의미에 커널이 있음을 보여준다; 임의의 형태주의 f 인자는 ${\displaystyle \mathrm{into}}$ ${\displaystyle \circ }$ {$${ { { { \$iota \circpi$}으로$,$ 여기서 ι은 단형주의, π은 인식주의(동형 범주에서 모든 인식은 정상이다.이것은 도표에서 물체 ${\displaystyle \ker }$upper ${\displaystyle f}$ ${\displaystyle \ker f}$와 단형주의 $\kappa {\displaystyle }$: ${\displaystyle \ker }$ ${\displaystyle }$ f${\displaystyle }$→ G ${\displaystyle \kappa :\ker f\오른쪽 화살표$ G$}($커널은 항상 단형체)로 표시되며, 도표의 왼쪽 하단에서 오른쪽 상단으로 흐르는 짧은 정확한 시퀀스를 완성한다.정확한 시퀀스 규약을 사용하면 ${\displaystyle \ker }$ ${\displaystyle }$ ${\displaystyle f}${\$displaystyle \ker$f}에서 $H{\displaystyle }$ ${\displaystyle H},$ $G$ / ${\displaystyle \ker }$ ${\displaystyle }$ ${\displaystyle f}$ ${\displaystyle$ G$/\ker f}$까지 영점 형태론을 그릴 필요가 없게 된다$.$

If the sequence is right split (i.e., there is a morphism σ that maps ${\displaystyle G/\operatorname {ker} f}$ to a π-preimage of itself), then G is the semidirect product of the normal subgroup ${\displaystyle \operatorname {im} \kappa }$ and the subgroup ${\displaystyle \operatorname {im} \sigma }$.If it is left split (i.e., there exists some ${\displaystyle \rho :G\rightarrow \operatorname {ker} f}$ such that ${\displaystyle \rho \circ \kappa =\operatorname {id} _{{\text{ker}}f}}$), then it must also be right split, and ${\displaystyle \operatorname {im} \kappa \times \$연산자 $이름 {im} \sigma }$은(는) G의 직접 제품 분해물이다.일반적으로 오른쪽 $분할$의 존재는 왼쪽 분할의 존재를 의미하지는 않지만, 아벨리아 범주(아벨리아 그룹의 분할과 같은)에서 왼쪽 분할과 오른쪽 분할은 분할 보조정리(diving $lema)$에 의해 동등하며, 오른쪽 분할은 직접적인 합계분해를 ${\displaystyle \mathrm{만들기}}$에 충분하다$.$$pa \oplus \operatorname {im} \sigma }$. In an abelian category, all monomorphisms are also normal, and the diagram may be extended by a second short exact sequence ${\displaystyle 0\rightarrow G/\operatorname {ker} f\rightarrow H\rightarrow \operatorname {coker} f\rightarrow 0}$.

두 번째 이형성 정리에서 제품 SN은 G의 부분군 격자에서 S와 N의 결합이고, 교차점 S ∩ N은 충족이다.

세 번째 이형성 정리는 아벨의 범주에 대한 9개의 보조정리, 그리고 물체들 사이의 더 일반적인 지도에 의해 일반화된다.

반지.

링에 대한 이론의 문구는 정상 부분군의 개념이 이상 개념으로 대체되는 것과 유사하다.

정리 A(링)

R과 S를 링으로 하고, and : R → S를 링 동형성으로 한다.다음:

1. φ의 알맹이는 R의 이상이다.
2. φ의 이미지는 S의 서브링이며,
3. φ의 이미지는 지수 링 R/커(φ)에 이형적이다.

특히 φ이 허탈적인 경우, S는 R / ker(φ)에 대해 이형성이 있다.

정리 B(링)

R을 링이 되게 하라.S를 R의 서브링으로 하고, 내가 R의 이상이 되게 하라.다음:

1. S + I = {s + i s ∈ S, i ∈ I }의 합은 R의 하위 문자열이다.
2. 교차로 S ∩ I은 S의 이상이며,
3. 지수 반지(S + I) / I와 S / (S ∩ I)는 이형성이다.

정리 C(링)

R을 반지로 하고, 나는 R의 이상이다.그러면

1. $A{\displaystyle }$ ${\displaystyle A$$}$이${\displaystyle (}$가) ${\displaystyle R}$ ${\displaystyle I\subseteq A}$과$($$와{\displaystyle )}$ 같은$$R ${\$displaystyle R}의 하위 문자열인$$ 경우 A/${\displaystyle I}$ ${\displaystystyle A/I}$은($와$)의 하위 문자열이다$.$
2. $R{\displaystyle }$${\displaystyle /I}$ ${\displaystyle R/I}$의 모든 하위 링은 R의 일부$$ $하위{\displaystyle }$ 링 A$${\$displaystyle A$$/$$I$}에 대한$$ $A{\displaystyle /I}$ ${\displaystyle$A/I$}$ 형식이며$$, $따라서$ I ${\displaystyle \subseteq }$ ${\displaystyle A}$ ${\displaystyle \subseteq }$ ${\displaystyle R}$ ${\displaystystyle I\seteq$ A$\subseteq R$
3. $J{\displaystyle }$${\displaystyle J$$}$이(가) ${\displaystyle R}$ ${\displaystyle$ I\$subseteq$J$}과(와$) 같은 R {\$displaystyle$ R}의 $이상$이라면 J$/$$I$ ${\$displaystyle J/I}은$($와$)$의 ${\displaystyle 이상}$이다$.$
4. $R{\displaystyle /I}$ ${\displaystyle R/I}$의 모든 이상은 ${\displaystyle J/}$${\displaystyle I}$ {\$displaystyle J$$}$에 대해$$ $J{\displaystyle }$/I ${\displaystyle$ J} 형식의 R$$ $displaystyle I {\subseteq J\subseteq R}$과 같이$$ R$}$의 어떤 이상 J ${\$displaysty$}$이다$.$
5. If ${\displaystyle J}$ is an ideal of ${\displaystyle R}$ such that ${\displaystyle I\subseteq J\subseteq R}$, then the quotient ring ${\displaystyle (R/I)/(J/I)}$ is isomorphic to ${\displaystyle R/J}$.

정리 D(링)

Let ${\displaystyle I}$ be an ideal of ${\displaystyle R}$. The correspondence ${\displaystyle A\leftrightarrow A/I}$ is an inclusion-preserving bijection between the set of subrings ${\displaystyle A}$ of ${\displaystyle R}$ that contain ${\displaystyle I}$ and the set of subrings of ${\displaystyle R}$${\displaystyle /}$ ${\displaystyle I}$ ${\displaystyle R/I$ 게다가 A ${\$$displaystyle I}$을$($를$)$ 포함하는 $서브링$으로 A${\displaystyle /I}$ ${\displaystyle A/I}$이($가{\displaystyle }$) $R{\displaystyle /I}$ ${\displaystyle$ R/$I}$의 이상일 경우에만 R {\$displaystystystyle R$$}$의 이상이다$.$^[15]

모듈

모듈들에 대한 이형성 이론의 문장은 특히 간단하다. 왜냐하면 어떤 하위 모듈에서든 지수 모듈을 형성할 수 있기 때문이다.벡터 공간(필드 위의 모듈)과 아벨리아 그룹($Z{\displaystyle \mathbb{}}$ ${\$에 대한 이형성 이론은 이러한 특수한 경우들이다.유한 차원 벡터 공간의 경우 이러한 모든 이론은 순위-적합성 정리에서 따른다.

다음에서 "모듈"은 일부 고정 링 R에 대해 "R-모듈"을 의미한다.

정리 A(모듈)

M과 N을 모듈로 하고, φ : M → N을 모듈 동형성으로 한다.다음:

1. φ의 낟알은 M의 하위 모듈이다.
2. φ의 이미지는 N의 서브모듈이며,
3. φ의 이미지는 지수 모듈 M/커(φ)에 이형이다.

특히 φ이 허탈적인 경우, N은 M / ker( to)에 대해 이형성이 있다.

정리 B(모듈)

M을 모듈로 하고, S와 T를 M의 하위 모듈로 한다.다음:

1. S + T = {s + t s ∈ S, t ∈ T} 합계는 M의 하위 모듈이다.
2. 교차로 S ∩ T는 M의 서브모듈이며,
3. 지수 모듈(S + T) / T 및 S / (S ∩ T)는 이형성이다.

정리 C(모듈)

M을 모듈로 하고, T를 M의 하위 모듈로 한다.

1. $S{\displaystyle }$ ${\displaystyle S}$이(가) ${\displaystyle T}$ ${\displaystyle \subseteq }$ ${\displaystyle S}$ ${\displaystyle \subseteq }$ M ${\displaystyle T\subseteq S\subseteq$ M$}$과$($와) 같은 $M{\displaystyle }$ ${\displaystystyle$$$S$/T$}의 하위 모듈인 $경우{\displaystyle }$${\displaystyle ,}$ S$$/$$T {\$displaystyle M/T}$의 하위 모듈이다$.$
2. $M{\displaystyle /T}$ ${\displaystyle M/$$T}$의 모든$$ 하위 $모듈$은 $T$ ${\displaystyle \subseteq }$ ${\displaystyle S}$ ${\displaystyle \subseteq }$ ${\displaystyle M}$ $\$$$$M$ {\$displaystyle S}$에${\displaystyle 대해}$ S$/T$ {\$displaystyle S/T$$}$ 형식이다$.$
3. If ${\displaystyle S}$ is a submodule of ${\displaystyle M}$ such that ${\displaystyle T\subseteq S\subseteq M}$, then the quotient module ${\displaystyle (M/T)/(S/T)}$ is isomorphic to ${\displaystyle M/S}$.

정리 D(모듈)

Let ${\displaystyle M}$ be a module, ${\displaystyle N}$ a submodule of ${\displaystyle M}$. There is a bijection between the submodules of ${\displaystyle M}$ that contain ${\displaystyle N}$ and the submodules of ${\displaystyle M/N}$. The correspondence is given by ${\display$$style A\leftrightarrow A/N}$ for all ${\displaystyle A\supseteq N}$. This correspondence commutes with the processes of taking sums and intersections (i.e., is a lattice isomorphism between the lattice of submodules of ${\displaystyle M/N}$ and the lattice of submodules of ${\displaystyle M}$ that contain ${\displaystyle N}$$(\displaystyle N}$ $$^[16])

유니버설 대수학

이를 보편적 대수학으로 일반화하려면 정상 하위군을 일치 관계로 대체할 필요가 있다.

대수 $A{\displaystyle }$ ${\displaystyle A}$에 대한 합치는 $등가{\displaystyle }$ 관계 $\phi {\displaystyle \mathrm{}}$ ${\displaystyle A}$ ${\displaystyle \times }$ ${\displaystyle A}$ × A ${\$$displaystyle$ $\Phi \subseteq A$$\times$$$$A}$의 하위 대수(subalgebra)를 형성하는$$$$ 등가성 관계 ${\displaystyle \times }$이다.대리인을 통해 연산을 정의함으로써 등가 $등급{\displaystyle }$ A /${\displaystyle \phi \mathrm{}}$ ${\displaystyle$ A$/\Phi }$을(를) 동일한 유형의 대수 집합으로$$ 만들 수 있다. $이$는 { ${\$$displaystyle \Phi$ $}$이(가$)$ $A{\displaystyle }$ ${\displaystyle \times }$의 하위 대수이므로 잘 정의될 것이다$.$ 결과 $구조$는 대수학이다.

정리 A(범용 대수학)

${\displaystyle f}$: A${\displaystyle }$→ B ${\displaystyle f:$$A\rightarrow B}$은(는) 대수적 동형상이다.Then the image of ${\displaystyle f}$ is a subalgebra of ${\displaystyle B}$, the relation given by ${\displaystyle \Phi :f(x)=f(y)}$ (i.e. the kernel of ${\displaystyle f}$) is a congruence on ${\displaystyle A}$, and the algebras ${\displaystyle A/\Phi }$ and ${\displaystyle \mathrm{im}f}$${\displaystyle \operatorname {im}f}$ 그룹의 경우$$ ${\displaystyle f}$ ( $x{\displaystyle }$ )${\displaystyle }$= f${\displaystyle }$(${\displaystyle y}$) ${\displaystyle f(x)=f(y)}$ ${\displaystyle {}^{}}$ f ( x - 1 ) =${\displaystyle 1^{}}$ $displaystystyle f(xy^{-1})=1$ 따라서 그룹 이론에 사용된 커널 개념을 회복한다.

정리 B(범용 대수)

Given an algebra ${\displaystyle A}$, a subalgebra ${\displaystyle B}$ of ${\displaystyle A}$, and a congruence ${\displaystyle \Phi }$ on ${\displaystyle A}$, let ${\displaystyle \Phi _{B}=\Phi \cap (B\times B)}$ be the trace of ${\displaystyle \Phi }$ in ${\displ$$aystyle B}$과$({\displaystyle 와}$) [${\displaystyle {B\mathrm{}}^{}}$ ${\displaystyle {}^{}}$ ]${\displaystyle {}^{}}$=${\displaystyle }${ ${\displaystyle K/}$ ${\displaystyle A\mathrm{}}$ /${\displaystyle }$∩${\displaystyle }$: ${\displaystyle K}$ ≠ B ${\displaystyle \ne }$ ∅ ${\displaystyle \mathrm{\}}}$ } }${\displaystyle }$} ${\displaystyle [B]^{\\$$Phi }=\{K\in A/\Phi :K\cap B\neq \emptyset \}}$$B{\displaystyle }$ ${\displaystyle$ B$}$와 교차하는 동등성 클래스의 모음$$$.$ 그러면

1. ${\displaystyle {\mathrm{\phi }}_{}}$ ${\displaystyle B_{}}$ ${\$은(는$)$ B {\$displaystyle$ B$}$에 조합된 것이다$.$
2. ${\$$Phi }}$은(는)${\displaystyle A\mathrm{}}$ / {$${\$displaystyle$ A$/\Phi$의 하위골격이다.
3. ${\displaystyle {대수\mathrm{}}^{}}$ $[{\displaystyle B{}^{}}$] ] ${\$$Phi }}$은 대수 $B{\displaystyle }$ /${\displaystyle \phi {\mathrm{}}_{}}$ ${\displaystyle B_{}}$ ${\$ B$/\$에 이형이다.$피 _{B}}$.

정리 C(범용 대수학)

Let ${\displaystyle A}$ be an algebra and ${\displaystyle \Phi ,\Psi }$ two congruence relations on ${\displaystyle A}$ such that ${\displaystyle \Psi \subseteq \Phi }$. Then ${\displaystyle$$\Phi /\Psi =\{([a']_{\Psi },[a'']_{\Psi }):(a',a'')\in \Phi \}=[\ ]_{\Psi }\circ \Phi \circ [\ ]_{\Psi }^{-1}}$ is a congruence on ${\displaystyle A/\Psi }$, and ${\displaystyle A/\Phi }$ is isomorphic to ${\displaystyle (A/\Psi )/(\Phi /\Psi ).$$}$

정리 D(범용대수학)

${\$$displaystyle$ $A}$을(를) 대수학으로 하고$$ ${\displaystyle \mathrm{Con}}$ con${\displaystyle A}$ ${\displaystyle \operatorname {Con}$$}$에 있는 모든$$ 합치 집합을 가리킨다$.$설정된 ${\displaystyle \mathrm{Con}a}$ A$${\$displaystyle \operatorname {Con} A$}은$$(는) 포함에 의해 정렬된 완전한 격자다.^[17]$\phi {\displaystyle \mathrm{}}$ ${\displaystyle \in }$ ${\displaystyle \mathrm{Con}}$ ⁡ ${\displaystyle \mathrm{Con}}$ ${\displaystyle }$ A ${\displaystyle \Phi \in \operatorname {Con} A}$이(가) 합치된 경우$$ [${\displaystyle \phi }$, A ${\displaystyle \times }$ ${\displaystyle A}$ ]${\displaystyle ]}$ ${\displaystyle \mathrm{Con}}$ $⁡$ {\$displaystystyle \left[\]$로 표시된다.$Phi{\displaystyle \mathrm{}}$$,A\times A\right]\subseteq \operatorname {Con}$$\displaystyle \$${\displaystyle \mathrm{Phi}}$ $}$을($$를${\displaystyle )}$ $포함$하는 모든 조합 집합$$(${\displaystyle 예}$:${\displaystyle }$[${$, A × A ] {\$displaystysty$\$left$[\\\])$Phi ,A\times A\right]}$ is a principal filter in ${\displaystyle \operatorname {Con} A}$, moreover it is a sublattice), then the map ${\displaystyle \alpha :\left[\$$Phi ,A\times A\right]\to \operatorname {Con}($A/\$Phi ),\PSI$ \$mapsto \$Psi /\Phi $}$은(는) 격자 이형성이다.^[18][19]

참고

참조

• 에미 노에더, 아브스트라크터 아우프바우 데르 이데오토리(대수학) 자흘- 언 펑크티멘코르펜, 수학자 안날렌 96페이지(1927) 26~61페이지
• 콜린 맥라티 "에메 노에더의 '세트의 이론적' 토폴로지:데데킨드에서 펑커스의 출현에 이르기까지"현대 수학의 건축: 역사와 철학에 관한 에세이 (제레미 그레이와 호세 페레이로스 편집), 옥스퍼드 대학 출판부 (2006) 페이지 211–35.
• Jacobson, Nathan (2009), Basic algebra, vol. 1 (2nd ed.), Dover, ISBN 9780486471891
• Paul M. Cohn, Universal 대수학, II.3 페이지 57
• Milne, James S. (2013), Group Theory, 3.13
• van der Waerden, B. I. (1994), Algebra, vol. 1 (9 ed.), Springer-Verlag
• Dummit, David S.; Foote, Richard M. (2004). Abstract algebra. Hoboken, NJ: Wiley. ISBN 978-0-471-43334-7.
• Burris, Stanley; Sankappanavar, H. P. (2012). A Course in Universal Algebra (PDF). ISBN 978-0-9880552-0-9.
• W. R. Scott (1964), Group Theory, Prentice Hall
• John R. Durbin (2009). Modern Algebra: An Introduction (6 ed.). Wiley. ISBN 978-0-470-38443-5.
• Anthony W. Knapp (2016), Basic Algebra (Digital second ed.)
• Pierre Antoine Grillet (2007), Abstract Algebra (2 ed.), Springer
• Joseph J. Rotman (2003), Advanced Modern Algebra (2 ed.), Prentice Hall, ISBN 0130878685