픽의 확산 법칙

미시적이고 거시적인 관점에서 분자 확산. 처음에는 장벽의 왼쪽에 용질 분자가 있고 오른쪽에는 아무 것도 없습니다. 장벽이 제거되고 용질이 확산되어 용기 전체를 채웁니다. 맨 위: 하나의 분자가 무작위로 움직입니다. 중간: 분자가 많아지면 용질이 점점 더 균일하게 용기에 채워지는 경향이 뚜렷해집니다. 아래: 엄청난 수의 용질 분자에서는 무작위성을 감지할 수 없습니다. 용질은 고농도 영역에서 저농도 영역으로 원활하고 체계적으로 이동하는 것으로 보입니다. 이 매끄러운 흐름은 픽의 법칙에 의해 설명됩니다.

Fick의 확산 법칙은 확산을 설명하며, 1855년 Adolf Fick에 의해 크게 실험적인 결과에 기초하여 처음으로 제시되었습니다. 이들은 확산 계수 $D$ 를 푸는 데 사용될 수 있습니다. 픽의 제1법칙은 확산 방정식과 동일한 그의 제2법칙을 도출하는 데 사용될 수 있습니다.

피크의 법칙을 따르는 확산 과정을 정상 확산 또는 피키안 확산이라고 하며, 그렇지 않으면 비정상 확산 또는 비피키안 확산이라고 합니다.

역사

1855년, 생리학자 아돌프 픽은 확산 수단을 통한 질량 수송을 관장하는 그의 잘 알려진 법칙을 처음으로^[1] 보고했습니다. 픽의 연구는 픽이 유명해질 근본적인 법칙을 제안하는 데 실패한 토마스 그레이엄의 초기 실험에서 영감을 얻었습니다. 픽의 법칙은 다른 저명한 과학자들에 의해 같은 시대에 발견된 관계와 유사합니다. 다아시의 법칙(수압 흐름), 옴의 법칙(전하 수송), 푸리에의 법칙(열 수송).

Fick의 실험(Graham's 모델)은 물의 튜브를 통해 두 저장소 사이에 확산되는 소금의 농도와 플럭스를 측정하는 것을 다루었습니다. Fick의 연구는 주로 유체에서의 확산에 관한 것이었는데, 그 당시에는 고체에서의 확산이 일반적으로 가능하지 않은 것으로 여겨졌기 때문입니다.^[2] 오늘날 픽의 법칙은 고체, 액체 및 기체에서의 확산에 대한 우리의 이해의 핵심을 형성합니다. (후의 두 경우에는 벌크 유체 운동이 없는 경우) 확산 과정이 Fick의 법칙을 따르지 않는 경우(다공성 매질을 통한 확산과 팽윤 관통자 등의 확산의 경우에 발생함),^[3]^[4] 이를 Non-Fickian이라고 합니다.

픽의 제1법칙

Fick의 제1법칙은 확산 플럭스와 농도의 구배를 연관시킵니다. 플럭스는 농도 구배(공간 도함수)에 비례하는 크기로 고농도 영역에서 저농도 영역으로 이동한다고 가정하고, 또는 단순한 용어로 용질이 농도 구배를 가로질러 농도가 높은 영역에서 농도가 낮은 영역으로 이동한다는 개념입니다. 한 (공간적) 차원에서 법칙은 다양한 형태로 작성될 수 있으며, 가장 일반적인 형태(참조^[5]^[6])는 어금니 기반입니다.

J=-D{\frac {d\varphi}{dx}

어디에

$J$ 는 확산 플럭스이며, 그 치수는 단위 시간당 단위 면적당 물질의 양입니다. $J$ 는 단위 시간 간격 동안 단위 영역을 통과할 물질의 양을 측정합니다.
$D$ 는 확산 계수 또는 확산율입니다. 치수는 단위 시간당 면적입니다.
${\frac {d\varphi }{dx}}$ d x ${\displaystyle {\frac$ {d $\v$ dx}}는 농도 구배입니다.
$φ$ (이상적인 혼합물의 경우)는 단위 부피당 물질의 양의 차원을 갖는 농도입니다.
$x$ 는 위치이며, 치수는 길이입니다.

$D$ 는 확산 입자의 속도 제곱에 비례하며, 이는 온도, 유체의 점도 및 Stokes-Ainstein 관계에 따른 입자의 크기에 따라 달라집니다. 묽은 수용액에서 대부분의 이온의 확산 계수는 유사하며 실온에서 (0.6–2)×10 m⁻⁹/s² 범위의 값을 갖습니다. 생물 분자의 경우 확산 계수의 범위는 일반적으로 10⁻¹⁰~10m⁻¹¹²/s입니다.

2차원 이상에서 우리는 1차 도함수를 일반화하는 del 또는 gradient 연산자인 ∇를 사용해야 합니다.

\mathbf {J} =-D\nabla \varphi

여기서 $J$ 는 확산 플럭스 벡터를 나타냅니다.

1차원 확산의 원동력은 양-∂φ/ ∂x이며, 이상적인 혼합물의 경우 농도 구배입니다.

제1법칙의 변형

첫 번째 법칙의 또 다른 형태는 기본 변수를 질량 분율( $예$ 를_i 들어 kg/kg으로 표시)로 사용하는 것입니다. 그러면 방정식은 다음과 같이 바뀝니다.

\mathbf {J} _{i}=-{\frac {\rho D}{M_{i}}\nablay_{i}

어디에

index $i$ 는 i번째 종을 나타냅니다.
$J$ 는_i i번째 종의 확산 플럭스 벡터입니다(예를 들어 mol/m-s²).
$M$ 은_i i번째 종의 몰 질량이고,
$ρ$ 은 혼합물 밀도(예: kg/m)입니다.

ρ $\rho$ {\ $displaystyle$ \rho}이(가) 그래디언트 연산자 외부에 있습니다. 그 이유는 다음과 같습니다.

y_{i}={\frac {\rho_{si}}{\rho}

$여기$ 서 ρ은 i번째 종의 부분 밀도입니다.

이 외에도 이상적인 용액이나 혼합물 이외의 화학 시스템에서는 각 종의 확산을 위한 원동력은 이 종의 화학적 전위의 구배입니다. 그러면 Fick의 첫 번째 법칙(일차원적인 경우)이 작성될 수 있습니다.

J_{i}=-{\frac {Dc_{i}}{RT}}{\frac {\partial \mu _{i}}{\partial x}}

어디에

i번째 종을 나타내는 인덱스 $i$ .
$c$ 는 농도(mol/m³)입니다.
$R$ 은 범용 가스 상수(J/K/mol)입니다.
$T$ 는 절대온도(K)입니다.
$μ$ 는 화학 퍼텐셜(J/mol)입니다.

픽 법칙의 원동력은 도망의 차이로 표현할 수 있습니다.

J_{i}=-{\frac {D}{RT}}{\frac {\partial f_{i}}{\partial x}}

Fugacity $f_{i}$ ${\$ 에 Pa 단위가 있습니다 $f_{i}$ . $f_{i}$ ${\$ 는 $f_{i}$ $증기$ $f_{i}^{\text{G}}$ $f_{i}^{\text{G}}$ ${\$ $G}}$ 또는 $f_{i}^{\text{G}}$ 액체 $f_{i}^{\text{L}}$ ${\$ $L}}$ 단계입니다 $f_{i}^{\text{L}}$ . 증기 액체 평형에서 증발 플럭스는 $f_{i}^{\text{G}}=f_{i}^{\text{L}}$ $f_{i}^{\text{G}}=f_{i}^{\text{L}}$ = $fil$ {\ $displaystyle$ f_{i}^{\ $text{$ $G}}=f_{i}^{\text{$ $L$

피크의 기체 제1법칙 유도

쌍성기체 혼합물에 대한 피크의 법칙의 네 가지 버전이 아래에 제시되어 있습니다. 이러한 가정은 열 확산은 무시할 수 있고, 단위 질량당 신체 힘은 두 종 모두에서 동일하며, 압력이 일정하거나 두 종 모두 같은 몰 질량을 가지고 있다고 가정합니다. 이러한 조건에서 Ref.^[7]는 기체의 운동 이론에서 이러한 Fick의 법칙 버전으로 확산 방정식이 어떻게 감소하는지 자세히 보여줍니다.

\mathbf {V_{i}} =-D\nabla \ln y_{i},

여기

서_i V는 종

i

의 확산 속도입니다. 종의 흐름으로 볼 때 이것은

\mathbf {J_{i}} =-{\frac {\rho D}{M_{i}}}\nablay_{i}

$추가적$ 으로 $\nabla \rho =0$ ∇ ρ = 0 {\ $displaystyle$ \n인 경우 $bla \rho$ $=$ $0$ 이것은 픽 법칙의 가장 일반적인 형태로 축소됩니다.

\mathbf {J_{i}} =-D\nbla \varphi .

(∇ ρ = 0 ${\displaystyle$ \n의 instead 또는 $\nabla \rho =0$ 추가)인 경우 $abla \rho$ $=$ $0$ 두 종 모두 같은 어금니 질량을 가지고 있으며, Fick의 법칙은

\mathbf {J_{i}} =-{\frac {\rho D}{M_{i}}}\n공백_{i}

x_{i}

서

x_{i}

{\

는

x_{i}

종

i

의 몰 분율입니다.

픽의 제2법칙

픽의 제2법칙은 확산이 어떻게 시간에 대한 농도의 변화를 일으키는지 예측합니다. 편미분 방정식으로 1차원에서 다음과 같이 표시됩니다.

{\frac {\partial \varphi}{\partial t}}=D\,{\frac {\partial ^{2}\varphi}{\partial x^{2}}

어디에

$φ$ 는 [ $[{\mathsf {N}}{\mathsf {L}}^{-3}]$ L - 3] ${\displaystyle [{\mathsf$ { $N}}{\mathsf {L$ 3}}의 $[{\mathsf {N}}{\mathsf {L}}^{-3}]$ 농도이며, $예$ 를 들어 mol/m이고, $φ$ $=$ $φ$ (x,t)는 위치 x와 시간 t에 $의존$ 하는 $함수$ 입니다.
$이번$ 에는, 예를 들어,
$D$ 는 $[{\mathsf {L}}^{2}{\mathsf {T}}^{-1}]$ [ $[{\mathsf {L}}^{2}{\mathsf {T}}^{-1}]$ $[{\mathsf {L}}^{2}{\mathsf {T}}^{-1}]$ $[{\mathsf {L}}^{2}{\mathsf {T}}^{-1}]$ - $[{\mathsf {L}}^{2}{\mathsf {T}}^{-1}]$ ${\displaystyle [{\mathsf {L}}^{2}{\mathsf {T}}^{-1$ 예 m/s²
$x$ 는 위치이고, 예제 m.

2차원 이상에서는 2차 도함수를 일반화하여 방정식을 얻는 라플라시안 δ∇ =를 사용해야 합니다.

{\frac {\partial \varphi}{\partial t}}=D\Delta \varphi

Fick의 제2법칙은 Heat 방정식과 같은 수학적 형태를 가지며, 확산 $계수$ D{\ $displaystyle$ D $}$ 로 $k$ $열전도율$ k $k$ 를 전환하는 것을 제외하고는 Heat 커널과 근본적인 해결책이 동일합니다 $D$

\varphi(x,t)={\frac {1}{\sqrt {4\pi Dt}}\exp \left (-{\frac {x^{2}}{4Dt}}\right)

픽 제2법칙의 유도

픽의 제2법칙은 픽의 제1법칙과 화학적 반응이 없는 질량 보존으로부터 유도될 수 있습니다.

{\frac {\partial \varphi }{\partial t}}+{\partial  x}}+{\partial x}}J=0\오른쪽 화살표 {\frac {\partial \varphi }{\partial t}}-{\frac {\partial  x}}-{\partial x}}-{\left(D{\frac {\partial  x}}{\partial x}}\varphi \right)\,=0

확산 계수 $D$ 를 상수라고 가정하면 미분의 차수를 교환하고 상수를 곱할 수 있습니다.

{\frac {\partial}{\partial x}}\left(D{\frac {\partial x}}\varphi \right)=D{\frac {\partial }{\partial x}}{\frac {\partial  x}}{\partial x}}\varphi =D{\frac {\partial ^{2}\varphi}{\partial x^{2}}

따라서 위에서 언급한 것과 같은 픽 방정식의 형태를 얻습니다.

2차원 이상의 확산의 경우 Fick의 제2법칙은

{\frac {\partial \varphi}{\partial t}}=D\,\nabla ^{2}\varphi ,

열 방정식과 유사합니다.

확산 계수가 상수가 아니라 좌표 또는 농도에 의존하는 경우, Fick의 제2법칙은 다음과 같습니다.

{\frac {\partial \varphi}{\partial t}}=\nabla \cdot (D\,\nbla \varphi )

$중요$ 한 예는 φ가 정상 상태에 있는 경우, 즉 시간에 따라 농도가 변하지 않으므로 위 식의 왼쪽 부분이 동일하게 0이 되는 경우입니다. 상수 $D$ 가 있는 1차원에서 농도에 대한 해는 $x$ 를 따라 농도가 선형으로 변하는 것입니다. 2개 이상의 차원에서 우리가 얻는

\nabla ^{2}\varphi =0,

수학자들이 조화 함수라고 부르는 라플라스 방정식입니다.

예제 솔루션 및 일반화

Fick의 제2법칙은 대류-확산 방정식의 특별한 경우로, 대류-확산 방정식에서 대류 플럭스가 없고 순 체적 소스가 없습니다. 연속 방정식에서 다음과 같이 유도할 수 있습니다.

{\frac {\partial \varphi}{\partial t}+\nabla \cdot \mathbf {j} =R,

여기서 $j$ 는 $총$ 플럭스이고 $R$ 은 φ에 대한 순 체적 소스입니다. 이 상황에서 유일한 플럭스 공급원은 확산 플럭스로 가정합니다.

\mathbf {j} _{\text{diffusion}}=-D\nabla \varphi

확산 플럭스의 정의를 연속 방정식에 연결하고 소스가 없다고 가정하면 ( $R$ = 0) Fick의 두 번째 법칙에 도달합니다.

{\frac {\partial \varphi}{\partial t}}=D{\frac {\partial ^{2}\varphi}{\partial x^{2}}

플럭스가 확산 플럭스와 확산 플럭스 모두의 결과라면 대류-확산 방정식이 그 결과입니다.

예제 용액 1: 일정한 농도원과 확산길이

$x$ = 0 $위치$ 에 위치한 경계에서 $시간$ t를 1차원(x축으로 taken)으로 확산하는 단순한 경우이며, 여기서 농도는 $n$ 으로 유지됩니다.

n\left(x,t\right)=n_{0}\operatorname {erfc} \left ({\frac {x}{2\sqrt {Dt}}\right)

여기서 $erfc$ 는 상보 오차 함수입니다. 이는 부식성 가스가 산화층을 통해 금속 표면을 향해 확산되는 경우(환경 내 가스 농도가 일정하고 확산 공간, 즉 부식 생성물 층이 반무한적이라고 가정할 경우)입니다. 차례로 확산 공간이 무한대인 $경우 (n (x,$ 0 $)$ = $0$ , $x$ > 0인 층과 n(x, 0) = n, x ≤ 0인 층 모두에서 지속됨), n 앞의 계수 1/2(현재 확산이 양방향으로 발생함에 따라)로 해가 수정됩니다. 이 경우는 $농도$ 가₀ n인 일부 용액을 순수 용매 층에 접촉시켰을 때 유효합니다(Bokstein, 2005). $길이$ 2 √Dt는 확산 길이라고 불리며, 시간 $t$ 에서 확산에 의해 농도가 x 방향으로 얼마나 멀리 전파되었는지 측정할 수 있습니다(Bird, 1976).

오차 함수의 빠른 근사값으로 테일러 급수의 처음 두 항을 사용할 수 있습니다.

n(x,t)=n_{0}\left[1-2\left ({\frac {x}{\sqrt {Dt\pi}}}\right)\right]

$D$ 가 시간 의존적이면 확산 길이는

2{\sqrt {\int _{0}^{t}D\tau \,d\tau }}.

이 아이디어는 $D$ 가 온도에 따라 변하는 가열 및 냉각 사이클에 대한 확산 길이를 추정하는 데 유용합니다.

예제 솔루션 2: 브라운 입자와 평균 제곱 변위

확산의 또 다른 단순한 경우는 한 입자의 브라운 운동입니다. 원래 위치에서 입자의 평균 제곱 변위는 다음과 같습니다.

{\text{MSD}}\equiv \langle (\mathbf {x} -\mathbf {x_{0}} )^{2}\rangle =2nDt

여기서

n

n

은

n

입자의 브라운 운동의 차원입니다. 예를 들어 8nm 두께의 세포막을 가로질러 분자가 확산되는 것은 구형대칭성 때문에 1-D 확산이지만, 분자가 막에서 진핵세포의 중심으로 확산되는 것은 3-D 확산입니다. 원통형 선인장의 경우 표면의 광합성 세포에서 중심으로 확산되는 것(원기둥 대칭축)은 2차원 확산입니다.

MSD의 제곱근인 ${\sqrt {2nDt}}$ ${\sqrt {2nDt}}$ ${\$ 은 $시간$ t $t$ 이 $t$ 경과한 후 입자가 얼마나 멀리 이동했는지에 대한 특성으로 자주 사용됩니다. MSD는 1D, 2D 및 3D 공간에 대칭적으로 분포됩니다. 따라서 1D에서 MSD 크기의 확률 분포는 가우시안이고 3D는 맥스웰-볼츠만 분포입니다.

일반화

비균질 매체에서는 확산 계수가 공간에 따라 $달라지는데$ , $D$ = D $(x$ )입니다. 이러한 의존성은 픽의 제1법칙에는 영향을 미치지 않지만 제2법칙은 바뀝니다. ${\frac {\partial \varphi(x,t)}{\partial t}}=\nabla \cdot {\bigl (}D(x)\nabla \varphi (x,t){\bigr )}=D(x)\델타 \varphi (x,t)+\sum _{i=1}^{3}{\frac {\partial D(x)}{\partial x_{i}}{\frac {\partial \varphi(x,t)}{\partial x_{i}}$
이방성 매질에서는 확산 계수가 방향에 따라 달라집니다. 대칭 텐서 D = D 입니다. 픽의 첫 번째 법칙은 다음과 같이 바뀝니다. $J=-D\nbla \varphi,$ 이것은 텐서와 벡터의 곱입니다. $J_{i}=-\sum _{j=1}^{3}D_{ij}{\frac {\partial \varphi }{\partial x_{j}}}.$ 확산 방정식의 경우, 이 공식은 다음과 같습니다. ${\frac {\partial \varphi(x,t)}{\partial t}}=\nabla \cdot {\bigl (}D\nabla \varphi (x,t){\bigr )}=\sum _{i=1}^{3}\sum _{j=1}^{3}D_{ij}{\frac {\partial ^{2}\varphi (x,t)}{\partial x_{i}\partial x_{j}}}.$ 확산 계수 $D$ 의_ij 대칭 행렬은 양의 정의 행렬이어야 합니다. 오른쪽 조작자를 타원형으로 만들기 위해 필요합니다.
비균질 이방성 매질의 경우 이 두 형태의 확산 방정식은 다음과 같이 결합되어야 합니다. ${\frac {\partial \varphi(x,t)}{\partial t}}=\nabla \cdot {\bigl (}D(x)\nabla \varphi (x,t){\bigr )}=\sum _{i,j=1}^{3}\left(D_{ij}(x){\frac {\partial ^{2}\varphi(x,t)}{\partial x_{i}\partial x_{j}}+{\frac {\partial D_{ij}(x)}{\partial x_{i}}}{\frac {\partial \varphi(x,t)}{\partial x_{i}}}\right.$
아인슈타인의 이동성과 테오렐 공식에 기초한 접근법은 완벽한 성분의 다성분 확산에 대한 픽 방정식의 다음과 같은 일반화를 제공합니다. ${\frac {\partial \varphi _{i}}{\partial t}}=\sum _{j}\nabla \cdot \left(D_{ij}{\frac {\varphi _{i}}{\varphi _{j}}}\nabla \,\varphi _{j}\right)$ $여기$ 서 φ은 $성분$ 의 농도이고 D는 계수의 행렬입니다. 여기서 인덱스 $i$ 와 $j$ 는 공간 좌표가 아니라 다양한 성분과 관련이 있습니다.

기체 내 확산에 대한 채프먼-엔스코그 공식은 정확히 같은 용어를 포함합니다. 이러한 확산의 물리적 모델은 균일 평형에서 매우 작은 편차에 유효한 테스트 모델∂φ = σ D δ φ과 다릅니다. 앞서 맥스웰-스테판 확산 방정식에 이와 같은 항이 도입된 바 있습니다.

비등방성 다성분 확산 계수의 경우 순위 4 텐서(예: D)가 $필요$ 합니다. $여기$ 서 i, $j$ 는 성분을 나타내고 $α,$ $β$ = $1,$ 2, $3$ 은 공간 좌표에 해당합니다.

적용들

Fick의 법칙에 기초한 방정식은 식품, 뉴런, 생체 고분자, 의약품, 다공성 토양, 개체군 역학, 핵 물질, 플라즈마 물리학 및 반도체 도핑 공정의 수송 공정을 모델링하는 데 일반적으로 사용되었습니다. 전압전류법의 이론은 픽 방정식의 해를 기반으로 합니다. 반면, "피키안(수송 방정식의 또 다른 일반적인 근사치는 확산 이론의 근사치)"^[8] 설명이 부적절한 경우도 있습니다. 예를 들어, 고분자 과학과 식품 과학에서는 유리 전이를 겪고 있는 물질의 성분 수송을 설명하기 위해 보다 일반적인 접근법이 필요합니다. 또 다른 일반적인 프레임워크는 다성분 물질 전달의 맥스웰-스테판 확산 방정식으로^[9], 혼합물이 매우 희석되고 모든 화학 종이 다른 종과는 상호 작용하지 않을 때 Fick의 법칙을 제한적인 경우로 얻을 수 있습니다. 희석되지 않은 혼합물에서 여러 종의 존재를 설명하기 위해 Maxwell-Stefan 방정식의 여러 변형이 사용됩니다. 비다각형 결합 전송 프로세스(Onsager 관계)도 참조하십시오.

Fick의 액체 흐름

혼합 가능한 두 액체가 접촉하여 확산이 일어날 때, 거시적(또는 평균적) 농도는 피크의 법칙에 따라 진화합니다. 메조스코픽 스케일, 즉 Fick's law에 의해 기술된 거시적 스케일과 분자적 스케일 사이에서 분자 랜덤 워크가 일어나는 곳에서는 변동을 무시할 수 없습니다. 이러한 상황은 란다우-리프시츠 변동 유체역학으로 성공적으로 모델링할 수 있습니다. 이 이론적 틀에서 확산은 분자 규모에서 거시 규모에 이르는 차원의 변동으로 인한 것입니다.^[10]

특히 변동 유체역학 방정식에는 변동을 설명하는 유체역학 방정식 및 확률적 용어와 함께 주어진 확산 계수를 가진 Fick의 흐름 항이 포함됩니다. 섭동적 접근법으로 요동을 계산할 때 0차 근사는 픽의 법칙입니다. 첫 번째 순서는 변동을 제공하고 변동이 확산에 기여한다는 것이 밝혀집니다. 낮은 차수의 근사로 설명되는 현상은 높은 근사의 결과이기 때문에 이 문제는 변동하는 유체역학 방정식을 다시 정규화함으로써만 해결됩니다.

묽은 용질의 흡착속도 및 충돌빈도

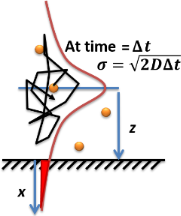
용액 내 분자 확산 방식. 주황색 점은 용질 분자이고, 용매 분자는 그려지지 않으며, 검은색 화살표는 예시적인 무작위 보행 궤적이며, 빨간색 곡선은 픽의 확산 법칙에서 확산 가우시안 확대 확률 함수입니다.^[11]^{:Fig. 9}

Fick의 확산 법칙을 이용하여 (기체 또는 액체) 용액 내의 표면 또는 계면에 대한 묽은 용질의 흡착 또는 흡수 속도를 계산할 수 있습니다. 표면에 흡착된 누적 분자 수는 시간에 따른 확산 플럭스 방정식을 적분하여 단시간 한계에서 Langmuir-Schaefer 방정식으로 표현됩니다.^[12]

\Gamma = 2AC{\sqrt {\frac {Dt}{\pi }}}

$\Gamma$ $γ$ ${\$ displaystyle \Gamma}는 $t$ displaystyle t} 시간 $동안$ 된 단위 # 분자의 개수입니다.
$A$ 는 표면적(m²)입니다.
$C$ 는 벌크 용액 내 흡착제 분자의 수 농도(#/m³)입니다.
흡착기의 확산계수( $m$ ²/s).
$경과$ 시간입니다.

이 방정식은 미국의 화학자 어빙 랭무어와 빈센트 셰퍼의 이름을 따서 지어졌습니다.

Langmuir-Schaefer 방정식은 표면에서 거부된 분자의 "역확산"을 설명하기 위해 Ward-Tordai 방정식으로 확장될 수 있습니다.^[13]

\Gamma = 2AC{\sqrt {\frac {Dt}{\pi }}}-A{\sqrt {\frac {D}{\pi }}}\int _{0}^{\sqrt {t}}{\frac {C_{\text{b}}(\tau )}{\sqrt {t-\tau }}}\,d\tau

여기서 $C$ {\ $displaystyle$ C $}$ 는 벌크 농도이고, $C_{\text{b}}$ {\ $displaystyle C_{\text{b}}$ 는 서브 표면 농도(흡착의 반응 모델에 따라 시간의 함수)이며 $,$ τ ${\displaystyle$ \tau}는 더미 변수입니다.

몬테카를로 시뮬레이션은 이 두 방정식이 표면 근처에서 예측 가능한 농도 구배를 형성하지만 일반적인 바이오 감지 시스템이나 흐름 및 대류가 중요한 경우와 같이 예측 불가능한 농도 구배가 없거나 있는 시스템에 문제가 있는 시스템의 흡착 속도를 예측하는 데 작동한다는 것을 보여줍니다.^[14]

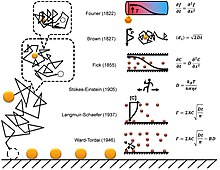
확산 흡착의 간단한 이력이 그림에 나와 있습니다.^[14] 단일 분자 수준에서 확산 흡착을 이해하는 눈에 띄는 과제는 확산의 프랙탈 특성입니다. 대부분의 컴퓨터 시뮬레이션은 각 단계 내에 자기 유사한 미세 확산 이벤트(프랙탈)가 있다는 사실을 무시하고 확산을 위한 시간 단계를 선택합니다. 프랙탈 확산 시뮬레이션은 고정된 시간 단계 흡착 시뮬레이션의 결과에 대해 두 가지 보정 계수를 도입하여 위의 두 방정식과 일치해야 함을 보여줍니다.^[14]

위 식들의 더 문제가 되는 결과는 이상적인 상황에서 흡착의 하한을 예측하지만 실제 흡착 속도를 예측하기는 매우 어렵다는 것입니다. 표면 근처에 안정적인 농도 구배가 형성되었을 때 장기간 한계 조건에서 방정식이 유도됩니다. 그러나 실제 흡착은 종종 이 무한한 시간 한계보다 훨씬 더 빠르게 이루어지는데, 즉, 하부 표면에서 농도의 농도 구배, 붕괴는 표면이 포화되기 전에 부분적으로만 형성됩니다. 따라서 측정된 흡착 속도는 낮은 에너지 장벽 흡착 또는 그렇지 않은 에너지 장벽 흡착에 대해 예측된 방정식보다 거의 항상 빠릅니다(예를 들어 흡수 속도를 크게 늦추는 중요한 흡착 에너지 장벽이 없는 경우). 물-공기 또는 물-substrate 계면에서 단층의 자가 조립 속도가 수천 배에서 수백만 배 더 빠릅니다. 이처럼 표면 근처에서 농도 구배의 진화를 계산하고, 실제 응용을 위해서는 상상된 무한 진화를 멈출 수 있는 적절한 시간을 찾는 것이 필요합니다. 언제 멈출지 예측하기는 어렵지만 가장 짧은 시간을 계산하는 것은 비교적 쉽지만, 기판 표면에서 가장 가까운 이웃이 농도 구배의 축적을 느끼는 임계 시간. 이는 흡수기 역학에 영향을 미치는 확산 이외의 다른 요인이 없는 이상적인 상황에서 흡착 속도의 상한을 산출합니다.^[14]

\langle r\rangle ={\frac {4}{\pi }}Ac_{b}^{4/3}D

$r ⟩ {\displaystyl$ \rangle}은 흡착 에너지 장벽이 없는 상황에서 가정한 흡착 속도(단위 #/s)입니다.
$A$ 는 $A$ "무한하고 평평한" 기판의 관심 표면의 면적입니다(m²).
$C_{b}$ ${\$ 는 $C_{b}$ 벌크 용액(#/m³)에서 흡수제 분자의 농도입니다.
$D$ ${\displaystyle$ D $}$ 는 용액 내 흡수기의 확산 상수(m²/s)입니다 $D$ .
이러한 단위의 치수 분석이 만족됩니다.

이 식은 모든 시스템의 초기 흡착 속도를 예측하는 데 사용할 수 있습니다. 결합 부위가 기재 표면의 매우 작은 부분에 불과하고 표면 근처의 농도 구배가 형성되지 않은 경우에 일반적인 바이오센싱 시스템의 정상 상태 흡착 속도를 예측하는 데 사용될 수 있습니다. 또한 서브 표면에서 농도 구배를 매우 얕게 밀기 위해 상당한 흐름이 있을 때 표면의 분자 흡착 속도를 예측하는 데 사용할 수 있습니다.

초단시간한계에서 확산시간 a²/D, 여기서 a는 입자반경, 확산은 랑게빈 방정식으로 기술됩니다. 더 긴 시간에서는 Langevin 방정식이 Stokes-Ainstein 방정식으로 합쳐집니다. 후자는 장거리 확산이 고려되는 희석 용액의 조건에 적합합니다. Langevin 방정식을 기반으로 한 변동-분산 정리에 따르면, 입자가 주변 유체보다 상당히 밀도가 높을 때 시간 의존적 확산 상수는 다음과 같습니다.^[15]

D(t)=\mu \,k_{\rm {B}}T\left(1-e^{-t/(m\mu )}\right)

여기서(SI 단위로 모두)

k는_B 볼츠만 상수입니다.
T는 절대온도 입니다.
μ는 유체 또는 기체 내 입자의 이동도이며, 아인슈타인 관계(동역학 이론)를 사용하여 계산할 수 있습니다.
m은 입자의 질량입니다.
시간입니다.

물의 유기 분자나 생체 분자(예: 단백질)와 같은 단일 분자의 경우 피코초 영역에서 mμ의 작은 생성물로 인해 지수항은 무시할 수 있습니다.

관심 영역이 분자의 크기(구체적으로, DNA와 같은 긴 원통형 분자)인 경우, 흡착 속도 방정식은 희석된 용액 내의 두 분자의 충돌 빈도를 나타내며, 한 분자는 특정한 면에 있고 다른 분자는 비스테릭 의존성, 즉 분자(무작위 배향)가 다른 면에 부딪히는 것. 확산 상수는 두 확산 분자 사이의 상대 확산 상수로 업데이트되어야 합니다. 이 추정은 특히 단백질과 같은 작은 분자와 더 큰 분자 사이의 상호작용을 연구하는 데 유용합니다. 유효 확산 상수는 확산 상수를 대신 사용할 수 있는 작은 것이 지배적입니다.

위의 적중률 방정식은 표면에서 분자 자기 조립의 동역학을 예측하는 데에도 유용합니다. 분자는 벌크 용액에서 무작위로 배향됩니다. 분자의 1/6이 표면 결합 부위에 대한 올바른 방향, 즉 x, y, z 3차원에서 z 방향의 1/2을 갖는다고 가정하면 관심 농도는 벌크 농도의 1/6에 불과합니다. 이 값을 식에 대입하면 Langmuir 흡착 모델을 이용하여 이론적인 흡착 운동 곡선을 계산할 수 있어야 합니다. 좀 더 엄격한 그림에서 1/6은 바인딩 지오메트리의 입체 인자로 대체될 수 있습니다.

단백질 응고/응집을 포함한 많은 반응과 관련된 이중 분자 충돌 빈도는 Brownian 운동과 Fick의 확산 법칙에서 파생된 ^[17]1916년 신간 간행물에서 Marian Smoluchowski가 제안한 Smoluchowski 응고 방정식에 의해 처음 기술되었습니다. 희석된 용액에서 A + B → 생성물에 대한 이상적인 반응 조건에서 Smoluchovski는 무한 시간 한계에서의 분자 플럭스가 표적 분자로부터 고정/stable 농도 구배를 산출하는 Fick의 확산 법칙으로부터 계산될 수 있다고 제안했습니다. 예를 들어, B는 상대적으로 고정된 상태를 유지하는 표적 분자입니다. 그리고 A는 A와 B 사이의 응고 반응으로 인해 표적 분자 B 근처에 농도 구배를 생성하는 이동 분자입니다. Smoluchowski는 단위 #/s/m을³ 사용하여 용액에서 A와 B 사이의 충돌 빈도를 계산했습니다.

Z_{AB}=4{\pi }RD_{r}C_{A}C_{B}

어디에,

$R$ ${\displaystyle$ R $}$ 은 $R$ (는) 충돌 반경입니다.
$D_{r}=D_{A}+D_{B}$ = $D_{r}=D_{A}+D_{B}$ + DB {\displaystyle D $D_{r}=D_{A}+D_{B}$ {r} = D_{A}+D_{B}}는 A와 B 사이의 상대 확산 상수(m/s)입니다.
$C_{A}$ ${\$ 와 $C_A$ $C_{B}$ ${\$ 는 각각 A와 B의 개수 농도(#/m³)입니다 $C_{B}$ .

이 2분자 반응의 반응 순서는 2로 분자의 이동 속도를 확산 플럭스로 대체하여 충돌 이론에서 나온 결과와 유사합니다. 충돌 이론에서 A와 B 사이의 이동 시간은 플럭스가 고정된 경우 확산 사례에 대해 유사한 관계인 거리에 비례합니다.

그러나 실제 조건에서 표적 분자 근처의 농도 구배는 시간이 지남에 따라 진화하고 있으며 분자 플럭스도 진화하고 ^[14]있으며 평균적으로 플럭스는 Smoluchowski가 제안한 무한 시간 제한 플럭스보다 훨씬 더 큽니다. 따라서 이 Smoluchowski 주파수는 실제 충돌 주파수의 하한을 나타냅니다.

2022년 첸은 움직이는 분자의 벌크 농도가 목표 분자의 가장 가까운 이웃 다음에 고정되어 있다고 가정하고 용액에서 A와 B의 충돌 주파수의 상한을 계산합니다.^[16] 따라서 실제 플럭스를 계산하기 위해 정지 시간이 주어진 가장 가까운 이웃 층에서 농도 구배 진화가 멈춥니다. 그는 이것을 임계 시간으로 명명하고 #/s/m³ 단위의 확산 충돌 빈도를 도출했습니다.^[16]

Z_{AB}={\frac {8}{\pi }}{\sigma }D_{r}C_{A}C_{B}{\sqrt[{3}]{C_{A}+C_{B}}

어디에,

$σ {\displaysty$ igma }}은 충돌 단면의 면적(m)입니다.
$D_{r}=D_{A}+D_{B}$ = $D_{r}=D_{A}+D_{B}$ + DB {\displaystyle D $D_{r}=D_{A}+D_{B}$ {r} = D_{A}+D_{B}}는 A와 B 사이의 상대 확산 상수(m/s)입니다.
$C_{A}$ ${\$ 와 $C_A$ $C_{B}$ ${\$ 는 각각 A와 B의 개수 농도(#/m³)입니다 $C_{B}$ .

이 방정식은 A와 B 사이의 확산 충돌 빈도의 상한을 첫 번째 이웃 층이 2가 아닌 2+1/3인 농도 구배의 진화를 느끼기 시작할 때로 가정합니다. Smoluchowski 방정식과 Jchen 방정식 모두 SI 단위로 치수 검사를 만족합니다. 그러나 전자는 반지름에 의존하고 후자는 충돌구의 면적에 의존합니다. 이분자 단위 반응의 실제 반응 순서는 2에서 2+1/3 사이일 수 있는데, 확산 충돌 시간은 두 분자 사이의 거리에 정방적으로 의존하기 때문에 타당합니다.

생물학적 관점

제1법칙은 다음과 같은 공식을 낳습니다.^[18]

{\text{flux}}={-P\left(c_{2}-c_{1}\right)}

에 있어서

$P$ 는 주어진 온도에서 주어진 기체에 대한 실험적으로 결정된 막 "전도도"인 투과도입니다.
$c 2$ - $c$ 는₁ 흐름 방향( $c$ 에서₁ $c$ 로₂)에 대한 멤브레인 전체의 가스 농도 차이입니다.

픽의 제1법칙은 방사선 전달 방정식에서도 중요합니다. 하지만 이런 맥락에서 확산 상수가 낮고 방사선이 흐르는 물질의 저항이 아니라 빛의 속도에 의해 방사선이 제한되면 부정확해집니다. 이러한 상황에서는 플럭스 리미터를 사용할 수 있습니다.

이 법칙과 그레이엄의 법칙을 함께 사용하면 유체막을 가로지르는 기체의 교환율을 알 수 있습니다.

확산이 제어될 때 희석된 용액의 조건하에서, 위 절에서 언급된 막 투과도는 마지막 절에서 언급된 식을 이용하여 용질에 대하여 이론적으로 계산될 수 있습니다(고밀도 용질에 대하여는 수식이 유도되므로 특히 주의하여 사용). 생물 분자가 물보다 밀도가 높지는 않지만):^[11]

P=2A_{p}\eta _{tm}{\sqrt {D/(\pi t)}}

어디에

$A_{P}$ ${\$ 는 $A_{P}$ 멤브레인(단위 m²)의 기공의 총 면적입니다.
$η$ tm {\displaystyle \eta _{tm}} 막횡단 효율(단위 없음), 크로마토그래피의 확률론으로 계산할 수 있습니다.
D는 용질 단위 m ⋅의 확산 상수입니다.
이것은 시간 단위입니다.
c₂, c₁ 농도는 단위 몰을⁻³ 사용해야 하므로 플럭스 단위는 몰이⁻¹ 됩니다.

플럭스는 이상적인 조건에서 시간이 지남에 따라 막 근처에 농도 구배가 쌓이기 때문에 시간의 제곱근에 걸쳐 붕괴됩니다. 흐름과 대류가 있을 때, 플럭스는 방정식이 예측하는 것과 크게 다를 수 있고 고정된 값으로 유효 시간 t를 나타낼 ^[14]수 있으므로 시간에 따른 붕괴 대신 플럭스가 안정적으로 됩니다. 구배가 형성되지 않은 이상적인 흐름 조건에서 임계 시간이 추정되었습니다.^[14]^[16] 이 전략은 혈액 순환과 같은 생물학에서 채택됩니다.

반도체 제조 애플리케이션

반도체는 일련의 장치를 통칭하는 용어입니다. 주로 2단자 장치, 3단자 장치, 4단자 장치의 세 가지 카테고리를 포함합니다. 반도체의 조합을 집적 회로라고 합니다.

피크의 법칙과 반도체의 관계 반도체의 원리는 화학물질이나 도펀트를 층에서 층으로 옮기는 것입니다. 픽의 법칙을 이용하면 수학을 통해 도펀트나 화학물질의 농도가 1미터당 1초에 얼마나 움직이는지 알 수 있어 확산을 제어하고 예측할 수 있습니다.

따라서 다양한 종류와 수준의 반도체를 제작할 수 있습니다.

집적회로 제조 기술, CVD, 열산화, 습식산화, 도핑 등의 모델 공정은 Fick의 법칙으로부터 얻어진 확산 방정식을 사용합니다.

반도체 제작 CVD법

웨이퍼는 실리콘 기판에 CVD 생성 폴리머 체인과 필름으로 코팅된 일종의 반도체입니다. 이 필름은 n형과 p형 도펀트를 함유하고 도펀트 전도를 담당합니다. CVD의 원리는 박막을 만들기 위해 기체상과 기체-고체 화학 반응에 의존합니다.

CVD의 점성 유동 방식은 압력 구배에 의해 구동됩니다. CVD에는 원자의 표면 확산과는 구별되는 확산 성분도 포함되어 있습니다. CVD에서는 반응물과 생성물이 기판 옆에 존재하는 정체된 가스의 경계층을 통해 확산되어야 합니다. CVD 막 성장에 필요한 총 단계 수는 경계층을 통한 반응물의 기상 확산, 원자의 흡착 및 표면 확산, 기판에서의 반응 및 경계층을 통한 생성물의 기상 확산입니다.

가스 흐름에 대한 속도 프로파일은 다음과 같습니다.

\delta(x)=\left ({\frac {5x}{\mathrm {Re} ^{1/2}}\right)\mathrm {Re} ={\frac {v\rho L}{\eta}

어디에

$δ$ {\ $displaysty$ lta }이(가) 두께입니다.
$\mathrm {Re}$ ${\$ 은 ${\mathrm {Re}}$ (는) 레이놀즈 숫자입니다.
$x$ 는 기판의 길이입니다.
$v$ $=$ $모든$ 표면에서 0
$η$ {\ $displaystyle$ \eta}은 $($ 는) 점도입니다.
$ρ$ {\ $displaystyle$ \rho}은 $($ 는) 밀도입니다.

$x$ 를 $0$ 에서 $L$ 까지 적분하면 평균 두께를 얻을 수 있습니다.

\delta ={\frac {10L}{3\mathrm {Re} ^{1/2}}

반응의 균형을 유지하려면 반응물이 정체된 경계층을 통해 확산되어 기질에 도달해야 합니다. 그래서 얇은 경계층이 바람직합니다. 방정식에 따르면 vo가 증가하면 더 많은 반응물이 낭비됩니다. 흐름이 난류가 되면 반응물이 균일하게 기판에 도달하지 못합니다. 또 다른 옵션은 점도나 밀도가 더 낮은 새로운 캐리어 가스로 전환하는 것입니다.

픽의 제1법칙은 경계층을 통한 확산을 설명합니다. 기체의 압력(P)과 온도(T)의 함수로서 확산이 결정됩니다.

D=D_{0}\left({\frac {P_{0}}{P}\right)\left({\frac {T}}{T_{0}}\right)^{3/2}

어디에

$P_{0}$ $P_{0}$ ${\$ 가 $P_{0}$ 표준 압력입니다.
$T_{0}$ $T_{0}$ ${\$ 는 $T_{0}$ 표준 온도입니다.
$D_{0}$ $D_{0}$ ${\$ 이 $D_{0}$ 표준 확산도입니다.

이 방정식은 온도를 높이거나 압력을 낮추면 확산율이 증가할 수 있음을 알려줍니다.

Fick의 제1법칙은 기질에 대한 반응물과 기질로부터 떨어진 생성물의 흐름을 예측합니다.

J=-D_{i}\left({\frac {dc_{i}}{dx}\right)

어디에

$x$ $x$ 은(는)두께 $\delta$ ${\displaysty$ $le \de$ lta }입니다.
$dc_{i}$ ${\$ 는 $dc_{i}$ 첫 번째 반응물의 농도입니다.

$PV=nRT$ 인 $PV=nRT$ $PV=nRT$ PV = $PV=nRT$ RT {\displaystyle PV = nRT}에서 가스의 농도는 부분 압력으로 표시됩니다.

J=-D_{i}\left({\frac {P_{i}-P_{0}}{\delta RT}}\right)

어디에

$R$ ${\displaystyle$ R $}$ 은 $R$ (는) 가스 상수입니다.
${\frac {P_{i}-P_{0}}{\delta }}$ - $δ {\$ displaystyle ${\frac {P_{$ i}-P_{ $0}}{\$ delta }}는 분압 구배입니다.

결과적으로 Fick의 제1법칙은 우리가 분압 구배를 사용하여 확산도를 조절하고 반도체 박막의 성장도 조절할 수 있음을 알려줍니다.

많은 현실적인 상황에서 단순한 픽의 법칙은 반도체 문제에 적합한 공식이 아닙니다. 반도체 경계 조건, 예를 들어, 일정한 소스 농도 확산, 제한된 소스 농도, 또는 이동 경계 확산(접합 깊이가 기판 내로 계속 이동하는)과 같은 특정 조건에만 적용됩니다.

피키안 확산의 무효화

초기에 반도체 제조(CVD 반응기 포함)에서 확산 프로세스를 모델링하는 데 피키안 확산이 사용되었지만, 종종 고급 반도체 노드(< 90 nm)에서 확산을 검증하지 못했다는 점에 유의할 필요가 있습니다. 이것은 대부분 피키안 확산이 분자 수준과 더 작은 크기에서 확산 과정을 정확하게 모델링할 수 없기 때문에 발생합니다. 첨단 반도체 제조에서는 연속체 확산에 의해 실패하는 원자 규모에서의 움직임을 이해하는 것이 중요합니다. 오늘날 대부분의 반도체 제조업체는 랜덤 워크를 사용하여 확산 과정을 연구하고 모델링합니다. 이를 통해 개별 원자, 분자, 플라즈마 등의 움직임을 이해하기 위해 확산의 영향을 이산적으로 연구할 수 있습니다.

이러한 과정에서 확산종(원자, 분자, 플라즈마 등)의 움직임은 CVD 반응기, 경계층, 재료 구조 등을 무작위로 통과한 후 이산 개체로 취급됩니다. 때로는 처리 조건에 따라 이동이 편향된 랜덤 워크를 따를 수도 있습니다. 통계 분석은 종의 무작위 보행으로 인해 발생하는 변동/위축성을 이해하기 위해 수행되며, 이는 결과적으로 전체 공정 및 전기적 변동에 영향을 미칩니다.

식품생산 및 조리

피크의 제1법칙의 공식화는 음식과 요리의 맥락에서 다양한 복잡한 현상을 설명할 수 있습니다. 에틸렌과 같은 분자의 확산은 식물의 성장과 숙성을 촉진하고, 소금과 설탕 분자는 고기의 소금물과 양념을 촉진하며, 물 분자는 탈수를 촉진합니다. 픽의 첫 번째 법칙은 또한 요리 중에 수분을 공급할 때 스파게티 면의 변화하는 수분 프로파일을 예측하는 데 사용될 수 있습니다. 이러한 현상은 모두 농도 구배에 의해 구동되는 용질 입자의 자발적인 움직임에 관한 것입니다. 다양한 상황에서 상수인 다른 확산성이 있습니다.^[19]

농도 구배를 조절하여 조리 시간, 음식의 모양, 염장 등을 조절할 수 있습니다.

참고 항목

인용

^
* Fick A (1855). "Ueber Diffusion". Annalen der Physik (in German). 94 (1): 59–86. Bibcode:1855AnP...170...59F. doi:10.1002/andp.18551700105.
- Fick A (1855). "On liquid diffusion". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 10 (63): 30–39. doi:10.1080/14786445508641925.
^ Philibert J (2005). "One and a Half Centuries of Diffusion: Fick, Einstein, before and beyond" (PDF). Diffusion Fundamentals. 2: 1.1–1.10. Archived from the original (PDF) on 5 February 2009.
^ Vázquez JL (2006). "The Porous Medium Equation". Mathematical Theory. Oxford Univ. Press.
^ Gorban AN, Sargsyan HP, Wahab HA (2011). "Quasichemical Models of Multicomponent Nonlinear Diffusion". Mathematical Modelling of Natural Phenomena. 6 (5): 184–262. arXiv:1012.2908. doi:10.1051/mmnp/20116509. S2CID 18961678.
^ Atkins P, de Paula J (2006). Physical Chemistry for the Life Science.
^ Conlisk AT (2013). Essentials of Micro- and Nanofluidics: With Applications to the Biological and Chemical Sciences. Cambridge University Press. p. 43. ISBN 9780521881685.
^ Williams FA (1985). "Appendix E". Combustion Theory. Benjamin/Cummings.
^ "Fickian Diffusion - an overview ScienceDirect Topics". www.sciencedirect.com. Retrieved 11 May 2022.
^ Taylor R, Krishna R (1993). Multicomponent mass transfer. Wiley Series in Chemical Engineering. Vol. 2. John Wiley & Sons. ISBN 978-0-471-57417-0.
^ Brogioli D, Vailati A (January 2001). "Diffusive mass transfer by nonequilibrium fluctuations: Fick's law revisited". Physical Review E. 63 (1 Pt 1): 012105. arXiv:cond-mat/0006163. Bibcode:2000PhRvE..63a2105B. doi:10.1103/PhysRevE.63.012105. PMID 11304296. S2CID 1302913.
^ ^a ^b Pyle JR, Chen J (2 November 2017). "Photobleaching of YOYO-1 in super-resolution single DNA fluorescence imaging". Beilstein Journal of Nanotechnology. 8: 2296–2306. doi:10.3762/bjnano.8.229. PMC 5687005. PMID 29181286.
^ ^a ^b Langmuir I, Schaefer VJ (1937). "The Effect of Dissolved Salts on Insoluble Monolayers". Journal of the American Chemical Society. 29 (11): 2400–2414. doi:10.1021/ja01290a091.
^ Ward AF, Tordai L (1946). "Time-dependence of Boundary Tensions of Solutions I. The Role of Diffusion in Time-effects". Journal of Chemical Physics. 14 (7): 453–461. Bibcode:1946JChPh..14..453W. doi:10.1063/1.1724167.
^ ^a ^b ^c ^d ^e ^f ^g ^h Chen J (January 2022). "Simulating stochastic adsorption of diluted solute molecules at interfaces". AIP Advances. 12 (1): 015318. Bibcode:2022AIPA...12a5318C. doi:10.1063/5.0064140. PMC 8758205. PMID 35070490.
^ Bian X, Kim C, Karniadakis GE (August 2016). "111 years of Brownian motion". Soft Matter. 12 (30): 6331–6346. Bibcode:2016SMat...12.6331B. doi:10.1039/c6sm01153e. PMC 5476231. PMID 27396746.
^ ^a ^b ^c ^d Chen J (December 2022). "Why Should the Reaction Order of a Bimolecular Reaction be 2.33 Instead of 2?". The Journal of Physical Chemistry A. 126 (51): 9719–9725. doi:10.1021/acs.jpca.2c07500. PMC 9805503. PMID 36520427.
^ Smoluchowski M (1916). "Drei Vorträge über Diffusion, Brownsche Molekularbewegung und Koagulation von Kolloidteilchen". Zeitschrift für Physik (in German). 17: 557–571, 585–599. Bibcode:1916ZPhy...17..557S.
^ Nosek TM. "Section 3/3ch9/s3ch9_2". Essentials of Human Physiology. Archived from the original on 24 March 2016.
^ Zhou L, Nyberg K, Rowat AC (September 2015). "Understanding diffusion theory and Fick's law through food and cooking". Advances in Physiology Education. 39 (3): 192–197. doi:10.1152/advan.00133.2014. PMID 26330037. S2CID 3921833.

외부 링크

픽 방정식, 볼츠만의 변형 등 (그림과 애니메이션 포함)
픽의 오픈스택스 제2법칙

[:0-1] * Fick A (1855). "Ueber Diffusion". Annalen der Physik (in German). 94 (1): 59–86. Bibcode:1855AnP...170...59F. doi:10.1002/andp.18551700105.
Fick A (1855). "On liquid diffusion". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 10 (63): 30–39. doi:10.1080/14786445508641925.

[2] Fick A (1855). "On liquid diffusion". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 10 (63): 30–39. doi:10.1080/14786445508641925.

[2] Philibert J (2005). "One and a Half Centuries of Diffusion: Fick, Einstein, before and beyond" (PDF). Diffusion Fundamentals. 2: 1.1–1.10. Archived from the original (PDF) on 5 February 2009.

[3] Vázquez JL (2006). "The Porous Medium Equation". Mathematical Theory. Oxford Univ. Press.

[GorbanMMNP2011-4] Gorban AN, Sargsyan HP, Wahab HA (2011). "Quasichemical Models of Multicomponent Nonlinear Diffusion". Mathematical Modelling of Natural Phenomena. 6 (5): 184–262. arXiv:1012.2908. doi:10.1051/mmnp/20116509. S2CID 18961678.

[5] Atkins P, de Paula J (2006). Physical Chemistry for the Life Science.

[6] Conlisk AT (2013). Essentials of Micro- and Nanofluidics: With Applications to the Biological and Chemical Sciences. Cambridge University Press. p. 43. ISBN 9780521881685.

[7] Williams FA (1985). "Appendix E". Combustion Theory. Benjamin/Cummings.

[8] "Fickian Diffusion - an overview ScienceDirect Topics". www.sciencedirect.com. Retrieved 11 May 2022.

[9] Taylor R, Krishna R (1993). Multicomponent mass transfer. Wiley Series in Chemical Engineering. Vol. 2. John Wiley & Sons. ISBN 978-0-471-57417-0.

[10] Brogioli D, Vailati A (January 2001). "Diffusive mass transfer by nonequilibrium fluctuations: Fick's law revisited". Physical Review E. 63 (1 Pt 1): 012105. arXiv:cond-mat/0006163. Bibcode:2000PhRvE..63a2105B. doi:10.1103/PhysRevE.63.012105. PMID 11304296. S2CID 1302913.

[Pyle-BJNano-11] Pyle JR, Chen J (2 November 2017). "Photobleaching of YOYO-1 in super-resolution single DNA fluorescence imaging". Beilstein Journal of Nanotechnology. 8: 2296–2306. doi:10.3762/bjnano.8.229. PMC 5687005. PMID 29181286.

[LangmuirSchaefer1937JACS-12] Langmuir I, Schaefer VJ (1937). "The Effect of Dissolved Salts on Insoluble Monolayers". Journal of the American Chemical Society. 29 (11): 2400–2414. doi:10.1021/ja01290a091.

[13] Ward AF, Tordai L (1946). "Time-dependence of Boundary Tensions of Solutions I. The Role of Diffusion in Time-effects". Journal of Chemical Physics. 14 (7): 453–461. Bibcode:1946JChPh..14..453W. doi:10.1063/1.1724167.

[JixinMCSimuAdsorption-14] ^ ^a ^b ^c ^d ^e ^f ^g ^h Chen J (January 2022). "Simulating stochastic adsorption of diluted solute molecules at interfaces". AIP Advances. 12 (1): 015318. Bibcode:2022AIPA...12a5318C. doi:10.1063/5.0064140. PMC 8758205. PMID 35070490.

[15] Bian X, Kim C, Karniadakis GE (August 2016). "111 years of Brownian motion". Soft Matter. 12 (30): 6331–6346. Bibcode:2016SMat...12.6331B. doi:10.1039/c6sm01153e. PMC 5476231. PMID 27396746.

[JChen2022JPCA-16] Chen J (December 2022). "Why Should the Reaction Order of a Bimolecular Reaction be 2.33 Instead of 2?". The Journal of Physical Chemistry A. 126 (51): 9719–9725. doi:10.1021/acs.jpca.2c07500. PMC 9805503. PMID 36520427.

[Smoluchowski1916-17] Smoluchowski M (1916). "Drei Vorträge über Diffusion, Brownsche Molekularbewegung und Koagulation von Kolloidteilchen". Zeitschrift für Physik (in German). 17: 557–571, 585–599. Bibcode:1916ZPhy...17..557S.

[18] Nosek TM. "Section 3/3ch9/s3ch9_2". Essentials of Human Physiology. Archived from the original on 24 March 2016.

[19] Zhou L, Nyberg K, Rowat AC (September 2015). "Understanding diffusion theory and Fick's law through food and cooking". Advances in Physiology Education. 39 (3): 192–197. doi:10.1152/advan.00133.2014. PMID 26330037. S2CID 3921833.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

Search