벌집 16셀

벌집 16셀
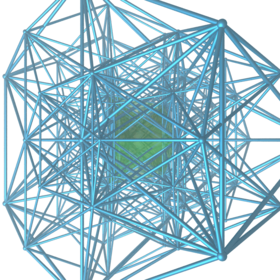투시 투영: 인접한 16-셀 면의 첫 번째 층.
유형	일반4벌집 제복4벌집
가족	교대형 하이퍼큐브 벌집
슐레플리 기호	{3,3,4,3}
콕시터 도표	= =
4면형	{3,3,4}
세포형	{3,3}
얼굴형	{3}
에지 피겨	정육면체
정점수	24셀
콕시터군	${\displaystyle {\stackrel{}{F}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$ = [3,3,4,3]
이중	{3,4,3,3}
특성.	정점 변환, 에지 변환, 얼굴 변환, 셀 변환, 4면 변환

4차원 유클리드 기하학에서 16셀 허니콤은 슐래플리 기호 {3,3,4,3}로 대표되는 3개의 정규 공간 채우기 테셀레이션(또는 허니콤) 중 하나이며, 모든 면에 3개의 16셀 팩스로 이루어진 4차원 패킹에 의해 건설되었다.

그것의 이중은 24셀 벌집이다.그것의 꼭지점은 24세포다.정점 배열을 B₄, D₄ 또는 F₄ 격자라고 한다.^[1][2]

대체 이름

• 육각체 테트라콤브/벌집합
• 단층 테트라콤/벌집합

좌표

정점은 모든 정수 좌표(i,j,k,l)에 배치하여 좌표의 합이 균등하도록 할 수 있다.

D₄ 격자

16셀 벌집모양의 꼭지점 배열을₄ D 격자 또는₄ F 격자라 한다.^[2]이 격자의 꼭지점은 4-공간에서 가장 밀도가 높은 것으로 알려진 포장에 있는 3-spres의 중심이다;^[3] 그것의 키스 번호는 또한 2003년에⁴ 올레그 무신이 증명했던 R의 키스 번호와 같은 24이다.^[4][5]

관련 D⁺
₄ 격자(D라고도²
₄ 함)는 두 개의₄ D 격자 조합으로 구성할 수 있으며,^[6] C 격자와₄ 동일하다.

∪ = =

D의⁺
₄ 키스 번호는 2³ = 8, (n < 8의 경우 2^{n – 1}, n = 8의 경우 240, n > 8의 경우 2n(n – 1)이다.^[7]

관련 D^*
₄ 격자(D와⁴
₄ C라고도²
₄ 함)는 4개의₄ D 격자 모두를 조합하여 구성할 수 있지만, D 격자와₄ 동일하다.또한 4차원 체형 중심 큐빅으로, 이중 포지션에 있는 두 개의 4-큐브 벌집합이 결합되어 있다.^[8]

∪ ∪ ∪ = = ∪ .

D^*
₄ 격자(및 D₄ 격자)의 키스 번호는 24이고^[9], 그것의 보로노이 테셀레이션은 24셀 벌집이며, 모든 수정 16셀(24셀) 보로노이 세포 또는 가 들어 있다.^[10]

대칭 구조

이 테셀레이션에는 세 가지 다른 대칭 구조가 있다.각 대칭은 색상의 16-셀 면의 다른 배열로 나타낼 수 있다.

콕시터군	슐레플리 기호	콕시터 다이어그램	정점수 대칭	면/Verf
${\displaystyle {\stackrel{}{F}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$ = [3,3,4,3]	{3,3,4,3}		[3,4,3], 1152번 주문	24:16 셀
${\displaystyle {\stackrel{}{B}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$ $$= [31,1,3,4]	= h{4,3,3,4}	=	[3,3,4] 주문 384	16+8: 16-셀
${\displaystyle {\stackrel{}{D}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$ $$= [31,1,1,1]	{3,31,1,1} = h{4,3,31,1}	=	[31,1,1], 주문 192	8+8+8: 16-셀
2×10 ${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$ = [[(4,3,3,3,4+,2)]]	ht0,4{4,3,4}			8+4+4: 4 데미큐브 8:16 셀

관련 허니컴

5정형 면의 일반 쌍곡 5공간 5정형 벌집, {3,3,3,4,3}, 정규 4폴리토프 24셀, 8정형(3정형) 셀의 경우 {3,4,3}, 정사각형 면의 큐브 {4,3}과 관련이 있다.

2차원 아날로그, {3,6}을(를) 가지며, 대체 형태(격리성 벌집, h{4,3,3,4})로 대체된 입방 벌집과 관련이 있다.

이 벌집합은 $D{\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 5_{\mathrm{}}}$ ${\$ Coxeter$$ 그룹에 의해 구성된 20개의 균일한 벌집합 중 하나이며, Coxeter-Dynkin 다이어그램의 고리의 그래프 대칭에서 볼 수 있는 확장 대칭에 의해 다른 패밀리에서 3개를 제외한 모든 것이 반복된다.20개의 순열은 대칭 관계가 가장 높은 것으로 나열된다.

D5 허니컴
확장됨 대칭	확장됨 도표를 만들다	확장됨 무리를 짓다	허니컴스
[31,1,3,31,1]		${\displaystyle {\tilde{D}_{5}}$
<[31,1,3,31,1]> ↔ [31,1,3,3,4]	↔	${\displaystyle {\stackrel{}{D}}_{}}$~ ${\displaystyle 5_{\mathrm{}}}$ ${\$ $\times$21 = $B{\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 5_{\mathrm{}}}$ ${\$	, , , , , ,
[[31,1,3,31,1]]		${\displaystyle {\stackrel{}{D}}_{}}$~ ${\displaystyle 5_{\mathrm{}}}$ ${\${5$}}$ $\times$22	,
<2[31,1,3,31,1]> ↔ [4,3,3,3,4]	↔	${\displaystyle {\stackrel{}{D}}_{}}$~ ${\displaystyle 5_{\mathrm{}}}$ ${\displaystyle {D}_{5}$ $\times$41 = ${\displaystyle C_{\mathrm{}}}$~ 5 ${\$	, , , , ,
[<2[31,1,3,31,1]>] ↔ [[4,3,3,3,4]]	↔	${\displaystyle {\stackrel{}{D}}_{}}$~ ${\displaystyle 5_{\mathrm{}}}$ ${\$ $\times$8 = $C{\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 5_{\mathrm{}}}$ ${\$ $\times$2	, ,

참고 항목

4-공간의 정규 및 균일한 벌집:

• 큐테라틱 벌집
• 24셀 벌집
• 잘린 24셀 벌집
• 스너브 24셀 벌집
• 5셀 벌집
• 잘린 5셀 벌집
• 잡동사니 5셀 벌집

메모들

참조

• Coxeter, H.S.M. 정규 폴리토페스 (3판, 1973년), 도버판, ISBN0-486-61480-8
  • 페이지 154–156: h 접두사로 표현되는 부분 절단 또는 교대: h{4,4} = {4,4}, h{4,3,4} = {3^1,1,3,4}, h{4,3,4} = {3,3,4,3}, ...
• 케일리디스코어: H.S.M. Coxeter의 선별된 글, F가 편집한 글.아서 셔크, 피터 맥멀런, 앤서니 C.Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN978-0-471-01003-6[1]
  • (용지 24) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 III, [산술]Zeit. 200 (1988) 3-45]
• 조지 올셰프스키, 균일 파노플로이드 테트라콤브스, 원고(2006) (11개의 볼록 균일 기울기, 28개의 볼록 균일 벌집, 143개의 볼록 균일 테트라콤 목록)
• Klitzing, Richard. "4D Euclidean tesselations". x3o3o4o3o - hext - O104
• Conway JH, Sloane NJH (1998). Sphere Packings, Lattices and Groups (3rd ed.). ISBN 0-387-98585-9.

v t 치수 2–9의 기본 볼록 정규 및 균일한 벌집
공간	가족	${\displaystyle {\tilde{A}_{n-1}$	${\displaystyle {\tilde{C}_{n-1}$	${\displaystyle {\tilde{B}_{n-1}$	${\displaystyle {\tilde{D}_{n-1}$	${\displaystyle {\stackrel{}{G}}_{}}$~ ${\displaystyle 2_{\mathrm{}}}$ ${\$G}$$${\displaystyle {\_}_{\mathrm{}}}$2}}$$/ F ~ 4 {\$displaystyle {\tilde{F}_{4}}$ $$/ $E{\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 1_{}}$ ${\$}
E2	균일 타일링	{3[3]}	δ3	Δ3	Δ3	육각형
E3	균일볼록 벌집	{3[4]}	δ4	Δ4	Δ4
E4	제복4벌집	{3[5]}	δ5	Δ5	Δ5	24셀 벌집
E5	제복5벌집	{3[6]}	δ6	Δ6	Δ6
E6	제복6벌집	{3[7]}	δ7	Δ7	Δ7	222
E7	제복7허니콤	{3[8]}	δ8	Δ8	Δ8	133 • 331
E8	제복8벌집	{3[9]}	δ9	Δ9	Δ9	152 • 251 • 521
E9	제복9벌집	{3[10]}	δ10	Δ10	Δ10
E10	제복10벌집	{3[11]}	δ11	Δ11	Δ11
En-1	제복(n-1)-벌집합	{3[n]}	δn	Δn	Δn	1k2 • 2k1 • k21