경계층
Boundary layer
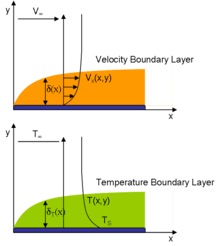
물리학과 유체역학에서 경계층(boundary layer)은 표면을 따라 흐르는 유체에 의해 형성되는 경계 표면 바로 근처에 있는 유체의 얇은 층이다.유체와 벽의 상호작용은 미끄럼 방지 경계 조건(벽에서 0 속도)을 유도한다.그러면 흐름 속도가 표면 위로 단조롭게 증가하여 벌크 흐름 속도로 돌아갑니다.속도가 아직 부피 흐름 속도로 돌아오지 않은 유체로 구성된 얇은 층을 속도 경계층이라고 합니다.
사람 옆의 공기는 가열되어 중력에 의해 유도되는 대류 기류, 즉 속도와 열 경계층을 모두 발생시킵니다.산들바람이 경계층을 파괴하고 머리카락과 옷이 경계층을 보호하여 사람을 더 시원하고 따뜻하게 만든다.항공기 날개에서 속도 경계층은 비점성 흐름이 주변의 비점성 흐름을 왜곡하는 날개 근처의 흐름 부분이다.지구 대기에서, 대기 경계층은 지면 근처의 공기층(~1km)이다.지표면의 영향을 받습니다.태양이 지면을 뜨겁게 달구거나 습기 또는 지표면에서 운동량이 전달되어 발생하는 주야간 열의 흐름입니다.
경계층의 종류
층계층은 그 구조 및 그 작성 상황에 따라 느슨하게 분류할 수 있다.진동하는 물체에 발달하는 얇은 전단층은 스토크스 경계층의 한 예이며, 블라시우스 경계층은 다가오는 단방향 흐름으로 유지되는 부착된 평판 및 블라시우스 프로파일의 일반화인 포크너-스칸 경계층 근처의 잘 알려진 유사성 솔루션을 참조한다.유체가 회전하고 (대류 관성이 아닌) 코리올리 효과에 의해 점성력이 균형을 이루면 에크만층이 형성됩니다.열전달이론에서는 열경계층이 발생한다.표면은 동시에 여러 종류의 경계층을 가질 수 있다.
공기 흐름의 점성이 표면에서 국소 속도를 감소시키고 피부 마찰을 일으킵니다.점도에 의해 느려지거나 멈추는 날개 표면 위의 공기층이 경계층이다.경계층 흐름에는 층류 및 [1]난류의 두 가지 유형이 있습니다.
층계층 흐름
난류 경계층은 소용돌이 또는 "에디"를 포함하는 반면, 층계 경계는 매우 부드러운 흐름입니다.층류는 난류보다 피부 마찰력이 덜하지만 안정성은 떨어집니다.날개면 상에서의 경계층 흐름은 매끄러운 층류로부터 시작된다.흐름이 선두에서 역류하면 층 경계층의 두께가 커집니다.
난류 경계층 흐름
전연에서 어느 정도 떨어진 곳에서 평탄한 층류가 분해되어 난류로 이행합니다.드래그 관점에서 볼 때 가능한 한 날개 뒤쪽에서 층류에서 난류로의 이행 또는 경계층의 층류 내에 날개면을 다량으로 하는 것이 바람직하다.그러나 낮은 에너지 층의 흐름은 난류층보다 더 갑작스럽게 분해되는 경향이 있습니다.
프란틀 경계층의 개념
공기역학적 경계층은 1904년 8월 12일 독일 하이델베르크에서 열린 제3차 국제 수학자 대회에서 발표된 논문에서 루드비히 프란틀에 의해 처음으로 저하상화 되었다.유동장을 2개의 영역으로 분할함으로써 유체 흐름의 방정식을 단순화합니다.하나는 점도에 의해 지배되고 경계체가 경험하는 대부분의 항력을 생성하는 영역과 다른 하나는 용액에 큰 영향을 주지 않고 점도를 무시할 수 있는 영역입니다.이를 통해 전체 Navier를 대폭 단순화함으로써 두 영역 모두에서 흐름의 클로즈드 폼 솔루션을 구현할 수 있습니다.-방정식을 스토크합니다.물과 같이 점도가 중간에서 낮은 다른 유체(공기 이외)에도 동일한 저체압이 적용됩니다.표면과 벌크유체 사이에 온도차가 있는 경우에는 물체와의 열전달의 대부분이 속도경계층 부근에서 일어나는 것을 알 수 있다.이렇게 하면 경계층 외부의 흐름 필드에서 방정식을 단순화할 수 있습니다.경계층 전체에 걸친 압력분포는 경계층 전체에 걸쳐 비교적 일정하게 유지되며(예: 에어포일) 표면과 동일하다.
속도 경계층의 두께는 일반적으로 고체에서 점성 흐름 속도가 자유 흐름 속도의 99%인 지점(무시력 [citation needed]흐름의 표면 속도)까지의 거리로 정의된다.변위두께는 벽면에 슬립이 있는 비점성 흐름에 비해 경계층이 질량 흐름의 부족을 나타낸다는 대체 정의입니다.비점성 케이스와 동일한 총 질량 흐름을 제공하기 위해 비점성 케이스에서 벽이 변위되어야 하는 거리입니다.미끄럼 방지 조건에서는 고체 물체 표면의 유속이 0이어야 하며 유체 온도는 표면 온도와 같아야 합니다.그러면 유속은 아래의 경계층 방정식에 의해 통제되는 경계층 내에서 빠르게 증가합니다.
열경계층의 두께는 온도가 프리스트림 온도의 99%인 물체로부터의 거리입니다.두 두께의 비율은 프란틀 숫자에 의해 제어됩니다.Prandtl 번호가 1이면 두 경계 레이어의 두께가 동일합니다.Prandtl 수가 1보다 크면 열경계층이 속도경계층보다 얇다.Prandtl 수치가 1 미만일 경우(표준 조건의 공기의 경우) 열경계층은 속도경계층보다 두껍다.
글라이더 및 상업용 항공기와 같은 고성능 설계에서는 항력을 최소화하기 위해 경계층의 거동을 제어하는 데 많은 주의를 기울인다.두 가지 효과를 고려해야 합니다.우선 경계층은 변위두께를 통해 본체의 유효두께를 가산하여 압력저항을 증가시킨다.둘째, 날개 표면의 전단력은 피부 마찰력을 발생시킨다.
일반 항공기의 전형적인 높은 레이놀즈 수치에서는 층 경계층을 갖는 것이 바람직하다.이로 인해 층류 특유의 속도 프로파일로 인해 피부 마찰이 감소합니다.그러나 경계층은 필연적으로 두꺼워지고 흐름이 본체를 따라 발달함에 따라 안정성이 떨어지며, 최종적으로 난류가 되는 과정, 즉 경계층 전이라고 불리는 과정이 된다.이 문제를 해결하는 한 가지 방법은 다공질 표면을 통해 경계층을 흡입하는 것입니다(경계층 흡입 참조).이렇게 하면 항력을 줄일 수 있지만 일반적으로 기계적 복잡성과 공기를 이동시키고 폐기하는 데 필요한 전력 때문에 실용적이지 않습니다.Natural Layer Flow(NLF; 자연층 흐름) 기술은 에어포일 또는 동체의 가장 두꺼운 점이 더 뒤쪽에서 덜 두껍게 되도록 재형성함으로써 경계층 천이를 후방으로 밀어냅니다.이렇게 하면 선두 부품의 속도가 감소하며 길이가 더 큰 동일한 레이놀즈 수가 달성됩니다.
모형 항공기에서 볼 수 있는 것과 같이 레이놀즈 수치가 낮을 경우 층류 유량을 비교적 쉽게 유지할 수 있다.이렇게 하면 피부 마찰이 적어지는 것이 바람직합니다.그러나 층 경계층에 낮은 피부 마찰을 주는 동일한 속도 프로필은 또한 역압 구배에 의해 악영향을 받습니다.압력이 날개 현의 뒷부분에서 회복되기 시작하면 층계층이 표면에서 분리되는 경향이 있습니다.이러한 흐름의 분리는 날개 부분의 유효 크기를 크게 증가시키기 때문에 압력 항력을 크게 증가시킨다.이 경우 난류기를 사용하여 층분리 위치 이전 지점에서 의도적으로 경계층을 난류로 트립하는 것이 유리할 수 있다.난류 경계층의 완전한 속도 프로파일은 분리 없이 역압 구배를 유지할 수 있게 한다.따라서 피부마찰은 증가하지만 전체적인 항력은 감소합니다.이는 골프공과 항공기의 소용돌이 발생기의 딤플링 원리다.또한 압력 회수를 맞춤형으로 하여 층 분리를 줄이거나 제거할 수 있도록 특수 날개 섹션도 설계되었습니다.이는 흐름 분리에 따른 압력 항력과 유도 난류로부터의 피부 마찰 사이의 최적의 균형을 나타냅니다.
풍동에 하프 모델을 사용할 때, 때때로 경계층의 영향을 줄이거나 제거하기 위해 페니체를 사용한다.
경계층 방정식
경계층 방정식의 추리는 유체 역학에서 가장 중요한 발전 중 하나였다.규모 분석을 사용하여 잘 알려진 통치자 Navier는–점성 유체 흐름의 스토크스 방정식은 경계층 내에서 크게 단순화할 수 있습니다.특히, 편미분방정식(PDE)의 특성은 풀 나비에의 타원형이 아니라 포물선이 된다.-방정식을 스토크합니다.이것은 방정식의 해법을 크게 단순화한다.경계층 근사를 함으로써 플로우를 비점성 부분(여러 가지 방법으로 해결이 용이한 부분)과 PDE가 용이한 경계층으로 분할한다.연속성과 Navier–데카르트 좌표의 2차원 안정 비압축 흐름에 대한 스토크스 방정식은 다음과 같다.
서u\u 및 \은 속도 성분, {\}는 p {\p}는 압력, {\ \nu은 유체의 한 지점에서의 운동학적 점도입니다.
근사치는 레이놀즈 수치가 충분히 높을 경우 표면을 통과하는 흐름이 점도의 영향을 받지 않는 비점성 흐름의 외부 영역(흐름의 대부분)과 점도가 중요한 표면에 가까운 영역(경계층)으로 나눌 수 있음을 나타냅니다. 내부에 각각 스트림 및 가로( 기준) 속도를 표시 및upsilon스케일 분석을 사용하여, 위의 운동 방정식이 경계층 내에서 감소하여 다음과 같이 된다는 것을 보여줄 수 있다.
액체가 압축할 수 없는 경우(액체가 표준 조건일 경우):
규모 분석 순서에서는 경계층 내부의 가로 길이 척도보다 훨씬 큰 스트림 길이 척도를 가정합니다.따라서 흐름 방향의 특성 변동은 일반적으로 벽 정상 방향의 특성 변동보다 훨씬 낮습니다.연속성 방정식에 적용하면 벽면 법선속도인 이 유속속도인u {\u}에 비해 작음을 알 수 있다.
정적 p p는y{ y와 독립적이기 때문에 경계층 가장자리에서의 압력은 주어진 스트림 위치에서 경계층 전체의 압력입니다.외부 압력은 베르누이 방정식의 적용을 통해 얻을 수 있다.U{\ U를 경계층 밖의 유체 속도라고 합니다. 서U {\U}와U {\ U는 둘 다 평행입니다.이것은p\p를 하면 다음과 같은 결과를 얻을 수 있습니다.
pp도 흐름의 방향으로 변화하지 않는 흐름의 경우
U\U는 일정하게 유지됩니다.
따라서, 운동 방정식은 단순화되어 다음과 같이 된다.
이러한 근사치는 과학 및 엔지니어링에 관심이 있는 다양한 실제 흐름 문제에 사용됩니다.위의 분석은 모든 순간 층 또는 난류 경계층에 대한 것이지만, 속도 변동이 없기 때문에 평균 흐름도 순간 흐름이기 때문에 주로 층류 연구에 사용된다.이 단순화된 방정식은 포물선 PDE이며 종종 Blasius 경계층이라고 불리는 유사성 솔루션을 사용하여 해결할 수 있습니다.
프란틀의 전위 정리
Frandtl은 경계층 방정식을 만족시키는 임의의 u,), vy, t u y, t , y, t v (( y, t) { u t}, v에서 검출했습니다.글쓰기에[2] 중독된.
서f () { f는 임의입니다.수학적 [3]관점에서 해답은 고유하지 않기 때문에 Stewartson과 Paul A가 나타내는[4] 것처럼 해답에 무한한 고유함수 집합 중 하나를 추가할 수 있습니다. 리비.[5][6]
폰 카르만 운동량 적분
폰 카르만은 1921년에 [7]경계층 방정식을 경계층 전체에 적분함으로써 적분 방정식을 도출했다.방정식은
어디에
- w w \{ w } 、 v w \ v { w } 1 \ \ _ { style 2 \ _ {} thickness thickness thickness thickness thickness thickness thickness thickness thickness thickness thickness thickness thickness thickness thickness thickness thickness thickness thickness thickness thickness thickness thickness thickness thickness thickness thickness thickness thickness thickness thickness thickness thickness thickness and thickness thickness thickness stress stress stress stress stress stress stress stress stress stress stress stress thickness stress stress stress stress stress카르만-폴하우젠 근사치는 이 방정식에서 도출된다.
에너지 적분
에너지 적분은 Vieghardt에 [8][9]의해 도출되었습니다.
어디에
- { displaystyle \ 은 경계층의 점도에 의한 소산률이며, 3 { \ \ display _ }}은 에너지 [10]두께입니다.
폰 미제 변환
꾸준한 2차원 경계 층 들어, 폰 Mises[11]는{\displaystyle \psi}(흐름 함수)){\displaystyle)}및 y{이\displaystyle}대신 독립 변수로와 U2− u2{\displaystyle \c를 종속 변수 χ을 사용한다){\displaystyle)}과 ψ하는 변환을 소개했다.안녕하세요)\u가 U그러면 경계층 방정식은
원래 변수는 다음 위치에서 복구됩니다.
이 변환은 나중에 폰 카르만과 HS [12]치엔에 의해 압축 가능한 경계층으로 확장된다.
크로코의 변형
꾸준한 2차원 압축할 수 있는 경계층은 루이지 Crocco[13]는{\displaystyle u}){\displaystyle)}및 y{이\displaystyle}대신 독립 변수로, 탭μ∂ u/∂는 y{\displaystyle \tau =\mu \p는 종속 변수 τ을 사용한다){\displaystyle)}, 그리고 당신은 데려가는 변환을 소개했다.artiuu가 /\y강세)를 선택합니다.그러면 경계층 방정식은
원래 좌표는 다음 위치에서 복구됩니다.
난류 경계층
난류 경계층의 처리는 흐름 속성의 시간 의존적인 변화 때문에 훨씬 더 어렵다.난류를 다루는 가장 널리 사용되는 기술 중 하나는 레이놀즈 분해를 적용하는 것이다.여기서 순간 흐름 특성은 변동 구성요소의 평균이 항상 0이라는 가정 하에 평균 및 변동 구성요소로 분해됩니다.이 기법을 경계층 방정식에 적용하면 문헌에서 자주 볼 수 없는 완전한 난류 경계층 방정식을 얻을 수 있습니다.
비슷한 order-of-magnitude 분석을 이용해서, 위의 방정식을 이끌기 위해 용어로 줄어들 수 있다.길이 규모 선택하면 그 streamwise-direction의 변경 내용을δ<>, <, 나는{\displaystyle \delta<><>;transverse-direction의 변화를 위해{\delta\displaystyle}및 L{L\displaystyle}δ.L}, x-momentum 방정식에:단순화된다.
이 공식은 벽에 있는 그no-slip 조건을 충족시켜 줄지 않는다.처럼 프란틀 그의 경계층 방정식에, 새로운, 작은 길이 규모의 운동량 방정식의 점성 용어가 되기 위해 선도적인 주문할 수 있도록 사용해야 한다.그 y-scale로η<><>δ{\displaystyle \eta<><>\delta}을 선택함으로써, 이"내부 경계층"의 주요 위해 운동량 방정식: 주어진다.
무한한 레이놀즈 수의 한계에서, 압력 구배 용어는 난류 경계층의 내부 지역에는 영향이 없는데 나타낼 수 있다.새"내부 스케일"η{\displaystyle \eta}은 끈적거리는 스케일, 그리고 주문ν 너 ∗{\displaystyle{\frac{\nu}{u_{*}의}은}}, 혼란스러운 변동을 이 사건은 마찰 속도에 너 ∗{\displaystyle u_{*}}이 속도 규모다.
층상 경계층 방정식과 달리, 다른 흐름 척도 세트(즉, 내부 및 외부 스케일링)에 의해 제어되는 두 개의 계통의 존재로 인해 난류 경계층에 대한 보편적인 유사성 솔루션을 찾는 것이 어렵고 논란이 되고 있다.흐름의 두 영역에 걸친 유사성 솔루션을 찾으려면 흐름의 두 영역에서 나온 솔루션을 점근적으로 일치시켜야 합니다.이러한 분석은 소위 로그 법칙 또는 멱함수 법칙을 산출합니다.
압축 가능한 [14][15]흐름의 에너지 방정식을 사용하여 열 경계층에도 위의 분석에 대한 유사한 접근방식이 적용되었습니다.
난류 경계층 방정식의 추가 u v ( { displaystyle { ' ' v ' )는 레이놀즈 전단 응력으로 알려져 있으며 선험적으로 알려져 있지 않습니다.따라서 난류 경계층 방정식의 해는 알려진 흐름 변수 또는 도함수 측면에서 레이놀즈 전단 응력을 표현하는 것을 목표로 하는 난류 모델을 사용해야 한다.이러한 모델의 정확성과 일반성의 결여는 현대 유체 역학에서 난류 특성을 성공적으로 예측하는 데 큰 장애물이다.
근벽 영역에는 일정한 응력층이 존재합니다.벽 근처의 수직 속도 변동의 감쇠로 인해 레이놀즈 응력 항이 무시될 수 있으며 선형 속도 프로파일이 존재한다는 것을 알 수 있습니다.이것은 매우 가까운 벽 영역에만 해당됩니다.
열 및 질량 전달
1928년 프랑스 엔지니어 앙드레 레베크는 흐르는 유체의 대류 열 전달이 [16][17]표면과 매우 가까운 속도 값에 의해서만 영향을 받는다는 것을 발견했습니다.큰 Prandtl 수의 흐름의 경우 표면에서 자유유동 온도로 온도/질량 전환이 표면과 가까운 매우 얇은 영역에 걸쳐 발생합니다.따라서, 가장 중요한 유체 속도는 속도 변화가 표면으로부터 정상 거리로 선형으로 간주될 수 있는 매우 얇은 영역 안에 있는 속도입니다.이렇게 해서
y { y \ 0인 경우
여기서 θ는 벽을 가로지르는 푸아세유 포물선의 접선이다.Lévéque의 솔루션은 Poiseuille 흐름으로의 열 전달에 특화되었지만, 그의 통찰력은 다른 과학자들을 열 경계층 [18]문제에 대한 정확한 해결책으로 이끌었습니다.Schuh는 경계층에서 u는 다시 y의 선형 함수이지만, 이 경우 벽 접선은 [19]x의 함수라고 관찰했다. 그는 이것을 Lévéque 프로파일의 수정된 버전으로 표현했다.
낮은 Pr 수치에서도 매우 근사한 결과를 얻을 수 Pr( 스타일 Pr이 1보다 훨씬 작은 액체 금속만 이러한 [18]방식으로 처리할 수 없습니다.1962년 Kestin과 Persen은 열경계층이 운동량층 내에 완전히 포함되어 있고 다양한 벽 온도 [20]분포에 대한 열전달 솔루션을 설명하는 논문을 발표했습니다.x 0 x에서 온도상승이 발생하는 평판의 문제에 대해서는 포물선 열경계층 방정식을 일반 미분방정식으로 환원하는 대체방법을 제안한다.이 방정식의 해인 유체 내 임의의 지점의 온도는 불완전한 감마 [17]함수로 표현될 수 있다.슐리칭은 열경계층 방정식을 완전하지 않은 감마 [21]함수가 동일한 일반 미분 방정식으로 감소시키는 등가 치환을 제안했다.
경계층 분석의 대류 전달 상수
Paul Richard Heinrich Blasius는 위의 층 경계층 [22]방정식에 대한 정확한 해답을 도출했다.경계층 의 두께는 레이놀즈 수(layer flow)
- { display \display } = 경계층의 두께 : v { \ infty}}의 99% 미만의 흐름 영역; { \ style x }는 반장판을 따라 하며 e { \ style Re는 vρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ by/μ { } ( { =} 밀도 및 { =} 동적 점도).
Blasius 솔루션은 차원 없는 형식의 경계 조건을 사용합니다.
- x - v - v x \ {_ { } - { S} = { v _ { \ - v _ { s } = { v _ { v _ { \ } { v _ 0 v _ 0 }
- x- S - S v \ - = { \ } 1} \ y \ 0 .
대부분의 경우 미끄럼 방지 경계 조건에서는 S(\S 플레이트 표면의 유체 속도가 모든 위치에서 플레이트 속도와 동일하다는 에 유의하십시오.플레이트가 움직이지 않으면 v 스타일 }=입니다. 오일 슬립이 [23]허용되면 훨씬 더 복잡한 유도가 필요합니다.
실제로 반무한판 상부의 경계층에서의 층속도 프로파일용 블라시우스 용액은 열전달을 위한 열전사와 질량전달을 위한 열전사와 농도전사 경계층을 기술하기 위해 쉽게 확장할 수 있다.이는 차동 x-모멘텀 밸런스(운동 등가)가 아니라 유사하게 도출된 에너지 및 질량 밸런스를 사용합니다.
에너지: v T x+ T y C 2 y \ style { \ T \ \ x} + } { \ T} = { \ r_ { }
질량: x c x + y A y A c ∂ \ {\ display \\ display x} + { \ \ \ \ A } \ \ d _ A }
운동량 밸런스는 운동학적 를 운동량 확산도로 볼 수 있다.에너지 밸런스에서는 이 값이 / C P \alpha = {k/\P로 대체되고 질량 밸런스에서는 도 B})로 대체됩니다.물질의 열확산률에서 k k는 열전도율,(\는 밀도, 는 열용량이다.첨자 AB는 A종이 B종으로 확산되는 확산성을 나타낸다.
B { =} = \라고 가정하면 이러한 방정식은 운동량 균형과 동등해집니다.따라서 Prandtl r / {{ Pr=\/\및 슈미트 S / A { Sc=\/}=1}에 대해서는 Blasius 솔루션이 직접 적용된다.
따라서이 도출은 관련된 형태의 경계조건을 displaystyle 를 T\ T c\displaystyle A종의 절대온도 또는 농도)로 한다.첨자 S는 표면 조건을 나타냅니다.
- { y } )
- { \ y = \ } 및 { \ x =}
유선 함수를 사용하여 Blasius는 플레이트 표면의 전단 응력에 대해 다음과 같은 해답을 얻었다.
그리고 경계 조건을 통해, 알려진 바로는
플레이트 표면에서 나오는 열/질량 플럭스에 대해 다음과 같은 관계를 제공합니다.
P r c { Pr ==}의
서 "T "는 흐름 영역입니다.서 T T 및 는 원거리 필드 [24]값의 99% 미만입니다.
독일 엔지니어 E는 특정 유체의 프란틀 수가 통일성이 아닌 경우가 많기 때문입니다.Ludwig Frandtl과 함께 일했던 Polhausen은 이러한 방정식을 경험적으로 확장하여 r1 (\ Pr1)에 적용하려고 시도했다. 그의 결과는 S (\ Sc[25]에도 적용될 수 있다.그는 Prandtl 수치가 0.6보다 클 경우 열 경계층 두께는 대략 다음과 같이 계산된다는 것을 알아냈다.
- P 1 / 3_ { = { 1 / 3 ) therefore therefore = S / 3 ( \_ { c } = { 1/ 3 } )
이 용액으로부터 경계층 흐름의 영역에 근거해 대류열/질량 전달 상수를 특성화할 수 있다.푸리에의 전도 법칙과 뉴턴의 냉각 법칙은 위에서 도출한 플럭스 항 및 경계층 두께와 결합됩니다.
그러면 반무한 평면상의 한 지점에서 국부 대류 x {\가 됩니다.플레이트 길이에 걸쳐 통합하면 평균값 제공
물질 전달 항( k = 대류 물질 전달 상수, A }) = B, / B Sc=\AB})에 대한 A종의 확산도 도출에 따라 다음과 같은 해결 방법을 얻을 수 있다.
이 용액은 프랜드틀/슈미트 수치가 0.[24]6보다 큰 층류에는 적용된다.
이 섹션은 확장해야 합니다.추가함으로써 도움이 될 수 있습니다. (2009년 4월) |
항공기에 적용되는 많은 원칙은 선박, 잠수함 및 해상 플랫폼에도 적용된다.
선박의 경우 항공기와 달리 수밀도의 변화가 무시할 수 있는 비압축성 흐름을 다룬다(1000kPa에 가까운 압력 상승은 2-3kg/m의3 변화만 초래한다).이 유체역학 분야는 유체역학이라고 불린다.선박 엔지니어는 먼저 유체역학을 설계하고 나중에 강도를 설계합니다.물의 높은 점도는 높은 전단응력을 생성하기 때문에 경계층의 발달, 파괴 및 분리가 중요해진다.
경계층 터빈
이 효과는 1913년 니콜라 테슬라에 의해 특허를 받은 테슬라 터빈에서 이용되었습니다.기존 터빈처럼 블레이드에 충돌하는 유체가 아니라 경계층 효과를 사용하기 때문에 블래드리스 터빈이라고 합니다.경계층 터빈은 응집형 터빈, 무공해 터빈 및 프란틀 층 터빈(루드비히 프란틀 이후)으로도 알려져 있습니다.
치수해석을 통한 실린더 내 과도경계층 두께 예측
원통형 흐름에 대한 과도력 및 점성력 방정식을 사용하여 Womersley 번호( w N_를 구하면 과도 경계층의 두께를 예측할 수 있습니다.
과도력 = w \
= 1 {{스타일 {v \
서로 동일하게 설정하면 다음과 같은 결과가 나옵니다.
델타에 대한 해결은 다음을 제공합니다.
무차원 형식:
서 w{ N _ { } = Womersley Number ; { \ \ = 밀도; { v = ; { \ } = 과도 경계 레이어의 ; { \ mu L} c 길이
치수해석을 통한 원통내 경계층의 대류상태 예측
원통형 흐름에 대한 경계층의 대류력 및 점성력 방정식을 사용하여 무차원 레이놀즈 수( e Re를 구함으로써 경계층의 대류 흐름 조건을 예측할 수 있습니다.
대류력: v L (\ v )
: † {\ v
서로 동일하게 설정하면 다음과 같은 결과가 나옵니다.
델타에 대한 해결은 다음을 제공합니다.
무차원 형식:
서 R e\ Re= 레이놀즈 수,; \ \= 밀도, \ v= 속도, 2 \ \ _ = 대류 경계층의 ,μ \ \ = 점도, \ L= 특성 길이.
경계층 섭취
경계층 섭취는 느린 동체 경계층을 흡입하고 웨이크에 다시 전원을 공급하여 항력을 줄이고 추진 효율을 개선하기 위해 항공기 연료 효율의 향상을 약속한다.기류가 일그러진 상태에서 작동하려면 팬이 무거워지고 효율이 떨어지기 때문에 통합이 어렵습니다.Aurora D8이나 프랑스 연구기관인 오네라의 노바 같은 개념에 사용되며, 동체 경계층의 [26]40%를 흡수하여 순항 시 5%를 절약합니다.
Airbus는 2018년 9월 ICAS 회의에서 Nautilius 개념을 제시했습니다. 모든 동체 경계층을 흡수하는 동시에 방위 흐름 왜곡을 최소화하기 위해 동체는 13-18:1 바이패스 비율 팬을 갖춘 두 개의 스핀들로 분할됩니다.추진 효율은 최대 90%까지 작고 가볍고 덜 복잡하고 소음이 적은 엔진으로 역회전 오픈 로터와 유사합니다.일반적인 언더윙 15:1 바이패스 비율 [26]엔진에 비해 연료 연소율을 10% 이상 낮출 수 있습니다.
「 」를 참조해 주세요.
- 경계층 분리
- 경계층 두께
- 열경계층 두께 및 형상
- 경계층 흡입
- 경계층 제어
- 경계 마이크
- 블라시우스 경계층
- 포크너-스칸 경계층
- 에크만층
- 행성 경계층
- 섭동 이론
- 벽의 로그 법칙
- 형상 계수(경계 도면층 흐름)
- 전단 응력
- 표면층
레퍼런스
- ^ Young, A.D. (1989). Boundary layers (1st publ. ed.). Washington, DC: American Institute of Aeronautics and Astronautics. ISBN 0930403576.
- ^ Prandtl, L. (1938). "Zur Berechnung der Grenzschichten". Zeitschrift für Angewandte Mathematik und Mechanik. 18 (1): 77–82. Bibcode:1938ZaMM...18...77P. doi:10.1002/zamm.19380180111.
- ^ 밴 다이크, 밀턴유체역학에서의 섭동법.포물선 프레스, 주식회사, 1975.
- ^ Stewartson, K. (1957). "On Asymptotic Expansions in the Theory of Boundary Layers". Journal of Mathematics and Physics. 36 (1–4): 173–191. doi:10.1002/sapm1957361173.
- ^ Libby, Paul A.; Fox, Herbert (1963). "Some perturbation solutions in laminar boundary-layer theory". Journal of Fluid Mechanics. 17 (3): 433. doi:10.1017/S0022112063001439. S2CID 123824364.
- ^ Fox, Herbert; Libby, Paul A. (1964). "Some perturbation solutions in laminar boundary layer theory Part 2. The energy equation". Journal of Fluid Mechanics. 19 (3): 433–451. Bibcode:1964JFM....19..433F. doi:10.1017/S0022112064000830. S2CID 120911442.
- ^ von Kármán, T. (1921). "Über laminare und turbulente Reibung". Zeitschrift für Angewandte Mathematik und Mechanik. 1 (4): 233–252. Bibcode:1921ZaMM....1..233K. doi:10.1002/zamm.19210010401.
- ^ 비그하트, K층계층의 계산을 위한 에너지 방정식.1946년 합동 정보 목표국
- ^ Wieghardt, K. (1948). "Über einen Energiesatz zur Berechnung laminarer Grenzschichten". Ingenieur-Archiv. 16 (3–4): 231–242. doi:10.1007/BF00548007. S2CID 119750449.
- ^ 로젠헤드, 루이스, ED층계층 경계층.클라렌든 프레스, 1963년
- ^ Tollmien, Walter; Schlichting, Hermann; Görtler, Henry; Riegels, F. W. (1961). "Bemerkungen zur Hydrodynamik". Ludwig Prandtl Gesammelte Abhandlungen. pp. 627–631. doi:10.1007/978-3-662-11836-8_49. ISBN 978-3-662-11837-5.
- ^ von Kármán, T.; Tsien, H. S. (1938). "Boundary Layer in Compressible Fluids". Journal of the Aeronautical Sciences. 5 (6): 227–232. doi:10.2514/8.591.
- ^ Crocco, L. "가스 중 경계층의 방정식의 특징적인 변환." ARC 4582(1939) : 1940.
- ^ von Karman, T. (1939). "The analogy between fluid friction and heat transfer". Transactions of the American Society of Mechanical Engineers. 61: 705–710.
- ^ Guo, J.; Yang, X. I. A.; Ihme, M. (March 2022). "Structure of the thermal boundary layer in turbulent channel flows at transcritical conditions". Journal of Fluid Mechanics. 934. Bibcode:2022JFM...934A..45G. doi:10.1017/jfm.2021.1157. ISSN 0022-1120. S2CID 246066677.
- ^ Lévêque, A. (1928). "Les lois de la transmission de chaleur par convection". Annales des Mines ou Recueil de Mémoires sur l'Exploitation des Mines et sur les Sciences et les Arts qui s'y Rattachent, Mémoires (in French). XIII (13): 201–239.
- ^ a b Niall McMahon. "André Lévêque p285, a review of his velocity profile approximation". Archived from the original on 2012-06-04.
- ^ a b Martin, H. (2002). "The generalized Lévêque equation and its practical use for the prediction of heat and mass transfer rates from pressure drop". Chemical Engineering Science. 57 (16): 3217–3223. doi:10.1016/S0009-2509(02)00194-X.
- ^ Schuh, H. (1953). "On Asymptotic Solutions for the Heat Transfer at Varying Wall Temperatures in a Laminar Boundary Layer with Hartree's Velocity Profiles". Journal of the Aeronautical Sciences. 20 (2): 146–147. doi:10.2514/8.2566.
- ^ Kestin, J. & Persen, L.N. (1962). "The transfer of heat across a turbulent boundary layer at very high prandtl numbers". International Journal of Heat and Mass Transfer. 5 (5): 355–371. doi:10.1016/0017-9310(62)90026-1.
- ^ Schlichting, H. (1979). Boundary-Layer Theory (7 ed.). New York (USA): McGraw-Hill.
- ^ Blasius, H. (1908). "Grenzschichten in Flüssigkeiten mit kleiner Reibung". Zeitschrift für Mathematik und Physik. 56: 1–37. (영어 번역)
- ^ Martin, Michael J. (2001). "Blasius boundary layer solution with slip flow conditions". AIP Conference Proceedings. Vol. 585. pp. 518–523. doi:10.1063/1.1407604. hdl:2027.42/87372.
- ^ a b Geankoplis, Christie J. 운송 프로세스 및 분리 프로세스 원칙: (단위 운영 포함)제4판어퍼 새들 리버, 뉴저지주: 프렌티스 홀 프로페셔널 테크니컬 레퍼런스, 2003.인쇄.
- ^ Pohlhausen, E. (1921). "Der Wärmeaustausch zwischen festen Körpern und Flüssigkeiten mit kleiner reibung und kleiner Wärmeleitung". Zeitschrift für Angewandte Mathematik und Mechanik. 1 (2): 115–121. Bibcode:1921ZaMM....1..115P. doi:10.1002/zamm.19210010205.
- ^ a b Graham Warwick (Nov 19, 2018). "The Week In Technology, November 19-23, 2018". Aviation Week & Space Technology.
- Chanson, H. (2009). Applied Hydrodynamics: An Introduction to Ideal and Real Fluid Flows. CRC Press, Taylor & Francis Group, Leiden, The Netherlands, 478 pages. ISBN 978-0-415-49271-3.
- A.D. Polyanin and V.F. Zaitsev, 비선형 편미분 방정식 핸드북, Chapman & Hall/CRC Press, Boca Raton – London, 2004.ISBN 1-58488-355-3
- A.D. 폴리아닌, A.M. 쿠테포프, A.V. 비야즈민 및 D.A. Kazenin, Hydroadynamics, Mass and Heat Transfer in Chemical Engineering, Taylor & Francis, London, 2002.ISBN 0-415-27237-8
- 헤르만 슐리칭, 클라우스 거스텐, E. 크라우스, H. 주니어 오어텔, C.Mayes '경계층 이론' 제8판 2004년판 스프링어 ISBN 3-540-66270-7
- John D. Anderson Jr., "Ludwig Frandtl의 경계층", Physical Today, 2005년 12월
- Anderson, John (1992). Fundamentals of Aerodynamics (2nd ed.). Toronto: S.S.CHAND. pp. 711–714. ISBN 0-07-001679-8.
- H. Tennekes and J. L. Lumley, "A First Course in Durblement", MIT Press, (1972)
- William K의 21세기 난기류 강연.조지
외부 링크
- 국립과학디지털도서관– 경계층
- Moore, Franklin K., "3차원 경계층의 변위 효과"NACA 보고서 1124, 1953.
- 벤슨, 톰 "경계층"NASA 글렌 러닝 테크놀로지입니다.
- 경계층 분리
- 경계층 방정식: 정확한 솔루션– EqWorld에서 제공
- Jones, T.V. 경계층 열전달
- "The revolutionary concept of "boundary layer" and its prevalence in aeronautics by Sourabh S. Diwan". YouTube. International Centre for Theoretical Sciences. February 18, 2022.







 속도 성분,
속도 성분, 

 유체의 한 지점에서의
유체의 한 지점에서의 






 검출했습니다.글쓰기에
검출했습니다.글쓰기에
 임의입니다.수학적
임의입니다.수학적 







 경계층의 점도에 의한
경계층의 점도에 의한 




![{\displaystyle {\begin{aligned}&\mu \rho u{\frac {\partial }{\partial x}}\left({\frac {1}{\tau }}\right)+{\frac {\partial ^{2}\tau }{\partial u^{2}}}-\mu {\frac {dp}{dx}}{\frac {\partial }{\partial u}}\left({\frac {1}{\tau }}\right)=0,\\[5pt]&{\text{if }}{\frac {dp}{dx}}=0,{\text{ then }}{\frac {\mu \rho }{\tau ^{2}}}{\frac {\partial \tau }{\partial x}}={\frac {1}{u}}{\frac {\partial ^{2}\tau }{\partial u^{2}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4fb1fe61083afecdabf54fe54eb101ba820a717)







![{\displaystyle u(y)=U\left[1-{\frac {(y-h)^{2}}{h^{2}}}\right]=U{\frac {y}{h}}\left[2-{\frac {y}{h}}\right]\;,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/823f8f75f57cfdb9b46572e46a4f5b04ebf97e00)



















 열전도율,
열전도율, 열용량이다.첨자 AB는 A종이 B종으로 확산되는 확산성을 나타낸다.
열용량이다.첨자 AB는 A종이 B종으로 확산되는 확산성을 나타낸다. 












 흐름 영역입니다.
흐름 영역입니다.
 적용될 수 있다.그는 Prandtl 수치가 0.6보다 클 경우 열
적용될 수 있다.그는 Prandtl 수치가 0.6보다 클 경우 열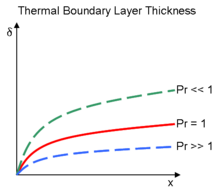




 됩니다.플레이트 길이에 걸쳐 통합하면 평균값 제공
됩니다.플레이트 길이에 걸쳐 통합하면 평균값 제공















