일치하는 점근확장법

수학에서, 일치된 점증적 팽창의 방법은 방정식, 즉 방정식의 시스템에 대한 정확한 근사치를 찾는 일반적인 접근법이다. 그것은 특히 특이하게 혼란스러운 미분 방정식을 풀 때 사용된다. 여기에는 각각 독립 변수의 범위에 대해 유효(즉, 정확)한 여러 가지 다른 근사 해법들을 찾아내고, 이러한 서로 다른 해법들을 함께 결합하여 독립 변수의 전체 값에 대해 유효한 단일 근사 해법들을 제공하는 것이 포함된다. 러시아 문헌에서는 이러한 방법들이 '중간증상증 약물'이라는 이름으로 알려져 야코프 젤도비치와 그리고리 바렌블라트의 작품에서 소개되었다.

방법 개요

특이하게 혼란에 빠진 문제의 큰 종류에서, 도메인은 둘 이상의 하위 영역으로 분할될 수 있다. 이들 중 하나에서, 종종 가장 큰 해결책은 문제를 규칙적인 섭동(즉, 비교적 작은 파라미터를 0으로 설정)으로 처리함으로써 발견되는 점증상 시리즈에^[1] 의해 정확히 근사하게 계산된다. 다른 하위 영역은 하나 이상의 작은 영역으로 구성되며, 일반적으로 문제의 섭동 용어들이 그곳에서 무시할 수 없기 때문에 근사치가 부정확하다. 이러한 영역은 전환 계층이라고 하며, 도메인 경계(응용프로그램의 일반적인 경우처럼)에서 발생하는지 또는 도메인 내부에서 발생하는지에 따라 경계 또는 내부 계층으로 불린다.

무증상 시리즈 형태의 근사치는 도메인의 그 부분을 별도의 섭동 문제로 처리함으로써 전환 계층에서 얻는다. 이러한 근사치를 "내부 솔루션"이라고 하며, 다른 하나는 전환 계층과의 관계를 위해 명명된 "외부 솔루션"이다. 그런 다음, 외부와 내부 솔루션은 전체 영역에 대한 대략적인 해결책이 얻어지는 방식으로 "매칭"이라고 불리는 과정을 통해 결합된다.^[2][3][4][5]

간단한 예

경계 값 문제 고려

${\displaystyle \varepsilon y'+(1+\varepsilon )y'+y=0,}$

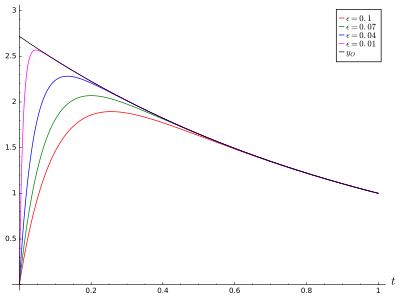
01을 주제로 독립적인 시간 변수 t{\displaystyle지}, 경계 조건은 y(0)=0{\displaystyle y(0)=0}과 y(1)=1{\displaystyle y(1)=1}의 어디 y{이\displaystyle}은 기능, 그리고 ε{\displaystyle \varepsilon}은 작은 매개 변수가 0<>ε ≪ 1{\dis.pla$ystyle$ 0$<\barpsilon \ll$ 1

외부 용액, t = O(1)에 유효

$\epsilon {\displaystyle }$ ${\displaystyle \varepsilon }$은(는) 매우$$ 작기 때문에, 우리의 첫 번째 접근법은 방정식을 규칙적인 섭동 문제로 취급하는 것이다. 즉, 근사치 $\epsilon {\displaystyle }$= $[\displaystyle \varepsilon =0}$을$($를)로 하고, 따라서 문제의 해결책을 찾는 것이다.

$y'+y=0.\,}$

또는 $y{\displaystyle }$ ${\displaystyle y}$과 t ${\displaystyle t}$이(가) 모두 O(1) 크기,$$ O(1$)({\$${\displaystyle }$ $\varepsilon }),$ O(1), O(1), O(\$displaystyle \varepsilon$ $\}),$ O(1)인 것을 고려하십시오. 따라서 이 시간 척도의 선도-주문 잔액은 ${\displaystyle \mathrm{고유}}$ 한계 →${\displaystyle }$→ 0 ${\displaystyle \varepsilon \to$ 0$\}$에서 유효하며, 두 번째와 네 번째 용어, 즉 $y{\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$+ ${\displaystyle \mathrm{y}}$= ${\displaystyle 0\mathrm{.}}$ ${\$에 의해 주어진다$.$$\,}$

이것은 해결책이 있다.

${\displaystyle y=Ae^{-t}\,}$

for some constant ${\displaystyle A}$. Applying the boundary condition ${\displaystyle y(0)=0}$, we would have ${\displaystyle A=0}$; applying the boundary condition ${\displaystyle y(1)=1}$, we would have ${\displaystyle A=e}$. It is therefore impossible to satisfy both boundary c따라서 ${\displaystyle \mathrm{\epsilon }}$= 0 ${\displaystyle \varepsilon =0}$은(는) 도메인 전체에 걸쳐 유효한 근사치가 아니다$$(즉, 이것은 단일 섭동 문제임). 이를 통해 우리는 $\epsilon {\displaystyle }$ ${\displaystyle \varepsilon }$이(가) 포함되어야$$ 하는 도메인의 끝점 중 하나에 경계층이 있어야 한다고 추론한다. 이 영역은 $독립{\displaystyle }$ 변수 $t{\displaystyle }$ ${\displaystyle$ t$\},$ $즉{\displaystyle }$ t ${\displaystyle t}$ 및$$$and{\displaystyle }$ {\$displaystyle \varepsilon }$에 비해 더 이상 무시할 수 없는$$ 영역이 될 것이다. 즉, 경계${\displaystyle \mathrm{층}}$이 $t{\displaystyle }$ =$$0 {\$displaystyt=0}$에 인접해 있다는$$ 것이다$.$ 따라서$$ 다른 ${\displaystyle \mathrm{경계}}$ 조건 y${\displaystyle }$(${\displaystyle }$1${\displaystyle }$) = ${\displaystyle 1}$ ${\displaystyle$y($1)=1$}이$($가) 이 외부 영역에$$ 적용되므로,${\displaystyle }A{\displaystyle }$ = e$${\$displaystyle A=e$ $즉{\displaystyle {}_{}}$ ${\displaystyle y_{}}$O = ${\displaystyle {}^{1\mathrm{}}}$ - ${\displaystyle t^{}{}^{}}${\$displaystyle y_{\mathrmethr {O}}$}=$e^{1-t}\}\}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$ 그것은 선도적인 해결책이다.

내부 용액, t = O(수평)에 유효

In the inner region, ${\displaystyle t}$ and ${\displaystyle \varepsilon }$ are both tiny, but of comparable size, so define the new O(1) time variable ${\displaystyle \tau =t/\varepsilon }$. Rescale the original boundary value problem by replacing ${\displaystyle t}$ with ${\displaystyle \tau \var$$엡실론 }$ $,$ 그리고 문제가 된다.

${\displaystyle {\frac {1}{\barepsilon }y"(\tau )+\left1+\varepsilon }\right){\frac {1}{\barepsilon }}{\varepsilon'}(\tau )=0,\,}$

$which{\displaystyle }$ ${\displaystyle \varepsilon }$을(를) 곱한 후$$ $\epsilon {\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle \varepsilon =0}$을$($를) 취하면 다음과 같다.

$'Y'+y'=0.\,}$

$또는{\displaystyle }$ t ${\displaystyle t}$이(${\displaystyle }$) 크기 O$({\displaystyle \varepsilon })$로 축소되었을$$ 때 $y{\displaystyle }$ ${\displaystyle y}$은(${\displaystyle {y\mathrm{}}_{}}$ O ${\$에 대한 표현 사용)$$ 크기가 여전히 O(1)이므로$$ 원래 방정식의 왼쪽에 있는 네 항이 각각 si임을 고려하십시오.zes O( ${\displaystyle }$ ${\displaystyle \varepsilon }),$ $$⁻¹O$([\displaystyle \varepsilon }$ }),$$⁻¹ O(1) 및 O(1). 따라서 이 시간 척도의 선도-주문 잔액은 구분 한계 ${\displaystyle \mathrm{\epsilon }}$→ 0 ${\displaystyle \varepsilon \to 0$에서 유효하며, 첫 번째와 두 번째 용어, 즉 $y{\displaystyle {}^{}}$ ${\displaystyle {″}^{}}$+ ${\displaystyle \mathrm{y}{}^{}}$=${\displaystyle }$0${\displaystyle \mathrm{.}}$ ${\$ y$'+y'=0$에 의해 주어진다$.$$\,}$

이것은 해결책이 있다.

${\displaystyle y=B-Ce^{-\tau }\,}$

일부 상수 $B{\displaystyle }$ ${\displaystyle$ $B$$}$ $및{\displaystyle }$ C$$ ${\displaystyle$ C$\}.$ $y{\displaystyle }$( 0${\displaystyle }$)${\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle y$ ($0)=0}$이(가) 이 내부 영역에 적용되기 $때문$에${\displaystyle }$B = ${\displaystyle C}${\$displaystyle$B=$C$이(가)를 제공하므로 이 내부 영역의 원래 경계 값 문제에 대한 정확한 대략적인 해결책(선

${\displaystyle y_{\mathrm {I}}=B\왼쪽({1-e^{-\tau }}\오른쪽)=B\왼쪽({1-e^{-t/\var렙실론 }}\오른쪽).\,}$

매칭

상수 $B{\displaystyle }$ ${\displaystyle B}$의 값을 찾기 위해 일치를 사용한다$.$ 일치의 발상은 중간(또는 겹침) 영역의 $t{\displaystyle }$ ${\displaystyle t}$ 값에 대해$$ 내측과 외측 솔루션이 일치해야 한다는 것이다$.$ 즉, $\epsilon {\displaystyle }$ ${\displaystyle \ll }$ ${\displaystyle \mathrm{t}}$ 1 ${\displaystyle \varepsilon \ll$ t$\ll 1$.외측 용액의 내측 한계와 일치하도록 내측 용액의 외측 한계가 필요하다. 즉, ${\displaystyle \underset{}{im}}$ ${\displaystyle \underset{}{\tau }}$→ ∞ ∞ ∞${\displaystyle \underset{}{\mathrm{}}}$∞ ∞ ∞ ${\displaystyle \underset{}{}{}_{}}$ y y y y y y ${\displaystyle {y\mathrm{}}_{}}$ y.${\displaystyle {}_{}=}$ ${\displaystyle \underset{}{lim}}$ ${\displaystyle \underset{}{t}}$→ ${\displaystyle \underset{}{0}}$ ${\displaystyle \underset{}{}{}_{}}$ ${\displaystyle O_{}}$, ${\${$O$$}}}}}}}\,},},},},}$을(이)로 B${\displaystyle }$= ${\displaystyle e}$ ${\displaystaystaysty$

위의 문제는 일치하는 점증적 팽창에 대처하는 간단한 문제들 중 가장 간단하다. One can immediately calculate that ${\displaystyle e^{1-t}}$ is the entire asymptotic series for the outer region whereas the ${\displaystyle {\mathcal {O}}(\epsilon )}$ correction to the inner solution ${\displaystyle y_{\mathrm {I} }}$ is ${\displays$$Tyle B_{1$}($1-e^{-t}-{\underline{et}})$ 및 통합$$ $B{\displaystyle {}_{}}$ ${\$1}의 상수는 내부 외측 일치를 통해 얻어야 한다$$.

주의할$$ 점은 한계치(${\displaystyle \underset{}{rem}}$ ${\displaystyle \underset{}{\tau }}$ →${\displaystyle \underset{}{\mathrm{\infty }}}$ ${\displaystyle {y\mathrm{}}_{}}$ ${\displaystyle \underset{}{}{}_{}}$= ${\displaystyle \underset{}{lim}}$ ${\displaystyle \underset{}{t}}$→ ${\displaystyle \underset{}{0}}$ y ${\displaystyle {o,}_{}}$ $\$\t$\t\to}y_{O}}}}}}}}}}},},},}}}}},}}}},}},},}}}}}}}}}}}}}}}}}}}}},$ 이것은 단순히 밑줄 친 용어가 한계에 수렴되지 않기 때문이다. 이러한 유형의 사례에서 따르는 방법은 중간 변수의 a) 방법을 택하거나 b) Van-Dyke 일치 규칙을 이용하는 것이다. 이전의 방법은 번거롭고 항상 효과가 있는 반면 반-다이크 일치 규칙은 구현이 쉽지만 적용 가능성은 제한적이다. 모든 필수 성분을 갖는 구체적인 경계 가치 문제는 다음과 같다.

경계 값 문제 고려

${\displaystyle \varepsilon y'-x^{2}y'-y=1,\cHB y(0)=y(1)=1}$

기존의 외부 확장 $y{\displaystyle {}_{}}$ ${\displaystyle O_{}}$= ${\displaystyle {y\mathrm{}}_{}}$ 0${\displaystyle {}_{}}$+ ${\displaystyle {\epsilon \mathrm{}}_{}}$ y ${\displaystyle {}_{}}$+${\displaystyle }$.${\displaystyle }$.${\displaystyle }$, ${\displaystyle y_{\mathrm {O}}}=y_{0}+\bar렙실론 y_{1}+,}$는 다음과$$ 같다.

${\displaystyle y_{}}$ ${\displaystyle {0\mathrm{}}_{}}$= ${\displaystyle \alpha }$ ${\displaystyle {}^{}}$ ${\displaystyle {1\mathrm{}}^{}}$/ x${\displaystyle {}^{}}$- ${\displaystyle 1}$ ${\displaystyle y_{0}=\displaystyle e^{1/x}-1$ 여기서 $\alpha {\displaystyle }$ ${\displaystyle \alpha$}은$($는) 일치를 통해 얻어야 한다$$.

그 문제는 왼쪽과 오른쪽 양쪽에 경계층이 있다. $0{\displaystyle \mathrm{}}$ ${\displaystyle 0}$ ${\displaystyle {근처}^{}}$에 있는 왼쪽 경계층의 두께는 ${\displaystyle {\epsilon \mathrm{}}^{}}$ 1${\displaystyle {}^{}}$/ 2 ${\$}}인$$ 반면$$, $1{\displaystyle \mathrm{}}$ ${\displaystyle \varepsilon$ $\}\}\{$$1$$/$2}}. $우선{\displaystyle }$ X${\displaystyle }$= ${\displaystyle x}$ /${\displaystyle {\epsilon \mathrm{}}^{}}$ 1${\displaystyle {}^{}}$/ 왼쪽 경계층의 솔루션을 계산해 보자.${\displaystyle X=x/\varepsilon ^{1/2},\;$$Y=y$ 그러면 왼쪽에서 만족하는 미분 방정식은

${\displaystyle Y'-\varepsilon ^{1/2}X^{2}Y'-Y=1,\quad Y(0)=1}$

따라서 확장 Y ${\displaystyle l^{}}$= ${\displaystyle {}_{}^{}}$ ${\displaystyle {0\mathrm{}}_{}^{}}$ ${\displaystyle {}_{}^{}}$+ ${\displaystyle {\epsilon \mathrm{}}^{}}$ 1${\displaystyle {}^{}}$/ ${\displaystyle {2\mathrm{}}^{}}$ Y ${\displaystyle {1\mathrm{}}_{}^{}}$/${\displaystyle }$2 ${\displaystyle {}_{}^{}}$ +${\displaystyle }$. , ${\displaystyle Y^{l}=$라고 가정한다.$Y_{0}^{l$}^{l$}+\varepsilon ^{1/2}Y_{1/2}^{l}+...,}$.

왼쪽에 있는 $O{\displaystyle \mathcal{}}$(${\displaystyle 1}$ $){\displaystyle${\$mathcal{O}(1$) 비균형$$ 상태는 $O{\displaystyle \mathcal{}}$( $){\displaystyle {\mathcal{O}(1)$에서 확장을 시작할 이유를 제공한다$.$ 선도주문 솔루션은 $Y{\displaystyle {}_{}^{}}$ 0 ${\displaystyle {}_{}^{}}$= ${\displaystyle 2}$ ${\displaystyle e^{}}$- ${\displaystyle {}^{}}$- ${\displaystyle 1}$ ${\displaystyle Y_{0}^{l}=2e^{-X}-1$입니다$.$

1${\displaystyle \mathrm{}}$- ${\displaystyle 1}$ ${\displaystyle 1-1}$의 van-Dyke$$ 일치로 ${\displaystyle \mathrm{\alpha }}$= 0$[\displaystyle \alpha =0}$을(를) 제공한다$.$

이제 오른쪽 재할인 $X{\displaystyle }$= (${\displaystyle 1}$- ${\displaystyle x}$)${\displaystyle }$/ ${\displaystyle \epsilon }$, ${\displaystyle Y}$= ${\displaystyle y}$ ${\displaystyle X=(1-x)/\bar렙실론 ,\;$에 대한 솔루션을 계산해 봅시다.$Y=y$ 그러면 오른쪽에서 만족하는 미분 방정식은

${\displaystyle Y'+(1-2\barepsilon$$Y'-\barepsilon Y=\varepsilon ,\quad$ Y$(1)=1$

그리고 그에 따라, 우리는 확장을 가정한다.

${\displaystyle$$Y_{0}^{r}^{r}+\varepsilon ^{1/2}Y_{1/2}^{r}+...$$}$.

오른쪽에 있는 $O{\displaystyle \mathcal{}}$(${\displaystyle 1}$ $){\displaystyle${\$mathcal{O}(1$) 비균형$$ 상태는 $O{\displaystyle \mathcal{}}$( $){\displaystyle {\mathcal{O}(1)$에서 확장을 시작할 이유를 제공한다$.$ The leading order solution is ${\displaystyle Y_{0}^{r}=(1-B)+Be^{-X}}$. This with ${\displaystyle 1-1}$ van-Dyke matching gives ${\displaystyle B=2}$. Proceeding in a similar fashion if we calculate the higher order-corrections we get the solutions as

${\displaystyle Y^{l}=2e^{-X}-1+\varepsilon ^{1/2}e^{-X}({\frac {X^{3}}{3}}+{\frac {X^{2}}{2}}+{\frac {X}{2}})+{\mathcal {O}}(\varepsilon )...,\quad X={\frac {x}{\varepsilon ^{1/2}}}}$.

${\displaystyle y}$ ${\displaystyle \equiv }$- ${\displaystyle 1}$ ${\displaystyle y\equiv -1$

${\displaystyle Y^{r}=2e^{-X}-1+2\varepsilon e^{-X}(X+X^{2})+{\mathcal {O}}(\varepsilon ^{2})...,\quad X={\frac {1-x}{\varepsilon }}}$.

복합용액

전체 도메인에서 유효한 최종 일치 복합 솔루션을 얻기 위해, 하나의 일반적인 방법은 통일된 방법이다. 이 방법에서는 내측 및 외측 근사치를 추가하고 겹치는 ${\displaystyle 값}$인 ${\displaystyle {\mathrm{y}}_{}}$ ${\displaystyle {\mathrm{o}}_{}}$ ${\displaystyle {\mathrm{e}}_{}}$ l ${\displaystyle {\mathrm{p}}_{}}$ ${\$을 뺀다. 중복되는 값은 내부 경계층 용액의 외부 한계와 외부 용액의 내부 한계로, 이러한 한계는 $e{\displaystyle }$ ${\displaystyle e$과 동일한 것으로 확인되었다. 따라서 이 경계 값 문제에 대한 최종 근사 해법은 다음과 같다.

${\displaystyle y(t)=y_{\mathrm {I} }+y_{\mathrm {O} }-y_{\mathrm {overlap} }=e\left({1-e^{-t/\varepsilon }}\right)+e^{1-t}-e=e\left({e^{-t}-e^{-t/\varepsilon }}\right).\,}$

$t$ ${\displaystyle t$$\}$이($)$ O$({\displaystyle$ $y_{\mathrm{I}}}}}$ 및$$ Y O ${\$$mathrm$${O}}}}}}}}}}$에 대한 ${\displaystyle {식}_{}}$으로 이 식이 올바르게 줄어든다는 점에 유의하십시오.

정확도

이 최종 해결책은 문제의 원래 미분방정식을 만족시킨다(그와 그 파생상품을 원래의 방정식으로 대체함으로써 나타난다). 또한 이 최종 해결책에 의해 생성된 경계 조건은 문제에 주어진 값과 일치하며, 일정한 배수까지 일치한다. 이는 용액의 고유성으로 인해 일치하는 무증상 용액이 상수 배수까지의 정확한 용액과 동일하다는 것을 의미한다. 반드시 그렇지는 않으며, 나머지 모든 용어는 $\epsilon {\displaystyle }$→ ${\displaystyle 0}$ $[\displaystyle \varepsilon \rightarrow 0}$으로 균일하게 0으로 되어야 한다$.$

우리의 해결책은 당면한 문제를 거의 성공적으로 해결할 뿐만 아니라, 문제의 정확한 해결책에 근접해 있다. 우연히 이 특정한 문제가 정확한 해결책을 가지고 있다는 것을 쉽게 발견할 수 있다.

${\displaystyle y(t)={\frac {e^{-t}-e^{-t/\varepsilon }}{e^{-1}-e^{-1/\varepsilon }}},}$

대략적인 용액과 동일한 형태를 가지며, 곱하기 상수를 사용한다. 대략적인 용액은 e ${\displaystyle {1\mathrm{}}^{}}$- ${\displaystyle 1^{}}$ /${\displaystyle {\epsilon }^{}}$ ${\$의 힘으로 정확한 용액을 이항적으로 확장한 첫 번째 용어다$.$

경계층 위치

편리하게도 $y{\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$ ${\$과 $y{\displaystyle {}^{}}$ ${\displaystyle {″}^{}}$ ${\$ y$'}$이(가) 큰$$ 경계층이 앞에서 생각했던 것처럼 $t{\displaystyle }$= ${\displaystyle 0}$ ${\displaystyt t=0$에 가깝다는 것을 알 수 있다. 만약 우리가 다른 엔드포인트에 있을 것으로 예상되었고, 재스케일링 $\tau {\displaystyle }$=${\displaystyle }$( 1${\displaystyle }$- ${\displaystyle t}$)${\displaystyle }$/ ${\displaystyle \tau$ = $(1-t)/\varepsilon }$을(를) 만드는 것으로 진행되었다면$,$ 우리는 결과적인 일치 조건을 만족시키는 것이 불가능하다는 것을 발견했을 것이다. 많은 문제에 있어서, 이러한 종류의 시행착오만이 경계층의 실제 위치를 결정할 수 있는 유일한 방법이다.^[2]

더 어려운 문제

위의 문제는 하나의 종속 변수만을 갖는 단일 방정식이고, 용액에는 하나의 경계층이 있기 때문에 간단한 예다. 더 어려운 문제는 여러 방정식의 시스템에 여러 개의 공동의존 변수를 포함하거나 해결책의 여러 경계 및/또는 내부 층을 포함할 수 있다.

종종 외부 용액과 내부 용액 모두의 점증적 팽창에서 더 많은 용어를 찾는 것이 바람직하다. 이러한 확장의 적절한 형태가 항상 명확한 것은 아니다: $\epsilon {\displaystyle }$ ${\displaystyle \var렙실론}$의 파워 시리즈 확장이 효과가 있을 수 있지만$$, 때때로 적절한 형태는 $\epsilon {\displaystyle }$ ${\displaystyle \mathrm{로그}}$ ${\displaystyle }$ ${\displaystyle \epsilon }$ $\$ {\$displaystyle \varepsilon$$}, et$ cetera와 같은 함수인$$$\$ {\\\displaystylevelopsilon $\valpart$ of power power power power power power power powers}의 파워를 포함한다. 위의 예에서와 같이 일치에 의해 결정되어야 하는 일부 계수를 가진 외부 및 내부 확장을 얻는다.^[6]

2차 미분 방정식

슈뢰딩거 유사 2차 미분 방정식

딩글과 뮐러-커스틴은 주기적인 슈뢰딩거식 2차 차동방정식의 점증적 확대와 특성수(밴드 경계)의 도출에 있어, 유효성의 공통 영역에서 해결책의 매칭과 일치하는 점증적 팽창의 방법을 개발하여 광범위하게 사용하였다. 전위 - 특히 마티외 방정식^[7](최상의 예), 라메 및 타원파 방정식,^[8] 지우기^[9] 및 탈구성^[10] 전위 방정식, 그리고 조화 전위를 갖는 방정식의 경우.^[11]

대류-확산 방정식

스몰루코프스키 대류-디퓨전 방정식의 대략적인 해결책을 찾기 위해 점증하지 않는 팽창 방법이 개발되었는데, 이것은 특이하게 동요된 2차 미분 방정식이다. 이 문제는 특히 선형 유동장의 콜로이드 입자의 맥락에서 연구되었는데, 여기서 변수는 시험 입자 주위의 쌍 분포 함수에 의해 주어진다. 낮은 Péclet 수의 한계에서는 대류-확산 방정식도 무한 거리(일반적으로 원거리 경계 조건이 배치되어야 하는 곳)에서 특이점을 나타내며, 이는 인터피사 분리에 있어서 흐름장이 선형이기 때문이다. 이 문제는 Jan Dhont가 보여주는 공간적 푸리에 변환으로 우회할 수 있다.^[12] 이 문제를 해결하기 위한 다른 접근방식은 알레시오 자코네와 동료들에 의해 개발되었으며, (1차 근사치에서) 대류가 지배적이기 때문에 외부 층에서 쌍 분포 함수의 상수 값을 가정할 때 경계 조건을 경계 층 거리에 바로 배치하는 것으로 구성된다. 이는 선형 유동장 내에서 상호작용하는 두 콜로이드 입자의 접촉률에 대한 대략적인 이론으로 이어지며, 완전한 수치 해법과 잘 일치한다.^[13] Péclet 번호가 1보다 유의하게 크면, 무한 분리에서의 특이점은 더 이상 발생하지 않으며, 일치된 점근법 방법을 적용하여 전체 도메인에서 쌍분포함수에 대한 풀 솔루션을 구축할 수 있다.^[14][15]

참고 항목

• 점근해석
• 다중 척도 분석
• 활성화 에너지 점증약물

참조