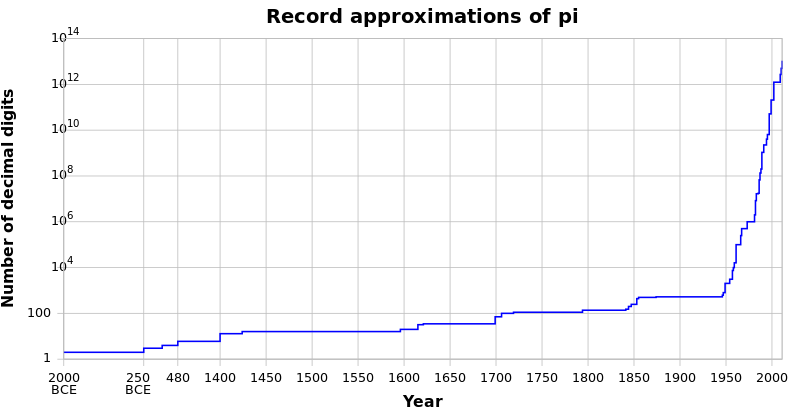
π의 연산 연대기

Chronology of computation of π
에 관한 일련의 기사의 일부
수학 상수 π
3.1415926535897932384626433...
사용하다
특성.
가치
사람
역사
문화에서
관련 항목

아래 표는 수학적 상수 pi(수학 상수 pi)의 계산된 숫자 값 또는 범위를 간략히 기록한 것이다. 이러한 계산 중 일부에 대한 자세한 설명은 π의 근사치를 참조하십시오.

최신 2021년 세계 기록 계산의 마지막 소수 자릿수는 다음과 같다.[1] 

6845711163 0056651643 5011939273 3317931338 5175251446  :  62,831,853,071,750 0666164596 1766612754 8681024493 0164977817 924264
소수 자릿수(로그 눈금에서 제외)로 측정한 pi에 대한 수치 근사치의 기록 정밀도가 인류 역사에서 어떻게 발전했는지 보여주는 그래프. 1400년 이전의 시간은 압축된다.

1400년 이전

날짜 누구 설명/계산 방법 사용 가치 소수점
(세계 기록)
굵은 글씨로)
2000년? 기원전 15년 고대 이집트인[2] 4 × (8⁄9)2 3.1605... 1
2000년? 기원전 15년 고대 바빌로니아인[2] 3 + 1⁄8 3.125 1
1200년? 기원전 15년 고대 중국어[2] 3 0
기원전 800-600년 샤타파타 브라흐마나 (산스크리트어:शतपथ ब्राह्मण) – 7.1.1.18 [3] 장방형 벽돌로 원형 제단을 만드는 방법에 대한 지침:

그는 (순환 부지를) 동쪽을 향해 달리는 네 개(브릭)를 쓰고, 두 개는 뒤쪽으로 (남쪽에서 북쪽으로) 달리고, 두 개는 앞쪽에 놓는다. 그가 동쪽으로 달려가는 네 개는 몸이다. 이 네 개는 몸통이다. 왜냐하면 이 몸이 네 부분으로 이루어져 있기 때문이다. 뒤에 있는 두 사람은 허벅지, 앞에 있는 두 사람은 팔뚝이다. 그리고 몸이 그 머리인 곳이기도 하다.[4]

(Sanskrit: "स चतस्रः प्राचीरुपदधाति द्वे पश्चात्तिरश्च्यौ द्वे पुरस्तात्तद्याश्चतस्रः प्राचीरुपदधाति स आत्मा तद्यत्ताश्चतस्रो भवन्ति चतुर्विधो ह्ययमात्माथ ये पश्चात्ते सक्थ्यौ ये पुरस्तात्तौ बाहू यत्र वा आत्मा तदेव शिरः)

(Sanskrit transliteration: sa catasraḥ prācīrupadadhāti dve paścāttiraścyau dve purastāttadyāścatasraḥ prācīrupadadhāti sa ātmā tadyattāścatasro bhavanti caturvidho hyayamātmātha ye paścātte sakthyau ye purastāttau bāhū yatra vā ātmā tadeva śiraḥ)

25⁄8 = 3.125 1
800년? 기원전 15세기경 술바수트라스[5]

[6][7]

(6⁄(2 + √2))2 3.088311 ... 0
550? 기원전 550년 성경(1왕 7:23)[2] "... 녹은 바다, 한쪽 테두리에서 다른 쪽 테두리까지 열 자루. 사방이 둥글고... 서른 자루로 된 줄이 나침반을 돌았다." 3 0
기원전 434년 아낙사고라스는 원을[8] 정사각형으로 만들려고 시도했다. 나침반과 직선자 아낙사고라스는 어떤 해결책도 제시하지 않았다. 0
기원전 250년 아르키메데스[2] 223⁄71 < π < 22⁄7 3.140845... < π < 3.142857... 2
기원전 15년 비트루비우스[6] 25⁄8 3.125 1
1시에서 5시 사이에 유신[6][9][10] π π ≈ 162⁄(√50+0.095) 값을 의미하는 지알리앙에 대한 수치를 제공하는 알 수 없는 방법.2 3.1547... 1
130 장행([2]후한) √10 = 3.162277...
736⁄232 		3.1622... 1
150 프톨레마이오스[2] 377⁄120 3.141666... 3
250 왕판[2] 142⁄45 3.155555... 1
263 유희[2] 3.141024 < π < 3.142074
3927⁄1250 		3.1416 3
400 허청톈[6] 111035⁄35329 3.142885... 2
480 주총지[2] 3.1415926 < π < 3.1415927
3.1415926 7
499 아리아바타[2] 62832⁄20000 3.1416 4[11]
640 브라마굽타[2] √10 3.162277... 1
800 알크화리즈미[2] 3.1416 4[11]
1150 바르스카라 2세[6] 3927⁄1250 및 754⁄240 3.1416 4[11]
1220 피보나치[2] 3.141818 3
1320 자오유우킨[6] 3.141592 6

1400–1949

날짜 누구 참고 소수점
( 굵게 표시된 세계 기록)
1400년 이후의 모든 기록은 정확한 소수 자릿수로 주어진다.
1400 마드하바 π의 무한 파워 시리즈 확장을 발견했고,
지금은[12] 파이용 라이프니즈 공식으로 알려져 있다. 		10
1424 잠쉬드 알카슈[13] 16
1573 발렌티누스 오토 355⁄113 6
1579 프랑수아 비에트[14] 9
1593 아드리아 반 라멘[15] 15
1596 루돌프 판 쿨렌 20
1615 32
1621 윌레브레퍼드 스넬 (스넬리우스) 반 쿨렌의 제자 35
1630 크리스토프 그리엔베르거[16][17] 38
1654 크리스티안 후이겐스 Richardson 외삽에 상당하는 기하학적 방법을 사용 10
1665 아이작 뉴턴[2] 16
1681 세키 다카카즈[18] 11
16
1699 에이브러햄 샤프[2] 72자리까지 계산된 pi가 모두 정확한 것은 아님 71
1706 존 마친[2] 100
1706 윌리엄 존스 그리스 문자 'π'를 소개했다.
1719 토마스 판타지 데 라그니[2] 127개의 소수 자릿수를 계산했지만 모두 정확하지는 않았다. 112
1722 가마타 도시키요 24
1722 다케베 가타히로 41
1739 마쓰나가 요시스케 51
1748 레온하르트 오일러 Analysisin Infinitorum의 그의 책 Introductio에서 그리스 문자 'π'을 사용하고 그 인기를 확신했다.
1761 요한 하인리히 램버트 π이 비이성적이라는 것을 증명했다.
1775 오일러 π이 초월적일 가능성을 지적했다.
1789 주리베가 소수점 143자리 계산되었지만 모두 정확한 것은 아님 126
1794 주리베가[2] 소수점 140자리 계산되었지만 모두 정확한 것은 아님 136
1794 아드리아-마리 레전드르 π2(그리고 따라서 π)은 비이성적이라는 것을 보여주고, π이 초월적일 가능성을 언급했다.
18세기 후반 익명 원고 F. X. von Zach에 의해 발견된 영국 옥스포드의 Radcliffe 도서관에서 나타나 154자리의 pi 값을 제공하며, 그 중 152자리는 정확했다. 152
1824 윌리엄 러더퍼드[2] 소수점 208자리 계산했지만 모두 정확하지는 않았다. 152
1844 자카리아스 다세 스트라스니츠키[2] 소수점 205자리 계산되었지만 모두 정확한 것은 아님 200
1847 토머스 클로스엔[2] 계산된 250개의 소수 자릿수, 그러나 모두 정확한 것은 아니다. 248
1853 레만[2] 261
1853 러더퍼드[2] 440
1874 윌리엄 샨크스[2] 소수점 707자리 계산에 15년이 걸렸지만 모두 정확하지는 않았다(D에 의해 오류가 발견되었다). F. 퍼거슨 (1946년) 527
1882 페르디난트 폰 린데만 π이 초월적(Lindemann-)임을 증명했다.위어스트라스 정리)
1897 미국 인디애나 주 π에 대한 가치 3.2(다른 것 중)를 입법화 할 뻔했다. 하원 법안 246호는 만장일치로 통과되었다. 이 법안은 교과서의 출판과 관련된 상업적 동기의 가능성으로 인해 주 상원에서 제동이 걸렸다.[19] 1
1910 라마누잔 스리니바사 π의 각 항에 대해 π의 소수점 8자리를 계산할 수 있는 π의 몇 개의 급속하게 수렴되는 무한 시리즈를 발견했다. 1980년대 이후 그의 시리즈는 현재 가나다 야스마사, 추드노브스키 형제가 π을 계산하기 위해 사용하고 있는 가장 빠른 알고리즘의 기초가 되었다.
1946 D. F. 퍼거슨 지금까지 손으로 계산한 숫자 중 가장 많은 숫자. 620
1947 이반 니븐 π이 비이성적이라는 아주 기초적인 증거를 주었다.
1947년 1월 D. F. 퍼거슨 탁상용 계산기 사용 710
1947년 9월 D. F. 퍼거슨 탁상계산기 808
1949 Levi B. Smith and John Wrench 탁상용 계산기 사용 1,120

1949–2009

날짜 누구 실행 시간 소수점
( 굵게 표시된 세계 기록)
1949년 이후의 모든 기록은 전자 컴퓨터로 계산되었다.
1949 G. W. Reitwiesner 외 전자 컴퓨터(ENIAC)를 사용하여 π을 계산하는 첫 번째 방법 70시간 2,037
1953 쿠르트 말러 π은 Louville 번호가 아니라는 것을 보여주었다.
1954 S. C. 니콜슨 & J. 지넬 NORC[21] 사용 13분 3,093
1957 조지 E. 펠턴 Ferranti Pegasus 컴퓨터(런던)는 10,021개의 숫자를 계산했지만 모두 정확한[22] 것은 아니었다. 7,480
1958년 1월 프랑수아 지누이스 IBM 704[23] 1.7시간 10,000
1958년 5월 조지 E. 펠턴 페가수스 컴퓨터(런던) 33시간 10,021
1959 프랑수아 지누이스 IBM 704(파리)[24] 4.3시간 16,167
1961 대니얼 샨크스 존 렌치 IBM 7090(뉴욕)[25] 8.7시간 100,265
1961 J.M. 제라드 IBM 7090(런던) 39분 20,000
1966 장 길루드와 J. 필리어트 IBM 7030(파리) 28시간[failed verification] 250,000
1967 장 기요드와 M. 디캄프트 CDC 6600(파리) 28시간 500,000
1973 장 기요드와 마르틴 부이어 CDC 7600 23.3시간 1,001,250
1981 미요시 가즈노리, 가나다 야스마사 FACOM M-200 2,000,036
1981 장 길루드 알 수 없음 2,000,050
1982 다무라 요시아키 멜컴 900II 2,097,144
1982 다무라 요시아키와 가나다 야스마사 HITAC M-280h 2.9시간 4,194,288
1982 다무라 요시아키와 가나다 야스마사 HITAC M-280h 8,388,576
1983 가나다 야스마사, 요시노 사야카, 다무라 요시아키 HITAC M-280h 16,777,206
1983년 10월 우시로 야스노리와 가나다 야스마사 HITAC S-810/20 10,013,395
1985년 10월 빌 고스퍼 기호학 3670 17,526,200
1986년 1월 데이비드 H. 베일리 CRAY-2 29,360,111
1986년 9월 가나다 야스마사, 다무라 요시아키 HITAC S-810/20 33,554,414
1986년 10월 가나다 야스마사, 다무라 요시아키 HITAC S-810/20 67,108,839
1987년 1월 가나다 야스마사, 다무라 요시아키, 쿠보 요시노부 등 NEC SX-2 134,214,700
1988년 1월 가나다 야스마사, 다무라 요시아키 HITAC S-820/80 201,326,551
1989년 5월 그레고리 5세 추드노브스키 & 데이비드 5세 추드노브스키 CRAY-2 & IBM 3090/VF 480,000,000
1989년 6월 그레고리 5세 추드노브스키 & 데이비드 5세 추드노브스키 IBM 3090 535,339,270
1989년 7월 가나다 야스마사, 다무라 요시아키 HITAC S-820/80 536,870,898
1989년 8월 그레고리 5세 추드노브스키 & 데이비드 5세 추드노브스키 IBM 3090 1,011,196,691
1989년 11월 19일 가나다 야스마사, 다무라 요시아키 HITAC S-820/80 1,073,740,799
1991년 8월 그레고리 5세 추드노브스키 & 데이비드 5세 추드노브스키 홈메이드 병렬 컴퓨터(자세한 내용은 알 수 없음, 확인되지 않음) 2,260,000,000
1994년 5월 18일 그레고리 5세 추드노브스키 & 데이비드 5세 추드노브스키 새 홈메이드 병렬 컴퓨터(자세한 내용은 알 수 없음, 확인되지 않음) 4,044,000,000
1995년 6월 26일 카나다 야스마사, 다카하시 다이스케 HITAC S-3800/480(이중 CPU) 3,221,220,000
1995 사이먼 플로프 다음을 허용하는 공식 찾기 n앞의 숫자를 계산하지 않고 계산할 파이 16진수 숫자.
1995년 8월 28일 카나다 야스마사, 다카하시 다이스케 HITAC S-3800/480(이중 CPU) 4,294,960,000
1995년 10월 11일 카나다 야스마사, 다카하시 다이스케 HITAC S-3800/480(이중 CPU) 6,442,450,000
1997년 7월 6일 카나다 야스마사, 다카하시 다이스케 Hitachi SR2201(1024 CPU) 51,539,600,000
1999년 4월 5일 카나다 야스마사, 다카하시 다이스케 Hitachi SR8000(128개 노드 중 64개) 68,719,470,000
1999년 9월 20일 카나다 야스마사, 다카하시 다이스케 Hitachi SR8000/MPP(128 노드) 206,158,430,000
2002년 11월 24일 카나다 야스마사 & 9인팀 HITHITCH SR8000/MPP(64개 노드), 일본[33] 도쿄 도립 도쿄 대학 정보과학부 600시간 1,241,100,000,000
2009년 4월 29일 다카하시 다이스케 외 T2K Open Supercomputer(640 노드), 단일 노드 속도는 147.2기가플롭스, 컴퓨터 메모리는 13.5테라바이트, 가우스-레젠더 알고리즘, 일본[34] 츠쿠바에 있는 츠쿠바 대학 컴퓨터 과학 센터 29.09시간 2,576,980,377,524

2009-현재

날짜 누구 실행 시간 소수점
( 굵게 표시된 세계 기록)
2009년 12월 이후의 모든 기록은 상용화된 부품이 있는 서버 및/또는 가정용 컴퓨터에서 계산되고 검증된다.
2009년 12월 31일 파브리스 벨라드
  • 코어 i7 CPU 2.93GHz
  • RAM 6 GiB(1)
  • 1.5TB 하드 디스크 5개를 사용한 7.5TB의 디스크 스토리지(Barracuda 7200.11 모델 참조)
  • 64비트 Red Hat Fedora 10 분포
  • 이진수 계산: 103일
  • 이진수 확인: 13일
  • 기준 10: 12일로 변환
  • 전환 확인: 3일
  • 34시간 동안 9대의 데스크톱 PC 네트워크를 사용한 이진수 확인, 추드노브스키 알고리즘, Bellard의 홈페이지 참조.[36]
 131일 2,699,999,990,000
2010년 8월 2일 곤도[37] 시게루
  • Alexander Yee의 y-cruncher[38] 사용
  • 추드노브스키 알고리즘은 주요 계산에 사용되었다.
  • 검증은 다른 컴퓨터에서 Bellard & Plouffe 공식을 사용했으며, 둘 다 4,152,410,118,610번째 16진수로 끝나는 32개의 16진수를 계산했다.
  • 2배 Intel Xeon X5680 @ 3.33GHz – (물리적 코어 12개, 하이퍼스레드 24개)
  • 96GiB DDR3 @ 1066MHz – (12×8GiB – 6채널) – 삼성(M393B1K70BH1)
  • 1TB SATA II(부팅 드라이브) – Hitachi(HDS721010CLA332), 2TB SATA II(Store Pi Output) – Seagate(ST32000542)AS) 16× 2TB SATA II(Computation) – Seagate(ST32000641)AS)
  • Windows Server 2008 R2 Enterprise x64
  • 이진수 계산: 80일
  • 기준 10: 8.2일
  • 전환 확인 : 45.6시간
  • 이진수 확인: 64시간(1차), 66시간(2차)
  • 2진수 확인은 주 연산 중에 두 개의 분리된 컴퓨터에서 동시에 수행되었다.[39]
 90일 5,000,000,000,000
2011년 10월 17일 곤도[40] 시게루
  • Alexander Yee의 y-cruncher 사용
  • 검증: 1.86일, 4.94일
 371일 10,000,000,000,050
2013년 12월 28일 곤도[41] 시게루
  • Alexander Yee의 y-cruncher 사용
  • 2배의 Intel Xeon E5-2690 @ 2.9GHz – (물리적 코어 16개, 하이퍼스레드 32개)
  • 128 GiB DDR3 @ 1600MHz – 8× 16 GiB – 8 채널
  • Windows Server 2012 x64
  • 확인: 46시간
 94일 12,100,000,000,050
2014년 10월 8일 산돈 나시 반 네스 "후쿠온치"[42]
  • Alexander Yee의 y-cruncher 사용
  • 2배 Xeon E5-4650L @ 2.6GHz 사용
  • 192 GiB DDR3 @ 1333 MHz
  • 24시간 4TB + 30시간 3TB
  • 확인: 182시간
 208일 13,300,000,000,000
2016년 11월 11일 피터 트루브[43][44]
  • Alexander Yee의 y-cruncher 사용
  • 4×Xeon E7-8890 v3 @ 2.50GHz(72 코어, 144 스레드) 사용
  • 1.25TiB DDR4
  • 20배 6TB
  • 확인: 28시간[45]
 105일 22,459,157,718,361
= ⌊πe × 1012⌋
2019년 3월 14일 이와오 엠마 하루카[46]
  • y 크런처 v0.7.6 사용
  • 계산: 1× n1-메가엠-96(96 vCPU, 1.4)TB) 30TB SSD 포함
  • 스토리지: 10TB SSD로 24배 n1-standard-16(16vCPU, 60GB)
  • 검증: Bellard의 7기 BBP 공식으로 20시간, Pluffe의 4기 BBP 공식으로 28시간 사용
 121일 31,415,926,535,897
= ⌊π × 1013⌋
2020년 1월 29일 티머시 멀리칸[47][48]
  • y 크런처 v0.7.7 사용
  • 계산: Intel Xeon CPU E7-4880 v2 @ 2.50GHz
  • 320GB DDR3 PC3-8500R ECC RAM
  • 48배 6TB HDD(Computation) + 47배 LTO Ultrium 5.5TB 테이프(Checkpoint Backup) + 12배 4TB HDD(자리 스토리지)
  • 검증: 벨라드 7기 BBP 공식 사용 17시간, 플로프의 4기 BBP 공식 사용 24시간
 303일 50,000,000,000,000
2021년 8월 14일 응용과학대학의[49][50] DAViS 팀
  • y 크런처 v0.7.8 사용
  • 연산: AMD Epyc 7542 @ 2.9GHz
  • 1TiB의 메모리
  • 38배 16TB HDD(이 중 24개는 스와핑에, 4개는 스토리지에 사용됨)
  • 검증: Bellard의 4기 BBP 공식 사용 34시간
 108일 62,831,853,071,796
= ⌊2π × 1013⌋

참고 항목

참조

  1. ^ "Validation File". Retrieved 2021-09-12.
  2. ^ a b c d e f g h i j k l m n o p q r s t u v w x y David H. Bailey, Jonathan M. Borwein, Peter B. Borwein & Simon Plouffe (1997). "The quest for pi" (PDF). Mathematical Intelligencer. 19 (1): 50–57. doi:10.1007/BF03024340. S2CID 14318695.CS1 maint: 작성자 매개변수 사용(링크)
  3. ^ Eggeling, Julius (1882–1900). The Satapatha-brahmana, according to the text of the Madhyandina school. Princeton Theological Seminary Library. Oxford, The Clarendon Press. pp. 302–303.CS1 maint: 날짜 및 연도(링크)
  4. ^ The Sacred Books of the East: The Satapatha-Brahmana, pt. 3. Clarendon Press. 1894. p. 303. Public Domain 이 글은 공개 도메인에 있는 이 출처의 텍스트를 통합한다..
  5. ^ "4 II. Sulba Sutras". www-history.mcs.st-and.ac.uk.
  6. ^ a b c d e f Ravi P. Agarwal, Hans Agarwal & Syamal K. Sen (2013). "Birth, growth and computation of pi to ten trillion digits". Advances in Difference Equations. 2013: 100. doi:10.1186/1687-1847-2013-100.CS1 maint: 작성자 매개변수 사용(링크)
  7. ^ Plofker, Kim (2009). Mathematics in India. Princeton University Press. p. 18. ISBN 978-0691120676.
  8. ^ https://www.math.rutgers.edu/~cherlin/History/Paper2000/wilson.html
  9. ^ 趙良五 (1991). 中西數學史的比較. 臺灣商務印書館. ISBN 978-9570502688 – via Google Books.
  10. ^ 니덤, 요셉(1986) 중국의 과학과 문명: 제3권, 수학과 천지의 과학. 타이베이: 코브스 북스 주식회사 제3권, 100권.
  11. ^ a b c 가장 가까운 소수점까지 반올림한다.
  12. ^ Bag, A. K. (1980). "Indian Literature on Mathematics During 1400–1800 A.D." (PDF). Indian Journal of History of Science. 15 (1): 86. π ≈ 2,827,433,388,233/9×10−11 = 3.14159 26535 92222..., good to 10 decimal places.
  13. ^ 약 2인치에서 9개의 성 소수 자릿수. 알카시, 저자: 아돌프 P. 유슈케비치, 수석 편집자: 보리스 A. 로젠펠트, 256쪽
  14. ^ Viète, François (1579). Canon mathematicus seu ad triangula : cum adpendicibus (in Latin).
  15. ^ Romanus, Adrianus (1593). Ideae mathematicae pars prima, sive methodus polygonorum (in Latin). apud Ioannem Keerbergium. hdl:2027/ucm.5320258006.
  16. ^ Grienbergerus, Christophorus (1630). Elementa Trigonometrica (PDF) (in Latin). Archived from the original (PDF) on 2014-02-01.
  17. ^ Hobson, Ernest William (1913). 'Squaring the Circle': a History of the Problem (PDF). Cambridge University Press. p. 27.
  18. ^ Yoshio, Mikami; Eugene Smith, David (2004) [1914]. A History of Japanese Mathematics (paperback ed.). Dover Publications. ISBN 0-486-43482-6.
  19. ^ Lopez-Ortiz, Alex (February 20, 1998). "Indiana Bill sets value of Pi to 3". the news.answers WWW archive. Department of Information and Computing Sciences, Utrecht University. Archived from the original on 2005-01-09. Retrieved 2009-02-01.
  20. ^ Reitwiesner, G. (1950). "An ENIAC determination of π and e to more than 2000 decimal places". MTAC. 4: 11–15. doi:10.1090/S0025-5718-1950-0037597-6.
  21. ^ Nicholson, S. C.; Jeenel, J. (1955). "Some comments on a NORC computation of π". MTAC. 9: 162–164. doi:10.1090/S0025-5718-1955-0075672-5.
  22. ^ G. E. Felton, "전자 컴퓨터와 수학자", 1957년 4월 8일–18일, 옥스포드 트리니티 칼리지에서 열린 학교 교사와 산업가를 위한 옥스포드 수학 회의의 약칭 프로시저, 페이지 12–17, 각주 페이지 12–53. 이 발표된 결과는 펠튼이 1958년에 완성되었지만 분명히 미발표된 것으로 보이는 공식 (5)을 사용하여 두 번째 계산에서 확립한 것처럼 7480D에 대해서만 정확하다. 계산에 대한 자세한 설명을 위해 π 보다
  23. ^ Genuys, F. (1958). "Dix milles decimales de π". Chiffres. 1: 17–22.
  24. ^ x ~ 16167D의 미발표 값은 Genuys의 프로그램을 통해 파리의 프랑스 대체 에너지 및 원자력 위원회의 IBM 704 시스템에서 계산되었다.
  25. ^ Shanks, Daniel; Wrench, John W. J.r (1962). "Calculation of π to 100,000 decimals". Mathematics of Computation. 16 (77): 76–99. doi:10.1090/S0025-5718-1962-0136051-9.
  26. ^ 더 큰 조각의 Pi (pi의 숫자 값은 21억 6천만 소수 자릿수에 이른다) 사이언스 뉴스 1991년 8월 24일 http://www.encyclopedia.com/doc/1G1-11235156.html
  27. ^ ftp://pi.super-computing.org/README.our_last_record_3b
  28. ^ ftp://pi.super-computing.org/README.our_last_record_4b
  29. ^ ftp://pi.super-computing.org/README.our_last_record_6b
  30. ^ ftp://pi.super-computing.org/README.our_last_record_51b
  31. ^ ftp://pi.super-computing.org/README.our_last_record_68b
  32. ^ ftp://pi.super-computing.org/README.our_latest_record_206b
  33. ^ "Archived copy". Archived from the original on 2011-03-12. Retrieved 2010-07-08.CS1 maint: 제목으로 보관된 복사본(링크)
  34. ^ "Archived copy". Archived from the original on 2009-08-23. Retrieved 2009-08-18.CS1 maint: 제목으로 보관된 복사본(링크)
  35. ^ "Fabrice Bellard's Home Page". bellard.org. Retrieved 28 August 2015.
  36. ^ http://bellard.org/pi/pi2700e9/pipcrecord.pdf
  37. ^ "PI-world". calico.jp. Archived from the original on 31 August 2015. Retrieved 28 August 2015.
  38. ^ "y-cruncher – A Multi-Threaded Pi Program". numberworld.org. Retrieved 28 August 2015.
  39. ^ "Pi – 5 Trillion Digits". numberworld.org. Retrieved 28 August 2015.
  40. ^ "Pi – 10 Trillion Digits". numberworld.org. Retrieved 28 August 2015.
  41. ^ "Pi – 12.1 Trillion Digits". numberworld.org. Retrieved 28 August 2015.
  42. ^ "y-cruncher – A Multi-Threaded Pi Program". numberworld.org. Retrieved 14 March 2018.
  43. ^ "pi2e". pi2e.ch. Retrieved 15 November 2016.
  44. ^ Alexander J. Yee. "y-cruncher – A Multi-Threaded Pi Program". numberworld.org. Retrieved 15 November 2016.
  45. ^ "Hexadecimal Digits are Correct! – pi2e trillion digits of pi". pi2e.ch. 31 October 2016. Retrieved 15 November 2016.
  46. ^ "Google Cloud Topples the Pi Record". Retrieved 14 March 2019.
  47. ^ "The Pi Record Returns to the Personal Computer". Retrieved 30 January 2020.
  48. ^ "Calculating Pi: My attempt at breaking the Pi World Record". 26 June 2019. Retrieved 30 January 2020.
  49. ^ "Pi-Challenge - world record attempt by UAS Grisons - University of Applied Sciences of the Grisons". www.fhgr.ch. 2021-08-14. Retrieved 2021-08-17.
  50. ^ "Die FH Graubünden kennt Pi am genauesten – Weltrekord! - News - FH Graubünden". www.fhgr.ch (in German). 2021-08-16. Retrieved 2021-08-17.

외부 링크