메타휴리스틱

Metaheuristic

컴퓨터 과학 및 수학적 최적화에서 메타 휴리스틱은 특히 불완전하거나 불완전한 정보 또는 제한된 계산 [1][2]능력으로 최적화 문제에 대해 충분히 좋은 해결책을 제공할 수 있는 휴리스틱(부분 검색 알고리즘)을 발견, 생성 또는 선택하도록 설계된 높은 수준의 절차 또는 휴리스틱입니다.메타휴리스틱스는 너무 커서 완전히 열거하거나 탐구할 수 없는 솔루션의 서브셋을 샘플링합니다.메타 휴리스틱스는 해결 중인 최적화 문제에 대해 비교적 적은 가정을 할 수 있기 때문에 다양한 [3]문제에 사용할 수 있습니다.

최적화 알고리즘 및 반복 방법과 비교하여 메타 휴리스틱스는 특정 종류의 [3]문제에 대해 글로벌하게 최적의 솔루션을 찾을 수 있음을 보장하지 않습니다.많은 메타휴리스틱은 확률적 최적화의 형태를 구현하기 때문에 발견된 솔루션은 생성된 [2]랜덤 변수 집합에 의존합니다.조합 최적화에서 메타 휴리스틱스는 많은 실행 가능한 솔루션 세트를 검색함으로써 최적화 알고리즘, 반복 방법 또는 단순 [3]휴리스틱스보다 적은 계산 노력으로 좋은 솔루션을 찾을 수 있습니다.따라서 최적화 [2]문제에 대한 유용한 접근법입니다.그 [2][3][4][5][6]주제에 관한 여러 권의 책과 설문지가 출판되었다.

메타휴리스틱스에 관한 대부분의 문헌은 본질적으로 실험적인 것으로, 알고리즘에 의한 컴퓨터 실험에 근거한 경험적 결과를 기술하고 있다.그러나 종종 수렴과 글로벌 [3]최적화의 가능성에 대한 공식적인 이론적 결과도 이용할 수 있습니다.많은 메타휴리스틱 방법들이 참신성과 실용적 유효성에 대한 주장과 함께 출판되었다.이 분야는 또한 수준 높은 연구를 특징으로 하고 있지만, 많은 출판물들은 질이 낮습니다; 모호함, 개념적 정교함의 결여, 형편없는 실험, 그리고 이전 [7]문헌에 대한 무지함 등이 있습니다.

특성.

대부분의 메타 휴리스틱을 [3]특징짓는 속성은 다음과 같습니다.

  • 메타휴리스틱스는 검색 프로세스를 안내하는 전략입니다.
  • 목표는 검색 공간을 효율적으로 탐색하여 최적의 솔루션을 찾는 것입니다.
  • 메타휴리스틱 알고리즘을 구성하는 기술은 단순한 로컬 검색 절차에서 복잡한 학습 프로세스에 이르기까지 다양하다.
  • 메타 휴리스틱 알고리즘은 대략적이며 일반적으로 결정적이지 않습니다.
  • 메타 휴리스틱스는 문제 고유의 것이 아닙니다.

분류

메타휴리스틱스의 [8]다른 분류에 대한 오일러 다이어그램.

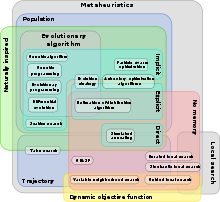
메타휴리스틱은[2] 매우 다양하며 [3]분류할 수 있는 특성도 많다.

로컬 검색 vs. 글로벌 검색

한 가지 방법은 검색 [3]전략의 유형을 특성화하는 것입니다.검색 전략의 한 가지 유형은 간단한 로컬 검색 알고리즘을 개선하는 것입니다.잘 알려진 로컬 검색 알고리즘은 로컬 최적점을 찾는 데 사용되는 언덕 오르기 방법입니다.하지만, 언덕을 오르는 것이 세계적인 최적의 해결책을 찾는 것을 보장하지는 않습니다.

보다 나은 해결책을 찾기 위해 로컬 검색 휴리스틱을 개선하기 위해 많은 메타 휴리스틱 아이디어가 제안되었다.이러한 메타 휴리스틱에는 시뮬레이트된 어닐링, tabu 검색, 반복된 로컬 검색, 가변 근린 검색 및 [3]TRAPP가 포함됩니다.이러한 메타휴리스틱은 로컬 검색 기반 또는 글로벌 검색 메타휴리스틱으로 분류할 수 있습니다.

로컬 검색 기반이 아닌 다른 전역 검색 메타 휴리스틱은 일반적으로 모집단 기반 메타 휴리스틱입니다.그러한 메타휴리스틱스에는 개미 군집 최적화, 진화 연산, 입자 군집 최적화, 유전 알고리즘, 라이더 최적화[9] 알고리즘 등이 포함된다.

싱글 솔루션과 모집단 기반

또 다른 분류 차원은 단일 솔루션과 모집단 기반 [3][6]검색입니다.단일 솔루션 접근방식은 단일 후보 솔루션의 수정과 개선에 중점을 두고 있습니다.단일 솔루션 메타 휴리스틱스에는 시뮬레이트된 어닐링, 반복 로컬 검색, 변수 인근 검색,[6] 가이드 로컬 검색이 포함됩니다.모집단 기반 접근방식은 여러 후보 솔루션을 유지하고 개선하며, 종종 모집단 특성을 사용하여 검색을 안내한다. 모집단 기반 메타휴리스틱에는 진화 계산, 유전 알고리즘 및 입자 군집 [6]최적화가 포함된다.메타휴리스틱스의 또 다른 범주는 집단 또는 집단에서 분산된 자기 조직화된 에이전트의 집단 행동인 군집 지능입니다.개미 군집 최적화,[10] 입자 군집 최적화,[6] 사회적 인지 최적화가 이 범주의 예입니다.

하이브리드화 및 메모리 알고리즘

하이브리드 메타 휴리스틱은 메타 휴리스틱을 수학적 프로그래밍, 제약 조건 프로그래밍 및 기계 학습의 알고리즘과 같은 다른 최적화 접근법과 결합하는 것입니다.하이브리드 메타 휴리스틱의 두 구성 요소는 동시에 실행되고 검색을 안내하기 위한 정보를 교환할 수 있습니다.

반면에, 메메틱 알고리즘은[11] 문제 검색을 위한 개별 학습 또는 국지적 개선 절차를 통해 진화적 또는 모집단 기반 접근법의 시너지 효과를 나타낸다.memetic 알고리즘의 예는 진화 알고리즘에서 기본 돌연변이 연산자 대신 로컬 검색 알고리즘을 사용하는 것입니다.

병렬 메타휴리스틱스

병렬 메타 휴리스틱은 병렬 프로그래밍 기술을 사용하여 여러 메타 휴리스틱 검색을 병렬로 실행하는 방법입니다. 단순 분산 방식부터 전체 솔루션을 개선하기 위해 상호 작용하는 동시 검색 실행까지 다양합니다.

자연에서 영감을 얻은 메타휴리스틱스

주요 기사:군집 지능 및 메타휴리스틱스 목록

자연에서 영감을 받은 메타휴리스틱스의 설계는 매우 활발한 연구 영역이다.최근의 많은 메타휴리스틱스, 특히 진화적 계산 기반 알고리즘은 자연 시스템에서 영감을 얻었다.자연은 복잡한 계산 문제를 다루기 위한 인공 컴퓨팅 시스템 설계의 개념, 메커니즘 및 원칙의 원천으로 작용합니다.이러한 메타휴리스틱스에는 시뮬레이션 어닐링, 진화 알고리즘, 개미 군집 최적화 및 입자 군집 최적화가 포함됩니다.보다 최근의 메타휴리스틱에서 영감을 받은 많은 메타휴리스틱들이 정교한 [7]은유 뒤에 그들의 참신함의 결여를 숨긴다는 이유로 연구 커뮤니티에서 비판을 받기 시작했다.

적용들

메타휴리스틱스는 이산 서치 공간에서 최적의 솔루션을 찾는 조합 최적화에 사용된다.문제의 예로는 여행중인 세일즈맨의 문제가 있습니다.문제 규모가 커짐에 따라 후보 솔루션의 검색 공간이 기하급수적으로 증가하기 때문에 최적의 솔루션을 철저히 검색할 수 없게 됩니다.또한 형태 검색 및 행동 검색과 같은 엔지니어링의[12][13][14] 대부분의 설계 문제를 포함한 다차원 조합 문제는 차원성의 저주로 인해 어려움을 겪으며, 이는 또한 완전한 검색 또는 분석 방법으로는 실현 불가능하게 만듭니다.메타휴리스틱은 또한 잡샵 스케줄링과 직업선택 [citation needed]문제에도 널리 사용된다.조합 문제에 대한 인기 있는 메타휴리스틱에는 커크패트릭 등의 시뮬레이션 어닐링,[15] 홀랜드 등의 유전자 알고리즘, 글로버의 산란[17] 검색 및 타부[18] 검색이 포함된다.[16]메타 휴리스틱 [19]최적화에 대한 문헌 리뷰는 메타 [20]휴리스틱스라는 단어를 만든 사람이 프레드 글로버라고 제안했다.

메타휴리스틱 최적화 프레임워크(MOF)

MOF는 ''메타 휴리스틱스 세트의 올바르고 재사용 가능한 구현을 제공하는 소프트웨어 도구 세트' 및 특정 문제를 해결하기 위해 필요한 파트너 하위 휴리스틱스(솔루션 인코딩 및 기술별 연산자 포함)의 구현을 가속화하는 기본 메커니즘'으로 정의할 수 있습니다.제공된 기술을 사용하는 nstance''[21]입니다.

다양한 기능의 MOF로 간주할 수 있는 최적화 도구는 다음과 같습니다.혜성, EvA2, Evolvica, 진화론:알고리즘, GAPlayground, jaga, JCLEC, JGAP, jMetal, n-genes, Open Beagle, Opt4j, ParadisEO/EO, Pisa, Watchmaker, FOM, Hypercube, HotFrame, 템플러, EasyLocal, iOpt, OptQuest, JDEAL, 최적화 알고리즘 툴킷, 휴리스틱 랩, MAFRA, Localizer, GALIB, DREAM, Discropt, MA, MA, Magma, Magma, Magma, Magma, Magma, Magma, Magma, Magma, Magma, Magma, Magma, Magma

투고

다양한 메타휴리스틱이 존재하며 새로운 변형이 지속적으로 제안되고 있다.이 분야에서 가장 중요한 공헌은 다음과 같습니다.

「 」를 참조해 주세요.

레퍼런스

  1. ^ R. Balamurugan; A.M. Natarajan; K. Premalatha (2015). "Stellar-Mass Black Hole Optimization for Biclustering Microarray Gene Expression Data". Applied Artificial Intelligence. 29 (4): 353–381. doi:10.1080/08839514.2015.1016391. S2CID 44624424.
  2. ^ a b c d e Bianchi, Leonora; Marco Dorigo; Luca Maria Gambardella; Walter J. Gutjahr (2009). "A survey on metaheuristics for stochastic combinatorial optimization" (PDF). Natural Computing. 8 (2): 239–287. doi:10.1007/s11047-008-9098-4. S2CID 9141490.
  3. ^ a b c d e f g h i j Blum, C.; Roli, A. (2003). "Metaheuristics in combinatorial optimization: Overview and conceptual comparison". 35 (3). ACM Computing Surveys: 268–308. {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)
  4. ^ Goldberg, D.E. (1989). Genetic Algorithms in Search, Optimization and Machine Learning. Kluwer Academic Publishers. ISBN 978-0-201-15767-3.
  5. ^ Glover, F.; Kochenberger, G.A. (2003). Handbook of metaheuristics. Vol. 57. Springer, International Series in Operations Research & Management Science. ISBN 978-1-4020-7263-5.
  6. ^ a b c d e Talbi, E-G. (2009). Metaheuristics: from design to implementation. Wiley. ISBN 978-0-470-27858-1.
  7. ^ a b Sörensen, Kenneth (2015). "Metaheuristics—the metaphor exposed" (PDF). International Transactions in Operational Research. 22: 3–18. CiteSeerX 10.1.1.470.3422. doi:10.1111/itor.12001. Archived from the original (PDF) on 2013-11-02.
  8. ^ 메타휴리스틱스의 분류
  9. ^ D, Binu (2019). "RideNN: A New Rider Optimization Algorithm-Based Neural Network for Fault Diagnosis in Analog Circuits". IEEE Transactions on Instrumentation and Measurement. 68 (1): 2–26. doi:10.1109/TIM.2018.2836058. S2CID 54459927.
  10. ^ a b M. Dorigo, Optimization, Learning and Natural Algorithm, PhD 논문, Politecnico di Milano, Italie, 1992.
  11. ^ a b Moscato, P. (1989). "On Evolution, Search, Optimization, Genetic Algorithms and Martial Arts: Towards Memetic Algorithms". Caltech Concurrent Computation Program (report 826).
  12. ^ 토모이아거 B, 친드리쉬 M, 섬퍼 A, 수드리아-안드레우 A, 빌라필라-로블레스 R.NSGA-II. 에너지에 기반한 유전 알고리즘을 이용한 배전 시스템의 파레토 최적 재구성2013; 6(3):1439–1455.
  13. ^ Ganesan, T.; Elamvazuthi, I.; Ku Shaari, Ku Zilati; Vasant, P. (2013-03-01). "Swarm intelligence and gravitational search algorithm for multi-objective optimization of synthesis gas production". Applied Energy. 103: 368–374. doi:10.1016/j.apenergy.2012.09.059.
  14. ^ Ganesan, T.; Elamvazuthi, I.; Vasant, P. (2011-11-01). Evolutionary normal-boundary intersection (ENBI) method for multi-objective optimization of green sand mould system. 2011 IEEE International Conference on Control System, Computing and Engineering (ICCSCE). pp. 86–91. doi:10.1109/ICCSCE.2011.6190501. ISBN 978-1-4577-1642-3. S2CID 698459.
  15. ^ a b Kirkpatrick, S.; Gelatt Jr., C.D.; Vecchi, M.P. (1983). "Optimization by Simulated Annealing". Science. 220 (4598): 671–680. Bibcode:1983Sci...220..671K. CiteSeerX 10.1.1.123.7607. doi:10.1126/science.220.4598.671. PMID 17813860. S2CID 205939.
  16. ^ a b Holland, J.H. (1975). Adaptation in Natural and Artificial Systems. University of Michigan Press. ISBN 978-0-262-08213-6.
  17. ^ a b Glover, Fred (1977). "Heuristics for Integer programming Using Surrogate Constraints". Decision Sciences. 8 (1): 156–166. CiteSeerX 10.1.1.302.4071. doi:10.1111/j.1540-5915.1977.tb01074.x.
  18. ^ a b Glover, F. (1986). "Future Paths for Integer Programming and Links to Artificial Intelligence". Computers and Operations Research. 13 (5): 533–549. doi:10.1016/0305-0548(86)90048-1.
  19. ^ X. S. Yang, 메타휴리스틱 최적화, Scholarpedia, 6(8):11472(2011).
  20. ^ 글로버 F., (1986)정수 프로그래밍 및 인공지능, 컴퓨터 및 운영 연구, 13, 533–549(1986)와의 연결을 위한 미래 경로.
  21. ^ a b Moscato, P. (2012). "Metaheuristic optimization frameworks a survey and benchmarking". Soft Comput. 16 (3): 527–561. doi:10.1007/s00500-011-0754-8. hdl:11441/24597. S2CID 1497912.
  22. ^ Robbins, H.; Monro, S. (1951). "A Stochastic Approximation Method" (PDF). Annals of Mathematical Statistics. 22 (3): 400–407. doi:10.1214/aoms/1177729586.
  23. ^ Barricelli, N.A. (1954). "Esempi numerici di processi di evoluzione". Methodos: 45–68.
  24. ^ Rastrigin, L.A. (1963). "The convergence of the random search method in the extremal control of a many parameter system". Automation and Remote Control. 24 (10): 1337–1342.
  25. ^ Matyas, J. (1965). "Random optimization". Automation and Remote Control. 26 (2): 246–253.
  26. ^ Nelder, J.A.; Mead, R. (1965). "A simplex method for function minimization". Computer Journal. 7 (4): 308–313. doi:10.1093/comjnl/7.4.308. S2CID 2208295.
  27. ^ Rechenberg, Ingo (1965). "Cybernetic Solution Path of an Experimental Problem". Royal Aircraft Establishment, Library Translation.
  28. ^ Fogel, L.; Owens, A.J.; Walsh, M.J. (1966). Artificial Intelligence through Simulated Evolution. Wiley. ISBN 978-0-471-26516-0.
  29. ^ Hastings, W.K. (1970). "Monte Carlo Sampling Methods Using Markov Chains and Their Applications". Biometrika. 57 (1): 97–109. Bibcode:1970Bimka..57...97H. doi:10.1093/biomet/57.1.97. S2CID 21204149.
  30. ^ Cavicchio, D.J. (1970). "Adaptive search using simulated evolution". Technical Report. University of Michigan, Computer and Communication Sciences Department. hdl:2027.42/4042.
  31. ^ Kernighan, B.W.; Lin, S. (1970). "An efficient heuristic procedure for partitioning graphs". Bell System Technical Journal. 49 (2): 291–307. doi:10.1002/j.1538-7305.1970.tb01770.x.
  32. ^ Mercer, R.E.; Sampson, J.R. (1978). "Adaptive search using a reproductive metaplan". Kybernetes. 7 (3): 215–228. doi:10.1108/eb005486.
  33. ^ Smith, S.F. (1980). A Learning System Based on Genetic Adaptive Algorithms (PhD Thesis). University of Pittsburgh.
  34. ^ Moscato, P.; Fontanari, J.F. (1990), "Stochastic versus deterministic update in simulated annealing", Physics Letters A, 146 (4): 204–208, Bibcode:1990PhLA..146..204M, doi:10.1016/0375-9601(90)90166-L
  35. ^ Dueck, G.; Scheuer, T. (1990), "Threshold accepting: A general purpose optimization algorithm appearing superior to simulated annealing", Journal of Computational Physics, 90 (1): 161–175, Bibcode:1990JCoPh..90..161D, doi:10.1016/0021-9991(90)90201-B, ISSN 0021-9991
  36. ^ Wolpert, D.H.; Macready, W.G. (1995). "No free lunch theorems for search". Technical Report SFI-TR-95-02-010. Santa Fe Institute. S2CID 12890367.
  37. ^ Igel, Christian, Toussaint, Marc (Jun 2003). "On classes of functions for which No Free Lunch results hold". Information Processing Letters. 86 (6): 317–321. arXiv:cs/0108011. doi:10.1016/S0020-0190(03)00222-9. ISSN 0020-0190. S2CID 147624.{{cite journal}}: CS1 maint: 여러 이름: 작성자 목록(링크)
  38. ^ Auger, Anne, Teytaud, Olivier (2010). "Continuous Lunches Are Free Plus the Design of Optimal Optimization Algorithms". Algorithmica. 57 (1): 121–146. CiteSeerX 10.1.1.186.6007. doi:10.1007/s00453-008-9244-5. ISSN 0178-4617. S2CID 1989533.{{cite journal}}: CS1 maint: 여러 이름: 작성자 목록(링크)
  39. ^ Stefan Droste; Thomas Jansen; Ingo Wegener (2002). "Optimization with Randomized Search Heuristics – The (A)NFL Theorem, Realistic Scenarios, and Difficult Functions". Theoretical Computer Science. 287 (1): 131–144. CiteSeerX 10.1.1.35.5850. doi:10.1016/s0304-3975(02)00094-4.

추가 정보

  • Sörensen, Kenneth; Sevaux, Marc; Glover, Fred (2017-01-16). "A History of Metaheuristics" (PDF). In Martí, Rafael; Panos, Pardalos; Resende, Mauricio (eds.). Handbook of Heuristics. Springer. ISBN 978-3-319-07123-7.
  • Ashish Sharma(2022), 랜덤화된 하이퍼컴퓨팅 관점을 가진 자연에서 영감을 얻은 알고리즘.정보과학https://doi.org/10.1016/j.ins.2022.05.020 를 참조해 주세요.

외부 링크