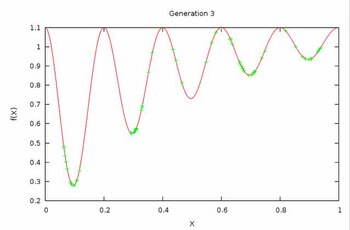
진화적 다중모드 최적화

다음 시리즈의 일부
진화 알고리즘
인공발달성 인공생명체 세포진화 알고리즘 문화 알고리즘 미분진화 효과적인 피트니스 진화 연산 진화전략 가우스 적응 진화적 다중모드 최적화 입자 군집 최적화 메미틱 알고리즘 자연 진화 전략 신경진화 프로모터 기반 유전 알고리즘 나선 최적화 알고리즘 자체수정코드 다형 코드
유전 알고리즘
염색체 클론 선택 알고리즘 크로스오버 돌연변이 유전적 기억력 유전 퍼지 시스템 선택 플라이 알고리즘
유전자 프로그래밍
데카르트 유전 프로그래밍 선형유전자프로그래밍 문법적 진화 다중 표현식 프로그래밍 유전적 개선 스키마 유리스코 패리티 벤치마크
v t

응용수학에서 다중모달 최적화는 단일 최선의 해결책이 아니라 문제의 다중(최소한 국지적으로 최적) 해결책의 전부 또는 대부분을 찾는 것을 포함하는 최적화 과제를 다룬다. 진화적 다중모드 최적화는 기계학습과 밀접한 관련이 있는 진화적 계산의 한 분야다. 웡은 ^[1]셜의^[2] 장과 프루스의^[3] 책에서 주제를 더 자세히 다룬 짧은 설문조사를 제공한다.

동기

최적화 작업에 대한 다중 솔루션에 대한 지식은 특히 엔지니어링에 유용하다. 물리적(및/또는 비용) 제약으로 인해 최상의 결과가 항상 실현 가능하지는 않을 수 있다. 그러한 시나리오에서 복수의 솔루션(로컬 및/또는 글로벌 최적)이 알려진 경우, 구현을 다른 솔루션으로 빠르게 전환하고 여전히 가능한 최상의 시스템 성능을 얻을 수 있다. 또한 여러 솔루션을 분석하여 기본 최적화 문제의 숨겨진 속성(또는 관계)을 발견할 수 있어 도메인 지식 획득에 중요한 역할을 할 수 있다. 또한, 멀티모달 최적화를 위한 알고리즘은 일반적으로 한 번의 실행으로 복수의 최적점을 찾을 뿐만 아니라, 그 모집단의 다양성을 보존하여 멀티모달 기능에 대한 글로벌 최적화 능력을 갖게 된다. 더욱이 다중모드 최적화를 위한 기법은 대개 다른 문제에 대한 다양성 유지 기법으로 차용된다.^[4]

배경

그러나 고전적인 최적화 기법에는 매번 다른 해결책이 발견될 수 있다는 희망으로 다중 재시작 지점과 다중 실행이 필요할 수 있다. 인구 기반 접근방식으로 인한 진화 알고리즘(EAs)은 고전적 최적화 기법보다 자연스러운 이점을 제공한다. 그들은 모든 세대에 걸쳐 처리되는 가능한 해결책의 집단을 유지하며, 만약 다중 해결책이 이 모든 세대에 걸쳐 보존될 수 있다면, 알고리즘이 종료될 때 우리는 최선의 해결책만이 아니라 여러 가지 좋은 해결책을 갖게 될 것이다. 이는 고전적 최적화 기법의 자연적 경향에 반하는 것으로, 이는 항상 최상의 솔루션 또는 차선의 솔루션(강박하고 "나쁜" 기능)으로 수렴된다는 점에 유의한다. 멀티모드 최적화를 위해 EA를 사용하는 것이 당면 과제인 다중 솔루션 찾기 및 유지보수가 그것이다. Niching은^[5] 단일 솔루션으로의 정합화를 방지하기 위해 복수의 안정적인 틈새 또는 복수의 솔루션 주변에서 유리한 부분을 찾아 보존하는 기법이라고 하는 총칭이다.

진화 알고리즘 분야는 유전 알고리즘(GA), 진화 전략(ES), 미분 진화(DE), 입자 군집 최적화(PSO), 기타 방법을 포괄한다. 이러한 모든 영역과 대부분의 영역에서 멀티모달 최적화를 해결하려는 시도가 있었으며, 모든 다양한 방법이 니칭을 어떤 형태로든 구현하지는 않는다.

유전자 알고리즘/진화 전략을 사용한 멀티모달 최적화

드종의 혼잡법, 골드버그의 공유기능 접근법, 페트로스키의 정리법, 짝짓기 제한, 다수의 하위집단 유지 등은 공동체가 제안해 온 인기 있는 접근법 중 하나이다. 처음의 두 방법은 특히 잘 연구되어 있지만, 서로 다른 유인원에 속하는 해결책으로 명시적으로 분리되지 않는다.

ES 내 멀티모달 최적화의 적용은 수년 동안 명시되지 않았으며, 최근에야 탐구되었다. 셜이 CMA-ES를 니칭 옵티마이저로 처음 제안하면서, ^[6]셜에 의해 비안도화된 ES를 활용한 니칭 프레임워크가 도입되었다. 그 프레임워크의 밑바탕은 각 세대의 하위 인구당 피크 개인을 선택한 다음, 검색 지점의 연속적인 분산을 산출하기 위한 표본 추출이었다. 이 기계의 생물학적 유사점은 알파 남성이 부과된 모든 대회에서 우승하고 그 이후 그것의 생태학적 틈새에서 지배하는 것으로, 그 후 모든 성적 자원을 얻어 그 자손을 만들어낸다.

최근, 진화론적 다목적적 다중모드 최적화(EMO)^[7] 접근방식이 제안되었는데, 이 접근방식은 원래 단일 목표 다중모드 최적화 문제에 적합한 두 번째 목표가 추가되어, 복수의 솔루션이 취약한 pareto-최적화 전선을 형성한다. 따라서, 다중모달 최적화 문제는 EMO 알고리즘을 사용하여 여러 솔루션에 대해 해결할 수 있다. 그들의 작업을 개선하면서,^[8] 같은 저자들이 알고리즘을 자기 적응적으로 만들었고, 따라서 매개변수를 미리 지정할 필요가 없어졌다.

모집단을 하위 모집단(또는 종)으로 분리하기 위해 반지름을 사용하지 않고 대신 공간 토폴로지를 사용하는 접근법이 제안된다.^[9]

참조

참고 문헌 목록

외부 링크

• PSO(입자 군집 최적화)를 이용한 멀티모달 최적화
• 진화 전략의 니칭(Niching in Evolution Strategies)
• TU 도르트문트대학교 컴퓨터과학 11번 강좌의 멀티모달 최적화 페이지
• 다중모드 최적화에 대한 IEEE CIS 태스크포스