스핀양자수
Spin quantum number이 기사는 대부분의 독자들이 이해하기에는 너무 기술적일 수 있습니다.인 세부사항을 할 수 을 바랍니다. (2024년 2월)(본 및 |
스핀양자수(spin quantum number)는 물리학에서 전자나 다른 입자의 고유한 각운동량(또는 스핀 각운동량, 간단히 스핀)을 기술하는 양자수(지정된 수)입니다. =와 같은 동일한 유형의 모든 입자에 대해 동일한 값을 갖습니다. 모든 전자에 대해 1/2. 광자와 같은 모든 보손에 대한 정수이고, 전자와 양성자와 같은 모든 페르미온에 대한 반홀수 정수입니다.
지정된 축을 따른 스핀의 성분은 전통적으로 m이라고s 쓰여진 스핀 자기 양자수에 의해 주어집니다.[1][2] m의 값은 주어진 방향에 평행한 감소된 플랑크 상수 ħ 단위로 스핀 각운동량의 구성 요소입니다(일반적으로 z축이라고 함). +s ~ -s 범위의 값을 정수 단위로 사용할 수 있습니다. 전자의 경우 m은s ++1/2 또는 -+1/2일 수 있습니다.
명명법
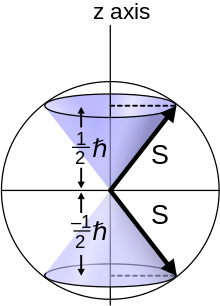
스핀 양자수라는 말은 양자화된 스핀 각운동량을 말합니다. 기호는 스핀 양자수에 사용되며, m은s 스핀 자기 양자수[3] 또는 스핀의z z 성분으로 설명됩니다.[4]
총 스핀과 스핀의 z 성분이 모두 양자화되어 두 개의 양자수 스핀과 스핀 자석 양자수가 생성됩니다.[5] 모든 기본 입자에 대해 단 하나의 값으로서 (총) 스핀 양자수. 화학 입문 교재 중에는 스핀s 양자수라고 설명하는 것도 있고,[6][7] 그 값이 전자의 고정된 성질이기 때문에 s는 언급되지 않고 있고, 심지어s m 대신 변수를 사용하는 것도 있습니다.[5]
두 스핀 및 는 두 궤도 각운동량 l 및 의 스핀 각운동량 유사체입니다[8]: 152
스핀 양자수는 하나 이상의 전자를 포함할 수 있는 원자와 같은 결합된 스핀 시스템에도 적용됩니다. 대문자 기호가 사용됩니다: 전체 전자 스핀의 경우 S, z축 성분의 경우S m 또는S M. 스핀 싱글렛 상태의 전자쌍은 S = 0이고, 트리플렛 상태의 전자쌍은 S = 1이며, m = -1, 0, 또는 +1입니다. 일반적으로 핵-스핀 양자수는 스핀에 대해 I, z축 성분에 대해 mI 또는 M으로I 표기됩니다.
"스핀"이라는 이름은 울렌벡과 가우즈밋이 제안한 것처럼 전자가 한 축을 중심으로 기하학적으로 회전한 데서 유래했습니다. 그러나 이 단순한 그림은 빛의 속도보다 전자가 더 빨리 회전해야 하기 때문에 물리적으로 비현실적이라는 것을 빠르게 깨달았습니다.[9] 따라서 더 추상적인 양자역학적 설명으로 대체되었습니다.
역사
1916년에서 1925년 사이의 기간 동안 주기율표에서 전자의 배열과 관련하여 많은 진전이 있었습니다. 조머펠트는 보어 원자의 지만 효과를 설명하기 위해 전자가 궤도의 크기, 궤도의 모양, 궤도가 가리키는 방향을 설명하는 세 가지 '양자수'에 기초할 것을 제안했습니다.[10] 어빙 는 1919년 논문에서 껍질에 있는에 대해 "리드버그는 이 숫자들이 = (+ + + + 열에서 얻어진다고 지적했습니다라고 설명했습니다 인자 2는 모든 안정한 원자에 대한 근본적인 이중 대칭을 시사합니다."[11] 이 구성은 1924년 10월 에드먼드 스토너가 철학 잡지에 발표한 논문 '원자 준위 간 전자의 분포'에서 채택했습니다. 볼프강 파울리는 이것이 두 값을 가지는 네 번째 양자수를 필요로 한다는 가설을 세웠습니다.[12]
전자 스핀
스핀-1/2 입자는 스핀에 대한 각운동량 양자수 = 1/2로 특징지어집니다. 슈뢰딩거-파울리 방정식의 해에서는 이 수에 따라 각운동량이 양자화되므로 스핀 각운동량의 크기는
수소 스펙트럼 미세 구조는 각운동량의 z 성분에 대한 두 가지 가능성에 해당하는 이중선으로 관찰되며, 여기서 임의의 방향 z에 대해서는 다음과 같습니다.
전자에 대해 가능한 두 개의 z compon 변수만을 갖는 용액입니다. 전자에서는 두 가지 다른 스핀 방향을 "스핀업" 또는 "스핀다운"이라고 부르기도 합니다.
전자의 스핀 특성은 네 번째 양자수에 필요한 자기 모멘트를 발생시킵니다.
전자 스핀의 자기 모멘트 벡터는 다음과 같습니다.
서 e 는 전자 전하, m 은 전자 질량, 는 전자 스핀 g-팩터로 약 2.0023입니다. z축 투영은 다음에 따라 스핀 자기 양자 m 에 의해 제공됩니다.
서 μ _는 보어 마그네톤입니다.
원자에 짝수 개의 전자가 있을 때, 각 궤도에 있는 각 전자의 스핀은 바로 옆에 있는 전자의 스핀과 반대 방향을 갖습니다. 그러나 많은 원자들은 홀수 개의 전자를 가지고 있거나, 짝수 개의 "돌려진" 방향과 "돌려진" 방향이 일치하지 않는 전자 배열을 가지고 있습니다. 이 원자나 전자는 전자 스핀 공명에서 검출되는 짝을 이루지 않은 스핀을 가지고 있다고 합니다.
핵스핀
원자핵에도 스핀이 있습니다. 핵스핀 I은 각 핵의 고정된 성질이며 정수 또는 반정수일 수 있습니다. z축에 평행한 핵스핀의 성분 m은 (2I + 1) I, I–1, ..., -I 값을 가질 수 있습니다. 예를 들어, N개의 핵은 I = 1이므로 상태 m = +1, 0, -1에 해당하는 z축에 대해 3개의 가능한 방향이 있습니다.
다른 핵의 스핀 I은 핵 껍질 모델을 사용하여 해석됩니다. 양성자와 중성자가 짝수 개인 짝수 개의 핵, 예를 들어 C와 O는 스핀이 0입니다. 홀수 질량수 핵은 Li의 경우 3/2, C의 경우 1/2, O의 경우 5/2와 같이 반 정수의 스핀을 가지며, 일반적으로 마지막으로 추가된 핵의 각운동량에 해당합니다. 양성자와 중성자가 모두 홀수인 홀수 핵은 정수 스핀을 갖는데, 예를 들어 B의 경우 3, N의 경우 1이 있습니다.[14] 주어진 동위원소에 대한 핵 스핀 값은 각 원소의 동위원소 목록에서 확인할 수 있습니다. (산소 동위원소, 알루미늄 동위원소 등 참조)
스핀 검출
수소 스펙트럼의 선을 매우 고해상도로 조사했을 때, 그것들은 밀접하게 이격된 이중선으로 밝혀졌습니다. 이 분열은 미세 구조라고 불리며, 전자 스핀에 대한 최초의 실험적 증거 중 하나였습니다. 전자의 고유 각운동량을 직접 관찰한 것은 스턴-게를라흐 실험에서 이루어졌습니다.
스턴-게를라흐 실험
자기장 안에 위치한 원자의 전자 운동량 스핀 모멘트의 공간 양자화 이론은 실험적으로 증명될 필요가 있었습니다. 1922년 (스핀에 대한 이론적 설명이 만들어지기 2년 전) 오토 스턴(Otto Stern)과 월터 게를라흐(Walter Gerlach)는 그들이 수행한 실험에서 그것을 관찰했습니다.
진공에서 전기로를 사용하여 은 원자를 증발시켰습니다. 얇은 슬릿을 사용하여 원자를 평평한 빔으로 유도하고 빔을 균일하지 않은 자기장을 통해 보낸 후 금속판과 충돌시켰습니다. 고전물리학의 법칙들은 판 위의 응축된 은 원자들의 집합체가 원래의 빔과 같은 모양으로 가는 실선을 형성해야 한다고 예측합니다. 그러나 균일하지 않은 자기장으로 인해 빔이 두 개의 서로 다른 방향으로 갈라져 금속판에 두 개의 선이 생성되었습니다.
이 현상은 운동량 스핀 모멘트의 공간 양자화로 설명할 수 있습니다. 원자에서 전자는 하나가 위쪽과 아래쪽으로 회전하도록 쌍을 이루어 원자 전체의 작용에 대한 스핀의 영향을 중화합니다. 하지만 은 원자의 원자가 껍질에는 스핀이 불균형하게 유지되는 단일 전자가 있습니다.
불균형한 스핀은 스핀 자기 모멘트를 생성하여 전자가 매우 작은 자석처럼 작용합니다. 원자들이 균질하지 않은 자기장을 통과할 때, 자기장의 힘 모멘트는 전자의 위치가 더 강한 자기장의 방향과 일치할 때까지 전자의 쌍극자에 영향을 미칩니다. 그러면 원자가 전자의 스핀 값에 따라 원자는 더 강한 자기장 쪽으로 특정한 양만큼 당겨지거나 멀어집니다. 전자의 스핀이 ++ 1/2일 때 원자는 더 강한 장에서 멀어지고, 스핀이 -+ 1/2일 때 원자는 전자 쪽으로 움직입니다. 따라서 은 원자의 빔은 각 원자가 전자의 스핀에 따라 균질하지 않은 자기장을 통과하는 동안 쪼개집니다.
1927년 핍스와 테일러는 유사한 결과를 가진 수소 원자를 사용하여 유사한 실험을 수행했습니다. 이후의 과학자들은 원자가 껍질에 단 하나의 전자만을 가지고 있는 다른 원자들을 사용하여 실험을 했습니다: (구리, 금, 나트륨, 칼륨). 매번 금속판에 두 개의 선이 형성되었습니다.
원자핵에도 스핀이 있을 수 있지만 양성자와 중성자는 전자보다 훨씬 무겁고(약 1836배), 자기쌍극자 모멘트는 질량에 반비례합니다. 그래서 핵자기쌍극자 운동량은 원자 전체의 운동량보다 훨씬 작습니다. 이 작은 자기 쌍극자는 나중에 스턴, 프리쉬, 이스터먼에 의해 측정되었습니다.
전자 상자 공명
짝을 이루지 않은 전자를 가진 원자나 분자의 경우, 전자 오비탈이나 다른 양자수의 변화 없이 스핀 양자수만 변하는 자기장의 전이도 관찰할 수 있습니다. 이것은 자유 라디칼을 연구하는 데 사용되는 전자 상자 공명(EPR) 또는 전자 스핀 공명(ESR)의 방법입니다. 스핀의 자기적 상호작용만 변하기 때문에 에너지 변화는 궤도 사이의 전이보다 훨씬 작고 스펙트럼은 마이크로파 영역에서 관찰됩니다.
스핀 벡터와의 관계
비상대론적 파울리 방정식 또는 상대론적 디랙 방정식의 해에 대해서 양자화된 각운동량은 다음과 같이 쓸 수 있습니다.
- 은(는) 양자화된 스핀 벡터 또는 스피너입니다.
- {s \Vert }이(가) 스핀 벡터의 표준입니다.
- s는 스핀 각운동량과 연관된 스핀 양자수입니다.
- \hbar}는 축소된 플랑크 상수입니다.
임의의 방향 z(일반적으로 외부 자기장에 의해 결정됨)가 주어지면 스핀 z-투영은 다음과 같이 주어집니다.
여기서 m은s 자기 스핀 양자수로서 -s부터 +s까지 1의 단계로 나뉩니다. 이렇게 하면 2초 + 1개의 다른 ms 값이 생성됩니다.
s에 허용되는 값은 음수가 아닌 정수 또는 반 정수입니다. 페르미온은 전자, 양성자, 중성자를 포함한 반 integer 값을 갖는데, 모두 s = ++ 1/2를 갖습니다. 광자와 모든 중간자와 같은 보손은 정수 스핀 값을 갖습니다.
대수
스핀에 대한 대수 이론은 양자역학 이론에서 각운동량을 탄소 복사한 것입니다.[15] 우선 스핀은 기본적인 정류 관계를 만족합니다.
다음으로 및 의 고유 벡터는 다음을 만족합니다.
디랙 방정식의 에너지 준위
1928년 폴 디랙은 상대론적 파동 방정식을 개발했는데, 지금은 디랙 방정식이라고 부르며, 스핀 자기 모멘트를 정확하게 예측함과 동시에 전자를 점 같은 입자로 취급했습니다. 수소 원자 내 전자의 에너지 준위에 대한 디랙 방정식을 풀면서 s를 포함한 네 개의 양자수는 모두 자연적으로 발생했고 실험과 잘 일치했습니다.
원자 또는 분자의 총 스핀
일부 원자의 경우 짝을 이루지 않은 여러 전자(s12, s, ...)의 스핀이 결합되어 총 스핀 양자수 S를 형성합니다.[16][17] 이것은 스핀-궤도 결합이 스핀 사이의 결합 또는 궤도 각운동량 사이의 결합에 비해 약할 때 특히 가벼운 원자(또는 가벼운 원자로만 형성된 분자)에서 발생합니다. 이 상황은 L과 S가 운동 상수이기 때문에 LS 결합으로 알려져 있습니다. 여기서 L은 총 궤도 각운동량 양자수입니다.[17]
잘 정의된 S를 갖는 원자의 경우, 상태의 다중성은 2S + 1로 정의됩니다. 이는 S ≤ L(일반적인 경우)인 경우, 주어진 (L, S) 조합에 대한 총 (궤도 + 스핀) 각운동량 J의 가능한 다른 값의 수와 같습니다. 예를 들어, S = 1인 경우, 세 개의 상태가 삼중항을 형성합니다. 이 세 가지 상태에 대한 S의 고유값은 +1 ħ, 0 및 -1 ħ입니다. 원자 상태의 용어 기호는 L, S, J의 값을 나타냅니다.
예를 들어, 산소 원자와 이산화수소 분자의 바닥 상태는 짝을 이루지 않은 두 개의 전자를 가지므로 삼중항 상태입니다. 원자 상태는 기호 P, 분자 상태는 기호 σ로 기술됩니다.
참고 항목
참고문헌
- ^ Pauling, Linus (1960). The nature of the chemical bond and the structure of molecules and crystals: an introduction to modern structural chemistry. Ithaca, N.Y. ISBN 0-8014-0333-2. OCLC 545520.
{{cite book}}: CS1 maint: 위치 누락 게시자(링크) - ^ "ISO 80000-10:2019". International Organization for Standardization. Retrieved 2019-09-15.
- ^ Atkins, Peter; de Paula, Julio (2006). Atkins' Physical Chemistry (8th ed.). W.H. Freeman. p. 308. ISBN 0-7167-8759-8.
- ^ Banwell, Colin N.; McCash, Elaine M. (1994). Fundamentals of Molecular Spectroscopy. McGraw-Hill. p. 135. ISBN 0-07-707976-0.
- ^ a b Perrino, Charles T.; Peterson, Donald L. (1989). "Another quantum number?". J. Chem. Educ. 66 (8): 623. Bibcode:1989JChEd..66..623P. doi:10.1021/ed066p623. ISSN 0021-9584.
- ^ Petrucci, Ralph H.; Harwood, William S.; Herring, F. Geoffrey (2002). General Chemistry (8th ed.). Prentice Hall. p. 333. ISBN 0-13-014329-4.
- ^ Whitten, Kenneth W.; Galley, Kenneth D.; Davis, Raymond E. (1992). General Chemistry (4th ed.). Saunders College Publishing. p. 196. ISBN 0-03-072373-6.
- ^ Karplus, Martin, 그리고 Porter, Richard Needham. 원자와 분자. 미국, W.A. Benjamin, 1970.
- ^ Halpern, Paul (2017-11-21). "Spin: The quantum property that should have been impossible". Forbes. Starts with a bang. Archived from the original on 2018-03-10. Retrieved 2018-03-10.
- ^ 만짓 쿠마르, 퀀텀: 아인슈타인, 보어와 현실의 본질에 관한 위대한 논쟁, 2008.
- ^ Langmuir, Irving (1919). "The arrangement of electrons in atoms and molecules". Journal of the Franklin Institute. 187 (3): 359–362. doi:10.1016/S0016-0032(19)91097-0.
- ^ 볼프강 파울리. 배제 원리와 양자역학. ⟨ http://nobelprize.org ⟩를 통해 온라인으로 이용할 수 있습니다. 1946년 12월 13일 노벨 물리학상 수상자 발표
- ^ Atkins, Peter; de Paula, Julio (2006). Atkins' Physical Chemistry (8th ed.). W.H. Freeman. p. 515. ISBN 0-7167-8759-8.
- ^ Cottingham, W.N.; Greenwood, D.A. (1986). An introduction to nuclear physics. Cambridge University Press. pp. 36, 57. ISBN 0-521-31960-9.
- ^ 데이비드 J. 그리피스, 양자역학 개론(책), 오리건, 리드 칼리지, 2018, 166p. ISBN 9781107189638.
- ^ a b Merzbacher, E. (1998). Quantum Mechanics (3rd ed.). John Wiley. pp. 430–431. ISBN 0-471-88702-1.
- ^ a b Atkins, P.; de Paula, J. (2006). Physical Chemistry (8th ed.). W.H. Freeman. p. 352. ISBN 0-7167-8759-8.
외부 링크
- Weiss, Michael (2001). "Full treatment of spin – including origins, evolution of spin theory, and details of the spin equations". Department of Mathematics. UC Riverside.
 두
두 













 (는) 양자화된
(는) 양자화된 
![{\displaystyle \ [S_{i},S_{j}]=i\ \hbar \ \epsilon _{ijk}\ S_{k}\ ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0a5b23972acdc47ffb28ee19015a0fc4f180d97)
![{\displaystyle \ \left[S_{i},S^{2}\right]=0\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/12f311610f445def9662755454c783f4fd0916af)







