단조 함수
Monotonic function수학에서 단조함수(또는 단조함수)는 주어진 [1][2][3]순서를 유지하거나 반대로 하는 순서 집합 사이의 함수입니다.이 개념은 미적분학에서 처음 생겨났고, 나중에 질서 이론의 더 추상적인 설정으로 일반화되었다.
미적분과 분석에서
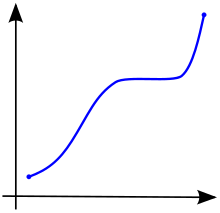
미적분학에서 실수의 서브셋에 정의되어 있는 f{ f는 완전히 증가하지 않거나 완전히 [2]감소하지 않는 경우에 한해 단조라고 불립니다.즉, 그림 1과 같이 단조롭게 증가하는 함수는 배타적으로 증가할 필요가 없으며 단순히 감소하지 않아야 한다.
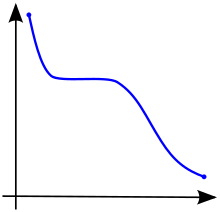
x y \ x\ yf( ) f\ f f f f f f f f f f f f f f f f {\ {\ {\ {\ {\ x ( ( f {\ {\ {\ f f f f f f f f f f f f f f f {\ {\ f f {\ {\ f f f f f f f f f f f {\ {\ f f ( x 를 갖는 경우, 함수는 단조절 증가 [3]또는 비감소라고 불립니다. 이므로 ff는 순서를 유지합니다(그림 1 참조).마찬가지로 함수는 단조로운 감소(감소 또는 비증가)[3]라고 불리며, y x \ y() \ f\ ! 이므로 순서가 반전됩니다(그림2 참조).
단조성의 정의에서 순서{\(\를 엄밀한 순서{\(\displaystyle로 대체하면 더 강력한 요건을 얻을 수 있다.이 속성을 가진 함수를 엄밀하게 증가(증가)[3][4]라고 합니다.순서 기호를 반전시키면 엄밀하게 감소(또한 감소)[3][4]라는 해당 개념을 찾을 수 있습니다.함수가 엄격하게 증가하거나 완전히 감소하는 경우 엄밀하게 단조함수라고 할 수 있습니다.엄밀하게 단조로운 함수는 일대일입니다(xx는 x x\ x가 때문에 f f f ff f
"증가"와 "감소"가 연속된 인수로 동일한 값을 반복할 가능성을 포함하는 것으로 간주되지 않는 경우, 이 가능성을 강조하기 위해 약단조, 약단조 및 약단조라는 용어를 사용할 수 있습니다.
"비감소"와 "비증가"라는 용어는 (훨씬 약한) 부정적인 조건인 "감소하지 않음"과 "증가하지 않음"과 혼동해서는 안 된다.예를 들어, 그림 3의 함수는 먼저 하강하고, 그 다음에 상승하고, 다시 하강합니다.따라서 감소하지도 증가하지도 않지만 감소하지도 않고 증가하지도 않습니다.
f { f는 의 차수의도함수가 음수가 아니거나 간격의 모든 점에서 모두 양수가 아닌 경우에 걸쳐 절대적으로 단조롭다고 합니다
역함수
단조롭지만 엄밀하게 단조롭지는 않으므로 구간에서 일정한 함수에는 역함수가 없습니다.이는 함수가 역수를 가지려면 범위에서 함수의 도메인으로의 일대일 매핑이 필요하기 때문입니다.단조 함수는 도메인 내에서 일정한 값을 가지므로 이 상수 값에 매핑되는 범위 내에 여러 개의 값이 있음을 의미합니다.
그러나 엄밀하게 단조로운 함수 y = g(x)는 x = h(y)와 같은 역함수를 가지고 있는데, 이는 함수의 범위와 영역 사이의 일대일 매핑이 항상 보장되기 때문이다.또, 함수는, 값의 범위에서는 엄격히 단조롭다고 말할 수 있기 때문에, 그 값의 범위에서는 역수를 가진다.예를 들어, y = g(x)가 범위 [a, b]에서 엄격히 단조롭다면 범위 [g(a), g(b)]에서 역x = h(y)를 갖지만 함수의 전체 범위가 역수를 갖는다고 말할 수는 없습니다.
참고: 일부[which?] 교과서는 단조 함수에 대해 역이 존재한다는 것을 의미할 때 단조 함수에 대해 역이 존재한다고 잘못 기술합니다.
단조 변환
단조 변환(또는 단조 변환)이라는 용어는 엄밀하게 증가하는 함수에 의한 변환을 의미하기 때문에 혼동을 일으킬 수도 있습니다.이는 경제학에서 단조 변환에 걸쳐 보존되는 효용 함수의 순서적 특성에 관한 경우이다(단조 [5]선호도 참조).이러한 맥락에서, 우리가 "단조 변환"이라고 부르는 것은, 보다 정확하게는 "긍정적 단조 변환"이라고 불리며,[6] 이는 숫자의 순서를 반대로 하는 "부정적 단조 변환"과 구별하기 위해서이다.
기본적인 응용 프로그램 및 결과
단조 f {\ f \ \의 성질은 참입니다.
- f는 영역의 모든 점에서 오른쪽과 왼쪽에서 제한이 있다.
- f{\ f에는 실수 「\} 또는 - 의 양수 또는 음수 무한대 {\\infty의 제한이 있습니다.
- f는 점프 불연속만 가질 수 있다.
- f는 도메인 내에서 셀 수 없을 정도로 많은 불연속성을 가질 수 있습니다.단, 불연속부는 반드시 고립점으로 구성되는 것은 아니며 간격(a, b)에서 밀도가 높을 수도 있다.예를 들어, 양의 임의의 가산}) 및 유리수의( i {에 대해 단조 증가 함수.모든 비합리적인 숫자에 정확히 연속됩니다(그림 참조).이는 유리수에 대한 이산 측정치의 누적 분포 함수이며 서 i(\})는 {의 가중치입니다.
이러한 특성 때문에 단조로운 함수가 분석의 기술적 작업에 유용한 것입니다.이러한 기능에 관한 몇 가지 추가 정보는 다음과 같습니다.
- f{\f가 간격I에 정의된 단조 인 f {\는 I의 거의 모든 곳에서 구별됩니다. 즉 I {\ I의 집합x {\ 는 f {\ f와 구별되지 .의{\ x에는 르베그 측정값이 0입니다.또한 이 결과는 카운트 가능 상태로 개선할 수 없습니다. 칸토어 기능을 참조하십시오.
- 이 세트가 계산 가능한 경우 f는 절대적으로 연속적입니다.
- f{\ f가 간격 b {에서 정의된 단조 함수인 f {\ f는 Riemann 적분 가능합니다.
단조 함수의 중요한 적용은 확률론이다.X X가 랜덤 변수인 ) Prob( x \ \ x는 단조롭게 증가하는 함수입니다
어떤 점(모드)까지 단조롭게 증가하다가 단조롭게 감소하는 함수는 단조로운 것입니다.
f f가 엄밀하게 단조로운 함수일 ff}는 그 영역에 주입되며 T{ T가 ff의 범위일 T{ t에서는 f에 역함수가 존재하며, 반대로 각 상수함수는 단조이다.주사는 [7]아니므로 역수를 가질 수 없습니다.
토폴로지 내
f : (\ fY )는 각각의 파이버가 연결되어 있는 경우 모노톤이라고 합니다.즉, 각 yY에 대해 (\ Y f - ( y )\ f는의 연결된 서브스페이스입니다
기능 분석 중
위상 벡터 의 함수 해석에서 a(비선형 T : X { \ : X \ X { * }}는 다음과 같은 경우 단조 연산자라고 한다.
Kachurovskii의 정리는 바나흐 공간의 볼록함수가 그 도함수로서 단조 연산자를 갖는다는 것을 보여준다.
× 의G(\ G는 Gdisplaystyle [및[22 Gdisplaystyle G\displaystyle X X^{*})의 모든에 대해 모노톤 집합이라고 합니다.
G는 집합포함이라는 의미에서 모든 단조 집합 중 최대일 경우 최대 단조라고 한다.모노톤 G () \ G ( )그래프는 모노톤 집합입니다.단조 연산자는 그 그래프가 최대 단조 집합일 경우 최대 단조라고 한다.
순서론
순서론은 임의의 부분 순서 집합과 사전 순서 집합을 실수의 일반화로서 다룬다.위의 단조성의 정의는 이러한 경우에도 관련이 있다.단, "증가"와 "감소"라는 용어는 사용하지 않습니다. 왜냐하면 기존의 그림 표현은 전체 주문에 적용되지 않기 때문입니다.게다가 엄격한 관계<와 >는, 많은 비합계 주문에서는 거의 도움이 되지 않기 때문에, 그 외의 용어는 도입되지 않습니다.
θ는 부분 순서 집합의 부분 순서 관계를 나타내며, 아이소톤이라고도 불리는 단조 함수는 이 특성을 만족한다.
- x y y는 f(x) ≤ f(y)를 의미합니다.
도메인 내의 모든 x 및 y에 대해.두 개의 단조 매핑의 합성도 단조입니다.
이중 개념은 종종 안티톤, 안티 모노톤 또는 순서 반전이라고 불립니다.따라서 안티톤 함수 f는 다음 특성을 만족한다.
- x y y는 f(y) ≤ f(x)를 의미합니다.
도메인 내의 모든 x 및 y에 대해.
상수 함수는 단조 함수와 반음 함수가 모두이며, 반대로 f가 단조 함수와 반음이고 f의 영역이 격자인 경우에는 f가 일정해야 합니다.
단조 함수는 순서 이론의 중심이다.그것들은 그 주제에 관한 대부분의 기사에 나타나며, 특별한 적용 사례들은 이러한 곳에서 볼 수 있다.주목할 만한 특별한 단조 함수는 순서 임베딩(f(x) f f(y)일 경우에만 x ≤ y가 되는 함수)과 순서 동형(주사적 순서 임베딩)이다.
검색 알고리즘의 맥락에서
검색 알고리즘의 맥락에서 단조성(일명 일관성)은 경험적 함수에 적용되는 조건입니다.경험적 h(n)는 모든 노드 n과 작용 a에 의해 생성된 모든 n의 후속 n'에 대해 n'에서 목표에 도달하는 추정비용이 n'까지의 단계비용과 n'에서 목표에 도달하는 추정비용보다 크지 않다면 단조롭다.
이것은 n, n'과 목표n G가 n에 가장 가까운 삼각 부등식의 한 형태이다.모든 단조 경험적 접근법도 허용 가능하기 때문에 허용 가능성보다 단조성이 더 엄격한 요구 사항입니다.A*와 같은 일부 휴리스틱 알고리즘은 사용하는 휴리스틱이 [8]단조롭다면 최적임을 증명할 수 있다.
Boolean 함수에서
부울대수에서 단조함수는 {0,1}의 모든i a와i b에 대해 a11 b2, a2 b, …, an in bn(즉, 데카르트곱 {0, n1)가 좌표방향으로 정렬되어 있으면 f1(a, ..., a) ( f1(bn, ..., b)가 되는 함수이다.즉, 모든 입력 조합에 대해 입력 중 하나를 false에서 true로 전환하면 출력이 false에서 true로 전환되고 true에서 false로 전환되지 않을 수 있는 경우 부울 함수는 단조롭습니다.그래픽으로 볼 때, 이는 n-ary 부울 함수가 true에서 false로 라벨링된 n-cube로 표현될 때 단조롭다는 것을 의미합니다.(이 라벨이 붙은 하세 다이어그램은 함수의 라벨이 붙은 벤 다이어그램의 쌍대이며, 이는 n † 3에 대한 보다 일반적인 표현이다.)
단조로운 부울 함수는 연산자 및 또는 (특히 금지되지 않음)만 사용하여 입력(복수 이상 나타날 수 있음)을 조합하는 식에 의해 정확하게 정의될 수 있는 함수입니다.예를 들어 "a, b, c 홀드"는 (a 및 b), (a 및 c) 또는 (b 및 c)로 쓸 수 있기 때문에 a, b, c의 단조함수이다.
n개의 변수에 대한 이러한 함수의 수를 n의 데데킨드 수라고 합니다.
「 」를 참조해 주세요.
- 단조 입방 보간법
- 의사 모노톤 연산자
- Spearman의 순위 상관 계수 - 데이터 집합의 단조성을 측정합니다.
- 총단조성
- 순환 단조성
- 연산자 단조 함수
메모들
- ^ Clapham, Christopher; Nicholson, James (2014). Oxford Concise Dictionary of Mathematics (5th ed.). Oxford University Press.
- ^ a b Stover, Christopher. "Monotonic Function". Wolfram MathWorld. Retrieved 2018-01-29.
- ^ a b c d e "Monotone function". Encyclopedia of Mathematics. Retrieved 2018-01-29.
- ^ a b Spivak, Michael (1994). Calculus. 1572 West Gray, #377 Houston, Texas 77019: Publish or Perish, Inc. p. 192. ISBN 0-914098-89-6.
{{cite book}}: CS1 유지보수: 위치(링크) - ^ Simon & Blume(1994)의 카디널 대 서수 유틸리티 섹션을 참조하십시오.
- ^ Varian, Hal R. (2010). Intermediate Microeconomics (8th ed.). W. W. Norton & Company. p. 56. ISBN 9780393934243.
- ^ 도메인에 여러 요소가 있는 경우
- ^ 최적화를 위한 조건:수용성과 일관성(94-95페이지) (Russell & Norvig 2010).
참고 문헌
- Bartle, Robert G. (1976). The elements of real analysis (second ed.).
- Grätzer, George (1971). Lattice theory: first concepts and distributive lattices. ISBN 0-7167-0442-0.
- Pemberton, Malcolm; Rau, Nicholas (2001). Mathematics for economists: an introductory textbook. Manchester University Press. ISBN 0-7190-3341-1.
- Renardy, Michael & Rogers, Robert C. (2004). An introduction to partial differential equations. Texts in Applied Mathematics 13 (Second ed.). New York: Springer-Verlag. p. 356. ISBN 0-387-00444-0.
- Riesz, Frigyes & Béla Szőkefalvi-Nagy (1990). Functional Analysis. Courier Dover Publications. ISBN 978-0-486-66289-3.
- Russell, Stuart J.; Norvig, Peter (2010). Artificial Intelligence: A Modern Approach (3rd ed.). Upper Saddle River, New Jersey: Prentice Hall. ISBN 978-0-13-604259-4.
- Simon, Carl P.; Blume, Lawrence (April 1994). Mathematics for Economists (first ed.). ISBN 978-0-393-95733-4. (정의 9.31)
외부 링크
- "Monotone function", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Anik Debnath와 Thomas Roxlo(The Harker School), Wolfram 시연 프로젝트의 단조로운 시퀀스의 융합.
- Weisstein, Eric W. "Monotonic Function". MathWorld.

 완전히 증가하지 않거나 완전히
완전히 증가하지 않거나 완전히 



 엄밀한 순서
엄밀한 순서







 걸쳐 절대적으로 단조롭다고 합니다
걸쳐 절대적으로 단조롭다고 합니다





 대해 단조 증가 함수.
대해 단조 증가 함수.



![\left[a, b\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/f30926fb280a9fdf66fd931e14d4363cb824feaa)

 단조롭게 증가하는 함수입니다
단조롭게 증가하는 함수입니다 f
f




 G
G![{\displaystyle [u_{1},w_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42f2c67bc4887974d491ba4a419dc798ed50d8cd)

![{\displaystyle [u_{2},w_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32202d66739c2039a8b74e861330c713a44db704) 모든
모든






