검색 알고리즘
Search algorithm컴퓨터 과학에서, 검색 알고리즘은 검색 문제를 해결하는 알고리즘이다.검색 알고리즘은 일부 데이터 구조 내에 저장되거나 문제 도메인의 검색 공간에 계산된 정보를 이산형 또는 연속형 값으로 검색하는 작업을 한다.
위에서 설명한 검색 문제와 웹 검색 모두 정보 검색의 문제지만, 일반적으로 별도의 하위 분야로 연구되어 해결과 평가가 다르게 이루어진다.웹 검색 문제는 일반적으로 인간 질의와 가장 관련성이 높은 문서를 필터링하고 찾는 데 초점이 맞춰져 있다.고전적인 검색 알고리즘은 일반적으로 그들이 얼마나 빨리 해결책을 찾을 수 있는지, 그리고 그 솔루션이 최적의 솔루션인지에 대해 평가된다.정보 검색 알고리즘은 빨라야 하지만, 순위의 질, 좋은 결과가 빠지고 나쁜 결과가 포함됐는지 여부가 더 중요하다.
적절한 검색 알고리즘은 종종 검색되는 데이터 구조에 따라 달라지며 데이터에 대한 사전 지식을 포함할 수도 있다.검색 알고리즘은 검색 트리, 해시 맵, 데이터베이스 인덱스 등 특수하게 구성된 데이터베이스 구조를 통해 더 빠르고 효율적으로 만들 수 있다.[2][full citation needed][3]
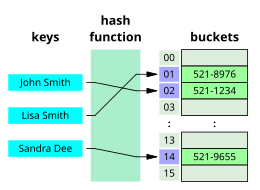
검색 알고리즘은 검색 메커니즘을 기반으로 선형, 이진, 해싱의 세 가지 유형의 알고리즘으로 분류할 수 있다.선형 검색 알고리즘은 대상 키와 연관된 모든 레코드를 선형 방식으로 검사한다.[4]바이너리, 즉 반간격 검색은 반복적으로 검색 구조의 중심을 겨냥하여 검색 공간을 반으로 나눈다.비교 검색 알고리즘은 대상 기록이 발견될 때까지 키의 비교에 기초한 기록을 연속적으로 제거함으로써 선형 검색 시 개선되며, 정해진 순서에 따라 데이터 구조에 적용할 수 있다.[5]디지털 검색 알고리즘은 숫자 키를 사용하는 데이터 구조에서 자릿수 속성을 기반으로 작동한다.[6]마지막으로 해싱은 해시함수를 기반으로 키를 레코드에 직접 매핑한다.[7]
알고리즘은 종종 계산 복잡성 또는 최대 이론적 실행 시간으로 평가된다.예를 들어 바이너리 검색 함수는 최대 복잡도가 O(log n) 또는 로그 시간이다.이는 검색 대상을 찾는 데 필요한 최대 작업 수가 검색 공간 크기의 로그 함수라는 것을 의미한다.
검색 알고리즘의 적용
검색 알고리즘의 특정 적용 분야는 다음과 같다.
- 조합 최적화의 문제(예:
- 최단 경로 문제의 한 형태인 차량 경로 문제
- 배낭 문제:각각 가중치와 값이 있는 항목 집합을 지정하면 총 가중치가 지정된 한계보다 작거나 같으며 총 값이 가능한 한 커지도록 집합에 포함할 각 항목의 수를 결정한다.
- 간호사 스케줄링 문제
- 제약 조건 만족도 문제:
- 게임 이론과 특히 결합 게임 이론에서, 다음으로 가장 잘 할 수 있는 동작을 선택한다(예: minmax 알고리즘)
- 전체 가능성 집합에서 조합 또는 비밀번호 찾기
- 정수 인수(암호화에서 중요한 문제)
- 공정의 매개변수(온도, 압력, pH 등)를 변경하여 화학적 반응과 같은 산업적 공정 최적화
- 데이터베이스에서 레코드 검색
- 목록 또는 배열에서 최대 또는 최소 값 찾기
- 지정된 값이 값 집합에 있는지 확인하는 중
반
가상 검색 공간의 경우
가상 공간 검색을 위한 알고리즘은 제약조건 만족도 문제에 사용되는데, 여기서 목적은 특정 수학 방정식과 불평등/평등을 만족시킬 특정 변수에 대한 일련의 가치 할당을 찾는 것이다.또한 그러한 변수들의 특정 함수를 최대화하거나 최소화하는 변수 할당을 찾는 것이 목표일 때 사용된다.이러한 문제들에 대한 알고리즘에는 기본적인 무차별적인 검색("naute-force search" 또는 "무정보" 검색이라고도 함)과 선형 이완, 구속조건 생성, 구속조건 전파와 같이 이 공간의 구조에 대한 부분적인 지식을 이용하려고 하는 다양한 경험적 접근법이 포함된다.
중요한 하위 클래스는 검색 공간의 요소를 그래프의 정점으로 보고, 사례에 적용되는 일련의 경험적 접근에 의해 정의된 가장자리를 가지고, 예를 들어 가장 가파른 내리막이나 가장 먼저의 기준에 따라 가장자리를 따라 항목 간에 이동하거나 확률적인 검색으로 공간을 스캔하는 로컬 검색 방법이다.이 범주에는 특정 방식으로 임의의 발견을 결합한 시뮬레이션 어닐링, 타부 검색, A-팀 및 유전자 프로그래밍과 같은 매우 다양한 일반적인 메타휴리스틱 방법이 포함된다.현지 검색과 정반대되는 것은 글로벌 검색 방식이 될 것이다.이 방법은 검색공간이 제한되지 않고 주어진 네트워크의 모든 측면을 검색 알고리즘을 실행하는 기업이 이용할 수 있는 경우에 적용할 수 있다.[8]
이 세분류는 또한 다양한 트리 검색 알고리즘을 포함하며, 이 알고리즘은 요소를 트리의 정점으로 보고 특정 순서로 트리를 가로지른다.후자의 예로는 깊이 우선 검색, 너비 우선 검색 등 철저한 방법과 백트랙팅, 분기 및 바인딩 등 다양한 휴리스틱 기반 검색 트리 가지치기 방법을 들 수 있다.기껏해야 확률론적 의미에서만 작용하는 일반적인 메타휴리스틱스와는 달리, 이러한 트리 검색 방법의 상당수는 충분한 시간이 주어진다면 정확하거나 최적의 해결책을 찾을 수 있도록 보장된다.이것은 "완전성"이라고 불린다.
또 다른 중요한 하위 클래스는 체스나 백개먼과 같은 다중 플레이어 게임의 게임 트리를 탐색하기 위한 알고리즘으로 구성되며, 노드는 현재 상황에서 발생할 수 있는 모든 가능한 게임 상황으로 구성된다.이러한 문제에서 목표는 상대의 가능한 모든 움직임을 고려하여 최고의 승기를 제공하는 움직임을 찾는 것이다.유사한 문제는 로봇 지침이나 마케팅, 금융 또는 군사 전략 계획과 같이 결과가 전적으로 자신의 통제 하에 있지 않은 연속적인 결정을 내려야 할 때 발생한다.이런 종류의 문제, 즉 결합 검색은 인공지능의 맥락에서 광범위하게 연구되어 왔다.이 세분류에 대한 알고리즘의 예로는 미니맥스 알고리즘, 알파-베타 프루닝, A* 알고리즘과 그 변형 등이 있다.
특정 구조물의 하부 구조용
"결합 검색"이라는 이름은 일반적으로 그래프, 문자열, 유한 그룹 등 주어진 이산 구조의 특정 하위 구조를 찾는 알고리즘에 사용된다.조합 최적화라는 용어는 일반적으로 어떤 매개변수의 최대(또는 최소) 값을 가진 하부 구조를 찾는 것이 목표일 때 사용된다.(하위 구조는 대개 제약조건이 있는 정수변수의 집합에 의해 컴퓨터에 나타나기 때문에 이러한 문제는 제약조건 만족도나 이산적 opp의 특별한 경우로 볼 수 있다.시간화; 그러나 그것들은 일반적으로 내부 표현이 명시적으로 언급되지 않는 보다 추상적인 환경에서 공식화되고 해결된다.)
중요하고 광범위하게 연구된 하위 클래스는 특정 그래프(예: 서브그래프, 경로, 회로 등)에서 특정 하위 구조를 찾기 위한 그래프 알고리즘, 특히 그래프 통과 알고리즘이다.예를 들면 Dijkstra의 알고리즘, Kruskal의 알고리즘, 가장 가까운 이웃 알고리즘, Prim의 알고리즘 등이 있다.
이 범주의 또 다른 중요한 하위 클래스는 문자열 내의 패턴을 검색하는 문자열 검색 알고리즘이다.두 가지 유명한 예는 보이어-모어 및 크누스-모리스-프라트 알고리즘과 접미사 트리 데이터 구조를 기반으로 한 몇 개의 알고리즘이다.
함수의 최대값 검색
1953년 미국의 통계학자 잭 키퍼는 피보나치 검색을 고안했는데, 피보나치 검색은 단일 함수의 최대치를 찾는 데 사용될 수 있고, 컴퓨터 과학에 다른 많은 응용 프로그램을 가지고 있다.
양자 컴퓨터의 경우
데이터 구조나 휴리스틱스의 도움 없이도 이론적으로 선형이나 짐승 같은 힘 검색보다 빠른 양자컴퓨터를 위해 설계된 검색 방법도 있다.양자컴퓨터의 이면에 있는 아이디어와 애플리케이션은 여전히 완전히 이론적인 것이지만, 양자컴퓨팅 시스템의 가상적인 물리적 버전을 정확하게 복제하는 그로버와 같은 알고리즘으로 연구가 진행되어 왔다.[9]
검색 엔진 최적화
구글과 같은 검색 엔진에서 사용되는 검색 알고리즘은 수많은 중요 요인을 기준으로 관련 검색 결과를 주문한다.[10]검색 엔진 최적화(SEO)는 검색 알고리즘과 연계하여 주어진 검색 결과가 검색 알고리즘과 함께 작동하여 해당 사이트에 대한 더 많은 트랙션, 주의 및 클릭을 유기적으로 획득하는 과정이다.이는 검색 엔진 알고리즘을 조정해 특정 검색 결과를 보다 비중 있게 선호하려 할 수 있지만, SEO를 중심으로 한 전략은 믿을 수 없을 정도로 중요하고 비즈니스 세계와 관련이 깊어졌다.[10]
참고 항목
- 후진 유도
- 컨텐츠 주소 지정 메모리 – 특정 초고속 검색 애플리케이션 하드웨어에 사용되는 특수한 유형의 컴퓨터 메모리
- 2상 진화 – 복잡한 적응형 시스템 내에서 자체 조직을 추진하는 프로세스
- 선형검색문제
- 검색 및 최적화에 무료 점심식사 없음 – 평균 솔루션 비용은 모든 방법과 동일함
- 추천자 시스템 – 사용자의 선호도를 예측하는 정보 필터링 시스템, 또한 통계적 방법을 사용하여 매우 큰 데이터 세트의 결과 순위를 매긴다.
- 검색엔진(컴퓨터)
- 검색 게임 – 2인용 제로섬 게임
- 선택 알고리즘 – 목록 또는 배열에서 k번째 가장 작은 숫자를 찾기 위한 알고리즘
- 해결사 – 일련의 수학 문제를 위한 소프트웨어
- 정렬 알고리즘 – 특정 검색 알고리즘 실행에 필요한 목록을 순서대로 정렬하는 알고리즘
- 웹 검색 엔진
카테고리:
참조
인용구
- ^ Davies, Dave (May 25, 2020). "How Search Engine Algorithms Work: Everything You Need to Know". Search Engine Journal. Retrieved 27 March 2021.
{{cite web}}: CS1 maint : url-status (링크) - ^ Beame & Fich 2002, 페이지 39.
- ^ Knuth 1998, §6.5("보조 키에 대한 회수").
- ^ Knuth 1998, §6.1("시퀀셜 검색"). 없음:
- ^ Knuth 1998, §6.2("키 비교에 의한 검색").
- ^ Knuth 1998, §6.3(디지털 검색).
- ^ 크누스 1998, §6.4, (해싱)
- ^ Hunter, A.H.; Pippenger, Nicholas (4 July 2013). "Local versus global search in channel graphs". Networks: An International Journey. arXiv:1004.2526.
- ^ López, G V; Gorin, T; Lara, L (26 February 2008). "Simulation of Grover's quantum search algorithm in an Ising-nuclear-spin-chain quantum computer with first- and second-nearest-neighbour couplings". Journal of Physics B: Atomic, Molecular and Optical Physics. 41 (5): 055504. arXiv:0710.3196. Bibcode:2008JPhB...41e5504L. doi:10.1088/0953-4075/41/5/055504. S2CID 18796310.
- ^ a b Baye, Michael; De los Santos, Barbur; Wildenbeest, Matthijs (2016). "Search Engine Optimization: What Drives Organic Traffic to Retail Sites?". Journal of Economics & Management Strategy. 25: 6–31. doi:10.1111/jems.12141. S2CID 156960693.
참고 문헌 목록
책들
- Knuth, Donald (1998). Sorting and Searching. The Art of Computer Programming. Vol. 3 (2nd ed.). Reading, MA: Addison-Wesley Professional.
기사들
- Schmittou, Thomas; Schmittou, Faith E. (2002-08-01). "Optimal Bounds for the Predecessor Problem and Related Problems". Journal of Computer and System Sciences. 65 (1): 38–72. doi:10.1006/jcss.2002.1822.