오일러 토션 함수

수론에서 오일러의 토션 함수는 상대적으로 소수인 주어진 정수 n까지 양의 정수를 세는 것입니다. 그리스 문자 파이를$$φ(n) ${\displaystyle \varphi$($n{\displaystyle )\}\mathrm{또는}}$ϕ(n)${\displaystyle$\phi(n)}로 표기하며 오일러의 파이 함수라고도 할 수 있습니다. 즉, 최대 공약수 gcd(n, k)가 1과 같은 1≤k≤n 범위의 정수 k의 개수입니다.^[2][3] 이 형태의 정수 k는 때때로 n의 토털레이션이라고 불립니다.

예를 들어, n = 9의 토털은 6개의 숫자 1, 2, 4, 5, 7, 8입니다. 이들은 모두 9로 비교적 소수이지만, 이 범위에 있는 다른 세 숫자인 3, 6, 9는 gcd(9, 3) = gcd(9, 6) = 3 및 gcd(9, 9) = 9이기 때문에 그렇지 않습니다. 따라서, φ(9) = 6. 다른 예로서, n = 1에 대하여 1부터 n까지의 범위에 있는 유일한 정수는 1 그 자체이고, gcd(1, 1) = 1이기 때문에 φ(1) = 1.

오일러의 토션 함수는 곱셈 함수로, 두 수 m과 n이 상대적으로 소수이면 φ(mn) = φ(mn) φ(n)임을 의미합니다. 이 함수는 정수 모듈론의 곱셈 그룹($고리{\displaystyle \mathbb{}}$ Z${\displaystyle }$/ ${\displaystyle n\mathbb{}}$ ${\displaystyle Z}$ ${\$의 단위 그룹)의 순서를 제공합니다.$$^[6] 또한 RSA 암호화 시스템을 정의하는 데 사용됩니다.

역사, 용어 및 표기법

레온하르트 오일러는 1763년에 이 함수를 도입했습니다.^[7][8][9] 그러나 그 당시에 그는 그것을 나타내기 위해 어떤 특정한 기호를 선택하지 않았습니다. 1784년 출판물에서 오일러는 이 함수를 더 연구하여 그리스 문자 π를 사용하여 이를 나타내는 π D를 썼습니다. 이 정의는 D = 1에서 토텐셜 함수에 대한 현재 정의와는 다르지만 그렇지 않은 경우에도 동일합니다. 현재 표준 표기법인 φ(A)는 가우스의 1801년 논문 디스퀴지션스 산술(Disquisitiones Armeticae)에서 유래했지만, 가우스는 논쟁 주변에서 괄호를 사용하지 않았고 φ A를 작성했습니다. 따라서 오일러의 파이 함수 또는 간단히 파이 함수라고 하는 경우가 많습니다.

1879년 J. J. 실베스터는 이 함수에 대한 토텐트라는 용어를 만들어냈고,^[14][15] 따라서 오일러 토텐트 함수, 오일러 토텐트 또는 오일러 토텐트라고도 합니다. 조던의 토션은 오일러의 토션을 일반화한 것입니다.

n의 동반위수는 n - φ(n)로 정의됩니다. n과 공통적으로 하나 이상의 소인수를 갖는 n보다 작거나 같은 양의 정수의 수를 세는 것입니다.

오일러 토션 함수 계산

φ(n)을 계산하는 공식에는 여러 가지가 있습니다.

오일러 곱 공식

다음과 같습니다.

${\displaystyle \varphi(n)=n\prod _{p\mid n}\left(1-{\frac {1}{p}}\right),}$

여기서 곱은 n을 나누는 서로 다른 소수 위에 있습니다. (기호에 대해서는 산술 함수를 참조하십시오.)

이와 동등한 공식은 다음과 같습니다.

where ${\displaystyle n=p_{1}^{k_{1}}p_{2}^{k_{2}}\cdots p_{r}^{k_{r}}}$ is the prime factorization of ${\displaystyle n}$ (that is, ${\displaystyle p_{1},p_{2},\ldots ,p_{r}}$ are distinct prime numbers).

이 공식들의 증명은 두 가지 중요한 사실에 달려 있습니다.

Phi는 곱셈 함수입니다.

This means that if gcd(m, n) = 1, then φ(m) φ(n) = φ(mn). 증명 개요: A, B, C를 각각 m, n, m보다 작은 양의 정수의 집합이라 하고, 따라서 A = φ(m) 등이 되도록 합니다. 그러면 중국 나머지 정리에 의해 A × B와 C 사이에 이항이 있습니다.

prime power 인수에 대한 phi 값

p가 소수이고 k가 ≥ 1이면

${\displaystyle \varphi \left(p^{k}\right)=p^{k}-p^{k-1}=p^{k-1}(p-1)=p^{k}\left(1-{\tfrac {1}{p}}\right).}$

증명: p는 소수이므로 gcd(p, m)의 유일한 가능한 값은 1, p, p, ..., p이며, gcd(p, m) > 1을 갖는 유일한 방법은 m이 p의 배수, 즉 m ∈ {p, 2p, 3p, ..., pp = p}이고 p보다 크지 않은 배수가 존재하는 경우입니다. 따라서 다른 p-p^{kk − 1} 숫자들은 모두 상대적으로 최상위^k 소수입니다.

오일러 곱 공식의 증명

산술의 기본 정리는 n > 1일 때 고유 $표현식$ n = p ${\displaystyle 1_{}^{}}$ ${\displaystyle {}_{}^{}}$ ${\displaystyle {1_{}}_{}^{}}$ ${\displaystyle {{}_{}}_{}^{}}$ 2 ${\displaystyle {}_{}^{}}$ ${\displaystyle {2_{}}_{}^{}}$ ⋯${\displaystyle {{}_{}}_{}^{}}$p$$r, ${\display$ n=p_{1}^{k_{1}} p_{2}^{k_{2}}\cdots p_{r}^{k_{r}}, 여기서 p < p < ... < p는 소수이고 각 k개의 ≥은 1입니다. (case n = 1은 빈 곱에 해당합니다.) φ의 곱셈 성질과 φ(p)에 대한 공식을 반복적으로 사용하면 다음과 같습니다.

${\displaystyle {\begin{array}{rcl}\varphi (n)&=&\varphi (p_{1}^{k_{1}})\,\varphi (p_{2}^{k_{2}})\cdots \varphi (p_{r}^{k_{r}})\\[.1em]&=&p_{1}^{k_{1}}\left(1-{\frac {1}{p_{1}}}\right)p_{2}^{k_{2}}\left(1-{\frac {1}{p_{2}}}\right)\cdots p_{r}^{k_{r}}\left(1-{\frac {1}{p_{r}}}\right)\\[.1em]&=&p_{1}^{k_{1}}p_{2}^{k_{2}}\cdots p_{r}^{k_{r}}\left(1-{\frac {1}{p_{1}}}\right)\left(1-{\frac {1}{p_{2}}}\right)\cdots \left(1-{\frac {1}{p_{r}}}\right)\\[.1em]&=&n\left(1-{\frac {1}{p_{1}}}\right)\left(1-{\frac {1}{p_{2}}}\right)\cdots \left(1-{\frac {1}{p_{r}}}\right).\end{array}}}$

이것은 오일러 곱 공식의 두 가지 버전을 모두 제공합니다.

곱셈 속성을 필요로 하지 않는 대신 소수 나눗셈으로 나눌 수 있는 정수 집합을$$제외한 ${\displaystyle \mathrm{집합}}{\displaystyle }${${\displaystyle 1,}$ 2${\displaystyle ,\dots ,}$ n${\displaystyle \}}$ ${\displaystyle \{1, 2,\ldots,n\}$에 적용된 포함 제외 원칙을 사용합니다.

예

${\displaystyle \varphi (20)=\varphi (2^{2}5)=20\,(1-{\tfrac {1}{2}})\,(1-{\tfrac {1}{5}})=20\cdot {\tfrac {1}{2}}\cdot {\tfrac {4}{5}}=8.}$

즉, 20의 서로 다른 소인수는 2와 5이고, 1부터 20까지의 20개 정수 중 절반은 2로 분할되고, 10은 남으며, 그 중 5분의 1은 5로 분할되고, 8개의 수는 20으로 동소수가 됩니다. 1, 3, 7, 9, 11, 13, 17, 19입니다.

대체 공식은 정수만 사용합니다.

푸리에 변환

토텐트는 1에서 평가된 gcd의 이산 푸리에 변환입니다.^[16] 허락하다

${\displaystyle {\mathcal {F}\{\mathbf {x} \}[m]=\sum \limits _{k=1}^{n}x_{k}\cdot e^{-2\pii}{\frac {mk}{n}}}$

where x_k = gcd(k,n) for k ∈ {1, ..., n}. 그리고나서

${\displaystyle \varphi (n)={\mathcal {F}}\{\mathbf {x} \}[1]=\sum \limits _{k=1}^{n}\gcd(k,n)e^{-2\pi i{\frac {k}{n}}}.}$

이 공식의 진짜 부분은

${\displaystyle \varphi(n)=\sum \limits _{k=1}^{n}\gcd(k,n)\cos {\tfrac {2\pik}{n}}$

예를 들어 ${\displaystyle \cos }$⁡ π ${\displaystyle \frac{}{}}$ = 5$$+ 14 {\$displaystyle \cos {\tfrac${\$pi$}{$5}}$=${\tfrac {\sqrt {5$}+1}{4}$}}}$${\displaystyle \frac{}{}}$ cos $⁡$ 2 $π$ ${\displaystyle \frac{5}{}}$ $=$ 5 - 14${\displaystyle \cos${\tfrac {2\pi}{$5}}$$=$${\tfrac {\$sqrt $5$}-1}{4}}:

오일러 곱과 약수 합 공식과는 달리 이 공식은 n의 인자를 알 필요가 없습니다. 그러나 n의 최대 공약수와 n보다 작은 모든 양의 정수의 계산이 포함되며, 이는 어쨌든 인수분해를 제공하기에 충분합니다.

약수합

가우스가 설정한 ^[17]재산은

${\displaystyle \sum _{d\mid n}\varphi(d)=n,}$

합이 n의 모든 양의 약수에 걸쳐 있는 경우, 여러 가지 방법으로 증명할 수 있습니다. (공표 규약은 산술 함수를 참조하십시오.)

한 가지 증명은 φ (d)가 고리형 그룹 C의 가능한 생성기의 수와 같다는 것입니다; 구체적으로, C = ⟨ g가 g = 1인 경우, g는 모든 k coprime에서 d에 대한 생성기입니다. C의 모든 원소는 순환 부분군을 생성하고, 모든 부분군 C ⊆ C는 C의 정확히 φ(d) 원소에 의해 생성되므로 공식은 다음과 같습니다. 마찬가지로, 이 공식은 n번째 단일근과 원시적인 d번째 단일근의 곱셈군에 적용되는 동일한 인수에 의해 유도될 수 있습니다.

이 공식은 기본 산술에서도 도출할 수 있습니다.^[19] 예를 들어, n = 20이라고 하고 분모 20과 함께 1까지의 양의 분수를 생각해 보자.

${\displaystyle {\tfrac {1}{20}},\,{\tfrac {2}{20}},\,{\tfrac {3}{20}},\,{\tfrac {4}{20}},\,{\tfrac {5}{20}},\,{\tfrac {6}{20}},\,{\tfrac {7}{20}},\,{\tfrac {8}{20}},\,{\tfrac {9}{20}},\,{\tfrac {10}{20}},\,{\tfrac {11}{20}},\,{\tfrac {12}{20}},\,{\tfrac {13}{20}},\,{\tfrac {14}{20}},\,{\tfrac {15}{20}},\,{\tfrac {16}{20}},\,{\tfrac {17}{20}},\,{\tfrac {18}{20}},\,{\tfrac {19}{20}},\,{\tfrac {20}{20}}.}$

그들을 가장 낮은 항에 넣습니다.

${\displaystyle {\tfrac {1}{20}},\,{\tfrac {1}{10}},\,{\tfrac {3}{20}},\,{\tfrac {1}{5}},\,{\tfrac {1}{4}},\,{\tfrac {3}{10}},\,{\tfrac {7}{20}},\,{\tfrac {2}{5}},\,{\tfrac {9}{20}},\,{\tfrac {1}{2}},\,{\tfrac {11}{20}},\,{\tfrac {3}{5}},\,{\tfrac {13}{20}},\,{\tfrac {7}{10}},\,{\tfrac {3}{4}},\,{\tfrac {4}{5}},\,{\tfrac {17}{20}},\,{\tfrac {9}{10}},\,{\tfrac {19}{20}},\,{\tfrac {1}{1}}}$

이 20개의 분수는 모두 양수입니다. 분모가 d = 1, 2, 4, 5, 10, 20인 k/d ≤ 1. 20을 분모로 하는 분수는 1/20, 3/20, 7/20, 9/20, 11/20, 13/20, 17/20, 19/20 등과 같이 분자가 20보다 상대적으로 소수인 분수입니다. 정의에 따라 이것은 φ(20) 분수입니다. 마찬가지로 분모가 10인 φ(10) 분수, 분모가 5인 φ(5) 분수 등이 있습니다. 따라서 20개의 분수 집합은 각 d 나눗셈 20에 대해 크기 φ(d)의 부분 집합으로 나뉩니다. 임의의 n에 대해서도 유사한 인수가 적용됩니다.

다음과 같은 약수 합 공식에 적용되는 뫼비우스 반전

${\displaystyle \varphi(n)=\sum _{d\mid n}\mu \left(d\right)\cdot {\frac {n}{d}=n\sum _{d\mid n}{\frac {\mu(d)}{d}},}$

여기서 μ는 뫼비우스 함수이며, 각 소수 p 및 k ≥ 2에 대해 $\mu {\displaystyle (\mathrm{p})}$ =${\displaystyle }$- 1 ${\displaystyle \mu(p$)=-$1}$ 및 $\mu {\displaystyle ({pk}^{}}$ = ${\displaystyle 0}$ ${\displaystyle \mu(p^{k$})=$0}$로 정의된 곱셈 함수입니다. 이 공식은 $\frac{}{}$ ∏ $p$ ∣ n (1 - $1p) {\textstyle \prod$_{$p\mid n}($1-{\frac {1$\}\{\underset{}{p\}\})}$을 곱하여$\frac{}{}$∑$$d ∣$n$μ (d$) d$. ${\textstyle \sum$_{d\mid n}{\frac {\mu(d)}{d}}을$\frac{(}{}$를) 얻는 방법으로 제품 공식에서 파생될 수 있습니다.

예:

일부 값

처음 100개의 값(OEIS의 시퀀스 A000010)은 아래 표와 그래프에 나와 있습니다.

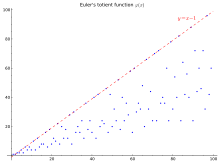
φ(n) for 1 ≤ n ≤ 100

+	1	2	3	4	5	6	7	8	9	10
0	1	1	2	2	4	2	6	4	6	4
10	10	4	12	6	8	8	16	6	18	8
20	12	10	22	8	20	12	18	12	28	8
30	30	16	20	16	24	12	36	18	24	16
40	40	12	42	20	24	22	46	16	42	20
50	32	24	52	18	40	24	36	28	58	16
60	60	30	36	32	48	20	66	32	44	24
70	70	24	72	36	40	36	60	24	78	32
80	54	40	82	24	64	42	56	40	88	24
90	72	44	60	46	72	32	96	42	60	40

오른쪽 상단의 그래프에서 y = n - 1은 하나를 제외한 모든 경우에 유효한 상한이며, n이 소수일 경우에만 구할 수 있습니다. 단순 하한은${\displaystyle }$φ (${\displaystyle \sqrt{n)}}$ ≥ n / 2${\displaystyle \varphi (n)\$geq$${\sqrt {n/2}} 이며, 이는 다소 느슨합니다. 실제로 그래프의 하한은 n/log 로그 n에 비례합니다.

오일러 정리

이것은 만약 a와 n이 상대적으로 소수라면

${\displaystyle a^{\varphi(n)}\equiv 1\mod n.}$

n이 소수인 특별한 경우는 페르마의 작은 정리로 알려져 있습니다.

이것은 라그랑주 정리와 φ(n)이 정수 모듈론의 곱셈군 순서라는 사실로부터 비롯됩니다.

RSA 암호 시스템은 이 정리를 기반으로 합니다. 여기서 e는 (공용) 암호화 지수인 함수 a ↦ a modn의 역수는 함수 b ↦ b modn이고, d는 (사용) 복호화 지수인 e modulo φ(n)의 곱셈 역수입니다. n의 인수분해를 모르는 상태에서 φ(n)을 계산하는 것의 어려움은 따라서 d: n을 인수분해하여 해결할 수 있는 RSA 문제로 알려져 있습니다. RSA 개인 키는 두 개의 큰 소수 p와 q의 곱으로 n을 선택하여 구성되기 때문에 개인 키의 소유자는 인수분해를 알고 있습니다. n만 공개되며, 큰 수의 인수분해가 어렵기 때문에 인수분해를 아는 사람은 아무도 없다는 보장이 있습니다.

기타식

• ${\display style a\mid b\implies \varphi (a)\mid \varphi (b)}$
• ${\displaystyle m\mid \varphi (a^{m}-1)}$
• ${\displaystyle \varphi(mn)=\varphi(m)\varphi(n)\cdot {\frac {d}{\varphi(d))}}\quad {\text{여기서 }d=\operatorname {gcd}(m,n)}$

  특히:

  • ${\displaystyle \varphi(2m)={\begin{case}2\varphi(m)&{\text{}}m{\text{가 짝수}\\\varphi(m)&{\text{가 홀수}\end{case}}$
  • ${\displaystyle \varphi \left(n^{m}\right)=n^{m-1}\varphi(n)}$
• ${\displaystyle \varphi (\operatorname {lcm} (m,n))\cdot \varphi (\operatorname {gcd} (m,n)) =\varphi (m)\cdot \varphi (n)}$

  $\mathrm{공식}$ $\mathrm{lcm}$⁡$($m$,$ $n)$ ⋅ $\gcd$ ⁡($m,$ n) =$$m ⋅ $n {\textstyle \operatorname {lcm}(m,n$)\cdot $\operatorname {$gcd}(m,n)=m\cdot n}(최소공배수 참조)과 비교합니다.

• φ(n) is even for n ≥ 3.

  또한 n이 r개의 뚜렷한 홀수 소인수를 가지면 2 φ(n)

• 4개의 ∤ n이 존재하도록 임의의 a > 1 및 n > 6에 대해 l φ(a - 1)가 되도록 l ≥ 2n이 존재합니다.
• ${\displaystyle {\frac {\varphi(n)}{n}={\frac {\varphi(\operatorname {rad}(n))}{\operator name {rad}(n)}}$

  여기서 rad(n)은 n(n을 나누는 모든 고유한 소수의 곱)의 라디칼입니다.

• ${\displaystyle \sum _{d\mid n}{\frac {\mu ^{2}(d)}{\varphi(d)}={\frac {n}{\varphi(n)}}$ ^[21]
• ${\displaystyle \sum _{1\leq k\leq n \atop(k,n)=1}\!\!k={\tfrac {1}{2}}n\varphi (n)\quad {\text{for }}n>1}$
• ${\displaystyle \sum _{k=1}^{n}\varphi (k)={\tfrac {1}{2}}\left(1+\sum _{k=1}^{n}\mu (k)\left\lfloor {\frac {n}{k}}\right\rfloor ^{2}\right)={\frac {3}{\pi$$^{2}}}n^{2}+O\left(n(\log n)^{\frac {2}{3}}(\log \log n)^{\frac {4}{3}}\right)}$ (^[22] cited in^[23])
• ${\displaystyle \sum _{k=1}^{n}{\frac {\varphi (k)}{k}}=\sum _{k=1}^{n}{\frac {\mu (k)}{k}}\left\lfloor {\frac {n}{k}}\right\rfloor ={\frac {6}{\pi ^{2}}}n+O\left((\log n)^{\frac {2}{3}}(\log \log n)^{\frac {4}{3}}\right)}$ ^[22]
• ${\displaystyle \sum _{k=1}^{n}{\frac {k}{\varphi (k)}}={\frac {315\,\zeta (3)}{2\pi ^{4}}}n-{\frac {\log n}{2}}+O\left((\log n)^{\frac {2}{3}}\right)}$ ^[24]
• ${\displaystyle \sum _{k=1}^{n}{\frac {1}{\varphi(k)}}={\frac {315\,\zeta(3)}{2\pi^{4}}\left(\log n+\gamma -\sum _{p{\text{prime}}}{\frac {\log p}{p^{2}-p+1}}\right)+O\left({\frac {(\log n)^{\frac {2}{3}}}{n}}\right)}$ ^[24]

  (여기서 γ는 오일러-마스케로니 상수입니다.)

• ${\displaystyle \sum _{\stackrel {1\leq k\leq n}{\operatorname {gcd}(k,m)=1}}\!\!\!\!1=n{\frac {\varphi (m)}{m}}+O\left(2^{\omega(m)}\right)}$

  여기서 m > 1은 양의 정수이고 ω(m)은 m의 구별되는 소인수의 수이다.

메논의 정체

1965년 P. 케사바 메논이 증명했습니다.

${\displaystyle \sum _{\stackrel {1\leq k\leq n}{\gcd(k,n)=1}}\!\!\!\!\gcd(k-1,n)=\varphi (n)d(n),}$

여기서 d(n) = σ(n)은 n의 약수의 개수입니다.

임의의 고정된 양의 정수에 의한 나눗셈

« 민속 »의 일부인 다음 속성(즉, 특정 결과로서 명백하게 출판되지 않음: «이 »날 오랫동안 알려진 것으로 명시된 이 기사의 소개 참조)은 중요한 결과를 가져옵니다. 예를 들어 임의의$q$ > 1 ${\displaystyle$q > 1}에 대한 산술 진행$모듈$ q${\displaystyle$ q}에서$$φ(n) ${\displaystyle \varphi$(n)} 값의 균일한 분포를 배제합니다.

• For every fixed positive integer ${\displaystyle q}$, the relation ${\displaystyle q \varphi (n)}$ holds for almost all ${\displaystyle n}$, meaning for all but ${\displaystyle o(x)}$ values of ${\displaystyle n\leq x}$ as ${\displaystyle x\rightarrow \infty }$.

이것은 1개의 모듈로 $q{\displaystyle }$ ${\displaystyle q}$에 일치하는 소수의 역수의 합이 발산한다는$$ 사실의 기본적인 결과이며, 이는 그 자체로 산술 진행에 대한 디리클레 정리의 증명의 결과입니다.

함수를 생성하는 중

φ(n)에 대한 디리클레 급수는 리만 제타 함수로 다음과 같이 표기할 수 있습니다.

${\displaystyle \sum _{n=1}^{\infty }{\frac {\varphi (n)}{n^{s}}}={\frac {\zeta (s-1)}{\zeta (s)}}}$

왼쪽이ℜ($)$ > 2${\displaystyle \Re$s)> 2}(으)로 수렴하는 경우.

Lambert 영상 시리즈 생성 함수는^[27]

${\displaystyle \sum _{n=1}^{\infty }{\frac {\varphi (n)q^{n}}{1-q^{n}}}={\frac {q}{(1-q)^{2}}}}$

q < 1에 수렴합니다.

이 두 가지 모두 기본 시리즈 조작과 φ(n)에 대한 공식으로 증명됩니다.

성장률

Hardy & Wright의 말을 빌리자면, φ(n)의 순서는 "항상 '거의 n'이다."

일단^[29].

${\displaystyle \lim \sup {\frac {\varphi(n)}{n}=1,}$

그러나 n이 무한대로 가면 모든 δ > 0.

${\displaystyle {\frac {\varphi(n)}{n^{1-\delta }}\오른쪽 화살표 \infty .}$

이 두 공식은 φ(n)과 약수 합 함수 σ(n)에 대한 공식 이상을 사용하여 증명할 수 있습니다.

사실 두 번째 공식을 증명하는 동안 부등식은

${\displaystyle {\frac {6}{\pi ^{2}}<{\frac {\varphi(n)\sigma(n)}{n^{2}}<1,}$

n > 1에 대하여 참이며, 증명됩니다.

저희도^[20].

${\displaystyle \lim \inf {\frac {\varphi(n)}{n}}\log \log n=e^{-\gamma }}$

여기서 γ는 오일러 상수인 γ = 0.577215665...이므로 e = 1.7810724... and e^−γ = 0.56145948....

이를 증명하기 위해서는 소수 정리가 필요하지 않습니다.^[31][32] 로그 로그 n은 무한대로 가기 때문에, 이 공식은 다음을 보여줍니다.

${\displaystyle \lim \inf {\frac {\varphi(n)}{n}=0.}$

사실, 더 많은 것이 사실입니다.^[33][34][35]

${\displaystyle \varphi(n)>{\frac {n}{e^{\gamma }\;\log \log n+{\frac {3}{\log \log n}}}}\quad {\text{for}}n>2}$

그리고.

${\displaystyle \varphi(n)<{\frac {n}{e^{\gamma }\log \log n}}\quad {\text{for 무한히 많은}}}$

두 번째 불평등은 장 루이 니콜라스에 의해 나타났습니다. 리벤보임은 "리만 가설이 참이라는 가정 하에서 부등식이 먼저 나타나고, 반대의 가정 하에서 부등식이 나타난다는 점에서 증명 방법은 흥미롭다"고 말합니다.^{[35]: 173}

평균 주문의 경우^[22][36],

${\displaystyle \varphi (1)+\varphi (2)+\cdots +\varphi (n)={\frac {3n^{2}}{\pi^{2}}+O\left(n(\log n)^{\frac {2}{3}}(\log n)^{\frac {4}{3}\right)\quad {\text{as }}n\rightarrow \infty,}$

I. M. 비노그라도프와 N. M. 코로보프에 의한 지수합 추정치를 이용한 증거는 Arnold Walfisz 덕분입니다. 반 데어 코푸트와 비노그라도프의 방법을 조합하여 H.-Q. Liu (Euler's function에 대하여).프록 로이 소크. 에든버러 종파 A 146(2016), No. 4, 769–775)는 오류항을 다음과 같이 개선했습니다.

${\displaystyle O\left(n(\log n)^{\frac {2}{3}}(\log \log n)^{\frac {1}{3}\right)}$

(이것은 현재 이 유형의 추정치 중 가장 잘 알려진 것입니다.) "Big O"는 괄호 안의 n 함수의 상수 배로 경계지어지는 양을 나타냅니다(n에² 비해 작은).

이 결과는 임의로 선택된 두 숫자가 상대적으로 소수일 확률이 6/π임을 증명하는 데 사용될 수 있습니다.

연속된 값의 비율

1950년에 소마야줄루는 증명을^[38][39] 했습니다.

${\displaystyle {\begin{aligned}\lim \inf {\frac {\varphi(n+1)}{\varphi(n)}}&=0\quad {\text{and}}\\[5px]\lim \sup {\frac {\varphi(n+1)}{\varphi(n)}}&=\infty .\end{aligned}}}$

1954년에 쉰젤과 시에르피 ń스키는 이것을 강화하여 세트가

${\displaystyle \left\{\frac {\varphi(n+1)}{\varphi(n)},\;n=1,2,\ldots \right\}$

는 양의 실수로 밀집되어 있습니다. 그들은 또한 세트가^[38]

${\displaystyle \left\{\frac {\varphi(n)}{n}},\;n=1,2,\ldots \right\}$

간격(0,1)에서 조밀합니다.

토텐트 수

토텐트 수는 오일러의 토텐트 함수의 값입니다. 즉, φ(n) = m인 적어도 하나의 n이 존재합니다. 토텐셜 수 m의 원자가 또는 다중성은 이 방정식에 대한 해의 수이다.^[40] 비토텐트는 토텐트 수가 아닌 자연수입니다. 1을 초과하는 모든 홀수 정수는 사소한 비인접수입니다. 또한 짝수 비음수는 무한히 많으며,^[41] 실제로 모든 양의 정수는 짝수 비음수인 배수를 가지고 있습니다.^[42]

주어진 극한 x까지의 토텐트 수는 다음과 같습니다.

${\displaystyle {\frac {x}{\log x}e^{\big (}C+o(1){\big )}(\log \log x)^{2}}$

for a constant C = 0.8178146....^[43]

다중성에 따라 세어 보면, 주어진 극한 x까지의 토텐트 수는

${\displaystyle {\Big \vert }\{n:\varphi (n)\leq x\}{\Big \vert }={\frac {\zeta (2)\zeta (3)}{\zeta (6)}}\cdot x+R(x)}$

여기서 오차항 R은 임의의 양의 k에 대해 최대 x/(로그 x)^k의 순서입니다.^[44]

모든 δ < 0.55655에 대해 m의 다중도가 무한히 자주 m을 초과한다고 알려져 있습니다.

포드 정리

포드(1999)는 모든 정수 k개의 ≥ 2에 대해 총 곱셈 수 m이 존재한다는 것을 증명했습니다. 즉, 방정식 φ(n) = m이 정확하게 k개의 해를 갖는다는 것입니다. 이 결과는 이전에 와크와프 시에르피 ń스키에 의해 추측되었으며, 쉰젤의 가설 H의 결과로 얻어졌습니다. 실제로 발생하는 각 다중성은 무한히 자주 발생합니다.^[43][46]

그러나 다중성 k = 1을 갖는 수 m은 알려져 있지 않습니다. 카마이클의 토션 함수 추측은 그러한 m이 없다는 진술입니다.

퍼펙트 토텐트 수

완벽한 토텐트 수는 반복되는 토텐트의 합과 동일한 정수입니다. 즉, 우리는 숫자 n에 토션트 함수를 적용하고, 그 결과 토션트에 다시 적용하는 등, 숫자 1에 도달할 때까지 그 결과로 나온 수열을 더하면, 합이 n과 같다면, n은 완벽한 토션트 수이다.

적용들

순환절개술

디스퀴지션의 마지막 부분에서 가우스는 φ(n)이 2의 거듭제곱이면 정칙 n각형을 직선과 나침반으로 구성할 수 있음을 증명합니다. 만약 n이 홀수 소수의 거듭제곱이면 토텐셜은 n이 첫 번째 거듭제곱이고 n - 1이 2의 거듭제곱일 경우에만 토텐셜이 2의 거듭제곱이 될 수 있다고 말합니다. 2의 거듭제곱보다 하나 더 많은 소수를 페르마 소수라고 하는데, 3, 5, 17, 257, 65537 등 다섯 가지만 알려져 있습니다. 페르마와 가우스는 이것들을 알고 있었습니다. 그 누구도 더 있는지 증명할 수 없었습니다.

따라서 n이 서로 다른 페르마 소수와 임의의 2의 거듭제곱의 곱이라면, 정규 n곤은 직선과 나침반 구조를 갖습니다. 처음 몇 번은 그런 네어^[52]

2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40,... (OEIS의 시퀀스 A003401).

산술 진행에 대한 소수 정리

RSA 암호 시스템

RSA 시스템을 설정하려면 큰 소수 p 및 q를 선택하고 n = pq 및 k = φ(n)을 계산하고 ed ≡ 1(mod k)과 같은 두 개의 숫자 e 및 d를 찾아야 합니다. 숫자 n과 e("암호화 키")는 공개되고, d("암호화 키")는 비공개로 유지됩니다.

0 < m < n인 정수 m으로 표시되는 메시지는 S = m(modn)을 계산하여 암호화됩니다.

t = S(modn)를 계산하여 복호화합니다. 오일러 정리는 0 < t < n이면 t = m임을 보여주는 데 사용될 수 있습니다.

숫자 n을 효율적으로 인수분해할 수 있거나 n을 인수분해하지 않고 φ(n)을 효율적으로 계산할 수 있다면 RSA 시스템의 보안이 손상될 것입니다.

미해결문제

레메르 추측

p가 prime이면 φ(p) = p - 1입니다. 1932년에 D. H. 레머는 φ(n)가 n - 1을 나누는 합성수 n이 있는지 물었습니다. 알려진 것은 없습니다.

1933년에 그는 그러한 n이 존재한다면 홀수, 사각형이 없어야 하며 적어도 7개의 소수(즉, ω(n) ≥ 7)로 나눌 수 있어야 한다는 것을 증명했습니다. 1980년에 Cohen과 Hagis는 n > 10과 그 ω(n) ≥ 14를 증명했습니다. 또한 Hagis는 3이 n을 나누면 n > 10이고 ω(n) ≥ 298848임을 보여주었습니다.

카마이클 추측

이것은 다른 모든 수 m, m ≠ n, φ(m) ≠ φ(n)에 대해 성질을 갖는 수 n이 없다는 것을 나타냅니다. 위의 포드 정리를 참조하십시오.

본문에서 언급한 바와 같이, 이 추측에 대한 하나의 반례가 존재한다면, 무한히 많은 반례가 존재해야 하며, 가장 작은 반례는 최소 100억 자리 수를 밑 10에 두고 있습니다.^[40]

리만 가설

부등식인 경우에만 리만 가설은 참입니다.

${\displaystyle {\frac {n}{\varphi(n))}<e^{\gamma }\log n+{\frac {e^{\gamma }(4+\gamma -\log 4\pi )}{\sqrt {\log n}}$

는 모든 n개의 ≥ p#에 대하여 참이며, 여기서 γ은 오일러 상수이고 p#은 첫번째 120569개의 소수의 곱입니다.

참고 항목

• 카마이클 기능 (λ)
• 데데킨드 psi 함수(𝜓)
• 약수 함수(σ)

• 더핀-셰퍼 추측
• 페르마의 소정리의 일반화
• 고합성수

• 정수 모듈론의 곱셈군
• 라마누잔합
• 토텐셜 요약 기능(𝛷)

메모들

참고문헌

외부 링크

• "Totient function", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• 오일러의 파이 함수와 중국어 나머지 정리 — Wayback Machine에서 φ(n)가 곱셈적으로 아카이브된다는 증명 2021-02-28
• 자바스크립트에서 오일러 토션 함수 계산기 - 최대 20자리 수
• Dineva, Rosica, The Euler Totient, Möbius, Divisor Functions at Wayback Machine 2021-01-16
• 플라이티지, 루미스, 폴힐 오일러 파이 함수 합산