중앙집중성
Centrality| 시리즈의 일부 | ||||
| 네트워크 과학 | ||||
|---|---|---|---|---|
| 네트워크 타입 | ||||
| 그래프 | ||||
| ||||
| 모델 | ||||
| ||||
| ||||
그래프 이론 및 네트워크 분석에서 중심성 지표는 네트워크 위치에 대응하는 그래프 내의 노드에 숫자 또는 순위를 할당합니다.응용 프로그램에는 소셜 네트워크에서 가장 영향력 있는 사람, 인터넷 또는 도시 네트워크의 주요 인프라 노드, 질병 확산자 및 뇌 네트워크의 [1][2]식별이 포함됩니다.중심성 개념은 소셜 네트워크 분석에서 처음 개발되었으며, 중심성을 측정하기 위해 사용되는 많은 용어들은 그들의 사회학적 [3]기원을 반영한다.
중심성 지수의 정의 및 특성화
중심성 지수는 "중요한 정점을 특징짓는 것은 무엇인가?"라는 질문에 대한 대답입니다.답은 그래프의 꼭지점에 대한 실수치 함수의 관점에서 제시되며, 여기서 생성된 값은 가장 중요한 [4][5][6]노드를 식별하는 순위를 제공할 것으로 예상된다.
"중요성"이라는 단어는 많은 의미를 가지며, 중심성에 대한 많은 다른 정의로 이어집니다.두 가지 분류 방식이 제안되었다.「중요성」은, 네트워크상의 플로우나 전송의 타입에 관련지어 생각할 수 있습니다.이것에 의해,[5] 중심부를 중요하다고 간주하는 플로우의 타입에 의해서 분류할 수 있습니다.「중요성」은, 네트워크의 응집력에 관여하는 것으로 생각할 수도 있습니다.이를 통해 중앙집권부를 [7]응집력을 측정하는 방법에 따라 분류할 수 있습니다.이 두 가지 접근법 모두 중앙집권성을 다른 범주로 나눕니다.또 하나의 결론은 한 카테고리에 적합한 중심성은 다른 [5]카테고리에 적용되면 종종 "잘못"된다는 것입니다.
전부는 아니지만 많은 중심성 측정이 특정 정점을 통과하는 유형의 경로 수(보행이라고도 함)를 효과적으로 계산한다. 측정치는 관련 보행을 정의하고 계산하는 방법에 따라 다르다.이 그룹에 대한 고려를 제한하면 길이 1단계(도 중심성)에서 무한 단계(유전자 중심성)[4][8]까지 스펙트럼에 많은 중심성을 배치하는 분류법이 가능하다.between centrality와 같은 다른 중앙 집중성 척도는 전체적인 연결성뿐만 아니라 네트워크 연결에 중추적인 위치를 차지하는 데 초점을 맞춥니다.
네트워크 흐름에 의한 특성화
네트워크는 어떤 것이 흐르는 경로에 대한 설명으로 간주할 수 있습니다.이것에 의해, 플로우의 타입과 센트럴리티에 의해서 부호화된 패스의 타입에 근거해 특성을 지정할 수 있습니다.플로우는 전송에 근거할 수 있습니다.이 전송에서는, 각 분할할 수 없는 항목이 1개의 노드에서 다른 노드로 이동합니다.예를 들면, 배송 사이트에서 클라이언트의 자택으로 이동하는 패키지 배송과 같습니다.두 번째 경우는 직렬 복제입니다. 이 경우 항목이 복제되어 원본과 대상이 모두 해당 항목이 복제됩니다.예를 들어 가십을 통한 정보 전파는 개인 방식으로 정보가 전파되며 프로세스 종료 시 소스 노드와 타깃 노드 모두에 정보가 통지됩니다.마지막 경우는 병렬 복제입니다.이 경우 항목이 동시에 여러 링크로 복제됩니다.예를 들어 라디오 브로드캐스트는 [5]동시에 많은 청취자에게 동일한 정보를 제공합니다.
마찬가지로 경로의 유형은 측지학(최단 경로), 경로(정점을 두 번 이상 방문하지 않음), 추적(정점을 여러 번 방문할 수 있음, 모서리를 두 번 이상 횡단할 수 없음) 또는 산책(정점과 모서리를 여러 [5]번 방문/이동할 수 있음)으로 제한할 수 있습니다.
보행구조별 특성화
다른 분류는 중심성을 구성하는 방법에서 도출할 수 있다.이것은 다시 두 개의 클래스로 분할됩니다.중심은 방사형 또는 중앙입니다.반경 중심 카운트는 지정된 정점에서 시작/종료되는 보행입니다.정도 및 고유값 중심은 길이 1 또는 길이 무한대의 보행 수를 세는 반지름 중심부의 예입니다.중앙 중심은 지정된 정점을 통과하는 걷기를 카운트합니다.전형적인 예는 주어진 [7]정점을 통과하는 최단 경로의 수인 프리먼의 중간성 중심성이다.
마찬가지로, 카운트는 보행량 또는 길이 중 하나를 캡처할 수 있습니다.볼륨은 지정된 유형의 총 보행 수입니다.이전 단락의 세 가지 예가 이 범주에 속합니다.길이는 그래프의 지정된 정점에서 나머지 정점까지의 거리를 캡처합니다.주어진 정점에서 다른 모든 정점까지의 총 측지선 거리인 근접성 중심은 가장 잘 알려진 [7]예입니다.이 분류는 보행 카운트 유형(예: 보행, 산책로, 경로, 측지학)과 무관하다.
Borgatti와 Everett은 이 유형학이 중심성 측정치를 가장 잘 비교할 수 있는 방법에 대한 통찰력을 제공한다고 제안한다.이 2×2 분류에서 같은 상자에 배치된 중심은 타당한 대안을 만들기에 충분히 유사하다. 어떤 것이 주어진 애플리케이션에 더 나은지를 합리적으로 비교할 수 있다.그러나 상자마다 측정값이 다릅니다.상대 적합성에 대한 평가는 어느 범주가 더 적합한지 미리 결정하는 컨텍스트 내에서만 수행될 수 있으므로 비교 [7]결과를 도출할 수 있습니다.
반경 부피 중심은 스펙트럼에 존재한다.
보행 구조에 의한 특성화는 널리 사용되는 거의 모든 중심부가 반경 체적 측정임을 보여준다.이것들은 정점의 중심성이 정점과 연관된 정점의 중심성의 함수라는 믿음을 부호화한다.중앙집권에서는 연관성이 어떻게 정의되는지를 구별합니다.
보나치치는 연관성이 보행의 관점에서 정의되는 경우 [4]고려된 보행 길이에 기초하여 중심 집단을 정의할 수 있음을 보여주었다.정도 중심성은 길이의 보폭을 1로 카운트하고 고유값 중심성은 길이의 보폭을 무한대로 카운트합니다.연관성에 대한 대체 정의도 합리적입니다.알파 중심성은 정점이 외부 영향원을 가질 수 있도록 합니다.에스트라다의 서브그래프 중심성은 닫힌 경로(삼각형, 정사각형 등)만 세는 것을 제안한다.
이러한 측정의 핵심은 그래프의 인접 행렬의 검정력이 해당 검정력에 의해 주어진 길이의 도보 수를 제공한다는 관찰이다.마찬가지로, 행렬 지수 역시 주어진 길이의 보행 수와 밀접하게 관련되어 있습니다.인접 매트릭스의 초기 변환에 의해 워크카운트 타입을 다른 정의할 수 있습니다.어느 접근법에서도 정점의 중심성은 무한합으로 표현될 수 있다.
행렬 검정력 또는
행렬 지수, 여기서
- k는 보행길이입니다.
- 은 변환된 인접관계 매트릭스입니다.
- β는 합계의 수렴을 보장하는 할인 파라미터입니다.
Bonacich의 일련의 척도는 인접 행렬을 변환하지 않습니다.알파 집중성은 인접 매트릭스를 해결 매트릭스로 바꿉니다.서브그래프의 중앙집중성은 인접 매트릭스를 트레이스로 대체합니다.놀라운 결론은 인접 행렬의 초기 변환에 관계없이 이러한 접근법에는 모두 공통 제한 동작이 있다는 것입니다.β가 0에 가까워짐에 지수는 차수의 중심으로 수렴됩니다.β가 최대값에 가까워지면 는 고유값 [8]중심성으로 수렴된다.
게임 이론의 중심성
전술한 표준척도의 대부분은 노드가 스스로 수행하는 역할에만 초점을 맞추어 노드의 중요성을 평가한다는 것이 공통적인 특징입니다.그러나 많은 애플리케이션에서 그러한 접근법은 노드 기능을 그룹으로 고려할 경우 발생할 수 있는 시너지 때문에 부적절하다.
예를 들어, 전염병을 막는 문제에 대해 생각해 보겠습니다.위의 네트워크 이미지를 보고 어떤 노드에 예방접종을 해야 하나요?앞에서 설명한 조치를 바탕으로 질병 확산에 가장 중요한 노드를 인식하고 싶다.노드의 개별 기능에 초점을 맞춘 중앙 집중식 접근 방식은 좋지 않을 수 있습니다.붉은 사각형에 있는 노드들은 개별적으로 질병 확산을 멈출 수 없지만, 이들을 그룹으로 볼 때 v5에서 시작된 경우 질병을 멈출 수 있음을 명확히 알 수 있습니다.게임 이론의 중심성은 문제를 설명하려고 합니다.게임 플레이어의 도구를 사용하여 렘과 기회를 제공합니다.에서 제안하는 접근방식은 섀플리 값을 사용합니다.섀플리 값 계산의 시간 복잡도 경도 때문에 이 영역의 대부분의 노력은 네트워크의 고유한 토폴로지 또는 문제의 특수 특성에 의존하는 새로운 알고리즘과 방법을 구현하기 위해 이루어집니다.이러한 접근방식은 시간 복잡성을 지수에서 다항식으로 감소시킬 수 있다.
마찬가지로 솔루션 개념 권한 분포()[10]는 참가자 간의 직접적인 영향을 측정하기 위해 섀플리 값이 아닌 섀플리-슈빅 검정력 지수를 적용한다.분포는 실제로 고유 벡터 중심성의 한 유형입니다.Hu(2020년)[11]의 빅데이터 객체를 정렬하는 데 사용되며, 예를 들어 미국 대학의 순위를 매기는 데 사용됩니다.
중요한 제한 사항
중심성 지수에는 두 가지 중요한 한계가 있는데 하나는 명백한 한계이고 다른 하나는 미묘한 한계이다.분명한 한계는 한 애플리케이션에 최적인 중앙 집중성이 다른 애플리케이션에 최적이 아닌 경우가 많다는 것입니다.사실 그렇지 않았다면 이렇게 많은 중앙집권제가 필요하지 않았을 것이다.이 현상의 예시는 크랙하르트 연 그래프에 의해 제공되며, 중심성의 세 가지 다른 개념은 가장 중심적인 [12]정점의 세 가지 다른 선택을 제공한다.
더 미묘한 한계는 정점 중심성이 정점의 상대적 중요성을 나타낸다는 일반적인 오류입니다.중심성 지수는 가장 중요한 [4][5]정점을 나타낼 수 있는 순위를 생성하도록 명시적으로 설계된다.방금 언급한 제한하에서 그들은 잘 해낸다.일반적으로 노드의 영향을 측정하도록 설계되지 않았습니다.최근 네트워크 물리학자들은 이 문제에 대처하기 위해 노드 영향 메트릭을 개발하기 시작했습니다.
오류는 이중입니다.첫째, 순위는 중요도에 따라 정점을 정렬할 뿐, 순위의 여러 수준 간의 중요도 차이를 정량화하지 않는다.이는 Freeman의 중앙집중화를 문제의 중앙집중성 측정에 적용함으로써 완화될 수 있습니다.이 척도는 중앙집중성 점수의 차이에 따라 노드의 중요성을 어느 정도 파악할 수 있습니다.게다가 Freeman의 일원화를 사용하면, 복수의 네트워크의 최고 집중 [13]스코어를 비교하는 것으로써, 복수의 네트워크를 비교할 수 있습니다.그러나 이 접근방식은 [citation needed]실제에서는 거의 볼 수 없습니다.
둘째, 특정 네트워크/애플리케이션에서 가장 중요한 정점을 (올바르게) 식별하는 기능이 반드시 나머지 정점으로 일반화되는 것은 아닙니다.대부분의 다른 네트워크 노드에서 순위는 [14][15][16][17]무의미할 수 있습니다.예를 들어 Google 이미지 검색의 처음 몇 개의 결과만 적절한 순서로 표시되는 이유를 설명합니다.호출기는 점프 [18]매개변수를 약간 조정한 후 빈번한 순위 역전을 보이는 매우 불안정한 측정치이다.
중앙집중성지수가 네트워크의 나머지 부분에 대해 일반화하지 못하는 것은 처음에는 반직관적으로 보일 수 있지만, 이는 위의 정의에서 직접 나옵니다.복잡한 네트워크에는 이종 토폴로지가 있습니다.최적의 측정이 가장 중요한 정점의 네트워크 구조에 따라 달라지는 한,[14] 그러한 정점에 최적인 측정은 네트워크의 나머지 부분에 대해 차선책이다.
정도 중심성
역사적으로 첫 번째이자 개념적으로 가장 단순한 것은 정도 중앙집중성입니다.이 중앙집중성은 노드에 입사하는 링크의 수(즉, 노드가 가지고 있는 넥타이 수)로 정의됩니다.정도는 네트워크를 통과하는 모든 것(바이러스나 일부 정보 등)을 포착하기 위한 노드의 즉각적인 위험으로 해석할 수 있습니다.다이렉트 네트워크의 경우(유리에 방향이 있는 경우), 보통 indegree와 outdegree의 두 가지 정도 중심성 척도를 정의합니다.따라서 indegree는 노드로 향하는 연결 개수이고 outdegree는 노드가 다른 노드로 향하는 연결 개수입니다.유대관계가 우정이나 협업과 같은 긍정적인 측면과 연관될 때, 인디그리는 종종 인기의 한 형태로 해석되고 사교성으로 해석됩니다.
{의 정점과E { E 개의 모서리가 그래프 G : ( , ) { G : ( V , )}에 대한 v { v의 중심도는 다음과 같이 정의됩니다.
그래프의 모든 노드에 대한 정도 중심성 계산에는 그래프의 밀도 인접 행렬 표현에서 (2)가 소요되며, 에지에 대해서는 희박한 행렬 표현에서 (가 소요됩니다.
노드 레벨에서의 중앙 집중성의 정의는 그래프 전체로 확장될 수 있습니다.이 경우 그래프 [19]집중화에 대해 설명합니다. { v* } 를 G{ G} 에서 중심도가 가장 높은 노드로 합니다 ( Y ,) { X : = ( Y , ) 노드 연결 그래프는 중심도가 높은 Y { Y 입니다. X
이에 대응하여 G(\ G의 집중도는 다음과 같습니다.
에 다른 모든 노드가 연결되어 있는 중앙 노드가 하나(별 그래프) 포함되어 있는 경우H(\ H 이 최대화됩니다.
따라서 G : ( ,), {\ G : = E ) }
또한 Trendance to Make Hub(TMH)라는 이름의 학위 중심성에 대한 새로운 광범위한 글로벌 척도는 다음과 [2]같이 정의됩니다.
여기서 TMH는 네트워크의 중심 정도에 따라 증가합니다.
근접성 중심
접속 그래프에서 노드의 정규화된 근접도 중심(또는 근접도)은 그래프 내의 노드와 다른 모든 노드 사이의 최단 경로의 평균 길이입니다.따라서 노드가 중앙일수록 다른 모든 노드에 더 가깝습니다.
근접도는 Alex Bavelas(1950)에 의해 원근도의 [20][21]역수로서 정의되었습니다., C B( ) ( ,v) - ( \ C _ { } ( v ) ( \ _ {} d( , v )^ -( \ sum _ { u distance , )v )그러나 근접성 중심성에 대해 언급할 때, 사람들은 일반적으로 N -을 곱한 이전 공식에서 정규화된 형식을 참조합니다. 서 N N은 그래프에서 노드 수입니다.
이 정규화를 통해 크기가 다른 그래프의 노드 간 비교를 할 수 있다.많은 그래프에서 근접도 역수와 [22]정도 로그(v) - µ - lnδ ( v) +β ( \ ( ) ) \ - ( k _ { v ) + \ } ( k v )는 강한 상관관계가 있다. 서 k {{ _ { 는 }의 정점과 β}도이다.
다른 모든 노드와의 거리는 무방향 그래프와는 무관하지만 방향 그래프에서는 전혀 다른 결과를 얻을 수 있습니다(예: 웹사이트는 발신 링크에서 높은 근접성 중심성을 가질 수 있지만 착신 링크에서 낮은 근접성 중심성을 가질 수 있습니다).
조화 중심성
(꼭 연결되어 있을 필요는 없는) 그래프에서 고조파 중심성은 근접도 중심성의 정의에서 합계와 상호 연산을 반전시킵니다.
서u에서 v로의 경로가없는 1/(u ,v ) 0 {{1/)=입니다. 고조파 중심성은N -({로 나누어 정규화할 수 있습니다. 서N { N은 그래프 내의 노드 수입니다.
조화 중심성은 Marchiori와 Latora(2000년)[23]에 의해 제안되었고, 그 후 Dekker(2005년)에 의해 독립적으로 "가치 중심성"[24]이라는 이름을 사용하며 Rochat(2009년)[25]에 의해 제안되었다.
중심성
betweeness는 그래프 내 정점의 중심성 측도입니다(여기에서는 설명하지 않습니다).betweenness centrality는 노드가 다른 두 노드 간의 최단 경로를 따라 브리지로 동작하는 횟수를 수량화합니다.그것은 린튼 [26]프리먼이 소셜 네트워크에서 다른 인간들 간의 의사소통에 대한 인간의 통제를 수량화하기 위한 척도로 도입했다.그의 개념에서, 무작위로 선택된 두 꼭지점 사이의 무작위로 선택된 최단 경로에서 발생할 확률이 높은 꼭지점은 높은 중간성을 가진다.
G :( , E) { G : ( , ) { displaystyle V}의 v { v}의 간격은 다음과 같이 계산됩니다.
- 각 꼭지점 쌍(s,t)에 대해 꼭지점 사이의 최단 경로를 계산합니다.
- 각 정점 쌍(s,t)에 대해 해당 정점(여기서 정점 v)을 통과하는 최단 경로의 비율을 결정합니다.
- 이 분수를 모든 정점 쌍(s,t)에 걸쳐 합합니다.
좀 더 간결하게 표현하면 다음과 같습니다.[27]
서 s \ \ _ { }는 에서 t \ t로 가는 최단 경로의 총수이며, (){ \ v}를 하는 경로의 개수입니다.v를 포함하지 않는 정점 쌍의 수를 분할하여 정규화할 수 있습니다.유향 그래프의 경우 ( ) (-2 무방향 그래프의(-1 ) ( -2) / \display ( n - 1 ) ( n -)입니다예를 들어, 무방향 그래프의 경우, 무방향 중앙의 경우,(- 1 )( -) / ( n - 2 ) ( n - 2 ) / 2 ( n - () ( ) /) (정규화된 경우)의 간격은 0이 됩니다.
계산 측면에서 그래프 내 모든 정점의 간극과 근접도 중심에는 그래프 상의 모든 정점 쌍 사이의 최단 경로가 계산됩니다. 이를 위해서는 Floyd-Warshall 알고리즘을 사용하여 O3 O시간이 합니다.단, 희박한 그래프에서는 Johnson 알고리즘이 O logV + )(\}\ 시간이 때문에 보다 효율적일 수 있습니다.가중치가 없는 그래프의 경우 O E O시간이 Brandes 알고리즘을[27] 사용하여 계산할 수 있습니다.일반적으로 이러한 알고리즘은 그래프가 무방향이며 루프 및 다중 에지를 허용하여 연결되어 있다고 가정합니다.네트워크 그래프를 구체적으로 다룰 때 그래프에는 단순한 관계를 유지하기 위해 루프나 여러 모서리가 없는 경우가 많습니다(여기서 모서리는 두 사람 또는 정점 사이의 연결을 나타냅니다).이 경우 Brandes 알고리즘을 사용하면 2회 [27]카운트되는 각 최단 경로를 설명하기 위해 최종 집중도 점수를 2로 나눈다.
고유 벡터 중심성
고유 벡터 중심성(고유 중심성이라고도 함)은 네트워크 내 노드의 영향을 측정하는 척도입니다.고득점 노드로의 접속이 저득점 [28][6]노드로의 동등한 접속보다 해당 노드의 점수에 더 많은 영향을 미친다는 개념에 따라 네트워크 내의 모든 노드에 상대적인 점수를 할당합니다.구글의 PageRank와 Katz의 중심성은 고유 벡터 [29]중심성의 변형이다.
인접 행렬을 사용하여 고유 벡터 중심성 찾기
주어진 G : ( ,) { G : = ( , ) { V 의 경우 A ( ,t) { A = ( { , ) } 를 인접 행렬, 즉 , { a }, } 로 . , t (\0).의 상대 점수는 다음과 같이 정의할 수 있습니다.
서 M v은 v{ v의 네이버 세트이고 "{는 상수입니다.작은 재배열로 이것은 벡터 표기법으로 고유 벡터 방정식으로 다시 쓰여질 수 있다.
일반적으로 0이 아닌 고유 벡터 솔루션이 존재하는 고유값(\는 여러 가지가 있습니다.인접행렬의 엔트리는 음이 아니기 때문에 Perron-Frobenius 정리에 의해 유일하게 가장 큰 고유값이 존재합니다.이 가장 큰 고유값은 원하는 중심성 [30]측정값입니다.그런 다음 관련 고유 의 v h {\}} 컴포넌트는 에서 v v의 상대적인 중심성 점수를 제공합니다.고유 벡터는 공통 요인까지만 정의되므로 정점의 중심 비율만 잘 정의됩니다.절대 점수를 정의하려면 고유 벡터를 정규화해야 합니다. 예를 들어 모든 정점에 걸친 합계가 1 또는 정점 n의 총 수가 되도록 해야 합니다.검정력 반복은 이 주요 고유 [29]벡터를 찾는 데 사용할 수 있는 여러 고유값 알고리즘 중 하나입니다.또, A의 엔트리가 확률행렬과 같이 접속 강도를 나타내는 실수일 수 있도록 일반화 할 수 있다.
카츠 중심
Katz 중심성은[31] 정도 중심성의 일반화이다.Degree centrality는 직접 네이버의 수를 측정하고 Katz centrality는 경로를 통해 연결할 수 있는 모든 노드의 수를 측정합니다.단, 원거리 노드의 기여는 불이익을 받습니다.수학적으로는 다음과 같이 정의됩니다.
서α {\\는 (감쇠 계수입니다
Katz 중심성은 고유 벡터 중심성의 변형으로 볼 수 있습니다.Katz 중심성의 또 다른 형태는
고유 벡터의 중심성 표현과 비교하여 j(\는 x +로 대체됩니다
주 고유 벡터( 고유값과 관련됨, 인접 행렬)는 α \alpha가 아래에서 1µ{1}{\}})에 에 Katz 중심성의 한계인 것으로 나타났다[32].
PageRank의 일원성
PageRank는 다음 방정식을 충족합니다.
어디에
는 의 네이버 수(또는 방향 아웃바운드링크 수)입니다.고유 벡터 중심성 및 Katz 중심성과 비교하여 한 가지 큰 차이는 스케일링 () \ L ( j) 。 PageRank 와 고유 벡터 중심성의 또 다른 차이점은 pageRank 벡터가 좌측 고유 벡터라는 것입니다( 가 [33]반전되었다는 점에 유의하십시오).
침투 집중성
복잡한 네트워크에서 단일 노드의 '중요성'을 결정하기 위해 많은 중앙 집중성 측정이 존재합니다.단, 이러한 척도는 순수하게 토폴로지적인 관점에서 노드의 중요성을 정량화하고 노드의 값은 노드의 '상태'에 좌우되지 않는다.네트워크 다이내믹스에 관계없이 일정하게 유지됩니다.이는 가중치 간 측정에도 해당된다.단, 노드는 중간집중성 또는 다른 중심집중성 측정의 관점에서 매우 잘 중앙에 위치할 수 있지만 침투가 있는 네트워크의 맥락에서 '중앙'에 위치할 수 없습니다.「컨태지온」의 침투는, 복수의 시나리오에서 복잡한 네트워크내에서 발생합니다.예를 들어, 바이러스나 박테리아 감염은 접촉 네트워크라고 알려진 사람들의 소셜 네트워크를 통해 확산될 수 있다.질병 확산은 또한 도로, 철도 또는 항공 연결로 연결된 도시 또는 인구 중심 네트워크를 고려함으로써 더 높은 추상화 수준에서 고려될 수 있다.컴퓨터 바이러스는 컴퓨터 네트워크에 퍼질 수 있다.사업 제안과 거래에 대한 소문이나 뉴스는 사람들의 소셜 네트워크를 통해서도 퍼질 수 있다.이러한 모든 시나리오에서 복잡한 네트워크의 링크에 걸쳐 '경합'이 확산되어 노드의 '상태'가 복구 가능 또는 기타 방법으로 변경됩니다.예를 들어, 역학 시나리오에서 개인은 감염이 확산됨에 따라 '감시할 수 있는' 상태에서 '감시할 수 있는' 상태로 변한다.위의 예에서 개별 노드가 취할 수 있는 상태는 바이너리(예를 들어 뉴스를 수신/수신하지 않음), 이산(감시 가능/감염/복구됨), 또는 전염 확산에 따라 연속(예를 들어 마을 내 감염자 비율)일 수 있습니다.이러한 모든 시나리오에서 공통적인 특징은 전염의 확산으로 인해 네트워크의 노드 상태가 변화한다는 것입니다.이를 염두에 두고 Percolation Centrality(PC; 침투 집중성)가 제안되었습니다.이것은 네트워크를 통한 침투 지원 측면에서 노드의 중요성을 구체적으로 측정합니다.이 조치는 피라베난 등에 의해 제안되었다.[34]
침투 집중성은 특정 노드에 대해 특정 시간에 해당 노드를 통과하는 '투과 경로'의 비율로 정의됩니다.'투과 경로'는 소스 노드가 투과(예: 감염)되는 노드 쌍 사이의 최단 경로입니다.타깃 노드는 투과 또는 비투과 또는 부분적으로 투과된 상태로 할 수 있습니다.
서 s r{\은 s {\ s에서 r {\r에 대한 최단 경로의 총수이며, 는v {\v를 하는 경로의 수입니다. i의t {\t의 침투 상태는 로 , {\}=인 로, x t{\ t의 비침투 상태를 나타낸다. i { {^ { { i }1 。 t{ t 중간 값은 부분적으로 침투된 상태를 나타냅니다(예를 들어, 읍면 네트워크에서 이는 해당 마을에서 감염된 사람의 비율입니다).
송신원노드의 투과레벨이 높을수록 그 노드에서 발신되는 경로가 중요하다는 전제 하에 투과패스에 부가된 가중치는 송신원노드에 할당된 투과레벨에 따라 달라집니다.따라서 고도로 침투된 노드에서 발생하는 최단 경로에 있는 노드는 침투에 더 중요할 수 있습니다.PC의 정의는 타겟노드의 가중치를 포함하도록 확장될 수도 있습니다.침투 중심성 계산은 Brandes의 고속 알고리즘에서 채택한 효율적인 구현으로 O M 시간(\ O(으로 실행되며, 계산에서 목표 노드의 가중치를 고려할 필요가 있는 경우 가장 나쁜 시간은3)\3입니다.
크로스 클리크 일원화
복잡한 그래프에서 단일 노드의 교차 클리크 집중도에 따라 다른 CLI에 대한 노드 연결이 결정됩니다.크로스 클리크 접속성이 높은 노드를 사용하면 그래프 내의 정보나 질병의 전파가 용이해집니다.클리크는 각 노드가 클리크 내의 다른 모든 노드에 연결되어 있는 서브그래프입니다. G : ( ,) \ G := ( , )} 와 E \ E 엣지의 { v}의 크로스 클리크 연결은 ( ) ( X。v {\ v이(가) 속하는 큐입니다.이 방안은 에서 사용되었지만 1998년 에버렛과 보가티가 처음 제안했으며, 그들은 그것을 파벌-오버랩 중심이라고 불렀다.
프리먼의 일원화
네트워크의 집중화는 다른 모든 노드의 [13]집중도와 비교하여 네트워크의 가장 집중적인 노드가 얼마나 집중적인지를 나타내는 척도입니다.다음으로 집중화 대책은 (a) 네트워크 내의 가장 중심적인 노드와 다른 모든 노드 간의 중심성 차이의 합계를 계산하고 (b) 이 양을 같은 [13]규모의 네트워크 내의 이론상 가장 큰 차이의 합으로 나눈다.따라서 모든 중앙 집중성 척도는 고유한 중앙 집중화 척도를 가질 수 있습니다. x( i) { C _ { } ( _ { } )가 의 중심성 측정치인 , C ( ) { C _ { } ( p _ { *} )가 네트워크에서 가장 큰 측정치인 , 다음과 같은 경우 공식적으로 정의됩니다.
는 노드 수가 같은 그래프에 대한 포인트 x {\의 최대 차이 합계입니다.네트워크의 집중화는 다음과 같습니다.[13]
그 컨셉은 린튼 프리먼 때문이다.
차이점 기반 중앙 집중성 측정
특정 네트워크의 노드 랭킹에서 더 나은 결과를 얻기 위해 (분류 이론과 데이터 마이닝 이론에 특유한) 차이성 척도를 사용하여 복잡한 네트워크에서의 집중성 척도를 강화한다.이것은 고유값 문제의 해답을 통해 각 노드의 중심성을 계산하는 고유 벡터 중심성으로 설명된다.
서 }=좌표 대 조정 제품) {ij는 임의의 차이 매트릭스로, 예를 들어 Jaccard의 차이점에 의해 정의된다.
이 측정에서 각 노드의 토폴로지적 기여(기여 중심성이라고 하는 이유)를 정량화할 수 있으며, 가중치/관련성이 큰 노드는 자신이 직접 액세스할 수 없는 노드에 액세스할 수 있기 때문이다.
때문에 한{A\displaystyle}그리고 D{D\displaystyle} 있non-negative 매트릭스 그래서 우리는 위의 문제 cnon-negative과λ)λmax의 netw에 각 노드의 중심을 추론할 수 있도록 한데 따른 독특한 해결책을 가지고 있도록 Perron–Frobenius 원칙을 사용할 수 있는 W{W\displaystyle},non-negative은 주목됩니다.오케스트라.따라서 i번째 노드의 중심은
서 nn은 네트워크 내의 노드 수입니다.연구 사례에서 개선된 결과를 얻기 위해 몇 가지 차이점 측정과 네트워크가 테스트되었다.
「 」를 참조해 주세요.
주 및 참고 자료
- ^ van den Heuvel MP, Sporns O (December 2013). "Network hubs in the human brain". Trends in Cognitive Sciences. 17 (12): 683–96. doi:10.1016/j.tics.2013.09.012. PMID 24231140. S2CID 18644584.
- ^ a b Saberi M, Khosrowabadi R, Khatibi A, Misic B, Jafari G (January 2021). "Topological impact of negative links on the stability of resting-state brain network". Scientific Reports. 11 (1): 2176. doi:10.1038/s41598-021-81767-7. PMC 7838299. PMID 33500525.
- ^ 뉴먼, M.E.J. 2010년네트워크: 개요옥스포드, 영국: 옥스포드 대학 출판부.
- ^ a b c d Bonacich, Phillip (1987). "Power and Centrality: A Family of Measures". American Journal of Sociology. 92 (5): 1170–1182. doi:10.1086/228631. S2CID 145392072.
- ^ a b c d e f Borgatti, Stephen P. (2005). "Centrality and Network Flow". Social Networks. 27: 55–71. CiteSeerX 10.1.1.387.419. doi:10.1016/j.socnet.2004.11.008.
- ^ a b Christian F. A. Negre, Uriel N. Morzan, Heidi P. Hendrickson, Rhitankar Pal, George P. Lisi, J. Patrick Loria, Ivan Rivalta, Junming Ho, Victor S. Batista. (2018). "Eigenvector centrality for characterization of protein allosteric pathways". Proceedings of the National Academy of Sciences. 115 (52): E12201–E12208. doi:10.1073/pnas.1810452115. PMC 6310864. PMID 30530700.
{{cite journal}}: CS1 maint: 여러 이름: 작성자 목록(링크) - ^ a b c d Borgatti, Stephen P.; Everett, Martin G. (2006). "A Graph-Theoretic Perspective on Centrality". Social Networks. 28 (4): 466–484. doi:10.1016/j.socnet.2005.11.005.
- ^ a b Benzi, Michele; Klymko, Christine (2013). "A matrix analysis of different centrality measures". SIAM Journal on Matrix Analysis and Applications. 36 (2): 686–706. arXiv:1312.6722. doi:10.1137/130950550. S2CID 7088515.
- ^ 미할락, 아디티야, 슈체판스키, 라빈드란, 제닝스 arXiv: 1402.0567
- ^ Hu, Xingwei; Shapley, Lloyd (2003). "On Authority Distributions in Organizations". Games and Economic Behavior. 45: 132–170. doi:10.1016/s0899-8256(03)00130-1.
- ^ Hu, Xingwei (2020). "Sorting big data by revealed preference with application to college ranking". Journal of Big Data. 7. arXiv:2003.12198. doi:10.1186/s40537-020-00300-1.
- ^ Krackhardt, David (June 1990). "Assessing the Political Landscape: Structure, Cognition, and Power in Organizations". Administrative Science Quarterly. 35 (2): 342–369. doi:10.2307/2393394. JSTOR 2393394.
- ^ a b c d Freeman, Linton C. (1979), "centrality in social networks: Conceptual clarification" (PDF), Social Networks, 1 (3): 215–239, CiteSeerX 10.1.1.227.9549, doi:10.1016/0378-8733(78)90021-7, archived from the original (PDF) on 2016-02-22, retrieved 2014-07-31
- ^ a b Lawyer, Glenn (2015). "Understanding the spreading power of all nodes in a network: a continuous-time perspective". Sci Rep. 5: 8665. arXiv:1405.6707. Bibcode:2015NatSR...5E8665L. doi:10.1038/srep08665. PMC 4345333. PMID 25727453.
- ^ da Silva, Renato; Viana, Matheus; da F. Costa, Luciano (2012). "Predicting epidemic outbreak from individual features of the spreaders". J. Stat. Mech.: Theory Exp. 2012 (7): P07005. arXiv:1202.0024. Bibcode:2012JSMTE..07..005A. doi:10.1088/1742-5468/2012/07/p07005. S2CID 2530998.
- ^ Bauer, Frank; Lizier, Joseph (2012). "Identifying influential spreaders and efficiently estimating infection numbers in epidemic models: A walk counting approach". Europhys Lett. 99 (6): 68007. arXiv:1203.0502. Bibcode:2012EL.....9968007B. doi:10.1209/0295-5075/99/68007. S2CID 9728486.
- ^ Sikic, Mile; Lancic, Alen; Antulov-Fantulin, Nino; Stefanic, Hrvoje (2013). "Epidemic centrality -- is there an underestimated epidemic impact of network peripheral nodes?". The European Physical Journal B. 86 (10): 1–13. arXiv:1110.2558. Bibcode:2013EPJB...86..440S. doi:10.1140/epjb/e2013-31025-5. S2CID 12052238.
- ^ Ghoshal, G.; Barabsi, A L (2011). "Ranking stability and super-stable nodes in complex networks". Nat Commun. 2: 394. Bibcode:2011NatCo...2..394G. doi:10.1038/ncomms1396. PMID 21772265.
- ^ Freeman, Linton C. "소셜 네트워크의 중심 개념 명확화"소셜 네트워크 1.3(1979) : 215 ~239.
- ^ 알렉스 바벨라스.태스크 지향 그룹의 통신 패턴.J. 어쿠스틱 Soc.Am, 22(6):725-730, 1950.
- ^ Sabidussi, G (1966). "The centrality index of a graph". Psychometrika. 31 (4): 581–603. doi:10.1007/bf02289527. hdl:10338.dmlcz/101401. PMID 5232444. S2CID 119981743.
- ^ Evans, Tim S.; Chen, Bingsheng (2022). "Linking the network centrality measures closeness and degree". Communications Physics. 5 (1): 172. doi:10.1038/s42005-022-00949-5. ISSN 2399-3650. S2CID 236881169.
- ^ Marchiori, Massimo; Latora, Vito (2000), "Harmony in the small-world", Physica A: Statistical Mechanics and Its Applications, 285 (3–4): 539–546, arXiv:cond-mat/0008357, Bibcode:2000PhyA..285..539M, doi:10.1016/s0378-4371(00)00311-3, S2CID 10523345
- ^ Dekker, Anthony (2005). "Conceptual Distance in Social Network Analysis". Journal of Social Structure. 6 (3).
- ^ Yannick Rochat. Closeness centrality extended to unconnected graphs: The harmonic centrality index (PDF). Applications of Social Network Analysis, ASNA 2009.
- ^ Freeman, Linton (1977). "A set of measures of centrality based upon betweenness". Sociometry. 40 (1): 35–41. doi:10.2307/3033543. JSTOR 3033543.
- ^ a b c Brandes, Ulrik (2001). "A faster algorithm for betweenness centrality" (PDF). Journal of Mathematical Sociology. 25 (2): 163–177. CiteSeerX 10.1.1.11.2024. doi:10.1080/0022250x.2001.9990249. hdl:10983/23603. S2CID 13971996. Retrieved October 11, 2011.
- ^ M. E. J. Newman. "The mathematics of networks" (PDF). Retrieved 2006-11-09.
{{cite journal}}:Cite 저널 요구 사항journal=(도움말) - ^ a b "American Mathematical Society".
- ^ M. E. J. Newman. "The mathematics of networks" (PDF). Retrieved 2006-11-09.
{{cite journal}}:Cite 저널 요구 사항journal=(도움말) - ^ 1953년 L. Katz사회 측정 지수에서 파생된 새로운 상태 지수.사이코메트리카, 39~43세
- ^ Bonacich, P (1991). "Simultaneous group and individual centralities". Social Networks. 13 (2): 155–168. doi:10.1016/0378-8733(91)90018-o.
- ^ Google은 웹 페이지의 순위를 어떻게 매깁니까?2012년 1월 31일 Wayback Machine 20Q 아카이브: 네트워크 라이프에 대하여
- ^ Piraveenan, M.; Prokopenko, M.; Hossain, L. (2013). "Percolation Centrality: Quantifying Graph-Theoretic Impact of Nodes during Percolation in Networks". PLOS ONE. 8 (1): e53095. Bibcode:2013PLoSO...853095P. doi:10.1371/journal.pone.0053095. PMC 3551907. PMID 23349699.
- ^ Faghani, Mohamamd Reza (2013). "A Study of XSS Worm Propagation and Detection Mechanisms in Online Social Networks". IEEE Transactions on Information Forensics and Security. 8 (11): 1815–1826. doi:10.1109/TIFS.2013.2280884. S2CID 13587900.
- ^ Alvarez-Socorro, A. J.; Herrera-Almarza, G. C.; González-Díaz, L. A. (2015-11-25). "Eigencentrality based on dissimilarity measures reveals central nodes in complex networks". Scientific Reports. 5: 17095. Bibcode:2015NatSR...517095A. doi:10.1038/srep17095. PMC 4658528. PMID 26603652.
- ^ Alvarez-Socorro, A.J.; Herrera-Almarza; González-Díaz, L. A. "Supplementary Information for Eigencentrality based on dissimilarity measures reveals central nodes in complex networks" (PDF). Nature Publishing Group.
추가 정보
- Koschützki, D.; L., Peeters, L.; Richter, S.; Tenfelde-Podehl, D. 및 Zlotowski, O.(2005) 중심성 지수.미국 브란데스와 텍사스 주 얼바흐(Eds)네트워크 분석: 방법론 기초, 16-61, LNCS 3418, Springer-Verlag.



 보행길이입니다.
보행길이입니다. 변환된 인접관계 매트릭스입니다.
변환된 인접관계 매트릭스입니다. 합계의 수렴을 보장하는 할인 파라미터입니다.
합계의 수렴을 보장하는 할인 파라미터입니다.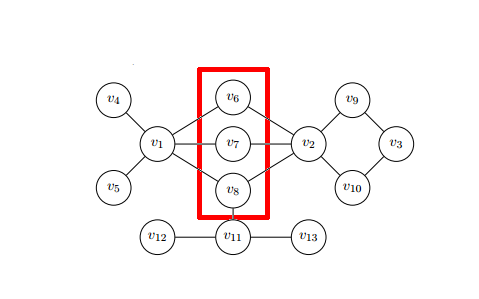




 정점과
정점과



 소요되며, 에지에 대해서는 희박한
소요되며, 에지에 대해서는 희박한  소요됩니다.
소요됩니다. 



 .
.
![H=\sum _{{j=1}}^{{|Y|}}[C_{D}(y*)-C_{D}(y_{j})]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9666585dcf8a4913865d385f3e974c6891c879f3)
![{\displaystyle C_{D}(G)={\frac {\sum _{i=1}^{|V|}[C_{D}(v*)-C_{D}(v_{i})]}{H}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29d1d78ee22a5ca4dbfab56ee81d15d2206300f0)
 최대화됩니다.
최대화됩니다.
![{\displaystyle C_{D}(G)={\frac {\sum _{i=1}^{|V|}[C_{D}(v*)-C_{D}(v_{i})]}{|V|^{2}-3|V|+2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7551bf124c85cb266574ec4aab363a0f9d6eb05c)




 그래프에서 노드 수입니다.
그래프에서 노드 수입니다.
 강한 상관관계가 있다.
강한 상관관계가 있다.  }의 정점과 β}도이다.
}의 정점과 β}도이다. 
 . 고조파 중심성은
. 고조파 중심성은














 v{
v{ 상수입니다.작은 재배열로 이것은 벡터 표기법으로 고유
상수입니다.작은 재배열로 이것은 벡터 표기법으로 고유 


 (
(

 x
x







![PC^t(v)= \frac{1}{N-2}\sum_{s \neq v \neq r}\frac{\sigma_{sr}(v)}{\sigma_{sr}}\frac{{x^t}_s}{{\sum {[{x^t}_i}]}-{x^t}_v}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff9329766cc6f7d93f19d9703dd81488fb14b5e7)

 대한 최단 경로의 총수이며,
대한 최단 경로의 총수이며, 

 침투 상태는
침투 상태는 

 실행되며, 계산에서 목표 노드의 가중치를 고려할 필요가 있는 경우 가장 나쁜 시간은
실행되며, 계산에서 목표 노드의 가중치를 고려할 필요가 있는 경우 가장 나쁜 시간은
 크로스 클리크 연결은
크로스 클리크 연결은


 최대 차이 합계입니다.네트워크의 집중화는 다음과 같습니다.
최대 차이 합계입니다.네트워크의 집중화는 다음과 같습니다.


 임의의
임의의 




