모듈러성(네트워크)

시리즈의 일부
네트워크 과학
이론.
그래프 복잡한 네트워크 전염병 작은 세상 스케일프리 커뮤니티 구조 퍼콜레이션 진화 제어성 그래프 그리기 사회자본 링크 분석 최적화 상호주의 클로즈 호모필리 이동성 우선 첨부 균형 이론 네트워크 효과 사회적 영향
네트워크 타입
정보(컴퓨팅) 전기 통신 운송 사회의 과학적 협업 생물학적 인공 신경 상호의존적 의미론 공간의 의존 흐름 온칩
그래프
특징들 클리크 요소 인하. 사이클 data 구조 엣지 고리 근린 경로. 꼭지점 인접 리스트/매트릭스 발생 목록/매트릭스 종류들 초당파 완성하다 연출된 들뜬 멀티 랜덤 가중치
측정 기준 알고리즘
중앙집중성 도 모티브 클러스터링 학위 분포 구색성 거리 모듈러성 효율성.
모델
토폴로지 랜덤 그래프 에르데스-레니 바라바시-알베르트 비앙코니바라바시 피트니스 모델 와츠 스트로게츠 지수 랜덤(ERGM) 랜덤 지오메트릭(RGG) 쌍곡선(HGN) 계층적 확률 블록 블록 모델링 최대 엔트로피 소프트 컨피규레이션 LFR 벤치마크 다이내믹스 부울 네트워크 에이전트 베이스 전염병/S적외선
리스트 분류
토픽 소프트웨어 네트워크 과학자 카테고리:네트워크 이론 카테고리:그래프 이론
v t

모듈성은 네트워크 또는 그래프의 구조를 측정하는 척도로, 네트워크를 모듈(그룹, 클러스터 또는 커뮤니티라고도 함)로 분할하는 강도를 측정합니다.모듈성이 높은 네트워크는 모듈 내의 노드 간에는 고밀도의 접속이 존재하지만 다른 모듈 내의 노드 간에는 저밀도의 접속이 있습니다.모듈러성은 네트워크의 커뮤니티 구조를 검출하기 위한 최적화 방법으로 자주 사용됩니다.그러나 모듈화는 해결 한계를 겪고, 따라서 작은 커뮤니티를 탐지할 수 없는 것으로 나타났습니다.동물의 뇌를 포함한 생물학적 네트워크는 고도의 모듈성을 보인다.

동기

많은 과학적으로 중요한 문제들은 네트워크를 사용하여 표현되고 경험적으로 연구될 수 있다.예를 들어, 생물학적 및 사회적 패턴, 월드 와이드 웹, 대사 네트워크, 먹이 네트워크, 신경 네트워크 및 병리 네트워크는 수학적으로 표현되고 토폴로지적으로 연구되어 예기치 않은 구조적 ^[1]특징을 드러낼 수 있는 현실 세계의 문제이다.이러한 네트워크의 대부분은 네트워크의 역동성에 관한 이해를 구축하는 데 매우 중요한 특정 커뮤니티 구조를 가지고 있습니다.예를 들어, 밀접하게 연결된 사회 공동체는 느슨하게 연결된 사회보다 그들 사이의 정보나 루머의 빠른 전송 속도를 의미할 것이다.따라서 네트워크가 링크에 의해 접속된 다수의 개별 노드에 의해 표현되어 노드 간의 어느 정도의 상호작용을 나타내는 경우, 커뮤니티는 네트워크의 나머지 부분과 희박하게 접속되어 있는 조밀하게 상호 접속된 노드의 그룹으로 정의됩니다.따라서 커뮤니티는 노드 정도, 클러스터링 계수, 간성, 중앙 ^[2]집중성 등의 특성이 상당히 다를 수 있으므로 네트워크 내의 커뮤니티를 식별하는 것이 필수적일 수 있습니다.등입니다.모듈화는 이러한 척도의 하나로, 최대화하면 특정 네트워크 내에 커뮤니티가 출현합니다.

정의.

모듈성은 주어진 그룹에 속하는 가장자리에서 가장자리가 랜덤하게 분포된 경우 예상되는 분율을 뺀 값입니다.무가중 및 무방향 그래프의 모듈성 값은${\displaystyle }$[${\displaystyle }$-${\displaystyle 1}$ /${\displaystyle 2\mathrm{}}$ , $]$ {$display$[ -$1$ / $2$, 1$\}$^[3] 범위에 있습니다.그룹 내 에지 수가 예상 수를 초과하면 양수입니다.일부 모듈로 네트워크 정점의 주어진 분할에 대해, 모듈화는 모듈에 관계없이 모든 노드 사이의 링크의 랜덤 분포와 비교하여 모듈 내의 에지 집중도를 반영한다.

모듈성을 ^[1]계산하는 방법에는 여러 가지가 있습니다.이 개념의 가장 일반적인 버전에서는 각 정점의 정도를 유지하기 위해 에지의 랜덤화가 이루어진다.$멤버십$$$변수 $s$를 $사용$하여 그래프를 2개의 $커뮤니티$로 분할할 수 있도록 n개의 $노드$ 및 m개의$$ 링크(표시 스타일$)$를 $가진{\displaystyle }$그래프를 검토합니다.$노드{\displaystyle }$ v가$$ 커뮤니티 $1$에 ${\displaystyle \mathrm{속해}}$ ${\displaystyle {있는}_{}}$ 경우 s v$$${\displaystyle {}_{}}$1 {$display$ $style$ $s_{v$}=1}, 또는 v$${\display style$$s_$\{$v$}$ $=$1}, $또는$ v {\display}의 $경우{\displaystyle }$,$style$ v$}$는 $커뮤니티{\displaystyle {}_{}}$ 2, s ${\displaystyle v_{}}$ $=$ -$$ {\$displaystyle s_{v$}=-$1$에 속합니다. ${\displaystyle {네트워크}_{}}$의 인접 행렬을 $A{\displaystyle }${$style$ A$$}로$$나타냅니다. $여기$서 A v w = 0 {displaystyle $A_{vw$$}$ $= 0$은 노드$$$vstyle$ $v$와$$$wstyle$vstyle ${\displaystyle {사이}_{}}$에 에지(상호작용 없음)가 없음을 의미합니다.${\displaystyle {}_{}}$w $=$ $(\displaystyle A_{vw$}=$1)$은 둘 사이에 가장자리가 있음을 의미합니다.또, 심플화를 위해서, 무방향 네트워크를 고려하고 있습니다.${\displaystyle {따라서}_{}}$ A ${\displaystyle v_{}}$ w ${\displaystyle {}_{}}$ ${\displaystyle A_{}}$w ${\displaystyle w_{}}$ \ $displaystyle A_{vw$} $=$$A_{wv$ (두 노드 사이에 여러 개의 가장자리가 존재할 수 있다는 점에 유의해야 합니다만, 여기서는 가장 단순한 경우를 평가합니다.)

다음으로 $모듈성{\displaystyle }$Q(\$displaystyle$ Q$)$는 그룹 1 또는 2에 속하는 에지의 분율에서 지정된 네트워크와 동일한 노드도 분포를 갖는 랜덤 그래프에 대해 그룹 1 및 2 내의 예상 에지 수를 뺀 값으로 정의됩니다.

예상되는 가장자리 수는 구성 ^[4]모델의 개념을 사용하여 계산해야 합니다.설정 모델은 특정 네트워크를 랜덤하게 실현하는 것입니다.n개의$노드$를 $가진{\displaystyle }$ 네트워크$($각 $노드{\displaystyle }$ v의 노드 ${\displaystyle {도수}_{}}$ k$({$$$k_$$${v$에서는 구성 모델은 각 에지를 2등분하여 스터브라고 불리는 각 하프 엣지를 네트워크 내의 다른 스탭과 랜덤하게 재배선하여 셀프루프도 가능하게 합니다.stub이 같은 노드에서 다른 stub으로 재배선되어 같은2개의 노드간에 멀티패킷이 배치됩니다.따라서 그래프의 노드도 분포는 그대로 유지되지만 설정 모델에서는 완전히 랜덤네트워크가 생성됩니다.

노드 간 예상 에지 수

이제 위에서 설명한 대로 무작위로 재배선된 네트워크로부터의 노드 $도수$가 ${\displaystyle {각각}_{}}$ k$({$와 $({$인 2개의 $노드{\displaystyle }$v(\$displaystyle$ v$)$와 w$(\displaystyle$ w$)$에 대해 살펴보겠습니다.이러한 노드 사이의 예상되는 최대 에지 수를 계산합니다.

$v$의 $k{\displaystyle {}_{}}$ ${\displaystyle v_{}}${\$style$$$$k_{v}$ stub을$$ 각각 고려하여 ${\displaystyle i_{}^{}}$${\displaystyle {}_{}^{}}$(${\displaystyle v_{}^{}}$${\displaystyle {}_{}^{}}$,${\displaystyle {}_{}^{}}$w$$){$display I_{i}^{(v$,$w)}$에 대해 i ${\displaystyle =}$ ${\displaystyle 1}$, ${\displaystyle ...}$ , k$$ { $display i$${\displaystyle {}_{}^{}}$$1$, \$ldots ,$${\displaystyle {\mathrm{k\_v}}_{}^{}}$$\}$ 를 $작성$합니다${\displaystyle {.}_{}^{}}$$이$$랜덤 그래프$에서 $i번째{\displaystyle }$ $스터브$가 $노드{\displaystyle }$$w의$k w stub$$ 중 $하나$에 연결되어 있는 경우$.$그렇지 않은 ${\displaystyle {경우}_I^{}}$( ${\displaystyle v_{}^{}}$, w ) $=$ ${\displaystyle 0}$ { { $displaystyle$ I _ { $i$}^{ ($v$ , w ) =$0$} 。$node{\displaystyle }$v { \ $displaystyle$ v$$ $}$의 i$${ $style$ i$$} - stub은 2${\displaystyle }$m -$$ { $display$2 ${\displaystyle m}$ -$$1 }의$$ $나머지{\displaystyle \mathrm{}}$ stub에 동등한 확률로 접속할 수 있기 $때문에 kw${\ style k_w$}$이 있습니다.$노드{\displaystyle }$ w$\displaystyle$w에 관련지어져 있습니다.

${\displaystyle p(I_{i}^{(v,w)}=1)=E[I_{i}^{(v,w)}]=param frac {k_{w}}{2m-1}}$

v$${$displaystyle$ v$}$와$$w {$displaystyle$ $w$$}$ 사이의$$ 풀 $에지{\displaystyle }$ ${\displaystyle J_{}}$ $v{\displaystyle {}_{}}$ w ${$의 총 수는 J ${\displaystyle v_{}}$ ${\displaystyle w_{}}$ ${\displaystyle {}_{}\underset{\mathrm{i}}{\overset{}{}}}$ i ${\displaystyle \underset{}{\overset{}{=}}}$ 1 ${\displaystyle \underset{}{\overset{}{{}_{}}}}$ ${\displaystyle \underset{}{\overset{}{v_{}}}}$ ${\displaystyle I_{}^{}}$( ${\displaystyle v_{}^{}}$,${\displaystyle w_{}^{}}$) \ $displaystyle J_{vw$= \ $sum$_ { i$$=$1$}^$k_${v$}$ 입니다.$I_{i}^{(v,w$ 따라서 이 수량의 예상값은 다음과 같습니다.

$\displaystyle E[J_{vw}]=E\left[\sum _{i=1}^{k_{v}}I_{i}^{(v,w)}\right]=\sum _{i=1}^{k_{v}}E[I_{i}^{(v,w)}=\sum _{i=1}^{k_{v}}{\frac {k_{w}}{2m-1}=flac {k_{v}k_{w}}}{2m-1}}}$

그런 다음 많은 텍스트가 에지의 수가 많은 랜덤 네트워크에 대해 다음과 같은 근사치를 만듭니다.m$(\displaystyle$ m$)$이 클 $경우{\displaystyle }$ 위의 분모에 1$(\displaystyle$1)을 빼고 단순히 두 노드 사이의 예상 에지 수에 대한 $근사식{\displaystyle \frac{{}_{}}{}}$ ${\displaystyle \frac{k_{}}{}}$ v ${\displaystyle \frac{k_{}}{}}$ ${\displaystyle \frac{{}_{}}{\mathrm{}}}$ 2$$(\$display$style ${k_{v}k_{w}})$을 사용합니다.게다가 대규모 랜덤 네트워크에서는, 셀프 루프와 멀티 에지의 수는 지극히 ^[5]적어집니다.셀프루프 및 멀티에지를 무시하면 2개의 노드 사이에 최대 1개의 엣지가 있다고 가정할 수 있습니다.이 경우 ${\displaystyle J_{}}$ v ${\displaystyle w_{}}${ $display J$_ { $vw$} $becomes$ indicator variable variable variable variable variable variable variable variable variable variable variable variable variable variable variable variable variable variable variable variable variable variable인디케이터 변수가 되므로 기대치도$$1 { $displaystyle$1 $\}$이 될 가능성이 있습니다.$즉{\displaystyle }$, 노드$$v { $displaystyle$$$v}와$$w$사이$에 엣지가 존재할 확률을 ${\displaystyle \frac{{}_{}{}_{}}{}}$ ${\displaystyle \frac{k_{}}{}}$ ${\displaystyle \frac{w_{}}{}}$로 추정할 수 있습니다.${\displaystyle \frac{}{2}}$m (\ $displaystyle$\$frac${ $k _$ {$v }$ k _ { w } ){ 2 $m$} $。$

모듈러성

$따라서{\displaystyle }$ 노드$v$와 $\displaystyle$w 사이의$$ 실제 에지 수와 이들 사이의 예상되는 에지 수는 다음과 같습니다.

${\displaystyle A_{vw}-{\frac {k_{v}k_{w}}{2m}}$

모든 노드 쌍을 합산하면 모듈화 Q$(\displaystyle$ Q$)$^[1]라는 $방정식$이 나타납니다.

${\displaystyle Q=flac {1}{2m}}\sum _{vw}\left[A_{vw}-{\frac {k_{v}k_{w}}{2m}\right]{\frac {s_{v}s_{w}+1}{2}}}}$

(3)

Eq.3은 2개의 커뮤니티로 분할하는 경우에만 유효합니다.계층적 분할(즉, 두 개의 커뮤니티로 분할한 후 Q를 최대화하기 위해 두 개의 작은 서브 커뮤니티로 더 분할한 두 개의 서브 커뮤니티)은 네트워크 내의 여러 커뮤니티를 식별하는 가능한 접근법입니다.또, (3)은,^[6] 네트워크를 c커뮤니티로 분할하기 위해서 일반화 할 수 있다.

${\displaystyle Q=flac {1}{(2m)}}\sum _{vw}\left[A_{vw}-{\frac {k_{v}k_{w}}{(2m)}}\right]\sum (c_{v},c_{w}=\sum _{i=1}^c}(e_{i}-a_{i}^2})$

(4)

여기서_ij e는 커뮤니티 i의 한쪽 끝 정점과 커뮤니티 j의 다른 한쪽 끝 정점이 있는 가장자리 비율입니다.

${displaystyle e_{ij}=\sum _{vw}{\frac {A_{vw}}{2m}}1_{v\in c_{i}}1_{w\in c_{j}}}}$

a는_i 커뮤니티 i의 정점에 부착된 가장자리 끝의 비율입니다.

$({displaystyle a_{i}=sum frac {k_{i}}{2m}=\sum _{j}e_{ij})$

멀티 커뮤니티 검출의 예

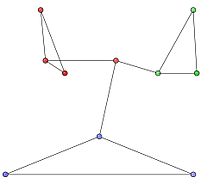
10개의 노드와 12개의 엣지를 가진 무방향 네트워크 및 다음 인접 매트릭스를 고려합니다.

노드 ID	1	2	3	4	5	6	7	8	9	10
1	0	1	1	0	0	0	0	0	0	1
2	1	0	1	0	0	0	0	0	0	0
3	1	1	0	0	0	0	0	0	0	0
4	0	0	0	0	1	1	0	0	0	1
5	0	0	0	1	0	1	0	0	0	0
6	0	0	0	1	1	0	0	0	0	0
7	0	0	0	0	0	0	0	1	1	1
8	0	0	0	0	0	0	1	0	1	0
9	0	0	0	0	0	0	1	1	0	0
10	1	0	0	1	0	0	1	0	0	0

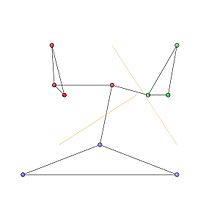
그래프 내의 커뮤니티는 그림 1의 빨간색, 녹색 및 파란색 노드 클러스터로 나타납니다.최적의 커뮤니티 파티션은 그림 2와 같다.

행렬 공식화

특히 스펙트럼 최적화 알고리즘에서 유용한 모듈화의 대체 공식은 다음과 같다.^[1]$정점{\displaystyle }$v(\$displaystyle$ v$)$가 $그룹{\displaystyle }$r(\$displaystyle$ r$)$에 속하면 S v r(\$displaystyle S_{vr})$을 1$(\displaystyle$ 1$)$로 정의하고, $그렇지{\displaystyle \mathrm{}}$ 않으면 0$(\displaystyle$ 0$)$으로 $정의$합니다.그리고나서

$\displaystyle \displaystyle (c_{v,c_{w})=\sum _{r}S_{vr}S_{wr}$

그렇기 때문에

${\displaystyle Q=flac {1}{2m}}\sum _{vw}\sum _{r}\left[A_{vw}-{\frac {k_{v}k_{w}}{2m}}\right]S_{vr}S_{wr}=paramfrac {1}{2m}}\mathrm {Tr}(\mathbf {S}^{\mathrm {T}}\mathbf {BS}),$

$여기$서 S$(\displaystyle$ S$)$는 $요소{\displaystyle {}_{}}$ $(\$를 갖는 (비사각형) $매트릭스$이며$,$ B(\$displaystyle$ B$)$는 요소를 갖는 모듈러 매트릭스입니다.

${\displaystyle B_{vw}=A_{vw}-{\frac {k_{v}k_{w}}{2m}}.}$

모듈러성 매트릭스의 모든 행과 열의 합계는 0이 됩니다.즉, 분할되지 않은 네트워크의 모듈러성도 $항상{\displaystyle \mathrm{}}$ 0$(\displaystyle$ 0$)$임을 의미합니다.

2개의 커뮤니티만으로 분할된 네트워크의 경우 노드$v$가 속한 커뮤니티를 나타내기 위해 s ${\displaystyle v_{}}$ $=$ ±$$(\$displaystyle$ $s_{v$}=\$pm$1)을$$ $정의$할 수 있습니다.이것에 의해$,$ 다음과 같이 됩니다.

${\displaystyle Q={1 \over 4m}\sum _{vw}B_{v}s_{w}={1 \over 4m}\mathbf {s}^{\mathrm {T}}\mathbf {Bs},}$

$여기$서 s$${\$displaystyle$s$}$는 요소$$ s {\$displaystyle$ s_$\{$^[1]$v}}$가 있는 열 벡터입니다.

이 함수는 Ising 스핀 글라스의 Hamiltonian과 동일한 형태를 갖습니다.이것은 예를 들어 모듈성을 최대화하기 위해 간단한 컴퓨터 알고리즘을 작성하기 위해 이용된 연결입니다.임의의 수의 커뮤니티에 대한 모듈화의 일반적인 형태는 포츠 스핀 글라스와 동일하며, 이 경우에도 ^[7]유사한 알고리즘을 개발할 수 있습니다.

해상도 제한

모듈성은 클러스터 내의 에지 수와 네트워크가 노드 수가 같고 각 노드가 그 정도를 유지하는 랜덤 네트워크일 경우 클러스터에서 발견되는 예상 에지 수를 비교합니다. 그러나 그 이외의 경우에는 에지가 랜덤하게 연결됩니다.이 랜덤 늘모델에서는 각 노드가 네트워크의 다른 노드에 접속할 수 있다고 암묵적으로 가정하고 있습니다.그러나 네트워크의 규모가 매우 큰 경우 노드의 호라이즌에는 네트워크의 작은 부분이 포함되어 대부분의 노드를 무시하기 때문에 이 가정은 타당하지 않습니다.게다가 이것은, 네트워크의 사이즈가 증가하면, 2개의 노드 그룹간의 예상 에지수가 감소하는 것을 의미합니다.따라서, 네트워크가 충분히 큰 경우, 모듈러 모델의 null 모델에 있는 두 노드 그룹 사이의 예상되는 에지 수는 1보다 적을 수 있습니다.이 경우 두 클러스터 간의 단일 가장자리는 모듈화로 해석되어 두 클러스터 간의 강력한 상관관계를 나타내는 신호로 해석됩니다. 모듈성을 최적화하면 클러스터의 기능과 독립적으로 두 클러스터가 병합됩니다.따라서 내부 에지의 밀도가 가장 높고 식별 가능한 최고의 커뮤니티를 나타내는 약하게 상호 연결된 완전 그래프도 네트워크가 충분히 ^[8]크면 모듈러성 최적화에 의해 병합된다.이러한 이유로 대규모 네트워크에서 모듈화를 최적화하면 소규모 커뮤니티가 잘 정의되어 있어도 해결할 수 없습니다.이러한 편향은 글로벌 늘 ^[9]모델에 의존하는 모듈러 최적화와 같은 방법에서 불가피합니다.

멀티레졸루션 방식

한 self-loop의(r<0)집단이 형성되기(r>0)거나 줄어드노드의 혐오감을 향상시키는 형태에서 모듈화 컨텍스트 내에서 해상 한계 해결하기 위해 두 중요한 접근 방식:저항 r의 모든 노드에,[10]또는 매개 변수 γ&gt의 추가;0은 defin의null-case 용어 앞에 있다.modu의 itionlarity: 커뮤니티 내부 링크와 눌모델 ^[7]간의 상대적 중요도를 제어합니다.각각의 적절한 범위에서 이들 파라미터의 값에 대한 모듈성을 최적화함으로써 네트워크의 전체 메소스케일을 모든 노드가 동일한 커뮤니티에 속하는 매크로스케일에서 각 노드가 자체 커뮤니티를 형성하는 마이크로스케일, 즉 멀티레졸루션 방식이라는 이름으로 회복할 수 있다.그러나 커뮤니티의 ^[11]크기가 매우 이질적인 경우에는 이러한 방법에는 한계가 있는 것으로 나타났다.

소프트웨어 도구

모듈러성이 뛰어난 그래프로 클러스터링을 계산할 수 있는 몇 가지 소프트웨어 도구가 있습니다.

멀티 레벨 Louvain 메서드의 ^[12]최초 구현.

접속되어 있지 ^[13]않은 커뮤니티를 추가로 회피하는 레이든 알고리즘.

Vienna Graph Clustering(VieClus) 알고리즘, 병렬 메모리 알고리즘.^[14]

「 」를 참조해 주세요.

• 복잡한 네트워크
• 커뮤니티 구조
• Null 모델
• 침투 이론

레퍼런스