바라바시-알베르트 모형

시리즈의 일부
네트워크 과학
이론.
그래프 복합망 전염 소세계 스케일 프리 커뮤니티 구조 퍼콜레이션 진화 제어가능성 그래프도면 사회적 자본 링크분석 최적화 호혜성 폐쇄 호모필리 감수성 우선첨부 균형이론 네트워크 효과 사회적 영향
네트워크 유형
정보(컴퓨팅) 텔레커뮤니케이션 운송 사회의 과학적 협업 생물학적 인공신경 상호의존적 시맨틱 공간의 의존 흐름 온칩의
그래프
특징들 클리크 요소 인하. 사이클 자료구조 가장자리 고리 이웃 경로. 꼭짓점 인접 목록 / 행렬 발생목록/행렬 종류들 초당파 완성하다 연출된 들뜬 라벨링 멀티 랜덤 가중
메트릭 알고리즘
중심성 도 모티프 클러스터링 정도분포 구색성 거리 모듈화 효율성.
모델들
위상 랜덤그래프 에르트 ő스 - 레니 바라바시-알베르트 비앙코니 바라바시 피트니스 모델 와츠-스트로가츠 지수난수(ERGM) 랜덤 기하학(RGG) 쌍곡선(HGN) 계층적 확률적 블록 블록모델링 최대 엔트로피 소프트 구성 LFR 벤치마크 역학 부울 네트워크 대리인 기반의 전염병/SIR
목록 분류
토픽 소프트웨어 네트워크 과학자 카테고리:네트워크 이론 카테고리:그래프이론
v t

BA(Barabási–Albert) 모델은 우선 부착 메커니즘을 사용하여 랜덤 스케일 프리 네트워크를 생성하는 알고리즘입니다. 인터넷, 월드 와이드 웹, 인용 네트워크 및 일부 소셜 네트워크를 포함한 여러 자연 및 인간이 만든 시스템은 거의 규모가 없는 것으로 간주되며 네트워크의 다른 노드에 비해 비정상적으로 높은 수준의 노드(허브라고 함)가 거의 포함되지 않습니다. BA 모델은 실제 네트워크에서 이러한 노드의 존재를 설명하려고 합니다. 이 알고리즘의 이름은 발명가인 Albert-László Barabasi와 Réka Albert의 이름을 따서 지어졌습니다.

컨셉트

관측된 많은 네트워크(적어도 대략)는 규모 없는 네트워크 클래스에 속하며, 이는 멱법칙(또는 규모가 없는) 정도 분포를 가지고 있는 반면, Erd ős–Rennyi(ER) 모델 및 Watts–Strogatz(WS) 모델과 같은 무작위 그래프 모델은 멱법칙을 나타내지 않습니다. Barabási-Albert 모델은 스케일 프리 네트워크를 생성하는 여러 제안 모델 중 하나입니다. 성장과 우선 애착이라는 두 가지 중요한 일반 개념을 통합합니다. 성장과 우대 애착 모두 실제 네트워크에 널리 존재합니다.

성장은 네트워크의 노드 수가 시간이 지남에 따라 증가한다는 것을 의미합니다.

우선 연결은 노드가 연결되어 있을수록 새 링크를 받을 가능성이 높다는 것을 의미합니다. 정도가 높은 노드는 네트워크에 추가된 링크를 더 잘 파악할 수 있습니다. 직관적으로 사람들을 연결하는 소셜 네트워크 측면에서 생각해보면 특혜 애착을 이해할 수 있습니다. 여기서 A에서 B로의 링크는 A가 B를 "안다"거나 "안다"는 것을 의미합니다. 많이 연결된 노드는 많은 관계를 가진 잘 알려진 사람들을 나타냅니다. 새로운 사람이 지역 사회에 들어올 때, 그들은 상대적으로 알려지지 않은 사람들보다 더 눈에 보이는 사람들 중 한 명과 친해질 가능성이 더 높습니다. BA 모델은 월드 와이드 웹에서 새로운 페이지는 거의 아무도 모르는 페이지가 아니라 허브, 즉 구글과 같은 매우 잘 알려진 사이트로 우선적으로 링크된다고 가정하여 제안되었습니다. 기존 링크를 임의로 선택하여 링크할 새 페이지를 선택할 경우 특정 페이지를 선택할 확률은 그 정도에 비례합니다. BA 모델은 이것이 우선 부착 확률 규칙을 설명한다고 주장합니다.

나중에 Bianconi-Barabási 모델은 "적합성" 매개변수를 도입하여 이 문제를 해결합니다. 우선 첨부는 초기 랜덤 변동(한 노드에 처음에 더 많은 링크가 있거나 다른 노드보다 먼저 링크를 축적하기 시작한 노드)이 자동으로 강화되어 차이가 크게 확대되는 긍정적인 피드백 주기의 예입니다. 이것은 때때로 "부자는 더 부자가 된다"는 매튜 효과라고도 불립니다. 자기 촉매 작용도 참조하십시오.

알고리즘.

BA 모델의 유일한 매개 변수는 양의$$$정수$인 m$${\$displaystyle$ m$}$입니다. 네트워크는 $m0$≥ m ${\displaystyle m_{$0}\geq m} 노드의 네트워크로 초기화됩니다.

각 단계에서 하나의 새 노드를 추가한 다음 기존 노드가 이미 가지고 있는 링크 수에 비례하는 확률로 $네트워크$에서 m ${\displaystyle$ m$}$개의$$ 기존 정점을 샘플링합니다(원제 논문에서는 동일한 기존 노드를 여러 번 선택하는 경우의 처리 방법을 지정하지 않았습니다). 형식적으로 새 노드가 노드 $i{\displaystyle }$ ${\$$displaystyle$ $p_$${i}$에 연결될$$ 확률 ${\displaystyle {pi}_{}}$ ${\$$displaystyle$ i$}$는^[1]

${\displaystyle p_{i}={\frac {k_{i}}{\sum _{j}k_{j}}},}$

여기서 ${\displaystyle {ki}_{}}$ ${\$는 $노드{\displaystyle }$ i ${\displaystyle i}$의 정도이며, 합은 모든 기존 $노드{\displaystyle }$ j$${\$displaystyle$ j$}$에 대해 이루어집니다(즉, 분모는 네트워크의 현재 에지 수의 두 배가 됩니다).$$ 이 단계는 먼저 하나의 에지를 균일하게 샘플링한 다음 에지의 두 정점 중 하나를 샘플링하여 수행할 수 있습니다.

링크가 많이 연결된 노드("허브")는 빠르게 더 많은 링크를 축적하는 경향이 있는 반면, 링크가 몇 개만 있는 노드는 새로운 링크의 대상으로 선택될 가능성이 거의 없습니다. 새로운 노드는 이미 많이 연결된 노드에 자신을 연결하는 "선호"를 가지고 있습니다.

특성.

정도분포

BA 모델의 결과로 나타나는 정도 분포는 척도가 없으며, 특히 형태의 거듭제곱 법칙입니다.

${\displaystyle P(k)\simk^{-3}\,}$

허쉬지수분포

h-지수 또는 Hirsch 지수 분포도 척도가 없는 것으로 나타났으며 중심성 측도로^[2] 사용하기 위해 로비 지수로 제안되었습니다.

${\displaystyle H(k)\simk^{-6}\,}$

$또한$ m ${\displaystyle 0_{}}$ = ${\$displaystyle m_{0} = $1}$인 경우 h-index 1인 노드의 밀도에 대한 분석 결과를 얻을 수 있습니다.

${\displaystyle H(1){\Big }_{m_{0}=1}=4-\pi \,}$

노드 차수 상관 관계

연결된 노드의 정도 사이의 상관 관계는 네트워크가 진화하는 방식 때문에 BA 모델에서 자발적으로 발전합니다. ${\displaystyle n_{}}$$$k$$ℓ${\displaystyle$ $n_{$k$\backslash$ell}}, m = 1 {\displaystyle m=1}(BA 트리)의 $특수$한 경우에$$대한 BA 모델에서 {\$displaystyle$ k}의$$노드를 ${\displaystyle$ \ell}의 조상$$노드에 연결하는 링크를 찾을 확률은 다음과 같습니다.

${\displaystyle n_{k\ell} = {\frac {4\left(\ell -1\right)}{k\left(k+1\right)\left(k+\ell \right)\left(k+\ell +1\right)\left(k+\ell +2\right)}}+{\frac {12\left(\ell -1\right)}{k\left(k+\ell -1\right)\left(k+\ell \right)\left(k+\ell +1\right)\left(k+\ell +2\right)}}.$

이것은 분포가 상관이 $없는$ 경우 n ${\displaystyle k_{}{}^{}}$ℓ =$$k - 3 ℓ - 3 ${\displaystyle$ n_{k\$ell$} = k^{-3}\ell ^{-3}}을 얻기 때문에 정도 상관이 있음을 확인합니다.

$일반적$인 m ${\displaystyle$ m$}$의 경우 ${\displaystyle$ k$} 정도$의 노드를$$ℓ {\displaystyle$$\ell} 정도의 노드에 연결하는 링크의 비율은 다음과 같습니다.

${\displaystyle p(k,\ell )={\frac {2m(m+1)}{k(k+1)\ell (\ell +1)}}\left[1-{\frac {{\binom {2m+2}{m+1}}{\binom {k+\ell -2m}{\ell -m}}}{\binom {k+\ell +2}{\ell +1}}}\right].}$

또한 가장 가까운 이웃의 차수 $분포$ p${\displaystyle (}$ℓ ∣$$k) {\displaystyle p(\ell \mid k)} 즉, 차수 k가 {\displaystyle k}인 노드의 이웃의 차수 분포는 다음과 같습니다.

${\displaystyle p(\ell \mid k)={\frac {m(k+2)}{k\ell (\ell +1)}}\left[1-{\frac {{\binom {2m+2}{m+1}}{\binom {k+\ell -2m}{\ell -m}}}{\binom {k+\ell +2}{\ell +1}}}\right].}$

즉, 차수 k가 ${\displaystyle$ k$}$인 노드를 선택한$$다음 그 인접 노드 중 하나를 무작위로 선택하면 이 무작위로 선택된 인접 노드가 차수$$ℓ {\displaystyle$$\ell }를 가질 확률은${\displaystyle }$위의 p$($ℓ k)${\displaystyle$ p(\ell k)}${\displaystyle 식을}$ 통해 제공됩니다.

군집계수

BA 모델의 군집화 계수에 대한 분석 결과는 Klemm and Eguíluz에^[4] 의해 얻어졌고 Bollobás에 의해 증명되었습니다.^[5] 군집화 계수를 연구하기 위한 평균 필드 접근법은 Frontzak, Frontczak 및 Holyst에 의해 적용되었습니다.^[6]

이러한 동작은 클러스터링이 시스템 크기와 무관한 소규모 네트워크의 동작과는 여전히 구별됩니다. 계층적 네트워크의 경우, 노드 차수의 함수로서 클러스터링도 멱법칙을 따르며,

${\displaystyle C(k)=k^{-1}.\,}$

이 결과는 Dorogovtsev, Goltsev 및 Mendes에 의해 분석적으로 얻어졌습니다.^[7]

스펙트럼 특성

BA 모델의 스펙트럼 밀도는 랜덤 그래프의 반원형 스펙트럼 밀도와는 다른 형태를 가지고 있습니다. 꼭대기가 반원 위에 잘 놓여 있고 모서리가 멱법칙처럼 붕괴된 삼각형 모양을 하고 있습니다.^[8] (5.1절)에서는 스펙트럼 밀도의 모멘트를 거듭제곱 법칙 지수의 함수로 분석하여 이 스펙트럼 밀도의 형태가 정확한 삼각 함수가 아님을 증명했습니다.

동적 스케일링

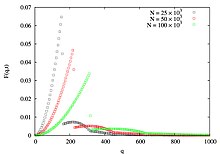
정의에 따라 BA 모델은 시간이 발전하는 현상을 설명하므로 스케일이 없는 특성 외에도 동적 스케일링 특성도 찾을 수 있습니다. BA 네트워크 노드는 또한 BA 네트워크에서 출생 시점이 중요하기 때문에 $k{\displaystyle }$ ${\displaystyle$ k$}$만$$사용하는 대신 각 노드의 출생 시점의 제곱근과 해당하는 $정도{\displaystyle }$ k$${\$displaystyle k$}의$$곱인 일반화된 $정도{\displaystyle }$ q$${\$displaystyle q}$를 특징으로 할 수 있습니다. 일반화된 차수 $분포{\displaystyle }$ F${\displaystyle (q,}$ ${\displaystyle t)}$ ${\displaystyle$ F$(q, t)}$는 사소한 특징이 있으며 동적 스케일링을 나타냄을 발견했습니다.

${\displaystyle F(q,t)\sim t^{-1/2}\phi (q/t^{1/2}).}$

It implies that the distinct plots of ${\displaystyle F(q,t)}$ vs ${\displaystyle q}$ would collapse into a universal curve if we plot ${\displaystyle F(q,t)t^{1/2}}$ vs ${\displaystyle q/t^{1/2}}$.^[10]

제한적인 경우

모델 A

모델 A는 성장은 유지하지만 우선 부착은 포함하지 않습니다. 새 노드가 기존 노드에 연결될 확률은 동일합니다. 이 한계에서 결과적인 정도 분포는 ^[11]기하학적이므로 성장만으로는 규모가 없는 구조를 만들기에 충분하지 않음을 나타냅니다.

모델 B

모델 B는 우선적인 부착은 유지하지만 성장은 제거합니다. 모델은 연결이 끊어진 노드의 고정된 개수로 시작하여 링크를 추가하여 링크 대상으로 높은 차수의 노드를 우선적으로 선택합니다. 시뮬레이션 초기의 정도 분포는 척도가 없어 보이지만 분포가 안정적이지 않으며 결국 네트워크가 포화 상태에 가까워질수록 거의 가우시안이 됩니다. 그래서 우선적인 부착만으로는 규모가 없는 구조를 만들기에 충분하지 않습니다.

모델 A와 B가 척도 없는 분포로 이어지지 못하는 것은 실제 네트워크에서 관찰되는 고정된 멱법칙 분포를 재현하기 위해 성장과 우선적인 부착이 동시에 필요하다는 것을 나타냅니다.^[1]

비선형우선첨부

BA 모델은 보다 일반적인 비선형 우선 부착(NLPA)^[12] 모델의 구체적인 경우로 생각할 수 있습니다. NLPA 알고리즘은 부착 확률이 더 일반적인 형태로 대체된 BA 모델과 동일합니다.

${\displaystyle p_{i}={\frac {k_{i}^{\alpha}}}{\sum _{j}k_{j}^{\alpha}}}$

여기서 $\alpha {\displaystyle }$ ${\displaystyle \alpha}$는 상수 양의 지수입니다. $\alpha$ = ${\$displaystyle \alpha = 1}인 경우 NLPA는 BA 모델로 축소되며 "선형"이라고 합니다. < < ${\displaystyle 0<\alpha <1$인 경우 NLPA는 "서브-선형"이라고 하며 네트워크의 정도 분포는 지수 분포가 늘어나는 경향이 있습니다. > ${\displaystyle \alpha$> $1}$인 경우NLPA는 "초선형"이라고 하며 소수의 노드가 네트워크의 거의 모든 다른 노드에 연결됩니다. < ${\displaystyle \alpha$< $1}$ 및 α> ${\displaystyle \alpha$> $1}$에 대해 네트워크의 스케일 프리 속성은 무한 시스템 크기의 한계로 깨집니다 그러나 $\alpha {\displaystyle }$ ${\displaystyle \alpha}$가 $1{\displaystyle \mathrm{}}$ ${\displaystyle$ 1$}$보다 약간만 큰 경우 NLPA는 일시적으로 스케일이 자유로워 보이는 정도 분포를 초래할 수 있습니다$.$^[13]

역사

우선 부착은 1923년 헝가리 수학자 요르지 폴랴의 유명한 유골함 모델에 처음 등장했습니다.^[14] Herbert A는 좀 더 투명한 유도를 산출하는 마스터 방정식 방법을 문제에 적용했습니다. 1955년^[15] 사이먼은 도시의 크기와 다른 현상들을 연구하는 과정에서. 1976년 Derek de Solla Price에 의해 인용 빈도를 설명하기 위해 처음으로 적용되었습니다.^[16] Price는 과학 논문의 인용 누적에 관심이 있었고 Price 모델은 "누적 우위"(우선적인 부착을 위한 그의 이름)를 사용하여 뚱뚱한 꼬리 분포를 생성했습니다. 현대 인용 네트워크의 언어에서 프라이스의 모델은 지시된 네트워크, 즉 Barabási-Albert 모델의 버전을 생성합니다. "우선 첨부"라는 이름과 현재 스케일 프리 네트워크 모델의 인기는 Albert-László Barabasi와 Réka Albert의 연구에서 기인합니다. 그는 실제 네트워크에 유사한 프로세스가 존재한다는 것을 발견하고 1999년 웹에서 수치적으로 관찰된 정도 분포를 설명하기 위해 우선 첨부를 적용했습니다.^[17]

참고 항목

• 비앙코니-바라바시 모형
• 중식당과정
• 복잡한 네트워크
• Erdős–Rényi (ER) model
• 프라이스의 모델
• 퍼콜레이션 이론
• 스케일 프리 네트워크
• 소규모 네트워크
• 와츠 및 스트로가츠 모델

참고문헌

외부 링크

• "이 사람은 세상을 지배할 수 있었습니다"
• "바라바시 – 알베르트를 위한 자바 구현"
• "Barabási–Albert 모형 그래프를 코드로 생성"