회로 토폴로지(전기)

전자 회로의 토폴로지는 회로 구성 요소의 상호 연결 네트워크에 의해 형성되는 형태입니다.성분의 특정 값 또는 등급이 서로 다른 것은 동일한 토폴로지로 간주됩니다.토폴로지는 회로 내 구성 요소의 물리적 레이아웃이나 회로 다이어그램 상의 위치와는 관련이 없습니다. 토폴로지의 수학적 개념과 유사하게 구성 요소 간에 어떤 연결이 존재하는지에만 관련이 있습니다.동일한 토폴로지에 해당하는 수많은 물리적 레이아웃 및 회로 다이어그램이 있을 수 있습니다.

엄밀히 말하면, 구성 요소를 완전히 다른 유형으로 교체하는 것은 여전히 동일한 토폴로지입니다.그러나 일부 상황에서는 다른 토폴로지로 대략 설명할 수 있습니다.예를 들어, 저역 통과 필터에서 인덕터와 커패시터를 교환하면 고역 통과 필터가 생성됩니다.이러한 토폴로지는 네트워크 토폴로지가 동일하더라도 하이패스 및 로우패스 토폴로지로 설명될 수 있습니다.이러한 개체 클래스(즉, 구성 요소 유형이 지정되지만 절대 값이 지정되지 않은 네트워크)를 보다 정확하게 나타내는 용어는 프로토타입 네트워크입니다.

전자 네트워크 토폴로지는 수학적 토폴로지와 관련이 있으며, 특히 2단자 장치만 포함하는 네트워크의 경우 회로 토폴로지는 그래프 이론의 적용으로 볼 수 있습니다.위상학적 관점에서 이러한 회로의 네트워크 분석에서 네트워크 노드는 그래프 이론의 정점이고 네트워크 분기는 그래프 이론의 가장자리입니다.

표준 그래프 이론은 활성 구성 요소 및 집적 회로와 같은 다중 단자 장치를 다루기 위해 확장될 수 있습니다.그래프는 무한 네트워크 분석에도 사용될 수 있습니다.

회로 다이어그램

이 문서의 회로 다이어그램은 전자 ^[1]공학의 일반적인 관례를 따릅니다. 선은 도체를 나타내고, 채워진 작은 원은 도체의 접합을 나타내며, 열린 작은 원은 외부 세계와의 연결을 위한 단자를 나타냅니다.대부분의 경우 임피던스는 직사각형으로 표시됩니다.실제 회로 다이어그램은 저항기, 인덕터, 커패시터 등에 대한 특정 기호를 사용하지만 토폴로지는 네트워크의 구성 요소 유형과 관련이 없으므로 일반 임피던스에 대한 기호가 대신 사용되었습니다.

이 기사의 그래프 이론 섹션은 네트워크를 표현하는 다른 방법을 제공합니다.

토폴로지 이름

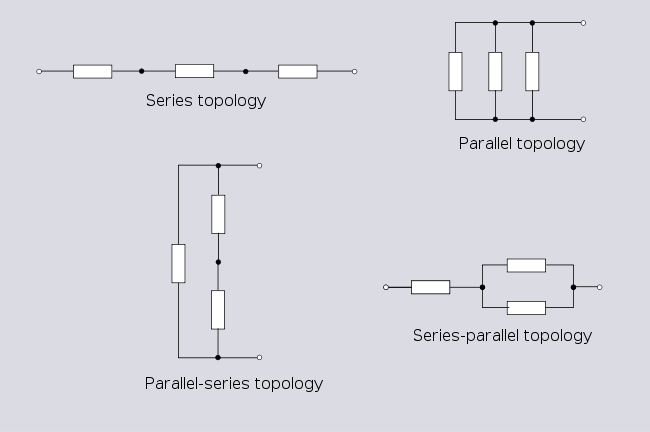
많은 토폴로지 이름은 다이어그램으로 그릴 때 모양과 관련이 있습니다.대부분의 회로는 다양한 방식으로 그려질 수 있으며 결과적으로 다양한 이름을 가집니다.예를 들어, 그림 1.1에 표시된 세 개의 회로는 모두 다르게 보이지만 ^[2]동일한 토폴로지를 가집니다.

이 예제에서는 유사한 알파벳 문자의 이름을 따서 토폴로지를 명명하는 일반적인 관례도 보여 줍니다.그리스어 알파벳 문자도 이러한 방식으로 사용할 수 있습니다(예: π (pi) 토폴로지 및 δ (delta) 토폴로지).

직렬 및 병렬 토폴로지

분기가 두 개인 네트워크의 경우 사용 가능한 토폴로지는 직렬과 병렬 두 가지뿐입니다.

이러한 간단한 토폴로지의 경우에도 회로가 표시되는 방식에는 다양한 차이가 있습니다.

세 개의 분기가 있는 네트워크의 경우 네 가지 토폴로지가 가능합니다.

병렬 직렬 토폴로지는 나중에 설명하는 델타 토폴로지의 또 다른 표현입니다.

연속 및 병렬 토폴로지는 무한대의 더 많은 분기로 계속 구성될 수 있습니다.n개의 분기에서 얻을 수 있는 고유 위상의 수는 2개입니다^n-1.n개 이하의 분기로 얻을 수 있는 총 고유 위상 수는 2-1입니다ⁿ.^[3]

Y 및 Δ 토폴로지

Y와 Δ는 선형 네트워크 분석에서 가장 단순한 3단자 네트워크이기 때문에 중요한 토폴로지입니다.Y-Ω 변환은 선형 회로에 사용할 수 있습니다.직렬 및 병렬 조합으로 분석할 수 없는 일부 네트워크가 있기 때문에 이 변환은 중요합니다.이러한 네트워크는 3상 모터 또는 변압기 권선의 가장 일반적인 두 가지 토폴로지이기 때문에 3상 전원 회로에서 자주 발생합니다.

그림 1.6의 네트워크는 Δ 네트워크와 병렬로 연결된 Y 네트워크로 구성되어 있습니다.네트워크의 두 노드 사이의 임피던스를 계산하는 것이 바람직하다고 가정합니다.많은 네트워크에서 직렬 또는 병렬 임피던스 조합에 대한 규칙을 연속적으로 적용하여 이 작업을 수행할 수 있습니다.그러나 이 경우에는 직렬 및 병렬 ^[4]규칙 외에 Y-Δ 변환이 필요합니다.Y 위상은 스타 위상이라고도 합니다.그러나 별 위상은 ^[5]3개가 아니라 동일한 노드에 연결된 많은 분기의 일반적인 경우를 의미할 수도 있습니다.

단순 필터 토폴로지

그림 1.7에 표시된 토폴로지는 필터 및 감쇠기 설계에 일반적으로 사용됩니다.L-단면은 잠재적 분할기 위상과 동일한 위상입니다.T-섹션은 Y 토폴로지와 동일한 토폴로지입니다.Δ 섹션은 Δ 토폴로지와 동일한 토폴로지입니다.

이러한 모든 토폴로지는 사다리 토폴로지의 짧은 섹션으로 볼 수 있습니다.긴 섹션은 일반적으로 래더 토폴로지로 설명됩니다.이러한 종류의 회로는 일반적으로 2포트 ^[6]네트워크의 관점에서 분석되고 특성화됩니다.

교량 위상

브리지 토폴로지는 브리지 정류기, 휘트스톤 브리지 및 격자 위상 등화기를 포함하여 선형 및 비선형 애플리케이션 모두에서 많은 용도로 사용되는 중요한 토폴로지입니다.브리지 토폴로지가 회로 다이어그램에서 렌더링되는 방법은 여러 가지가 있습니다.그림 1.8의 첫 번째 렌더링은 브리지 회로의 전통적인 묘사입니다.두 번째 렌더링은 브리지 토폴로지와 직렬 및 병렬 조합에 의해 파생된 토폴로지 사이의 동등성을 명확하게 보여줍니다.세 번째 렌더링은 일반적으로 격자 토폴로지로 알려져 있습니다.이것이 위상학적으로 동등하다는 것은 그리 명백하지 않습니다.오른쪽 상단 노드의 오른쪽으로 이동하는 왼쪽 상단 노드를 시각화하면 실제로 그렇게 된다는 것을 알 수 있습니다.

네트워크 브리지 토폴로지는 각각 대각선 방향으로 반대되는 노드 쌍으로 구성된 입력 및 출력 포트가 있는 2포트 네트워크로 사용되는 경우에만 호출하는 것이 일반적입니다.그림 1.7의 박스 토폴로지는 브리지 토폴로지와 동일한 것으로 볼 수 있지만 필터의 경우 입력 및 출력 포트는 각각 인접 노드 쌍입니다.때때로 그림 1.^[7]9와 같이 브리지의 출력 포트에 있는 하중(또는 null 표시) 구성요소가 브리지 토폴로지에 포함됩니다.

브리지 T 및 트윈 T 토폴로지

브리지 T 토폴로지는 Zobel 네트워크 기사에 설명된 방식으로 브리지 토폴로지에서 파생됩니다.동일한 기사에서 논의된 파생 토폴로지도 많습니다.

입력과 출력이 공통(접지) 단자를 공유하는 것이 바람직한 실용적인 응용 분야를 가진 트윈 T 토폴로지도 있습니다.예를 들어 입력 및 출력 연결이 동축 토폴로지로 이루어졌기 때문일 수 있습니다.입력 단자와 출력 단자를 함께 연결하는 것은 일반 브리지 토폴로지에서는 허용되지 않으며, 이러한 이유로 Twin-T는 브리지가 균형 또는 Null 측정 애플리케이션에 사용되는 경우에 사용됩니다.위상은 트윈T 발진기에서도 사인파 발생기로 사용됩니다.그림 1.11의 하단 부분은 브리지 ^[8]토폴로지와의 연결을 강조하기 위해 다시 그려진 트윈 T 토폴로지를 보여줍니다.

무한 위상

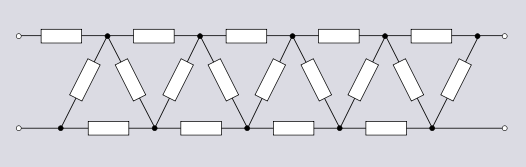
사다리 토폴로지는 제한 없이 확장할 수 있으며 필터 설계에 많이 사용됩니다.래더 토폴로지에는 다양한 변형이 있으며, 그 중 일부는 전자 필터 토폴로지 및 합성 이미지 필터 문서에 설명되어 있습니다.

사다리 위상의 균형 잡힌 형태는 임의의 차수의 프리즘 측면의 그래프로 볼 수 있습니다.반 프리즘의 측면은 이런 의미에서 반 사다리인 위상을 형성합니다.반사다리 위상은 전압 곱셈기 회로, 특히 콕크로프트-월튼 발전기에서 응용 프로그램을 찾습니다.이중 반사다리 ^[9]토폴로지를 사용하는 콕크로프트-월튼 발전기의 전파 버전도 있습니다.

무한 토폴로지는 격자 또는 브리지-T 섹션과 같은 다른 간단한 토폴로지의 여러 섹션을 계단식으로 연결하여 형성할 수도 있습니다.이러한 무한 격자 구간 체인은 전송선의 이론적 분석 및 인공 시뮬레이션에서 발생하지만 실제 회로 ^[10]구현으로 사용되는 경우는 거의 없습니다.

단자가 세 개 이상인 구성 요소

단자가 3개 이상인 구성요소를 포함하는 회로는 가능한 토폴로지의 수를 크게 증가시킵니다.반대로, 토폴로지로 표시되는 서로 다른 회로의 수는 감소하며, 많은 경우 특정 구성 요소가 식별되지 않더라도 토폴로지에서 회로를 쉽게 인식할 수 있습니다.

그림 1.14공통 이미터 쌍극 접합 트랜지스터 앰프와 같은 기본 앰프 토폴로지

그림 1.15긴 꼬리 쌍 증폭기와 같은 균형 증폭기

더 복잡한 회로에서는 구성 ^[11]요소의 토폴로지가 아닌 네트워크 포트 간의 전송 기능을 지정하여 설명을 진행할 수 있습니다.

그래프 이론

그래프 이론은 그래프를 다루는 수학의 한 분야입니다.네트워크 분석에서 그래프는 분석 중인 네트워크를 나타내기 위해 광범위하게 사용됩니다.네트워크의 그래프는 네트워크의 특정 측면, 즉 연결 또는 토폴로지와 관련된 측면만 캡처합니다.많은 네트워크 방정식이 동일한 토폴로지를 가진 네트워크에서 불변하기 때문에 네트워크의 유용한 표현 및 일반화가 될 수 있습니다.여기에는 키르히호프의 법칙과 텔레겐의 [12]정리에서 파생된 방정식이 포함됩니다.

역사

그래프 이론은 키르히호프의 법칙이 공식화된 거의 순간부터 선형 수동 네트워크의 네트워크 분석에 사용되었습니다.1847년에 Gustav Kirchhoff 자신은 저항 ^[13]회로의 루프 분석에서 네트워크의 추상적인 표현으로 그래프를 사용했습니다.이 접근 방식은 나중에 RLC 회로로 일반화되어 저항을 임피던스로 대체했습니다.1873년 제임스 클러크 맥스웰은 노드 ^[14][15]분석과 함께 이 분석의 이중성을 제공했습니다.맥스웰은 또한 노드 어드미턴스 행렬의 결정 요인이 모든 트리 어드미턴스 곱의 합과 같다는 위상 정리를 담당합니다.1900년 앙리 푸앵카레는 그래프를 입사 ^[16]행렬로 표현하는 아이디어를 도입하여 대수 위상학의 분야를 설립했습니다.1916년 오스왈드 베블렌은 푸앵카레의 대수 위상을 키르히호프의 ^[17]분석에 적용했습니다.또한 Veblen은 호환 가능한 네트워크 ^[18]변수 집합을 선택하는 데 도움이 되는 스패닝 트리의 도입을 담당합니다.

전기 회로에 적용되는 네트워크 그래프의 포괄적인 카탈로그화는 1891년 Percy MacMahon(1892년 The Electrician의 엔지니어 친화적인 기사와 함께)에서 시작되었습니다. 그는 조사를 직렬 및 병렬 조합으로 제한했습니다.맥마흔은 이 그래프들을 ^{[note 1]}요크 체인이라고 불렀습니다.로널드 M. 1932년 Foster는 그래프를 무효 또는 순위에 따라 분류하고 소수의 노드를 가진 모든 그래프에 대한 차트를 제공했습니다.이 작업은 1920년 George Campbell과 4포트 전화 중계기에 대한 공동 연구를 진행하면서 Foster가 이전에 실시한 설문 조사에서 발전하여 83,539개의 개별 ^[19]그래프를 생성했습니다.

오랫동안 전기 회로 이론의 토폴로지는 선형 수동 네트워크에만 관심이 있었습니다.반도체 장치 및 회로의 최근 발전으로 인해 토폴로지에 새로운 도구가 필요하게 되었습니다.회로 복잡성의 엄청난 증가는 컴퓨터 ^[18]계산의 효율성을 향상시키기 위해 그래프 이론에서 조합론의 사용으로 이어졌습니다.

그래프 및 회로 다이어그램

네트워크는 일반적으로 네트워크를 구성하는 전기 요소의 종류에 따라 분류됩니다.회로 다이어그램에서 이러한 요소 종류는 각각 고유한 기호를 사용하여 특별히 그려집니다.저항성 네트워크는 R 요소로만 구성된 단일 요소 유형의 네트워크입니다.마찬가지로 정전식 또는 유도식 네트워크는 단일 요소 유형입니다.RC, RL 및 LC 회로는 단순한 2원소 종류의 네트워크입니다.RLC 회로는 가장 단순한 3원소 종류의 네트워크입니다.저역 통과 필터에 일반적으로 사용되는 LC 래더 네트워크는 많은 요소를 가질 수 있지만 2요소 종류 ^[20]네트워크의 또 다른 예입니다.

반대로 토폴로지는 네트워크 요소 간의 기하학적 관계에만 관련되며 요소의 종류 자체에는 관련되지 않습니다.네트워크의 위상학적 표현의 핵심은 네트워크의 그래프입니다.요소는 그래프의 가장자리로 표시됩니다.가장자리는 다른 가장자리(요소)가 나올 수 있는 점 또는 작은 원 위에서 끝나는 선으로 그려집니다.회로 분석에서 그래프의 가장자리를 분기라고 합니다.점은 그래프의 정점이라고 하며 네트워크의 노드를 나타냅니다.노드와 정점은 네트워크 그래프를 논의할 때 서로 바꾸어 사용할 수 있는 용어입니다.그림 2.2는 그림 2.^[21]1의 회로를 그래프로 나타낸 것입니다.

네트워크 분석에 사용되는 그래프는 일반적으로 전류 흐름과 전압의 방향을 캡처하기 위한 방향 그래프와 분기와 노드의 고유성을 캡처하기 위한 레이블이 지정된 그래프 모두입니다.예를 들어, 가지에 고유한 레이블이 지정되지 않은 경우 두 개의 가지가 서로 교환된 경우에도 가지의 제곱으로 구성된 그래프는 동일한 위상 그래프가 됩니다.방향 지정된 그래프에서 분기가 연결되는 두 노드는 소스 및 대상 노드로 지정됩니다.일반적으로 ^[22]분기에 그려진 화살표로 표시됩니다.

입사

입사는 그래프의 기본 속성 중 하나입니다.꼭짓점에 연결된 가장자리는 그 꼭짓점에 입사한다고 합니다.그래프의 입사는 입사 행렬이라는 행렬을 사용하여 행렬 형식으로 캡처할 수 있습니다.사실, 입사 행렬은 그래프의 대안적인 수학적 표현이며, 어떤 종류의 그림도 필요하지 않습니다.행렬 행은 노드에 해당하고 행렬 열은 분기에 해당합니다.행렬의 원소는 입사가 없는 경우 0이거나 노드와 분기 사이의 입사에 대해 1입니다.방향 그래프의 방향은 ^[18][23]요소 기호로 표시됩니다.

등가성

그래프는 하나가 변형에 의해 다른 하나로 변환될 수 있는 경우에 동일합니다.변형에는 변환, 회전 및 반사, 가지 굽힘 및 신장, 가지 교차 또는 매듭 작업이 포함될 수 있습니다.변형을 통해 동등한 두 그래프가 ^[24]일치한다고 합니다.

전기 네트워크 분야에서는 일치 그래프를 생성하지 않는 동등한 그래프를 생성하는 것으로 간주되는 두 가지 추가 변환이 있습니다.이 중 첫 번째는 직렬로 연결된 분기의 교환입니다.이것은 특별한 규칙 없이 변형을 통해 달성할 수 있는 병렬 연결된 분기의 상호 교환의 이중입니다.두 번째는 두 개 이상의 개별 부분으로 분할된 그래프, 즉 각 세트의 노드에 분기가 발생하지 않는 두 세트의 노드가 있는 그래프에 관한 것입니다.이렇게 분리된 두 개의 부품은 각각의 노드를 하나의 노드로 결합하여 부품이 결합되는 하나의 그래프와 동등한 것으로 간주됩니다.마찬가지로 노드를 둘로 분할하여 두 개의 개별 부분으로 분할할 수 있는 그래프도 동등한 ^[25]것으로 간주됩니다.

트리 및 링크

트리는 모든 노드가 분기에 의해 직접 또는 간접적으로 연결되지만 닫힌 루프를 형성하지 않는 그래프입니다.닫힌 루프가 없기 때문에 트리에는 전류가 없습니다.네트워크 분석에서 우리는 스패닝 트리, 즉 네트워크 그래프에 있는 모든 노드를 연결하는 트리에 관심이 있습니다.이 문서에서 스패닝 트리는 달리 명시되지 않은 한 무자격 트리를 의미합니다.주어진 네트워크 그래프에는 여러 개의 서로 다른 트리가 포함될 수 있습니다.트리를 형성하기 위해 그래프에서 제거된 가지를 링크라고 하며, 트리에 남아 있는 가지를 잔가지라고 합니다.노드가 n개인 그래프의 경우 각 트리의 분기 수 t는 다음과 같아야 합니다.

${\displaystyle t=n-1\}$

회로 분석을 위한 중요한 관계는 다음과 같습니다.

$\"디스플레이 스타일 b=\ell +t\"$

여기서 b는 그래프의 분기 수이고 ℓ는 ^[26]트리를 형성하기 위해 제거된 링크 수입니다.

타이 세트 및 컷 세트

회로 분석의 목표는 네트워크의 모든 분기 전류와 전압을 결정하는 것입니다.이러한 네트워크 변수가 모두 독립적인 것은 아닙니다.분기 전압은 구성된 소자의 전송 기능에 의해 분기 전류와 관련됩니다.따라서 네트워크의 완전한 솔루션은 분기 전류 또는 분기 전압 측면에서만 가능합니다.또한 모든 분기 전류가 서로 독립적이지도 않습니다.완전한 솔루션에 필요한 분기 전류의 최소 수는 l입니다.이것은 트리가 링크를 제거했기 때문에 트리에 전류가 있을 수 없습니다.트리의 나머지 분기는 전류가 0이므로 링크 전류와 독립적일 수 없습니다.독립 변수 집합으로 선택된 분기 전류는 트리의 링크와 연결된 집합이어야 합니다. 임의로 ^[27]모든 분기를 선택할 수 없습니다.

분기 전압의 관점에서 t 분기 전압으로 네트워크의 완전한 솔루션을 얻을 수 있습니다.이것은 트리의 모든 분기를 단락시키면 전압이 모든 곳에서 0이 된다는 사실의 결과입니다.따라서 링크 전압은 트리 분기 ^[28]전압과 독립적일 수 없습니다.

일반적인 분석 방법은 분기 전류가 아닌 루프 전류를 해결하는 것입니다.분기 전류는 루프 전류의 관점에서 발견됩니다.루프 전류 세트는 임의로 선택할 수 없습니다.독립 변수 집합을 보장하려면 루프 전류가 특정 루프 집합과 관련된 전류여야 합니다.이 루프 세트는 분석할 회로 그래프의 주어진 트리의 단일 링크를 대체하여 형성된 루프로 구성됩니다.트리에서 단일 링크를 대체하는 것은 정확히 하나의 고유 루프를 형성하기 때문에, 이렇게 정의된 루프 전류의 수는 l과 같습니다.이 맥락에서 루프라는 용어는 그래프 이론에서 루프의 일반적인 의미와 다릅니다.주어진 루프를 형성하는 분기 집합을 타이 ^{[note 2]}집합이라고 합니다.네트워크 방정식 세트는 루프 전류를 타이 세트 분기 ^[29]전류의 대수 합계와 동일하게 하여 형성됩니다.

트리 및 타이 세트를 참조하지 않고 독립 루프 전류 세트를 선택할 수 있습니다.독립적인 루프 세트를 선택하기 위한 충분하지만 필요하지 않은 조건은 선택된 각 루프에 이미 선택된 루프에 의해 포함되지 않은 적어도 하나의 분기가 포함되도록 하는 것입니다.특히 간단한 선택은 모든 루프가 ^{[note 3]}메시로 선택되는 메시 분석에 사용되는 것입니다.메쉬 분석은 분기가 교차하지 않고 그래프를 평면 또는 구체에 매핑할 수 있는 경우에만 적용할 수 있습니다.이러한 그래프를 평면 그래프라고 합니다.평면 또는 구체에 매핑할 수 있는 능력은 동등한 조건입니다.평면에 매핑된 유한 그래프는 구체의 작은 영역에 매핑될 때까지 축소될 수 있습니다.반대로, 구에 매핑된 그래프의 메시는 그 안의 공간이 구의 거의 모든 부분을 차지할 때까지 늘어날 수 있습니다.그러면 전체 그래프가 구의 작은 영역만 차지합니다.이는 첫 번째 경우와 동일하므로 그래프도 ^[30]평면에 매핑됩니다.

루프 전류 방법과 유사하고 이중적인 전압을 가진 네트워크 변수를 선택하는 방법이 있습니다.여기서 노드 쌍과 관련된 전압은 기본 변수이며 분기 전압은 이 변수의 관점에서 확인됩니다.또한 이 방법에서는 모든 변수가 독립적인지 확인하기 위해 그래프의 특정 트리를 선택해야 합니다.타이 세트의 듀얼은 컷 세트입니다.하나를 제외한 모든 그래프 링크를 개방 회로로 허용하여 타이 세트가 형성됩니다.절단 세트는 트리 가지 중 하나를 제외한 모든 가지가 단락되도록 하여 형성됩니다.절단 세트는 단락되지 않은 트리 분기와 다른 트리 분기에 의해 단락되지 않은 링크로 구성됩니다.그래프의 잘라내기 집합은 두 개의 분리된 하위 그래프를 생성합니다. 즉, 그래프를 두 부분으로 잘라내는 데 필요한 최소한의 분기 집합입니다.네트워크 방정식 세트는 노드 쌍 전압을 절단 세트 분기 ^[31]전압의 대수 합계와 동일하게 하여 형성됩니다.망사 분석의 특수한 경우의 이중성은 결절 ^[32]분석입니다.

무효 및 순위

s개의 부분과 b개의 분기를 갖는 그래프의 무효값 N은 다음과 같이 정의됩니다:

${\displaystyle N=b-n+s\} 표시$

그래프의 null은 네트워크 방정식 집합의 자유도를 나타냅니다.평면 그래프의 경우 귀무 가설은 ^[33]그래프의 메시 수와 같습니다.

그래프의 순위 R은 다음과 같이 정의됩니다.

${\displaystyle R=n-s\} 표시$

순위는 결절 분석에서 망사 분석에서 귀무가 수행하는 것과 동일한 역할을 합니다.즉, 필요한 노드 전압 방정식의 수를 제공합니다.순위와 무효는 이중 개념이며 다음과 ^[34]관련이 있습니다.

${\displaystyle R+N=b\} 표시$

네트워크 변수 해결

일단 기하학적으로 독립적인 변수들의 집합이 선택되면, 네트워크의 상태는 이것들로 표현됩니다.결과는 네트워크 변수의 값을 찾기 위해 동시에 해결해야 하는 일련의 독립적인 선형 방정식입니다.이 방정식 세트는 네트워크의 특성 매개 변수 행렬로 이어지는 행렬 형식으로 표현될 수 있습니다.매개변수 행렬은 방정식이 루프 분석 기반으로 형성된 경우 임피던스 행렬의 형태를 취하거나, 방정식이 노드 분석 ^[35]기반으로 형성된 경우 어드미턴스 행렬의 형태를 취합니다.

이 방정식들은 잘 알려진 많은 방법으로 풀 수 있습니다.한 가지 방법은 ^[36]변수를 체계적으로 제거하는 것입니다.또 다른 방법은 결정 요인의 사용을 포함합니다.이것은 Cramer의 규칙으로 알려져 있으며 결정 요인의 관점에서 알 수 없는 변수에 대한 직접적인 표현을 제공합니다.이는 솔루션에 대한 간결한 표현식을 제공한다는 점에서 유용합니다.그러나 가장 사소한 네트워크 이상의 경우 ^[37]수동으로 작업할 때 이 방법에 대해 더 많은 계산 노력이 필요합니다.

이중성

하나의 분기와 노드 쌍 사이의 관계가 다른 하나의 분기와 루프 사이의 관계와 같으면 두 그래프는 이중 그래프입니다.그래프의 이중성은 전적으로 그래픽 ^[38]방법으로 찾을 수 있습니다.

그래프의 이원은 또 다른 그래프입니다.그래프에서 주어진 트리의 경우, 보완적인 가지 집합(즉, 트리에 없는 가지)이 이중 그래프에서 트리를 형성합니다.원래 그래프와 트리의 타이 세트와 관련된 전류 루프 방정식 세트는 이중 ^[39]그래프의 절단 세트와 관련된 전압 노드 쌍 방정식 세트와 동일합니다.

다음 표에는 회로 ^[40]이론과 관련된 토폴로지의 이중 개념이 나와 있습니다.

이중 개념 요약

현재의	전압
나무	메이즈
분점	분점
메쉬	노드
고리	노드 쌍
링크	나뭇가지
타이 세트	컷 세트
단락	단선
병렬 연결	직렬 연결
무효	순위

나무의 이중성은 때때로 미로라고^{[note 4]} 불립니다. 그것은 ^[41]나무가 나뭇가지로 연결된 노드로 구성된 것과 같은 방식으로 링크로 연결된 공간으로 구성됩니다.

모든 그래프에 대해 이원을 만들 수는 없습니다.이중성을 사용하려면 모든 타이 세트에 이중 그래프에 이중 절단 세트가 있어야 합니다.이 조건은 그래프가 분기가 교차하지 않는 구에 매핑할 수 있는 경우에만 충족됩니다.이를 확인하려면 그래프를 두 부분으로 "연결"하기 위해 타이 세트가 필요하고 그래프를 두 부분으로 자르기 위해 이중 컷 세트가 필요합니다.구체에 매핑되지 않는 유한 네트워크의 그래프에는 n-fold 토러스가 필요합니다.토러스의 구멍을 통과하는 동점 집합은 그래프를 두 부분으로 묶지 못합니다.따라서 이중 그래프는 두 부분으로 잘리지 않으며 필요한 절단 세트를 포함하지 않습니다.결과적으로 평면 그래프에만 ^[42]이중이 있습니다.

또한 대응하는 용량성 요소가 없기 때문에 상호 인덕턴스를 포함하는 네트워크에 대해 듀얼을 구성할 수 없습니다.듀얼이 있는 동등한 회로를 개발할 수 있지만, 듀얼은 상호 인덕턴스로 ^[43]직접 구성할 수 없습니다.

노드 및 메시 제거

일련의 네트워크 방정식에 대한 작업은 발생하는 상황을 시각화하는 데 도움이 될 수 있는 위상학적 의미를 가집니다.일련의 네트워크 방정식에서 노드 전압을 제거하는 것은 위상적으로 그래프에서 해당 노드를 제거하는 것과 일치합니다.세 개의 다른 노드에 연결된 노드의 경우, 이는 잘 알려진 Y-Δ 변환에 해당합니다.변환은 더 많은 연결된 노드로 확장될 수 있으며 스타 메시 ^[44]변환이라고 합니다.

이 변환의 역변환은 분석적으로 메시 전류의 제거에 해당하고 위상적으로 메시의 제거에 해당하는 Δ-Y 변환입니다.그러나 임의의 수의 다른 메시와 공통적으로 가지가 있는 메시 전류를 제거하면 일반적으로 실현 가능한 그래프가 생성되지 않습니다.이는 일반적인 별의 변환 그래프가 구에 매핑되지 않는 그래프이기 때문입니다(별 다각형을 포함하므로 다중 교차).이러한 그래프의 이원은 존재할 수 없지만 일반화된 메시 제거를 ^[44]나타내는 데 필요한 그래프입니다.

상호 결합

종래의 회로 그래프 표현에서는 변압기에서 발생하는 것과 같이 상호 유도 결합을 명시적으로 표현하는 수단이 없으며, 이러한 구성 요소는 둘 이상의 별도 부분을 갖는 단절된 그래프를 초래할 수 있습니다.분석의 편의를 위해 여러 부품이 있는 그래프를 각 부품의 노드 하나를 단일 노드로 통합하여 하나의 그래프로 결합할 수 있습니다.이는 회로의 이론적 거동에 영향을 미치지 않으므로 회로에 대한 분석은 여전히 유효합니다.그러나 회로가 이러한 방식으로 구현되면 부품 간의 절연이 파괴된다는 점에서 실질적인 차이가 발생할 수 있습니다.예를 들어 1차 측과 2차 측 모두에서 접지된 변압기를 들 수 있습니다.변압기는 여전히 동일한 전압비의 변압기 역할을 하지만 이제는 더 이상 절연 ^[45]변압기로 사용할 수 없습니다.

그래프 이론의 보다 최근 기술은 기존 이론에서도 문제가 되는 활성 성분을 다룰 수 있습니다.이러한 새로운 기술은 또한 상호 ^[46]결합을 다룰 수 있습니다.

활성 구성 요소

상호 커플링 및 활성 구성 요소를 처리하는 데 사용할 수 있는 두 가지 기본 접근 방식이 있습니다.1953년에 Samuel Jefferson Mason은 신호 흐름 ^[47]그래프를 도입했습니다.신호 흐름 그래프는 가중치가 부여된 방향 그래프입니다.그는 상호 커플링과 활성 네트워크를 포함하는 회로를 분석하기 위해 이것들을 사용했습니다.이러한 그래프에서 방향 에지의 가중치는 증폭기가 갖는 것과 같은 이득을 나타냅니다.일반적으로 신호 흐름 그래프는 위에서 설명한 일반적인 방향 그래프와 달리 구성 ^[46]요소의 물리적 배열 토폴로지에 해당하지 않습니다.

두 번째 접근법은 상호 커플링 및 활성 구성요소를 포함하도록 기존 방법을 확장하는 것입니다.이를 달성하기 위한 몇 가지 방법이 제안되었습니다.이 중 하나는 회로의 전류를 나타내는 그래프이고 다른 하나는 전압을 나타내는 그래프인 두 개의 그래프가 구성됩니다.패시브 구성 요소는 두 트리 모두에서 동일한 분기를 가지지만 활성 구성 요소는 그렇지 않을 수 있습니다.이 방법은 두 그래프에 공통적인 스패닝 트리를 식별하는 데 의존합니다.1965년 ^{[note 5]}Chen에 의해 하나의 그래프만 필요로 하는 고전적 접근법을 확장하는 대안이 제안되었습니다.Chen의 방법은 뿌리 깊은 ^[46]나무를 기반으로 합니다.

하이퍼그래프

활성 성분에 대한 고전적인 그래프 이론을 확장하는 또 다른 방법은 하이퍼그래프를 사용하는 것입니다.일부 전자 부품은 그래프를 사용하여 자연스럽게 표시되지 않습니다.트랜지스터에는 세 개의 연결 지점이 있지만 일반 그래프 분기는 두 개의 노드에만 연결할 수 있습니다.현대의 집적 회로는 이보다 더 많은 연결을 가지고 있습니다.이 문제는 일반 ^[48]그래프 대신 하이퍼 그래프를 사용하여 해결할 수 있습니다.

일반적인 표현에서는 각 구성 요소가 두 개의 노드에 연결되는 에지로 표시됩니다.하이퍼그래프에서 구성 요소는 임의의 수의 노드에 연결할 수 있는 하이퍼 에지로 표시됩니다.하이퍼 에지에는 하이퍼 에지를 노드에 연결하는 촉수가 있습니다.하이퍼 에지의 그래픽 표현은 상자일 수 있으며(선인 에지와 비교하여) 촉수의 표현은 상자에서 연결된 노드까지의 선입니다.유향 하이퍼그래프에서 촉수는 하이퍼 에지의 레이블에 의해 결정되는 레이블을 운반합니다.전통적인 방향 그래프는 각각 두 개의 촉수를 가진 하이퍼그래프로 생각할 수 있습니다.이 두 촉수는 출처와 대상으로 표시되며 일반적으로 화살표로 표시됩니다.촉수가 더 많은 일반 하이퍼그래프에서는 더 복잡한 레이블링이 ^[49]필요합니다.

하이퍼그래프는 입사 행렬에 의해 특징지어질 수 있습니다.두 개의 종단 성분만 포함하는 정규 그래프에는 각 행에 0이 아닌 항목이 정확히 두 개 있습니다.모든 행에 0이 아닌 항목이 두 개 이상 있는 발생 행렬은 하이퍼그래프를 나타냅니다.행에 있는 0이 아닌 항목의 수는 해당 분기의 순위이고, 가장 높은 분기 순위는 ^[50]발생 행렬의 순위입니다.

비균질 변수

고전적인 네트워크 분석은 네트워크 변수가 전류(루프 분석) 또는 전압(노드 분석)에서 균일한 네트워크 방정식 세트를 개발합니다.이렇게 발견된 네트워크 변수 집합은 독립 방정식 집합을 구성하는 데 필요한 최소 값이 아닙니다.노드 분석에 대한 루프 분석의 변수 수에는 차이가 있을 수 있습니다.경우에 따라 균질성에 대한 요구 사항이 완화되고 전류 및 전압 변수의 혼합이 허용되는 경우 가능한 최소 수가 이들 중 어느 것보다 작을 수 있습니다.1967년^{[note 6]} Kishi와 Katajini의 결과는 네트워크의 동작을 설명하는 데 필요한 절대 최소 변수 수가 네트워크 ^[46]그래프의 두 가지^{[note 8]} 확장 포레스트 사이의 최대^{[note 7]} 거리로 제공된다는 것입니다.

네트워크 합성

그래프 이론은 네트워크 합성에 적용될 수 있습니다.고전적인 네트워크 합성은 많은 표준 형식 중 하나로 필요한 네트워크를 실현합니다.표준 형식의 예는 코우어의 표준 사다리 네트워크 또는 포스터의 표준 형식에 의한 구동점 임피던스의 실현 또는 브룬의 양의 실제 함수로부터의 유입의 실현입니다.그러나 위상학적 방법은 주어진 표준 형식에서 시작되지 않습니다.오히려, 그 형태는 수학적 표현의 결과입니다.일부 표준 형식은 실현을 위해 상호 인덕턴스를 필요로 합니다.네트워크 합성의 위상학적 방법의 주요 목표는 이러한 상호 인덕턴스의 필요성을 제거하는 것이었습니다.위상에서 나오는 한 가지 정리는 상호 결합이 없는 구동점 임피던스의 실현은 모든 인덕터 또는 모든 커패시터 ^[51]루프가 없는 경우에만 최소화된다는 것입니다.

그래프 이론은 네트워크의 요소가 실수(저항 네트워크와 같은 단일 요소 종류 네트워크) 또는 이진 상태(스위칭 ^[46]네트워크와 같은)로 표현될 수 있을 때 네트워크 합성에서 가장 강력합니다.

무한 네트워크

아마도, 연구된 무한 그래프를 가진 가장 초기의 네트워크는 1881년 올리버 헤비사이드에 의해 개발된 전송선을 마지막 형태로 나타내기 위해 사용된 사다리 네트워크였을 것입니다.확실히 무한 네트워크에 대한 모든 초기 연구는 동일한 요소가 반복되는 사다리 또는 그리드와 같은 주기적인 구조로 제한되었습니다.20세기 후반이 되어서야 임의 토폴로지를 사용하여 무한 네트워크를 분석하는 도구를 사용할 ^[52]수 있게 되었습니다.

무한 네트워크는 대체로 이론적인 관심사일 뿐이며 수학자들의 놀이입니다.실제 제한에 의해 제약을 받지 않는 무한 네트워크는 몇 가지 매우 비물리적인 특성을 가질 수 있습니다.예를 들어, 키르히호프의 법칙은 경우에 따라 실패할 수 있으며 무한대에서의 종단에 의존하는 구동점 임피던스를 갖는 무한 저항 사다리를 정의할 수 있습니다.이론적 무한 네트워크의 또 다른 비물리적 특성은 일반적으로 옴의 법칙과 키르히호프의 법칙과 같은 일반적인 네트워크 법칙 외에 제약이 가해지지 않는 한 무한 전력을 소멸시킨다는 것입니다.그러나 일부 실제 응용 프로그램이 있습니다.전송선 예제는 무한소 요소(분산 요소 모델)로 모델링할 수 있는 실제 문제 클래스 중 하나입니다.다른 예로는 연속 매체에 파동을 발사하는 것, 프린징 필드 문제, 기판의 점 사이 또는 보어홀 ^[53]아래의 저항 측정 등이 있습니다.

초무한 네트워크는 무한 네트워크의 개념을 더욱 확장합니다.무한 네트워크의 가장자리에 있는 노드는 다른 분기를 연결하여 다른 네트워크로 연결할 수 있습니다.이 새로운 네트워크는 그 자체로 무한할 수 있습니다.따라서, 토폴로지는 그들 사이에 유한한 경로가 없는 노드 쌍을 갖는 구성될 수 있습니다.이러한 무한 네트워크의 네트워크를 초무한 ^[54]네트워크라고 합니다.

메모들

참고 항목

• 기호 회로 분석
• 네트워크 토폴로지

레퍼런스

서지학

• 브리튼, 제임스 E., 로딩 코일의 도입:조지 A.캠벨과 마이클 1세"푸핀", 기술과 문화, 11권, 1호, 36-57페이지, 존스 홉킨스 대학 출판부, 1970년 1월도이:10.2307/3102809.
• 캠벨, G. A., "전파 필터의 물리 이론", 벨 시스템 기술 저널, 1922년 11월, vol. 1, no. 2, pp. 1-32.
• Cederbaum, I., "네트워크 분석 및 합성에 대한 그래프 이론의 일부 적용", IEEE 회로 및 시스템 거래, vol.31, iss.1, 페이지 64–68, 1984년 1월.
• Farago, P. S., 선형 네트워크 분석 입문, The English University Press Ltd, 1961.
• Foster, Ronald M., "전기 네트워크의 기하학적 회로", American Institute of Electric Engineers, vol.51, iss.2, 309–317, 1932년 6월.
• Foster, Ronald M.; Campbell, George A., "전화 변전소와 중계기 회로를 위한 최대 출력 네트워크", American Institute of Electric Engineers, vol.39, iss.1, pp. 230–290, 1920년 1월.
• 길르민, 에른스트 A., 소개 회로 이론, 뉴욕: 존 와일리 & 선즈, 1953 OCLC 535111
• 친절, 디터; 페서, 커트, 고전압 테스트 기술, 번역기 Y.Narayana Rao, Newnes, 2001 ISBN 0-7506-5183-0.
• Genya의 Kishi, Kajitani, Yoji, "선형 그래프의 최대 거리 나무와 주요 분할", IEEE 회로 이론 거래, vol.16, iss.3, 페이지 323–330, 1969년 8월.
• MacMahon, Percy A., "나무"라고 불리는 분석 형태와 관련된 요크 체인 및 다당제 구성, 런던 수학회 의사록, vol.22 (1891), pp.330–346 doi:10.1112/plms/s1-22.1.330.
• MacMahon, Percy A., "저항의 조합", The Electrician, vol.28, 601–602, 1892년 4월 8일.
  이산 응용 수학, vol.54, iss.에 재인쇄됨.2-3호, 225-228페이지, 1994년 10월 17일 도이: 10.1016/0166-218X(94)90024-8.
• Minas, M., "도표의 의미론적 표현 생성", 산업 관련성을 통한 그래프 변환의 적용: 국제 워크샵, AGTIVE'99, Kerkrade, 1999년 9월 1일부터 3일까지: 절차, 페이지 209-224, Springer, 2000 ISBN 3-540-67658-9.
• Redifon Radio Diary, 1970, William Collins Sons & Co, 1969.
• Skiena, Steven S., The Algorithm Design Manual, Springer, 2008, ISBN 1-84800-069-3.
• Suresh, Kumar K. S., "네트워크 토폴로지 소개" 11장, Pearson Education India, 2010 ISBN 81-317-5511-8.
• Tooly, Mike, BTEC First Engineering: BTEC First in Engineering, Routlege, 2010 ISBN 1-85617-685-1에 대한 필수 및 선택 옵션 유닛.
• Wildes, Karl L.; Lindgren, Nilo A., "네트워크 분석 및 합성:에른스트 A."Guillemin", MIT 전기 공학 및 컴퓨터 과학의 세기, 1882–1982, 페이지 154–159, MIT Press, 1985 ISBN 0-262-23119-0.
• 제마니안, Armen H., 무한 전기 네트워크, 캠브리지 대학 출판부, 1991 ISBN 0-521-40153-4.