이차방정식

대수학에서 2차 방정식(, )은 다음과^[1] 같이 표준 형태로 재배열될 수 있는 모든 방정식입니다.

여기서 x는 알 수 없는 값을 나타내고 a, b, c는 알려진 수를 나타냅니다. 여기서 ≠ 0. (a = 0이고 b가 0인 경우 방정식은 2차가 아닌 선형입니다.)숫자 a, b, c는 방정식의 계수이며 각각 2차 계수, 선형 계수 및 상수 계수 또는 자유항을 불러 구별할 수 있습니다.^[2]

식을 만족하는 x의 값을 식의 해라고 하고, 식의 좌변에 있는 근 또는 0이라고 합니다.2차 방정식은 많아야 2개의 해를 갖습니다.해법이 하나뿐이라면 이중근이라고 말합니다.모든 계수가 실수인 경우, 두 개의 실수해가 존재하거나, 하나의 실수 이중근이 존재하거나, 또는 서로 복잡한 결합체인 두 개의 복잡한 해가 존재합니다.2차 방정식은 복소수 근이 포함되어 있는 경우 항상 2개의 근을 가지며, 2개의 근에 대해 이중 근이 계산됩니다.2차 방정식을 동등한 방정식으로^[3] 인수분해할 수 있습니다.

여기서 r과 s는 x에 대한 해입니다.

2차 공식

는 해를 a, b, c로 표현합니다.제곱을 완성하는 것은 공식을 도출하는 여러 가지 방법 중 하나입니다.

2차 방정식으로 표현할 수 있는 문제에 대한 해결책은 일찍이 기원전 2000년에 알려져 있었습니다.^[4][5]

2차 방정식은 알려지지 않은 하나만 포함하기 때문에 "일변량"이라고 불립니다.2차 방정식은 음이 아닌 정수인 x의 거듭제곱만 포함하므로 다항식입니다.특히 최대 거듭제곱이 2이므로 2차 다항식입니다.

이차방정식 풀기

실수 계수 또는 복소수 계수를 갖는 2차 방정식은 근이라고 하는 두 개의 해를 가집니다.이 두 가지 솔루션은 서로 다를 수도 있고 그렇지 않을 수도 있으며 실제 솔루션일 수도 있고 그렇지 않을 수도 있습니다.

검사별팩토링

2차 방정식 ax + bx + c = 0을 곱 (px + q) (rx + s) = 0으로 표현하는 것이 가능할 수 있습니다. 어떤 경우에는 간단한 검사를 통해 두 형태를 서로 동등하게 만드는 p, q, r, s의 값을 결정할 수 있습니다.만약 2차 방정식을 두 번째 형태로 쓴다면, "영률 성질"은 px + q = 0 또는 rx + s = 0이면 2차 방정식이 만족된다고 말합니다. 이 두 개의 일차 방정식을 푸는 것은 2차 방정식의 근을 제공합니다.

대부분의 학생들에게 검사에 의한 인수분해는 그들이 노출되는 2차 방정식을 푸는 첫 번째 방법입니다.^{[6]: 202–207} 만약 x + bx + c = 0의 형태로 2차 방정식이 주어지면, 찾는 인수분해는 (x + q)(x + s)의 형태를 가지며, 곱이 c인 b에 더해지는 두 개의 숫자 q와 s를 찾아야 합니다(이는 때때로 "비에타의 규칙"이라고 불리며 비에타의 공식과 관련이 있습니다).예를 들어, (x² + 3)(x + 2)와 같이 x + 5x + 6개의 요인이 있습니다.a가 1과 같지 않은 일반적인 경우는 검사를 통해 요인화할 수 있다고 가정할 때 시행착오 추측과 점검에 상당한 노력이 필요할 수 있습니다.

b = 0 또는 c = 0과 같은 특수한 경우를 제외하고 검사에 의한 인수분해는 유리근을 갖는 2차 방정식에만 적용됩니다.이는 실제 적용에서 발생하는 대부분의 이차 방정식을 검사에 의한 인수분해로 풀 수 없음을 의미합니다.^{[6]: 207}

사각형 완성하기

제곱을 완성하는 과정은 대수적 항등식을 이용합니다.

${\displaystyle x^{2}+2hx+h^{2}=(x+h)^{2}}$

이것은 임의의 2차 방정식을 푸는 데 사용될 수 있는 잘 정의된 알고리즘을 나타냅니다.^{[6]: 207} 표준 형태의 2차 방정식으로 시작하여 ax + bx + c = 0

1. 각 변을 제곱항의 계수인 a로 나눕니다.
2. 양쪽에서 상수항 c/a를 뺀다.
3. 양쪽에 b/a의 1/2 제곱, 즉 x의 계수를 더합니다.이렇게 하면 왼쪽을 완벽한 정사각형으로 변환하여 "정사각형을 완성합니다.
4. 왼쪽 면을 정사각형으로 쓰고 필요한 경우 오른쪽 면을 단순화합니다.
5. 좌변의 제곱근과 우변의 양과 음의 제곱근을 동일시하여 두 개의 선형 방정식을 만듭니다.
6. 두 개의 선형 방정식을 각각 푸세요.

우리는 2x + 4x - 4 = 0을 풀어서 이 알고리즘의 사용을 설명합니다.

${\displaystyle 2x^{2}+4x-4=0}$

${\displaystyle \x^{2}+2x-2=0}$

${\displaystyle \x^{2}+2x=2}$

${\displaystyle \x^{2}+2x+1=2+1}$

${\displaystyle \left(x+1\right)^{2}=3}$

${\displaystyle \x+1=\pm {\sqrt {3}}$

${\displaystyle \x=-1\pm {\sqrt {3}}$

더하기-minus 기호 "±"는 x = -1 + √3과 x = -1 - √3이 모두 2차 방정식의 해임을 나타냅니다.

이차 공식 및 그 유도

제곱을 완성하는 것은 2차 방정식을 풀기 위한 일반적인 공식을 유도하는 데 사용될 수 있습니다.^[9]이제 수학적 증명을 간단히 정리하겠습니다.^[10]다항식 확장을 통해 다음 방정식이 2차 방정식과 같다는 것을 쉽게 알 수 있습니다.

${\displaystyle \left(x+{\frac {b}{2a}}\right)^{2}={\frac {b^{2}-4ac}{4a^{2}}}}$

양변의 제곱근을 구하고 x를 고립시키면 다음을 얻을 수 있습니다.

${\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}}$

일부 출처, 특히 오래된 출처는 ax + 2bx + c = 0 또는 ax - 2bx + c = 0과 같은 2차 방정식의 대체 매개 변수화를 사용합니다. 여기서 b는 일반적인 것의 1/2 크기를 가지며 부호는 반대일 수 있습니다.결과적으로 솔루션의 형태는 약간 다르지만, 그렇지 않은 경우에는 동등합니다.

문헌에서 여러 가지 대안적 파생을 찾을 수 있습니다.이러한 증명은 표준적으로 제곱법을 완성하는 것보다 간단하며, 대수학에서 자주 사용되는 다른 기술의 흥미로운 응용을 나타내거나 수학의 다른 분야에 대한 통찰력을 제공합니다.

덜 알려진 2차 공식은 멀러의 방법에 사용되며, 방정식을 통해 동일한 근을 제공합니다.

${\displaystyle x={\frac {2c}{-b\pm {\sqrt {b^{2}-4ac}}}}}$

이는 근의 곱이 c/a임을 주장하는 비에타의 공식에 의해 표준 2차 공식에서 추론될 수 있습니다.$또한$ ${\displaystyle {2차}^{}}$ 방정식을 x ${\displaystyle {}^{}}$ ${\displaystyle x^{2}$로 나눈 다음 c x -${\displaystyle 2^{}}$+ b ${\displaystyle x}$ -${\displaystyle {}^{}}$+ ${\displaystyle a}$ = ${\displaystyle 0,}$ ${\$$displaystyle$ cx$^{-$2} + bx^{-1} + $a$ = 0,} x - 1에 대해 이를 해결하고 {\displaystyle x^{-1}}을(를) 반전시킵니다.

이 형식의 한 가지 특성은 a = 0일 때 유효한 근 하나를 산출하는 반면, 다른 근은 0으로 나눗셈을 포함한다는 것입니다. a = 0일 때 2차 방정식은 1개의 근을 갖는 선형 방정식이 되기 때문입니다.이와 대조적으로, 이 경우 더 일반적인 공식은 하나의 근에 대해 0으로 나눗셈을 하고 다른 근에 대해 0/0의 불확정 형태를 갖습니다.반면 c = 0일 때 더 일반적인 공식은 두 개의 정확한 근을 산출하는 반면 이 형식은 영 근과 불확정 형태인 0/0을 산출합니다.

a와 c가 모두 0이 아닐 때, 표준 이차 공식과 뮬러의 방법 사이의 동일성,

${\displaystyle {\frac {2c}{-b-{\sqrt {b^{2}-4ac}}}={\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}\,}$

교차 곱셈으로 확인할 수 있으며, 다른 선택 기호에 대해서도 마찬가지입니다.

감소된 이차방정식

선행 계수가 1이 되도록 2차 방정식을 줄이는 것이 편리할 때도 있습니다.이것은 a가 0이 아니기 때문에 항상 가능한 a로 양쪽을 나누어 수행됩니다.이렇게 하면 감소된 2차 방정식이 생성됩니다.^[12]

${\displaystyle x^{2}+px+q=0,}$

여기서 p = b/a, q = c/a.이 단다항식은 원래와 같은 해를 갖습니다.

감소된 2차 방정식의 해에 대한 2차 공식은 다음과 같습니다.

${\displaystyle x={\frac {1}{2}}\left (-p\pm {\sqrt {p^{2}-4q}}\right)}$

아니면, 그와 동등하게

${\displaystyle x=-{\frac {p}{2}}\pm {\sqrt {\left ({\frac {p}{2}}\right)^{2}-q}\,}$

판별자

2차 공식에서 제곱근 부호 아래의 표현은 2차 방정식의 판별자라고 불리며, 종종 대문자 D 또는 대문자 그리스 델타를 사용하여 표현됩니다.^[13]

${\displaystyle \Delta = b^{2}-4ac.}$

실수 계수가 있는 2차 방정식은 1개 또는 2개의 다른 실수 근을 가질 수도 있고, 2개의 다른 복잡한 근을 가질 수도 있습니다.이 경우 판별자는 근의 개수와 성질을 결정합니다.세 가지 경우가 있습니다.

• 만일 판별자가 양성이면, 두 개의 다른 근이 존재합니다.

${\displaystyle {\frac {-b+{\sqrt {\Delta}}}{2a}}\quad {\text{and}}\quad {\frac {-b-{\sqrt {\Delta}}}{2a}}}$

둘 다 실수입니다.유리 계수가 있는 2차 방정식의 경우, 판별 변수가 제곱수이면 근이 유리합니다. 다른 경우에는 2차 비합리적일 수 있습니다.

• 판별자가 0이면 ${\displaystyle \frac{\mathrm{b2a}}{}}$${\displaystyle \frac{}{}}$ ${\displaystyle -{\frac {b}{2a}},$즉 반복 또는 이중 루트 또는 두 개의 동일한 루트라고 하는 하나의 실제 루트가 정확히 존재합니다.

• 판별자가 음이면 진짜 근이 없는 것입니다.${\displaystyle 오히려}$, ${\displaystyle \frac{b2}{}}$ a${\displaystyle \frac{}{}}$+ ${\displaystyle i}$ -${\displaystyle }$δ 2${\displaystyle \frac{a}{}}$ ${\displaystyle 및}$ - ${\displaystyle b2\frac{\sqrt{\mathrm{a}}}{}}$ - ${\displaystyle \frac{}{}}$ -$$δ 2 a$$ ${\displaystyle - {\frac$ {$b}{2a$}}+i${\frac {\sqrt${-\$Delta}}{2a}}\quad$ {\text${and}}\quad${\$frac$ {$b}{2a$}}-i${\frac {\sqrt {-\$Delta}}}, {\frac {-2a}}}

서로의 복잡한 결합체입니다.이 식들에서 i는 허수 단위입니다.

따라서 판별자가 0이 아닌 경우에만 근이 구별되고, 판별자가 음수가 아닌 경우에만 근이 실수입니다.

기하학적 해석

함수 f(x) = ax + bx + c는 2차 함수입니다.임의의 2차 함수의 그래프는 포물선이라고 하는 동일한 일반 모양을 갖습니다.포물선의 위치와 크기, 포물선이 어떻게 열리는지는 a, b, c의 값에 따라 달라집니다.그림 1과 같이 a > 0인 경우 포물선은 최소점을 가지며 위쪽으로 열립니다.a가 0일 경우 포물선은 최대 점을 가지며 아래쪽으로 열립니다.포물선의 극단점은 최소점이든 최대점이든 해당 꼭짓점에 해당합니다.꼭짓점의 x좌표는 $x{\displaystyle }$= - ${\displaystyle \frac{b}{}}$2 a {\displaystyle x = {\tfrac {-b}{2a}}에 위치하며, 이 x값을 함수에 대입하면 꼭짓점의 y좌표를 찾을 수 있습니다.y절편은 점 (0, c)에 위치합니다.

2차 방정식 ax + bx + c = 0의 해는 함수 f(x) = ax + bx + c의 근에 해당하는데, 이는 f(x) = 0이 되는 x의 값이기 때문입니다. 그림 2와 같이 a, b, c가 실수이고 f 의 정의역이 실수의 집합이라면,그러면 f 의 근은 그래프가 x 축에 닿는 점의 x coordin률과 정확하게 됩니다.그림 3과 같이 판별자가 양수이면 그래프는 x축을 두 점에서 만지고, 0이면 그래프가 한 점에서 만지며, 음수이면 그래프가 x축을 만지지 않습니다.

이차 인수분해

용어

${\displaystyle x-r}$

는 다항식의 인자입니다.

${\displaystyle ax^{2}+bx+c}$

r이 2차 방정식의 근일 경우에만

${\displaystyle ax^{2}+bx+c=0.}$

다음은 2차 공식으로부터 다음과 같습니다.

${\displaystyle ax^{2}+bx+c=a\left(x-{\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}\right)\left(x-{\frac {-b-{\sqrt {b^{2}-4ac}}{{2a}}\right).}$

2차가 오직 하나의 구별되는 근만을 가지는 특별한 경우 b = 4ac일 때, 2차 다항식은 다음과 같이 인수분해될 수 있습니다.

${\displaystyle ax^{2}+bx+c=a\left(x+{\frac {b}{2a}}\right)^{2}}}$

그래픽 솔루션

이차방정식의 해들

${\displaystyle ax^{2}+bx+c=0}$

2차 함수의 그래프에서 추론할 수 있습니다.

${\displaystyle f(x)=ax^{2}+bx+c,}$

포물선인 셈이죠.

포물선이 x축과 두 점에서 교차하는 경우 두 개의 실제 근이 존재하며, 이는 이 두 점의 x 좌표입니다(x절편이라고도 함).

포물선이 x축과 접하면 그래프와 포물선 사이의 접점의 x 좌표인 이중근이 존재합니다.

포물선이 x축과 교차하지 않으면 두 개의 복잡한 공액 근이 있습니다.이러한 근은 그래프에서 시각화할 수 없지만 실제 부분과 가상 부분은 시각화할 수 있습니다.^[17]

h와 k를 포물선의 꼭짓점의 x좌표와 y좌표(즉, 최대 또는 최소 y좌표를 갖는 점)라고 합니다.2차 함수를 다시 쓸 수 있습니다.

${\displaystyle y=a(x-h)^{2}+k.}$

d를 포물선의 축에 있는 y좌표 2k의 점과 같은 y좌표를 가진 포물선 위의 점 사이의 거리라고 하자(그림 참조; 포물선의 대칭 때문에 같은 거리를 주는 두 점이 있음).그 다음, 실수 부분은 h이고, 허수 부분은 ±d입니다.즉, 뿌리는

${\displaystyle h+id\quad {\text{and}}\quad h-id,}$

또는 그림의 예의 경우.

${\displaystyle 5+3i\quad {\text{and}}\quad 5-3i.}$

중요성 상실 방지

2차 공식이 정확한 해를 제공하지만, 실수가 부동 소수점 숫자(많은 프로그래밍 언어에서 "실수"라고 함)로 근사화되는 수치 분석에서 일반적인 것처럼 계산 중 실수가 근사화되면 결과는 정확하지 않습니다.이런 맥락에서 2차 공식은 완전히 안정적이지 않습니다.

이는 근의 크기 순서가 다르거나, b와²² b - 4ac가 크기에 가까울 때 발생합니다.이 경우 거의 동일한 두 숫자를 빼면 더 작은 근에서 유의성을 잃거나 치명적인 취소가 발생합니다.이를 방지하기 위해 크기가 더 작은 루트 r을${\displaystyle }$(${\displaystyle c}$/${\displaystyle a}$) / ${\displaystyle R}${\$displaystyle ($c$$/$a)$ / $R}$로 계산할 수 있습니다. 여기서 R은 크기가 더 큰 루트입니다.이는 공식을 사용하는 것과 같습니다.

${\displaystyle x={\frac {-2c}{b\pm {\sqrt {b^{2}-4ac}}}}}$

> ${\displaystyle$ b > $0}$인 경우 더하기 기호를 사용하고 b< ${\displaystyle b$< $0.}$인 경우 빼기 기호를 사용합니다.

두 번째 형태의 취소는 판별자의 항 b와² 4ac 사이에 발생할 수 있는데, 이는 두 근이 매우 가까울 때 발생합니다.이로 인해 뿌리에서 정확한 유효 수치의 최대 절반이 손실될 수 있습니다.^[11][18]

예제 및 응용프로그램

황금 비율은 2차 방정식 $x$ ${\displaystyle 2^{}}$ -${\displaystyle {}^{}}$x${\displaystyle }$- ${\displaystyle 1}$ = ${\displaystyle 0}$의 양의 해로 발견됩니다. {\displaystyle x^{2} - x-1 = 0$.}$

원과 다른 원뿔 구간인 타원, 포물선 및 쌍곡선의 방정식은 두 변수의 2차 방정식입니다.

각도의 코사인 또는 사인이 주어지면 절반 크기의 각도의 코사인 또는 사인을 찾는 것은 2차 방정식을 푸는 것을 포함합니다.

다른 식의 제곱근을 포함하는 식의 제곱근을 포함하는 식을 단순화하는 과정은 2차 방정식의 두 해를 찾는 것을 포함합니다.

데카르트의 정리는 네 개의 키싱(상호 접선) 원에 대해 그들의 반지름이 특정한 2차 방정식을 만족한다는 것을 말합니다.

이심삼각형의 내접원의 반지름, 외접원의 반지름, 그리고 그 원들의 중심 사이의 거리 사이의 관계를 제공하는 푸스 정리에 의해 주어진 방정식.두 원의 중심 사이의 반지름에 대한 거리가 해의 하나인 2차 방정식으로 표현될 수 있습니다.관련된 반지름의 관점에서 동일한 방정식의 다른 해는 외접원의 중심과 접선 사각형의 외접원의 중심 사이의 거리를 제공합니다.

2차 방정식을 풀면 3차 함수의 임계점과 4차 함수의 변곡점이 발견됩니다.

역사

바빌로니아의 수학자들은 일찍이 기원전 2000년에 (옛 바빌로니아 점토판에 표시된) 직사각형의 면적과 면에 관련된 문제들을 풀 수 있었습니다.이 알고리즘은 우르 제3왕조까지 거슬러 올라간다는 증거가 있습니다.^[19]현대 표기법에서 문제는 일반적으로 다음과 같은 형태의 한 쌍의 동시 방정식을 푸는 것을 포함합니다.

${\displaystyle x+y=p,\ xy=q,}$

이것은 x와 y가 방정식의 근이라는 문장에 해당합니다.^{[20]: 86}

${\displaystyle z^{2}+q=pz.}$

바빌로니아의 필경사들이 위 직사각형 문제를 x와 y의 관점에서 해결하기 위해 제시한 단계는 다음과 같습니다.

1. p의 절반을 계산합니다.
2. 결과를 제곱합니다.
3. q를 풉니다.
4. 제곱 테이블을 사용하여 (양의) 제곱근을 구합니다.
5. (1) 단계와 (4) 단계의 결과를 합산하여 x를 제공합니다.

현대 표기법에서 이것은 $x$ = (${\displaystyle p}$2 ) + ( ${\displaystyle \frac{\sqrt{p}}{}}$ 2 ) 2 - q {\displaystyle x =\left ({\frac {p}{2}}\right)+{\sqrt {\left ({\frac {p}{2}\right)^{2}-q}}, 이는 더 큰 실수근(있는 경우)에 대한 현대 2차 공식에 해당하는 x = - b + b 2 - 4 a c 2 a {\displaystyle x = {\frac {-b+{\sqrt {b^{2}-4ac}}{2a}}를 a = 1, b = - 로 계산합니다.p, 그리고 c = q.

바빌로니아, 이집트, 그리스, 중국, 인도에서 2차 방정식을 푸는 데 기하학적 방법이 사용되었습니다.이집트 베를린 파피루스는 중왕국(기원전 2050년~기원전 1650년)까지 거슬러 올라가며, 2항 이차방정식의 해답을 담고 있습니다.^[21]기원전 400년경의 바빌로니아 수학자들과 기원전 200년경의 중국 수학자들은 양의 근을 갖는 2차 방정식을 풀기 위해 기하학적 분해 방법을 사용했습니다.^[22][23]2차 방정식에 대한 규칙은 수학에 관한 중국의 논문인 수학 예술에 관한 9장에 주어졌습니다.^[23][24]이러한 초기의 기하학적 방법은 일반적인 공식이 없었던 것으로 보입니다.그리스 수학자 유클리드는 기원전 300년경에 좀 더 추상적인 기하학적 방법을 만들었습니다.피타고라스와 유클리드는 순수한 기하학적 접근으로 2차 방정식의 해를 찾기 위한 일반적인 절차를 만들었습니다.그리스의 수학자 디오판토스는 산술에서 2차 방정식을 풀었지만, 두 근이 모두 양수일 때도 단 하나의 근만 제공했습니다.^[25]

서기 628년, 인도의 수학자인 브라마굽타는 2차 방정식 ax + bx = c의 첫 번째 명시적인 해를 다음과 같이 제시했습니다: "절대수에 [] 제곱의 4배를 곱한 값에 [] 중간 항의 계수의 제곱을 더하면, 동일한 제곱근은 [c]보다 적습니다.중항의 효율성, 제곱의 두 배로 나눈 것이 값입니다." (Brahmasputasiddanta, Colebrook 번역, 1817, 페이지 346)^{[20]: 87} 이는 다음과 같습니다.

${\displaystyle x={\frac {{\sqrt {4ac+b^{2}}-b}{2a}}}$

서기 7세기에 인도에서 쓰여진 바흐샬리 필사본은 2차 방정식뿐만 아니라 2차 불확정 방정식을 풀기 위한 대수 공식을 포함하고 있습니다( ax/c = y형의 origin).브라마굽타에서 영감을 받은 것으로 추정되는 무함마드 이븐 무사 알콰리즈미 (9세기)는 긍정적인 해결책을 위해 작동하는 일련의 공식을 개발했습니다.^{[original research?]}Al-Khwarizmi는 프로세스에서 기하학적 증명을 제공하면서 모든 2차 방정식에 대해 하나 또는 두 개의 수치 답을 받아들이면서 일반 2차 방정식에 대한 완전한 해를 제공하는 데 더 나아갑니다.^[26]그는 또한 제곱을 완성하는 방법을 설명하고 판별자가 양수여야 한다는 것을 인식했는데, 이는 판별자가 음수이면 2차방정식이 해결책이 없다는 것을 증명하기 위해 기하학적 도형을 준 동시대 '압드 알 함 ī드 이븐 투르크(중앙아시아, 9세기)'가 증명했습니다.알콰리즈미 자신이 부정적인 풀이를 받아들이지 않은 반면, 그의 뒤를 이은 후대의 이슬람 수학자들은 부정적인 풀이는 ^{[26]: 191} 물론 비이성적인 수를 풀이로 받아들였습니다.^[28]특히 아부 카밀 슈자 이븐 아슬람(10세기 이집트)은 비합리적인 수(종종 사각근, 입방근 또는 4근 형태)를 2차 방정식의 해 또는 방정식의 계수로 받아들인 최초의 사람이었습니다.^[29]9세기 인도의 수학자 스리다라는 2차 방정식을 푸는 규칙을 썼습니다.^[30]

유대인 수학자 아브라함 바르 히야 하나시(12세기·스페인)가 유럽 최초로 일반 이차방정식의 풀해를 담은 책을 썼습니다.^[31]그의 해결책은 주로 알콰리즈미의 연구에 바탕을 두었습니다.^[26]중국 수학자 양희(1238~1298 AD)^[32]의 저술은 음의 계수가 'x'인 2차 방정식이 등장하는 최초의 것으로 알려져 있습니다.1545년까지 Gerolamo Cardano는 2차 방정식과 관련된 작업들을 정리했습니다.모든 경우를 다루는 2차 공식은 1594년 사이먼 스테빈에 의해 처음 얻어졌습니다.^[33]1637년 르네 데카르트는 오늘날 우리가 알고 있는 형태의 2차 공식을 포함하는 라 게오메트리를 출판했습니다.

고급주제

근 계산의 대안적 방법

비에타의 공식

비에타의 공식(François Viète의 이름에서 따옴)은 다음과 같은 관계입니다.

${\displaystyle x_{1}+x_{2}=-{\frac {b}{a}},\quad x_{1}x_{2}={\frac {c}{a}}}$

2차 다항식의 근과 그 계수 사이에.그들은 기간별로 관계를 비교함으로써 얻어집니다.

${\displaystyle \left(x-x_{1}\right)\left(x-x_{2}\right)=x^{2}-\left(x_{1}+x_{2)}\right)x+x_{1}x_{2}=0}$

등식으로

${\displaystyle x^{2}+{\frac {b}{a}}x+{\frac {c}{a}}=0.}$

첫 번째 비에타의 공식은 2차 함수를 그래프화하는 데 유용합니다.그래프는 정점을 지나는 수직선에 대해 대칭이므로, 정점의 x 좌표는 뿌리(또는 절편)의 평균에 위치합니다.따라서 꼭짓점의 x좌표는

${\displaystyle x_{V}={\frac {x_{1}+x_{2}}}:{2}}=-{\frac {b}{2a}}.$

y좌표는 위의 결과를 주어진 2차 방정식에 대입하여 얻을 수 있습니다.

${\displaystyle y_{V}=-{\frac {b^{2}}{4a}}+c=-{\frac {b^{2}-4ac}{4a}}}$

정점에 대한 이러한 공식은 공식에서 직접 추론할 수도 있습니다(정사각형 완성 참조).

${\displaystyle ax^{2}+bx+c=a\left(\left(x-{\frac {b}{2a}}\right)^{2}-{\frac {b^{2}-4ac}{4a}\right)}}$

수치 계산을 위해, Vieta의 공식은 한 근이 다른 근보다 훨씬 작은 경우 2차 방정식의 근을 찾는 데 유용한 방법을 제공합니다.만약 x < < x >일 경우 x + x ≈ x를 추정할 수 있습니다.

${\displaystyle x_{1}\approx - {\frac {b}{a}}}$

두 번째 비에타 공식은 다음을 제공합니다.

${\displaystyle x_{2}={\frac {c}{ax_{1}}\approx -{\frac {c}{b}}}$

이 공식들은 하나의 큰 근과 하나의 작은 근의 조건 하에서 2차 공식보다 훨씬 평가하기 쉽습니다. 왜냐하면 2차 공식은 작은 근을 두 개의 거의 동일한 수의 차이로 평가하기 때문입니다(큰 b의 경우). 이는 수치 평가에서 반올림 오차를 발생시킵니다.그림은 (i) 2차 공식을 사용한 직접 평가(뿌리가 서로 값이 가까울 때 정확함)와 (ii) 위의 비에타 공식의 근사치를 기반으로 한 평가(뿌리가 넓게 떨어져 있을 때 정확함)의^{[clarification needed]} 차이를 보여줍니다.선형 계수 b가 증가함에 따라 초기에는 2차 공식이 정확하고, 근사 공식은 정확도가 향상되어 b가 증가함에 따라 방법 간의 차이가 줄어듭니다.그러나 어느 시점에서 2차 공식은 반올림 오차로 인해 정확도를 잃기 시작하는 반면 근사적인 방법은 계속 개선됩니다.결과적으로, 방법들 간의 차이는 2차 공식이 점점 악화됨에 따라 증가하기 시작합니다.

이러한 상황은 안정적인 작동을 보장하기 위해 광범위하게 분리된 루트가 필요한 앰프 설계에서 흔히 발생합니다(단계 응답 참조).

삼각해

계산기 이전 시대에는 계산을 단순화하고 속도를 높이기 위해 다양한 인수로 계산한 결과를 보여주는 숫자 목록인 수학 표를 사용했습니다.로그표와 삼각함수는 수학과 과학 교과서에서 흔히 볼 수 있었습니다.천문학, 천체 항법 및 통계학과 같은 응용 분야를 위해 전문화된 표가 발표되었습니다.프로스타파헤레시스(prosthapaeresis)라고 불리는 수치 근사 방법이 존재했는데, 이는 곱셈과 힘과 뿌리를 얻는 것과 같은 시간 소모적인 작업에 대한 지름길을 제공합니다.^[34]천문학자들은 특히 천체역학 계산에 관련된 긴 일련의 계산 속도를 높일 수 있는 방법에 관심을 기울였습니다.

삼각법 치환의 도움으로 2차 방정식을 푸는 방법의 발전을 이해할 수 있는 것은 이러한 맥락 안에서입니다.2차 방정식의 다음과 같은 대체 형태를 생각해 보십시오.

[1] ${\displaystyle ax^{2}+bx\pm c=0,}$

여기서 a와 c가 모두 양수가 될 수 있도록 ± 기호의 기호를 선택합니다.대체함으로써

[2] ${\displaystyle x={\sqrt {c/a}}\tan \theta }$

를 통해 cos(θ) / c를 곱하면 다음을 얻을 수 있습니다.

[3] ${\displaystyle \sin ^{2}\theta +{\frac {b}{\sqrt {ac}}\sin \theta \cos \pm \cos ^{2}\theta = 0.}$

2개의 θ의 기능을 소개하고 재배열하여, 우리는 다음을 얻습니다.

[4] ${\displaystyle \tan 2\theta _{n}=+2{\frac {\sqrt {ac}}{b}},}$

[5] ${\displaystyle \sin 2\theta _{p}=-2{\frac {\sqrt {ac}}{b}},}$

여기서 첨자 n과 p는 각각 식 [1]의 음 또는 양의 부호의 사용에 해당합니다.식 [4] 또는 [5]에서 찾은 θ 또는 θ의 두 값을 [2]에 대입하면 [1]의 필요한 근을 얻을 수 있습니다.sin 2 θ의 절대값이 통일성을 초과하면 식 [5]에 기초한 해에서 복소근이 발생합니다.이 혼합 삼각법과 로그 테이블 룩업 전략을 사용하여 2차 방정식을 푸는 데 필요한 노력의 양은 로그 테이블만 사용하는 노력의 3분의 2였습니다.^[35]복잡한 근을 계산하려면 다른 삼각법 형태를 사용해야 합니다.^[36]

예를 들어, 7자리 로그 및 삼각형 표를 사용할 수 있다고 가정하고, 다음과 같이 6자리 숫자 정확도를 해결하고자 합니다.

${\displaystyle 4.16130x^{2}+9. 15933x-11.4207=0}$

1. 7자리 룩업 테이블에는 100,000개의 항목만 있을 수 있으며, 7자리에 대한 중간 결과를 계산하려면 일반적으로 인접 항목 간의 보간이 필요합니다.
2. ${\displaystyle \log a=0.6192290,\log b=0.9618637,\log c=1.0576927}$
3. ${\displaystyle 2{\sqrt {ac}}/b=2\times 10^{(0.6192290+1.0576927)/2-0.9618637}=1.505314}$
4. ${\displaystyle \theta =(\tan^{-1}1.505314)/2=28.20169^{\circ }{\text{ or }}-61.79831^{\circ }$
5. ${\displaystyle \log \tan \theta =-0.2706462{\text{ or }}0.2706462}$
6. ${\displaystyle \log {\sqrt {c/a}}=(1.0576927-0.6192290)/2=0. 2192318}$
7. ${\displaystyle x_{}}$ ${\displaystyle 1_{}}$ =$0$2192318 - 0.270${\displaystyle 6_{}}$462 = 0.888353 {\displaystyle x${\displaystyle {\_}_{}}${1} = 1${\displaystyle {\mathrm{0^\{}}_{}}$0.2192318-0.2706${\displaystyle 4_{}}$62} = 0.888353} (유의 6${\displaystyle {\mathrm{개\; 수치\; ro}}_{}}$unded)

${\displaystyle x_{2}=-10^{0.2192318+0.2706462}=-3.08943}$

극좌표의 복잡한 근에 대한 솔루션

실수 계수를 갖는 2차 방정식 $a$ ${\displaystyle {}^{}}$ ${\displaystyle 2{}^{}}$+ b ${\displaystyle x}$+ ${\displaystyle c}$ = {\$displaystyle$ ax$^{2$} + bx + c = 0}이 두 개의 복잡한 근을 가지면, 즉 a와 c가 서로 같은 부호를 가져야 하는 경우, 근에 대한 해는 다음과 같이 극형으로 표현될 수 있습니다.

${\displaystyle x_{1},\,x_{2}=r(\cos \theta \pm i\sin \theta),}$

여기서 $r$ = ${\displaystyle$ r = {\$sqrt {c$}{a$}},$ θ = cos - 1 ⁡ ( - b 2 a c ). {\displaystyle \theta =\cos ^{-1}\left ({\tfrac {-b}{2{\sqrt {ac}}}\right).}

기하해

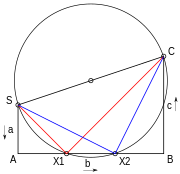
2차 방정식은 기하학적으로 여러 가지 방법으로 풀 수 있습니다.한 가지 방법은 릴의 방법을 통해서 입니다.세 계수 a, b, c는 그림 6의 SA, AB, BC와 같이 직각으로 그립니다.시작점과 끝점 SC를 직경으로 사용하여 원을 그립니다.이것이 세 개의 중간선 AB를 자르면 방정식은 해를 가지며, 해는 A로부터 이 선을 따라 거리를 첫 번째 계수 a 또는 SA로 나눈 음으로 주어집니다.a가 1이면 계수를 직접 판독할 수 있습니다.따라서 다이어그램의 솔루션은 -AX1/SA 및 -AX2/SA입니다.^[38]

토마스 칼라일의 이름을 딴 칼라일 원은 2차 방정식의 해가 원과 수평축의 교차점의 수평 좌표라는 성질을 가지고 있습니다.^[39]칼라일 원은 규칙적인 다각형의 자와 나침반 구조를 개발하는 데 사용되었습니다.

이차방정식의 일반화

만약 계수 a, b, c가 복소수이거나 더 일반적으로 특성이 2가 아닌 어떤 장의 멤버라면 공식과 그 유도는 여전히 정확합니다. (특성 2의 장에서, 원소 2a는 0이고 그것으로 나누는 것은 불가능합니다.)

기호를

${\displaystyle \pm {\sqrt {b^{2}-4ac}}$

공식에서 "만약 그러한 원소가 존재한다면, 제곱이² b - 4ac인 두 원소 중 하나"로 이해되어야 합니다.일부 필드에는 제곱근이 없는 원소도 있고 2개인 원소도 있습니다. 특성 2의 필드를 제외하고는 0만 제곱근이 하나뿐입니다.필드에 어떤 숫자의 제곱근이 포함되어 있지 않더라도 항상 이를 포함하는 2차 확장 필드가 존재하므로 2차 공식은 항상 해당 확장 필드의 공식으로 의미가 있습니다.

특징2

특성 2의 필드에서 2가 단위가 되는 것에 의존하는 2차 공식은 성립하지 않습니다.단사 이차 다항식을 고려합니다.

${\displaystyle x^{2}+bx+c}$

특성 2의 필드를 넘습니다.b = 0이면 제곱근을 추출하는 것으로 감소하므로 다음과 같습니다.

${\displaystyle x={\sqrt {c}}$

그리고 그 이후로 단 하나의 뿌리가 있습니다.

${\displaystyle -{\sqrt {c}}=-{\sqrt {c}}+2{\sqrt {c}}={\sqrt {c}}}$

정리하자면,

${\displaystyle \displaystyle x^{2}+c=(x+{\sqrt {c}})^{2}}$

유한 필드에서 제곱근을 추출하는 방법에 대한 자세한 내용은 이차 잔차를 참조하십시오.

b가 0인 ≠의 경우, 두 개의 뚜렷한 근이 존재하지만 다항식이 축소 불가능하다면 계수장에 있는 수들의 제곱근으로 표현할 수 없습니다.대신, c의 2-근 R(c)을 다항식² x + x + c의 근으로 정의하고, 이 다항식의 분할 필드의 요소입니다.R(c) + 1도 루트임을 확인합니다.2근 연산의 관점에서, (비모닉) 2차축² + bx + care의 2근은

${\displaystyle {\frac {b}{a}}R\left({\frac {ac}{b^{2}}}\right)}$

그리고.

${\displaystyle {\frac {b}{a}}\left(R\left({\frac {ac}{b^{2}}}\right)+1\right)}$

예를 들어, a가 F의₄ 단위 그룹의 곱셈 생성기, 즉 순서 4의 갈루아 필드(따라서 a와 a + 1은 F에₄ 대한 x² + x + 1의 근입니다)를 나타낸다고 하자.(a + 1) = a이므로, a + 1은 2차 방정식 x + a = 0의 유일한 해입니다.반면, 다항식² x + ax + 1은 F에₄ 대해 축소할 수 없지만, F에₁₆ 대해 분할되며, 여기서 두 개의 근 ab와 ab + a를 가지며, 여기서 b는₁₆ F에서² x + x + a의 근입니다.

이것은 아르틴-슈라이어 이론의 특별한 경우입니다.

참고 항목

• 연속된 분수로 2차 방정식 풀기
• 일차방정식
• 입방함수
• 사중방정식
• 5차방정식
• 대수학의 기본 정리

참고문헌

외부 링크

• "Quadratic equation", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Weisstein, Eric W. "Quadratic equations". MathWorld.
• Wayback Machine에서 2차 방정식 101개 사용 2007-11-10 보관
• 2차 방정식의 101가지 용도: Part II Wayback Machine에서 2007-10-22 보관