옥토미노

Octomino
오토미노와 혼동하지 말 것.
369 무료 옥토미노

옥토미노(또는 8-미노)는 [1]8차 폴리오미노, 즉 모서리끼리 연결된 8개의 동일한 크기의 정사각형으로 구성된 평면 내 폴리곤입니다.회전과 반사가 뚜렷한 모양으로 간주되지 않을 경우 369개의 다른 자유 옥토미노가 있습니다.반사를 구별하는 것으로 간주할 때, 704개의 단측 옥토미노가 있다.회전도 구별되는 것으로 간주할 때 2,725개의 고정 [2][3]옥토미노가 있습니다.

대칭

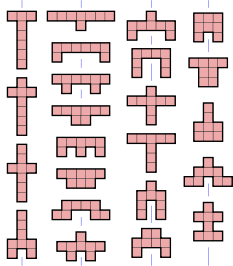
그림에는 대칭 그룹에 따라 색칠된 가능한 모든 자유 옥토미노가 나와 있습니다.

  • 316 옥토미노(회색)는 대칭이 없습니다.대칭 그룹은 오직 아이덴티티 매핑으로만 구성됩니다.
  • 23 옥토미노(빨간색)는 격자선에 정렬된 반사 대칭 축을 가진다.대칭 그룹에는 정사각형의 변에 평행한 선의 동일성과 반사라는 두 가지 요소가 있습니다.
Reflection symmetrical octominoes 90 deg.svg
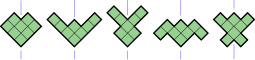
  • 5 옥토미노(녹색)는 격자선에 대해 45°의 반사 대칭 축을 가진다.대칭 그룹에는 동일성과 대각선 반사라는 두 가지 요소가 있습니다.
Reflection symmetrical octominoes 45 deg.svg
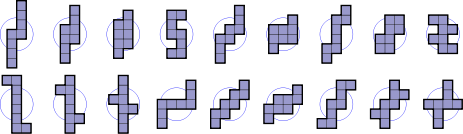
  • 18개의 옥토미노(파란색)는 2차 회전 대칭이라고도 하는 점 대칭을 가집니다.대칭 그룹에는 항등식과 180° 회전이라는 두 가지 요소가 있습니다.
Rotation symmetrical octominoes (C2).svg
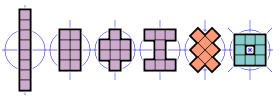
  • 1 옥토미노(노란색)는 순서 4의 회전 대칭을 가집니다.대칭 그룹에는 4개의 요소가 있습니다. 즉, 동일성과 90°, 180° 및 270° 회전입니다.
Rotation symmetrical octomino (C4).svg
  • 4 옥토미노(자주색)에는 두 개의 반사 대칭 축이 있으며 둘 다 격자선과 정렬됩니다.대칭 그룹에는 4개의 요소, 즉 동일성, 2개의 반사 및 180° 회전이 있습니다.클라인 4군이라고도 하는 2차 2면체 군입니다.
  • 1 옥토미노(주황색)에는 대각선과 정렬된 두 개의 반사 대칭 축이 있습니다.대칭군은 또한 4개의 원소가 있는 2차 2면체 군이다.
  • 1 옥토미노(시안)는 격자선과 대각선에 정렬된 4개의 반사 대칭 축과 순서 4의 회전 대칭을 가지고 있습니다.대칭군인 4차 2면체 그룹은 8개의 원소를 가지고 있다.
Rotation and reflection symmetric octominoes h.svg

옥토미노 세트는 가능한 8개의 대칭이 모두 실현되는 가장 낮은 폴리미노 세트입니다.다음으로 이 속성을 가진 상위 세트는 dodecomino(12-mino) [3]세트입니다.

옥토미노의 반사가 일면 옥토미노와 같이 구별되는 것으로 간주될 경우, 첫 번째, 네 번째 및 다섯 번째 범주는 크기가 두 배로 증가하여 총 704개의 옥토미노가 추가로 335개 생성됩니다.회전도 구별되는 것으로 간주되면 첫 번째 카테고리의 옥토미노는 8배, 다음 세 카테고리의 옥토미노는 4배, 다섯 번째 카테고리에서 일곱 번째 옥토미노는 두 번, 마지막 옥토미노는 한 번만 계산됩니다.그 결과 316 × 8 + (23+5+18) × 4 + (1+4+1) × 2 + 1 = 2,725 고정 옥토미노가 된다.

포장 및 타일링

369개의 자유 옥토미노 중 320개가 Conway 기준을 충족하고 23개가 [4]더 기준을 충족하는 패치를 형성할 수 있습니다.나머지 26개의 옥토미노(구멍이 있는 6개 포함)는 [5]평면을 테셀링할 수 없습니다.

자유 옥토미노 중 6개는 구멍이 있기 때문에 옥토미노 전체를 직사각형 안에 넣을 수 없고 모든 옥토미노를 타일링할 수 없다는 것을 증명하는 것은 간단하다.

Octominoes with holes.svg

레퍼런스

  1. ^ Golomb, Solomon W. (1994). Polyominoes (2nd ed.). Princeton, New Jersey: Princeton University Press. ISBN 0-691-02444-8.
  2. ^ Weisstein, Eric W. "Octomino". From MathWorld – A Wolfram Web Resource. Retrieved 2008-07-22.
  3. ^ a b Redelmeier, D. Hugh (1981). "Counting polyominoes: yet another attack". Discrete Mathematics. 36 (2): 191–203. doi:10.1016/0012-365X(81)90237-5.
  4. ^ Rhoads, Glenn C. (2005). "Planar tilings by polyominoes, polyhexes, and polyiamonds". Journal of Computational and Applied Mathematics. 174 (2): 329–353. doi:10.1016/j.cam.2004.05.002.
  5. ^ Gardner, Martin (August 1975). "More about tiling the plane: the possibilities of polyominoes, polyiamonds and polyhexes". Scientific American. 233 (2): 112–115.