허블의 법칙

허블의 법칙, 일명 허블-레마 î트레 법칙은 물리우주론에서 은하가 거리에 비례하는 속도로 지구로부터 멀어지고 있다는 관측입니다. 즉, 그들이 멀리 있을수록, 그들은 지구로부터 더 빨리 멀어지고 있다는 것입니다. 은하의 속도는 가시 스펙트럼의 적색 끝을 향해 방출되는 빛의 이동인 적색편이에 의해 결정되었습니다.

허블의 법칙은 우주의 팽창에 대한 최초의 관측 기반으로 여겨지며, 오늘날 빅뱅 모형을 뒷받침하는 가장 자주 인용되는 증거 중 하나로 작용하고 있습니다.^[2]^[3] 이러한 팽창에 의한 천체의 운동만을 허블 흐름이라고 합니다.^[4] 그것은 이동 거리와 달리 시간에 따라 변할 수 있는 은하까지의 "적당한 거리" D와 우주론적 시간 좌표에 대한 적절한 거리의 도함수 사이의 비례 상수인 H와 함께 방정식 v = HD로 설명됩니다. (이 속도 정의의 미묘한 부분에 대한 자세한 내용은 이동 및 적절한 거리 § 적절한 거리 사용을 참조하십시오.)

허블 상수는 (km/s)/Mpc에서 가장 자주 인용되므로 1메가파섹(3.09×10km¹⁹) 떨어진 은하의 km/s 속도를 제공하며, 그 값은 약 70(km/s)/Mpc입니다. 그러나 단위를 빼면 H가 주파수(SI₀ 단위: s) 단위이며⁻¹ H의 역수는₀ 허블 시간으로 알려져 있습니다. 허블 상수는 상대적인 팽창 속도로 해석될 수도 있습니다. 이 형태에서 H = 7%/Gyr은 현재의 확장 속도에서 결합되지 않은 구조가 7% 성장하는 데 10억 년이 걸린다는 것을 의미합니다.

에드윈 허블에게 널리 알려져 있지만 계산 ^[5]^[6]^[7]가능한 속도로 팽창하는 우주의 개념은 1922년 알렉산더 프리드만에 의해 일반 상대성 이론에서 처음 도출되었습니다. 프리드만은 현재 프리드만 방정식으로 알려진 일련의 방정식을 발표하여 우주가 팽창하고 있을 수 있다는 것을 보여주었고, 그렇다면 팽창 속도를 제시했습니다.^[8] 그 후 1927년 조르주 르마 î트르는 독립적으로 우주가 팽창하고 있을 수 있다는 것을 도출하고, 멀리 떨어진 물체의 수축 속도와 거리 사이의 비례성을 관찰하여 비례 상수에 대한 추정 값을 제시했습니다. 이 상수는, 에드윈 허블이 우주 팽창의 존재를 확인하고 2년 후 더 정확한 값을 결정했을 때, 그의 이름은 허블 상수로 알려지게 되었습니다.^[2]^[9]^[10]^[11]^[12] 허블은 적색편이로부터 물체의 후퇴 속도를 추론했는데, 이들 중 많은 것들은 1917년 베스토 슬립허에 의해 초기에 측정되었고 속도와 관련이 있었습니다.^[13]^[14]^[15] 허블 상수 H는₀ 주어진 순간에 일정하지만 허블 상수가 현재 값인 허블 파라미터 H는 시간에 따라 변하므로 상수라는 용어는 다소 잘못된 이름으로 여겨지기도 합니다.^[16]^[17]

디스커버리

허블이 관측하기 10년 전, 많은 물리학자들과 수학자들은 일반 상대성 이론의 아인슈타인 장 방정식을 사용하여 팽창하는 우주에 대한 일관된 이론을 확립했습니다. 우주의 본질에 가장 일반적인 원리를 적용하면 정적 우주라는 당시 일반적인 개념과 상충되는 동적인 해결책이 도출되었습니다.

Slipher 관측치

1912년 베스토 M. Slipher는 "나선 성운"의 첫 번째 도플러 이동을 측정했고, 곧 그러한 성운들이 거의 모두 지구에서 멀어지고 있다는 것을 발견했습니다. 그는 이 사실의 우주론적 의미를 파악하지 못했고, 실제로 그 당시 이 성운들이 은하수 밖의 "섬 우주"인지 아닌지에 대해서는 큰 논란이 있었습니다.^[19]^[20]

FLRW 방정식

1922년, 알렉산더 프리드만은 아인슈타인의 장방정식에서 프리드만 방정식을 유도하여 우주가 방정식으로 계산 가능한 속도로 팽창할 수 있음을 보여주었습니다.^[21] 프리드만이 사용한 매개변수는 오늘날 척도 인자로 알려져 있으며 허블 법칙의 비례 상수의 척도 불변 형태로 간주될 수 있습니다. 조르주 르마 î트르는 1927년 다음 절에서 논의한 논문에서 비슷한 해결책을 독자적으로 발견했습니다. 프리드만 방정식은 균일하고 등방성인 우주에 대한 메트릭을 주어진 밀도와 압력을 가진 유체에 대한 아인슈타인의 필드 방정식에 삽입함으로써 유도됩니다. 팽창하는 시공간에 대한 이 아이디어는 결국 우주론의 빅뱅 이론과 정상 상태 이론으로 이어질 것입니다.

레마 î트레 방정식

허블이 자신의 논문을 발표하기 2년 전인 1927년, 벨기에의 신부이자 천문학자인 조르주 레마 î트르는 현재 허블의 법칙으로 알려진 것을 유도하는 연구를 처음으로 발표했습니다. 캐나다 천문학자 시드니 반 덴 버그(Sydney van den Bergh)에 따르면, " 1927년 레마 î트르에 의한 우주 팽창의 발견은 충격이 적은 저널에 프랑스어로 출판되었습니다. 1931년 이 기사의 고영향 영어 번역에서, 현재 허블 상수라고 알려진 것에 대한 언급을 생략함으로써 임계 방정식이 변경되었습니다."^[22] 번역된 논문의 변경은 현재 르마 î트르가 직접 수행한 것으로 알려졌습니다.

우주의 모양

현대 우주론이 등장하기 전에는 우주의 크기와 모양에 대한 상당한 이야기가 있었습니다. 1920년, 샤플리-커티스 논쟁은 Harlow Shapley와 Heber D 사이에 벌어졌습니다. 이 문제로 커티스. 샤플리는 은하수 크기의 작은 우주를 주장했고 커티스는 우주가 훨씬 크다고 주장했습니다. 이 문제는 허블의 향상된 관측으로 다음 10년 안에 해결되었습니다.

세페이드 변광성 우리은하 바깥쪽

에드윈 허블은 당시 세계에서 가장 강력한 망원경이 있는 ^[24]윌슨 산 천문대에서 대부분의 전문적인 천문 관측 작업을 수행했습니다. 그는 세페이드 변광성들을 "나선 성운"에서 관측함으로써 이 천체들까지의 거리를 계산할 수 있었습니다. 놀랍게도, 이 물체들은 은하수 밖에 있는 거리에 있는 것으로 밝혀졌습니다. 그것들은 계속해서 성운이라고 불렸고, 은하라는 용어가 그것을 대체한 것은 겨우 점진적이었습니다.

거리 측정에 적색 쉬프트 결합

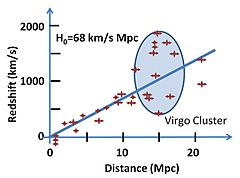
허블의 법칙에 등장하는 매개변수인 속도와 거리는 직접 측정되지 않습니다. 실제로 우리는 거리에 대한 정보를 제공하는 초신성 밝기와 방사선 스펙트럼의 적색편이 z = ∆λ/ λ를 결정합니다. 허블은 밝기와 매개변수 z를 상관시켰습니다.

그의 은하 거리 측정과 베스토 슬립허 및 밀턴 휴메이슨의 은하와 관련된 적색편이 측정을 결합하여 허블은 물체의 적색편이와 거리 사이의 대략적인 비례성을 발견했습니다. 비록 상당한 산란(현재는 특이한 속도에 의해 발생하는 것으로 알려져 있음)이 있었지만, '허블 흐름'은 후퇴 속도가 국소적인 특이한 속도보다 클 정도로 충분히 먼 공간 영역을 지칭하는 데 사용됩니다. 허블은 자신이 연구한 46개의 은하에서 추세선을 그려 500(km/s)/Mpc의 허블 상수 값을 얻을 수 있었습니다. (거리 보정의 오류로 인해 현재 허용되는 값보다 훨씬 높습니다. 자세한 내용은 우주 거리 사다리를 참조하십시오.)

허블도

허블의 법칙은 관측자와의 거리에 대해 물체의 속도(적색 이동에 대략 비례한다고 가정)를 표시한 "허블 도표"에서 쉽게 묘사될 수 있습니다.^[28] 이 도표에서 양의 기울기의 직선은 허블의 법칙을 시각적으로 묘사한 것입니다.

우주상수 포기

허블의 발견이 발표된 후, 알버트 아인슈타인은 우주 상수에 대한 그의 연구를 포기했습니다. 그는 일반 상대성 이론의 방정식을 수정하여 정적인 해를 만들 수 있도록 설계했고, 우주의 올바른 상태라고 생각했습니다. 가장 단순한 형태의 아인슈타인 방정식들은 팽창하거나 수축하는 우주를 모델로 삼기 때문에, 아인슈타인의 우주상수는 완벽한 정적이고 평평한 우주를 얻기 위해 팽창 또는 수축에 대항하기 위해 인위적으로 만들어졌습니다.^[29] 사실 우주가 팽창하고 있다는 허블의 발견 이후, 아인슈타인은 우주가 정적이라는 잘못된 가정을 "가장 큰 실수"라고 불렀습니다.^[29] 그 자체로, 일반 상대성 이론은 우주의 팽창을 예측할 수 있었는데, 이는 (큰 질량에 의한 빛의 휘어짐이나 수성 궤도의 세차와 같은 관측을 통해) 실험적으로 관찰할 수 있었고, 그가 원래 공식화했던 방정식의 특정 해를 사용하여 그의 이론적 계산과 비교할 수 있었습니다.

1931년, 아인슈타인은 현대 우주론의 관측 기반을 제공해 준 허블에게 감사하기 위해 윌슨 산 천문대로 갔습니다.^[30]

우주 상수는 암흑 에너지에 대한 가상적인 설명으로 최근 수십 년 동안 다시 주목을 받고 있습니다.^[31]

해석

단순한 선형 관계 v = cz; 일반 상대성 이론과 관련된 다양한 가능한 모양; 특수 상대성 이론에 따라 빛보다 더 빠른 속도를 허용하지 않는 곡선을 포함한 다양한 가능한 리세스 속도 대 적색편이 함수. 모든 곡선은 낮은 적색 이동에서 선형입니다. 데이비스와 라인위버를 참조하세요.^[32]

적색편이와 거리 사이의 선형 관계에 대한 발견은 열성 속도와 적색편이 사이의 추정된 선형 관계와 결합되어 허블의 법칙에 대한 간단한 수학적 표현을 다음과 같이 산출합니다.

v=H_{0}\,D

어디에

$v$ $v$ 은 $v$ 일반적으로 km/s로 표시되는 리세스 속도입니다.
그의₀ 허블 상수는 H ${\displaystyle$ H $}$ 의 값에 해당하며, $H$ 첨자 0으로 표시된 관측 시점에 취해진 프리드만 방정식에서 H {\displaystyle H}(흔히 시간에 의존하고 척도 인자의 관점에서 표현될 수 있는 값인 허블 매개 변수라고 함)에 해당합니다. 이 값은 주어진 이동 시간 동안 우주 전체에서 동일합니다.
$D$ $D$ 는 $D$ 주어진 우주 시간에 의해 정의된 3-공간에서 은하에서 관측자까지의 이동 거리(일정한 이동 거리와 달리 시간에 따라 변할 수 있음)입니다. (불응 속도는 v = dD/dt에 불과합니다.)

허블의 법칙은 후퇴 속도와 거리 사이의 근본적인 관계로 여겨집니다. 그러나 열성 속도와 적색편이 사이의 관계는 채택된 우주론적 모델에 따라 다르며 작은 적색편이를 제외하고는 확립되지 않습니다.

허블 구면의_HS 반지름보다 큰 거리 D의 경우, 물체는 빛의 속도보다 빠른 속도로 물러납니다(이에 대한 중요성에 대한 논의는 적절한 거리 사용 참조).

r_{\text}HS}}={\frac {c}{H_{0}}\ .

허블 "상수"는 시간이 아닌 공간에서만 상수이기 때문에, 허블 구의 반지름은 다양한 시간 간격에 따라 증가하거나 감소할 수 있습니다. 첨자 '0'은 오늘날 허블상수의 값을 나타냅니다.^[25] 현재의 증거는 우주의 팽창이 가속화되고 있다는 것을 암시합니다(우주 가속 참조). 즉, 은하가 점점 더 먼 거리로 이동함에 따라 후퇴 속도 dD/dt가 시간이 지남에 따라 증가한다는 것을 의미합니다. 그러나 허블 매개변수는 실제로 시간이 지남에 따라 감소하는 것으로 생각됩니다. 만약 우리가 어떤 고정된 거리 D를 보고 일련의 다른 은하들이 그 거리를 지나가는 것을 본다면, 나중의 은하들은 이전의 은하들보다 더 작은 속도로 그 거리를 지나갈 것이라는 것을 의미합니다.^[33]

적색편이속도와 열성속도

적색편이는 원거리 퀘이사에 대한 수소 α선과 같은 알려진 전이의 파장을 결정하고 정지된 기준과 비교하여 분수 이동을 찾음으로써 측정할 수 있습니다. 따라서 적색편이는 실험적 관찰을 위해 모호하지 않은 양입니다. 적색편이와 열성속도의 관계는 또 다른 문제입니다. 광범위한 토론은 해리슨을 참조하세요.^[34]

적색편이속도

적색편이 z는 종종 적색편이 속도로 설명되는데, 이 속도는 선형 도플러 효과에 의해 발생할 경우 동일한 적색편이를 생성하는 리세스 속도입니다(그러나 이 속도는 우주론적 팽창에 의해 부분적으로 발생하기 때문에 그렇지 않습니다). 그리고 관련된 속도가 너무 커서 도플러 이동에 대해 비상대론적 공식을 사용할 수 없기 때문입니다. 이 적색편이 속도는 빛의 속도를 쉽게 초과할 수 있습니다.^[35] 즉, 적색편이속도 v를_rs 결정하기 위해서는 다음과 같은 관계가 있습니다.

v_{\text{rs}}\equiv cz,

사용합니다.^[36]^[37] 즉, 적색편이 속도와 적색편이 사이에는 근본적인 차이가 없습니다. 그들은 엄격하게 비례하며 어떤 이론적 추론으로도 관련이 없습니다. "적색 이동 속도" 용어의 배경에는 적색 이동 속도가 소위 피조-도플러 공식의 낮은 속도 단순화에서 오는 속도와 일치하기 때문입니다.^[38]

z={\frac {\lambda _{\text{o}}}{\lambda _{\text{e}}-1={\sqrt {\frac {1+{\frac {v}{c}}{1-{\frac {v}}-1\approx {\frac {v}}-1

여기서 λ, λ은 각각 관측 파장과 방출 파장입니다. 그러나 "적색 이동 속도" v는_rs 더 큰 속도에서 실제 속도와 단순하게 관련되지 않으며, 이 용어는 실제 속도로 해석될 경우 혼란을 초래합니다. 다음으로 적색편이 또는 적색편이 속도와 열성 속도 사이의 연관성에 대해 설명합니다. 이 토론은 Sartori를 기반으로 합니다.^[39]

후퇴속도

R(t)를 우주의 척도 인자라고 하고 선택한 우주 모형에 따라 우주가 팽창함에 따라 증가한다고 가정합니다. 이는 측정된 모든 적절한 거리 D(t)가 R에 비례하여 증가한다는 것을 의미합니다. (공진점은 공간이 팽창한 결과를 제외하고는 서로 상대적으로 움직이지 않습니다.) 다른 말로 하면:

{\frac {D(t)}{D(t_{0})}}={\frac {R(t)}{R(t_{0})}},

여기서 t는₀ 약간의 기준 시간입니다.^[40] 만약 시간_e t에 은하계에서 빛이 방출되어 우리에게₀ 수신된다면, 우주의 팽창으로 인해 적색편이가 일어나는데, 이 적색편이 z는 간단히 다음과 같습니다.

z={\frac {R(t_{0})}{R(t_{\text{e}})}}-1.

은하가 거리 D에 있고, 이 거리가 시간에 따라 속도 dD로_t 변한다고 가정해 보겠습니다. 우리는 이 불황 속도를 "불황 속도" v라고_r 부릅니다.

v_{\text{r}}=d_{t}D={\frac {d_{t}R}{R}}D.

우리는 이제 허블 상수를 다음과 같이 정의합니다.

H\equiv {\frac {d_{t}R}{R}},

그리고 허블 법칙을 발견합니다.

v_{\text{r}}=HD.

이러한 관점에서 볼 때, 허블의 법칙은 (i) 공간의 팽창에 의해 기여된 오목 속도와 (ii) 물체까지의 거리 사이의 근본적인 관계이며, 적색편이와 거리 사이의 연결은 허블의 법칙과 관측을 연결하는 데 사용되는 목발입니다. 이 법칙은 테일러 급수를 확장함으로써 대략적으로 적색편이 z와 연관될 수 있습니다.

z={\frac {R(t_{0})}{R(t_{e})}}-1\approx {\frac {R(t_{0})}{R(t_{0})\left(1+(t_{e}-t_{0})H(t_{0})\right)}}-1\approx (t_{0}-t_{e})H(t_{0}),

거리가 너무 크지 않으면 모형의 다른 모든 복잡성은 작은 보정이 되며 시간 간격은 단순히 거리를 빛의 속도로 나눈 값입니다.

z\approx (t_{0}-t_{\text{e}})H(t_{0})\approx {\frac {D}{c}}H(t_{0}),

아니면

cz\approx DH(t_{0})=v_{r}

이 접근법에 따르면 cz = v 관계는 낮은 적색편이에서 유효한 근사치이며, 모델 의존적인 큰 적색편이에서 관계로 대체됩니다. 속도 적색편이 그림을 참조하십시오.

파라미터의 관측가능성

엄밀히 말하면 공식에서 v나 D는 직접 관측할 수 없습니다. 왜냐하면 그것들은 현재 은하의 속성이기 때문입니다. 반면에 우리의 관측은 현재 우리가 보는 빛이 은하를 떠난 과거의 은하를 가리킵니다.

상대적으로 가까운 은하(단일성보다 훨씬 작은 reds편 z)의 경우 v와 D는 크게 변하지 않을 것이며, $v=zc$ 는 $v=zc$ v = $v=zc$ z c ${\$ displaystyle v=zc}를 사용하여 추정할 수 있습니다. 여기서 c는 빛의 속도입니다. 이것은 허블에 의해 발견된 경험적 관계를 제공합니다.

먼 은하의 경우 시간에 따라 H가 어떻게 변하는지에 대한 상세한 모델을 지정하지 않고는 z로부터 v(또는 D)를 계산할 수 없습니다. 적색편이는 빛이 시작될 때의 후퇴 속도와도 직접적인 관련이 없지만, 광자가 관측자를 향해 이동하는 동안 우주가 팽창한 요인은 (1 + z)라는 간단한 해석이 있습니다.

팽창 속도 대 고유 속도

허블의 법칙을 이용하여 거리를 결정할 때에는 우주의 팽창에 의한 속도만을 사용할 수 있습니다. 중력으로 상호작용하는 은하들은 우주의 팽창과는 무관하게 서로 상대적으로 움직이기 때문에,^[41] 이러한 상대적인 속도들을 허블의 법칙을 적용할 때 설명할 필요가 있습니다. 이러한 특이한 속도는 적색편이 공간 왜곡을 일으킵니다.

허블 매개변수의 시간 의존성

매개변수 $H$ ${\displaystyle$ H $}$ 는 일반적으로 "허블 상수"라고 $H$ 불리지만, 이는 고정된 시간에만 공간에서 일정하기 때문에 잘못된 이름입니다. 거의 모든 우주 모형에서 시간에 따라 달라지며, 먼 물체에 대한 모든 관측도 "상수"가 다른 값을 가졌던 먼 과거로의 관측입니다. $H_{0}$ {\ $displaystyle H_{0}}$ 이 $H_{0}$ 현재 값을 나타내는 "Hubble 파라미터"가 더 정확한 용어입니다 $.$

또 다른 일반적인 혼란의 원인은 가속하는 우주가 시간에 따라 허블 매개변수가 실제로 증가한다는 것을 의미하지 않는다는 것입니다. $($ 는 $H(t)\equiv {\dot {a}}(t)/a(t)$ ˙ $t)$ / $a(t$ ) ${\displaystyle H(t$ equiv {\dot {a}}(t)/a(t)}, 대부분의 가속 $모델$ 에서 ${\displaystyle$ $a$ $}$ 는 ˙ ${\displaystyle$ dot {a}}보다 상대적으로 빠르게 증가하므로 H는 시간에 따라 감소합니다. (선택된 한 은하의 후퇴 속도는 증가하지만, 고정된 반지름의 구를 지나는 다른 은하들은 나중에 더 천천히 구를 가로지릅니다.)

$무차원$ 감속 파라미터 ${\textstyle q\equiv -{\frac {{\ddot {a}}\,a}{{\dot {a}}^{2}}}}$ ≡ - ¨ ${\textstyle q\equiv -{\frac {{\ddot {a}}\,a}{{\dot {a}}^{2}}}}$ a ˙ $2 {\textstyle q\equiv$ - ${\frac{\dot$ {a ${\textstyle q\equiv -{\frac {{\ddot {a}}\,a}{{\dot {a}}^{2}}}}$ a}{\dot {a}^{2}}를 정의할 때, 다음과 같습니다.

{\frac {dH}{dt}}=-H^{2}(1+q)

$q<-1$ 로부터 허블 $q<-1$ 는 $q<-1$ q < - 1 {\ $displaystyle$ q $<-1}$ 이 아닌 한 시간에 따라 감소하고 있음을 알 수 있습니다 $q<-1$ 후자는 이론적으로 다소 가능성이 없는 것으로 간주되는 우주가 팬텀 에너지를 포함하는 경우에만 발생할 수 있습니다.

그러나 표준 람다 차가운 암흑 물질 모델(람다-CDM 또는 λCDM $모델$ )에서 q {\displaystyle q}는 우주 상수가 물질보다 점점 더 우세해짐에 따라 먼 미래에 위에서 -1로 가는 경향이 있을 것입니다. 이는 H ${\displaystyle$ H}가 위에서 ≈ 57(km/s)/Mpc의 일정한 값으로 접근한다는것을 $H$ 합니다. 그러면 우주의 규모 계수는 시간이 지남에 따라 기하급수적으로 증가할 것입니다.

이상화된 허블의 법칙

균일하게 팽창하는 우주에 대한 이상화된 허블의 법칙의 수학적 유도는 3차원 데카르트/뉴턴 좌표 공간에서 기하학의 상당히 기본적인 정리이며, 메트릭 공간으로 간주되며 완전히 균질하고 등방성(특성은 위치나 방향에 따라 변하지 않음)입니다. 간단히 말해서 정리는 다음과 같습니다.

직선을 따라 그리고 원점에서 거리에 비례하는 속도로 원점에서 멀어지는 모든 두 점은 거리에 비례하는 속도로 서로 멀어질 것입니다.

사실 이것은 비데카르트 공간, 특히 우주론적 모델로 자주 고려되는 음의 곡선과 양의 곡선 공간에 대해 국부적으로 균질하고 등방성인 경우에만 적용됩니다(우주의 모양 참조).

이 정리에서 비롯된 관찰은 지구에서 물체가 우리로부터 멀어지는 것을 보는 것이 지구가 팽창이 일어나는 중심에 가까이 있다는 표시가 아니라 팽창하는 우주의 모든 관찰자가 물체로부터 멀어지는 것을 볼 것이라는 것입니다.

우주의 궁극적인 운명과 나이

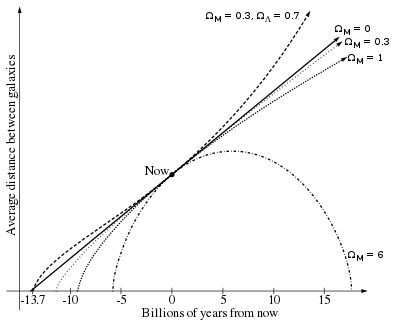
허블 파라미터의 값은 시간이 지남에 따라 변하며 $q$ 다음에 의해 정의되는 이른바 감속 파라미터 $q$ $q$ 의 값에 따라 증가하거나 감소합니다.

{\displaystyle q=-\left(1+{\frac {\dot {H}}{H^{2}}\right).

감속 파라미터가 0인 우주에서는 H = 1/t, 여기서 t는 빅뱅 이후의 시간입니다. $q$ 이 아닌 시간 의존적인 q {\displaystyle $q}$ 값은 단순히 $q$ 현재 시간에서 이동하는 지평선 크기가 0이었던 시간까지 프리드만 방정식을 역방향으로 통합해야 합니다.

중력의 인력으로 인해 팽창이 둔화되고 있음을 나타내는 q가 양의 값을 갖는다고 오랫동안 생각되어 왔습니다. 이것은 1/H(약 140억 년) 미만의 우주의 나이를 의미합니다. 예를 들어, q의 값이 1/2이면 (한때 대부분의 이론가들이 선호했던) 우주의 나이는 2/(3H)가 됩니다. 1998년에 q가 분명히 음이라는 것이 발견되었다는 것은 우주가 실제로는 1/H보다 더 오래된 것일 수 있다는 것을 의미합니다. 하지만 우주의 나이에 대한 추정치는 1/H에 매우 가깝습니다.

올버스의 역설

허블의 법칙에 대한 빅뱅의 해석에 의해 요약된 우주의 팽창은 올버스의 역설로 알려진 오래된 수수께끼와 관련이 있습니다. 우주가 크기가 무한하고 정적이며 균일한 별들의 분포로 가득 차 있다면, 하늘의 모든 시선은 별 위에서 끝날 것이고 하늘은 별의 표면처럼 밝을 것입니다. 하지만 밤하늘은 대체로 어둡습니다.^[42]^[43]

17세기 이래로 천문학자들과 다른 사상가들은 이 역설을 해결하기 위해 가능한 많은 방법들을 제안해 왔지만, 현재 받아들여지는 해결책은 부분적으로는 빅뱅 이론에, 부분적으로는 허블 팽창에 달려 있습니다: 유한한 시간 동안 존재했던 우주에서, 오직 유한한 수의 별빛만이 우리에게 도달할 충분한 시간을 가졌고, 역설은 해결되었습니다. 또한 우리로부터 멀리 떨어져 있는 물체들이 멀리 떨어져 나가므로, 우리가 볼 때까지 그 물체들로부터 발산된 빛이 적색편이되어 밝기가 감소하게 됩니다.^[42]^[43]

무차원 허블상수

일반적인 관행은 허블의 상수를 다루는 대신, 일반적으로 h로 표시되고 일반적으로 "작은 h"로 표시되는 무차원 허블 상수를 도입한 다음, 허블의 상수 H를 h × 100 km ⋅ ⋅Mpc로 작성하고 H의 실제 값에 대한 모든 상대적 불확실성을 h로 강등하는 것입니다. 무차원 허블상수는 적색편이 z로부터 계산된 거리를 d ≈ c/H × z로 나타낼 때 자주 사용됩니다. H는 정확히 알려져 있지 않기 때문에 거리는 다음과 같이 표시됩니다.

cz/H_{0}\approx (2998\times z){\text{Mpc}}h^{-1}

즉, 하나는 2998xz를 계산하고 하나는 단위를 ${\text{Mpc }}h^{-1}$ - ${\text{Mpc }}h^{-1}$ 1 {\ $displaystyle$ {\ $text{Mpc}}h^{-1}$ 또는 ${\text{Mpc }}h^{-1}$ $h^{-1}{\text{ Mpc}}.$ - $h^{-1}{\text{Mpc}$ 로 제공합니다.

때때로 100 이외의 기준 값을 선택할 수도 있는데, 이 경우에는 혼란을 피하기 위해 h 뒤에 첨자가 표시됩니다. 예를 들어 h는 $H_{0}=70\,h_{70}\,\mathrm {km{\cdot }s^{-1}{\cdot }Mpc^{-1}}$ 0 = $H_{0}=70\,h_{70}\,\mathrm {km{\cdot }s^{-1}{\cdot }Mpc^{-1}}$ h $H_{0}=70\,h_{70}\,\mathrm {km{\cdot }s^{-1}{\cdot }Mpc^{-1}}$ $km$ ⋅ s - 1 ⋅ M p c - 1 {\ $h_{70}=h/0.7$ H_{0} = 70\,h_{70}\,\mathrm {\cdot }s^{-1} {\cdot }Mpc^{-1}, 즉 h 70 $h_{70}=h/0.7$ = h / 0을 의미합니다. $h_{70}=h/0.7$ ${\displaystyle h_{70$ } $h_{70}=h/0.7$ h $/0.7}$ 입니다 $h_{70}=h/0.7$

이는 H에 1.75 × 10(파섹 및 t의 정의에서)을 곱하여 얻은 일반적으로 플랑크 단위로 표현되는 허블 상수의 무차원 값과 혼동되어서는 안 됩니다. 예를 들어 H = 70의 경우 1.2 × 10의 플랑크 단위 버전이 얻어집니다.

팽창 가속도

1998년에 음으로 밝혀진 Ia형 초신성의 표준 촛불 관측에서 측정된 $q$ $q$ {\ $displaystyle$ q $}$ 의 값은 우주의 팽창이 현재 "가속화"^[46]되어 있다는 의미로 많은 천문학자들을 놀라게 했습니다. (허블 인자는 여전히 시간이 지남에 따라 감소하고 있지만, 해석 섹션에서 위에 언급한 바와 같이 다크 에너지 및 λCDM 모델에 대한 기사를 참조하십시오.

허블 매개변수의 유도

프리드만 방정식부터 시작합니다.

H^{2}\equiv \left({\frac {\dot {a}}{a}}\right)^{2}={\frac {8\pi G}{3}}\rho -{\frac {kc^{2}}{a^{2}}}+{\frac {\Lambda c^{2}}{3}},

$H$ 서 H{\ $displaystyle$ H $}$ 는 허블 파라미터,{\ $displaystyle a}$ 는 스케일 팩터, G는 중력 상수, $k$ {\ $display$ k $}$ 는 우주의 정규화된 공간 곡률로 -1, 0 또는 1과 같으며 $\Lambda$ λ ${\displaystyle$ \Lambda }는 우주 상수입니다.

물질이 지배하는 우주(우주 상수 포함)

만약 우주가 물질이 지배적이라면, $\rho$ 의 질량 밀도 $\rho$ ρ {\displaystyle $\rho$ \rho}는 물질만을 포함하는 것으로 간주될 수 있습니다.

\rho =\rho _{m}(a)={\frac {\rho _{m_{0}}}{a^{3}}},

여기서 $\rho _{m_{0}}$ ρ m 0 ${\displaystyle \rho _$ {m_{0}}는 오늘날 물질의 밀도입니다. 프리드만 방정식과 열역학적 원리로부터 우리는 비상대론적 입자에 대해 질량 밀도가 우주의 역부피에 비례하여 감소한다는 것을 알고 있으므로 위의 방정식은 참이어야 합니다. 정의할 수도 있습니다(밀도 파라미터는 $\Omega _{m}$ ω m {\ $displaystyle$ $Omega$ _{m}} 참조).

{\begin{aligned}\rho_{c}&={\frac {3H_{0}^{2}}{8\pi G}};\\\Omega _{m}&\equiv {\frac {\rho _{m_{0}}}{\rho _{c}}}={\frac {8\pi G}{3H_{0}^{2}}}\rho _{m_{0}};\end{aligned}}

그러므로:

\rho = {\rho _{c}\Omega _{m}}{a^{3}

또 정의상으로는

{\begin{aligned}\Omega_{k}&\equiv {\frac {-kc^{2}}{(a_{0}H_{0})^{2}}}\\\Omega _{\Lambda }&\equiv {\frac {\Lambda c^{2}}{3H_{0}^{2}},\end{aligned}

여기서 첨자 0은 오늘의 값을 나타내고 $a_{0}=1$ = $a_{0}=1$ {\ $display$ a_ $a=1/(1+z)$ 0}=1}입니다. 이 모든 것을 이 절의 시작 부분에서 프리드만 방정식에 대입하고 {\display a}를 = 1 / (1 + z) {\display a= 1 / (1 + z)}로 바꾸면 다음과 같습니다.

H^{2}(z)=H_{0}^{2}\left(\Omega _{m}(1+z)^{3}+\Omega _{k}(1+z)^{2}+\Omega _{\Lambda }\right).

물질과 암흑 에너지가 지배하는 우주

만약 우주가 물질이 지배적이고 암흑 에너지가 지배적이라면, 허블 매개변수에 대한 위의 방정식도 암흑 에너지 상태 방정식의 함수가 될 것입니다. 자, 이제.

\rho =\rho _{m}(a)+\rho _{de}(a),

$\rho _{de}$ 서 $\rho _{de}$ ρ드 ${\displaystyle \rho_$ {de}}는 암흑 에너지의 질량 밀도입니다. 정의에 따르면 우주론의 상태 $P=w\rho c^{2}$ 은 P = w $P=w\rho c^{2}$ ρ $P=w\rho c^{2}$ c 2 {\displaystyle P = w\rhoc^{2}}이며, 이것을 시간에 따라 우주의 질량 밀도가 어떻게 진화하는지를 설명하는 유체 방정식에 대입하면 다음과 같습니다.

{\begin{aligned}{\dot {\rho }}+3{\frac {\dot {a}}{a}}\left(\rho +{\frac {P}{c^{2}}}\right)=0;\\{\frac {d\rho }{\rho }}=-3{\frac {da}{a}}(1+w).\end{align}}

w가 상수라면,

\ln {\rho }=-3(1+w)\ln {a};

다음을 암시합니다.

\rho =a^{-3(1+w)}.

따라서 상태방정식 w가 일정한 암흑에너지의 경우 $\rho _{de}(a)=\rho _{de0}a^{-3(1+w)}$ ρ de $\rho _{de}(a)=\rho _{de0}a^{-3(1+w)}$ (a) = $\rho _{de}(a)=\rho _{de0}a^{-3(1+w)}$ ρ $\rho _{de}(a)=\rho _{de0}a^{-3(1+w)}$ de 0 a - 3 (1 + w) {\displaystyle \rho _{de}(a) =\rho _{de0}a^{-3(1 + w)}}입니다. 이를 이전과 같은 방식으로 프리드먼 방정식에 대입하면 공간적으로 평평한 우주를 가정한 k = 0 {\displaystyle k = 0}으로 설정하면, 그런 다음 (우주의 모양 참조)

H^{2}(z)=H_{0}^{2}\left(\Omega _{m}(1+z)^{3}+\Omega _{de}(1+z)^{3(1+w)}\right).

암흑 에너지가 아인슈타인이 도입한 것과 같은 우주 상수에서 비롯된다면 w = $w=-1$ - $w=-1$ ${\$ displaystyle w = - 1}임을 알 수 있습니다. $\Omega _{k}$ 다음 방정식은 $\Omega _{k}$ ω k {\displaystyle $\Omega_{$ k}가 0으로 설정된 상태에서 물질이 지배하는 우주 섹션의 마지막 방정식으로 축소됩니다. 이 경우 초기 암흑 에너지 밀도 $\rho _{de0}$ ρ de 0 ${\displaystyle \rho$ _{de0}}은 다음과 같습니다.

\rho _{de0}={\frac {\Lambda c^{2}}{8\pi G}}

그리고 ω 드 = ω

\Omega _{de}=\Omega _{\Lambda }.

λ

.

{\displaystyle \Omega _{

de

}=\Omega _{\Lambda}}

암흑 에너지가 일정한 상태 방정식 w를 갖지 않는다면,

\rho _{de}(a)=\rho _{de0}e^{-3\int {\frac {da}{a}}\left(1+w(a)\right)},

그리고 이를 해결하려면 $w(a)$ ${\displaystyle$ w $(a)}$ 매개 변수를 지정해야 합니다. 예를 들어 $w(a)=w_{0}+w_{a}(1-a)$ = $w(a)=w_{0}+w_{a}(1-a)$ 0 + wa(1 - a) {\displaystyle w(a) = w_{0} + w_{a}(1-a)}인 경우 다음을 제공합니다.

H^{2}(z)=H_{0}^{2}\left(\Omega _{m}a^{-3}+\Omega _{de}a^{-3\left(1+w_{0}+w_{a}\right)}e^{-3w_{a}(1-a)}\right).

다른 성분들이 배합되었습니다.^[49]^[50]^[51]

허블 상수에서 유도된 단위

허블 타임

허블 상수 $H_{0}$ 0 ${\$ 은 역시간 단위를 가지며 $H_{0}$ , 허블 시간 t는_H 단순히 허블 상수의 역으로 정의됩니다.^[52]

{\displaystyle t_{H}\equiv {\frac {1}{H_{0}}}={\frac {1}{67.8\mathrm {~(km/s)/Mpc} }}=4.55\times 10^{17}\mathrm {~s} =14.4{\text{billion years}}.

이는 약 138억 년에 달하는 우주의 나이와는 조금 다릅니다. 허블 시간은 팽창이 선형이었다면 가질 수 있었던 나이이며, 팽창이 선형이 아니기 때문에 실제 우주 나이와는 다릅니다. 우주의 에너지 함량에 따라 다릅니다(허블 매개변수의 § 유도 참조).

우리는 현재 진공 에너지의 지배력이 증가함에 따라 우주의 팽창이 기하급수적으로 증가하는 시기에 가까워지고 있는 것으로 보입니다. 이 체계에서 허블 매개변수는 일정하고 우주는 허블 시간마다 1배씩 성장합니다.

H\equiv {\frac {\dot {a}}{a}}={\textrm {constant}}\quad \longright 화살표 \quad a\propto e^{Ht}=e^{\frac {t}{t_{H}}}

마찬가지로, 일반적으로 허용되는 2.27⁻¹ Es의 값은 (현재 속도로) 우주가 1초 안에 $e^{2.27}$ $e^{2.27}$ ${\$ e $^{2.27}$ 증가한다는 것을 의미합니다.

오랜 시간에 걸쳐 역학은 위에서 설명한 바와 같이 일반 상대성 이론, 암흑 에너지, 인플레이션 등에 의해 복잡합니다.

허블 길이

허블 길이 또는 허블 거리는 우주론에서 $cH_{0}^{-1}$ 의 단위로, c H 0 - $cH_{0}^{-1}$ {\ $displaystyle cH_{0}^{-1}$ - 빛의 속도에 허블 시간을 곱한 것으로 정의됩니다. $cH_{0}^{-1}$ 이는 4,420만 파섹 또는 144억 광년에 해당합니다. (광년 단위의 허블 길이 수치는 정의상 허블 시간의 수치와 수년 단위의 값과 같습니다.) 허블 거리는 $D=cH_{0}^{-1}$ = $D=cH_{0}^{-1}$ $D=cH_{0}^{-1}$ $D=cH_{0}^{-1}$ - 1 $D=cH_{0}^{-1}$ {\displaystyle D = cH_{0}^{-1}을 허블의 법칙인 v = HD의 방정식에 대입하면 알 수 있듯이 광속으로 현재 우리로부터 멀어지고 있는 지구와 은하 사이의 거리가 됩니다.

허블 부피

허블 부피는 때때로 $cH_{0}^{-1}.$ $cH_{0}^{-1}.$ $cH_{0}^{-1}.$ - $cH_{0}^{-1}.$ 의 결합 크기를 가진 우주의 부피로 정의됩니다 $cH_{0}^{-1}.$ $cH_{0}^{-1}$ 반지름이 $cH_{0}^{-1},$ H $cH_{0}^{-1},$ - $cH_{0}^{-1},$ 구의 부피 $cH_{0}^{-1},$ $cH_{0}^{-1}$ 또는 $cH_{0}^{-1},$ 면 $cH_{0}^{-1}.$ $cH_{0}^{-1}.$ - $cH_{0}^{-1}.$ 의 정육면체로 정의됩니다 $cH_{0}^{-1}.$ $cH_{0}^{-1}.$ $cH_{0}^{-1}$ 어떤 $cH_{0}^{-1}.$ 우주론자들은 심지어 관측 가능한 우주의 부피를 가리키기 위해 허블 부피라는 용어를 사용하기도 하지만, 이 부피는 반지름이 약 3배 더 큽니다.

허블상수 결정

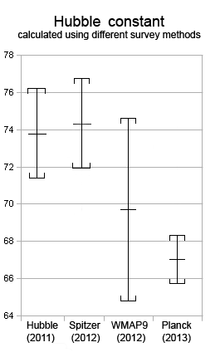
허블 상수의 값은 멀리 떨어진 은하들의 적색편이를 측정한 다음 허블의 법칙이 아닌 다른 방법으로 은하들과의 거리를 측정함으로써 추정됩니다. 이 접근법은 은하 외 물체까지의 거리를 측정하기 위한 우주 거리 사다리의 일부를 형성합니다. 이러한 거리를 결정하는 데 사용되는 물리적 가정의 불확실성으로 인해 허블 상수의 다양한 추정치가 발생했습니다.^[2]

허블 장력

허블 상수를 결정하기 위해 여러 가지 방법이 사용되었습니다. 보정된 거리 사다리 기술을 사용한 "후기 우주" 측정값은 약 73km/s/Mpc의 값에 수렴되었습니다. 2000년 이후 우주 마이크로파 배경 측정을 기반으로 한 "초기 우주" 기술이 사용 가능해졌으며, 이들은 67.7km/s/mpc 근처의 값과 일치합니다. (이는 초기 우주 이후의 팽창률 변화를 설명하는 것이므로 첫 번째 숫자와 유사합니다.) 기법이 개선됨에 따라 추정된 측정 불확실성은 줄어들었지만 측정값의 범위는 불일치가 통계적으로 매우 유의할 정도로 줄어들었습니다. 이 불일치를 허블 장력이라고 합니다.^[54]^[55]

허블 장력 불일치의 원인은 알려지지 않았으며,^[56] 많은 가능한 해결책이 제시되어 있습니다. 가장 보수적인 것은 초기 우주 관측 또는 후기 우주 관측에 영향을 미치는 알려지지 않은 체계적인 오류가 있다는 것입니다. 이 설명은 직관적으로 매력적이지만 초기-우주 관측 또는 후기-우주 관측이 틀리든 상관없이 관련 없는 여러 효과를 필요로 하며 명백한 후보가 없습니다.^[55] 또한 초기-우주 관측과 후기-우주 관측은 모두 다른 망원경에서 나오기 때문에 그러한 체계적인 오류는 여러 다른 기기에 영향을 미칠 필요가 있습니다.^[a]^[b]

또는 관측치가 정확할 수 있지만 일부 원인 불명의 효과로 인해 불일치가 발생하고 있습니다. 우주론적 원리가 실패할 경우("람다-CDM 모델" 기사의 "우주론적 원리 위반" 참조), 허블 상수와 허블 장력에 대한 기존 해석을 수정해야 하며, 이는 허블 장력을 해결할 수 있습니다.^[58] 특히, 우리는 초신성과 중입자 음향 진동 관측과 긴장 관계에 있지 않기 위해 최대 0.5의 적색편이 내에 위치해야 합니다.^[55] 또 다른 가능성은 측정의 불확실성이 과소평가되었을 수 있다는 것입니다.^[59]^[60]

가장 흥미로운 가능성은 λCDM 모델을 넘어서는 새로운 물리학입니다. 일반 상대성 이론을 수정된 뉴턴 역학으로 대체하면 초기 우주의 암흑 에너지 구성 요소,^[61]^[c]^[62] 시간에 따라 변하는 상태 방정식으로 암흑 에너지 또는 암흑 ^[d]^[63]복사로 붕괴되는 암흑 물질과 같이 잠재적으로 긴장을 해결할 수 있습니다.^[64] 이 모든 이론이 직면한 문제는 초기 우주 측정과 후기 우주 측정 모두 여러 독립적인 물리학 라인에 의존하며 다른 곳에서 성공을 보존하면서 이러한 라인 중 어느 것도 수정하기 어렵다는 것입니다. 도전의 규모는 일부 저자들이 새로운 초기 우주 물리학만으로는 충분하지 않다고 주장하는 반면, 다른 저자들은 새로운 후기 우주 물리학만으로는 충분하지 않다고 주장하는 것을 통해 알 수 있습니다.^[65]^[66]^[67] 그럼에도 불구하고, 천문학자들은 허블 장력에 대한 관심이 지난 몇 년 동안 강하게 증가하면서 노력하고 있습니다.^[55]

이전 측정 및 토론 접근 방식

천문학자 Walter Baade의 관찰은 그가 항성에 대한 뚜렷한 "인구"(인구 I과 인구 II)를 정의하도록 이끌었습니다. 같은 관측을 통해 그는 세페이드 변광성에 두 종류가 있다는 사실을 발견했습니다. 이 발견을 이용하여 그는 알려진 우주의 크기를 다시 계산하여 1929년 허블이 계산했던 이전의 두 배로 늘렸습니다.^[68]^[69]^[70] 그는 1952년 로마에서 열린 국제천문연맹 회의에서 이 연구결과를 상당히 놀라게 했다고 발표했습니다.

20세기 후반 대부분의 기간 동안 $H_{0}$ {\ $displaystyle$ H_{ $0}}$ 의 값은 50~90(km/s)/Mpc로 추정되었습니다 $H_{0}$ .

허블상수의 값은 100 정도라고 주장한 제라르 드 보쿨레르와 50 정도라고 주장한 앨런 샌디지 사이에 길고 다소 쓰라린 논쟁의 주제였습니다.^[71] 당사자들 사이에 공유된 독설의 한 예에서, Sandage와 Gustav Andreas Tammann(Sandage의 연구 동료)이 1975년에 그들의 방법의 체계적인 오류를 확인하는 데 있어서의 단점을 공식적으로 인정했을 때, Vaucouleurs는 "이 냉정한 경고가 곧 대부분의 천문학자들과 교과서 집필자들에 의해 잊혀지고 무시된 것은 불행한 일입니다"^[72]라고 대답했습니다. 1996년 존 바콜이 사회를 맡은 시드니 반 덴 버그와 구스타프 탐만 사이의 토론은 이 두 경쟁적인 가치에 대한 이전의 샤플리-커티스 토론과 유사한 방식으로 열렸습니다.

이전에 추정치의 이러한 광범위한 차이는 1990년대 후반 우주의 λCDM 모델이 도입되면서 부분적으로 해결되었습니다. 선야예프-젤도비치 효과를 사용하여 X선 및 마이크로파 파장에서 고적색편이 성단을 λCDM 모델로 관찰한 결과, 우주 마이크로파 배경 복사의 이방성 측정 및 광학 조사 모두 상수에 대해 약 70의 값을 제공했습니다.

21세기 치수

2018년에 발표된 플랑크 미션에서 보다 최근에 측정한 결과 67.66±0.42(km/s)/Mpc의 낮은 값을 나타냈지만, 더욱 최근인 2019년 3월 허블 우주 망원경과 관련된 개선된 절차를 사용하여 74.03±1.42(km/s)/Mpc의 높은 값이 결정되었습니다.^[73] 두 측정값이 4.4 σ 수준에서 일치하지 않으며, 그럴듯한 확률 수준을 넘습니다. 이 불일치에 대한 해결은 활발한 연구가 진행 중인 분야입니다.^[75]

2018년 10월, 과학자들은 중력파 사건(특히 GW170817과 같은 중성자별의 합병과 관련된 사건)의 정보를 사용하여 허블 상수를 결정하는 새로운 세 번째 방법(하나는 적색편이를 기반으로 하고 다른 하나는 우주 거리 사다리에 기반한 이전의 두 가지 방법이 일치하지 않는 결과를 제공)을 제시했습니다.^[76]^[77]

2019년 7월, 천문학자들은 어두운 사이렌으로 알려진 사건인 GW170817의 중성자별 병합이 감지된 후, 중성자별 쌍의 병합을 기반으로 허블 상수를 결정하고 이전 방법의 불일치를 해결하기 위한 새로운 방법이 제안되었다고 보고했습니다.^[78]^[79] 허블상수의 측정값은 73.3+5.3-5
.0(km/s)/Mpc입니다.^[80]

또한 2019년 7월, 천문학자들은 허블 우주 망원경의 데이터를 사용하고 적색 거성 분기(TRGB) 거리 표시기의 끝을 사용하여 계산된 적색 거성까지의 거리를 기반으로 하는 또 다른 새로운 방법을 보고했습니다. 허블상수의 측정값은 69.8+1.9-1
.9(km/s)/Mpc입니다.^[81]^[82]^[83]

2020년 2월 메가마저 우주론 프로젝트는 95%^[84]의 통계적 유의 수준에서 거리 사다리 결과를 확인하고 초기 우주 결과와 다른 독립적인 결과를 발표했습니다. 2020년 7월, 아타카마 우주론 망원경의 우주 배경 복사 측정은 우주가 현재 관측되는 것보다 더 느리게 팽창할 것이라고 예측합니다.^[85]

허블상수 측정
발행일자	허블상수 (km/s)/Mpc	옵저버	인용	비고/방법론
2023-07-13	68.3±1.5	SPT-3G	^[86]	CMB TT/TE/EE 전력 스펙트럼. 플랑크와의 σ 불일치가 1개 미만입니다.
2023-05-11	66.6+4.1 −3.3	P. L. Kelly et al.	^[87]	Supernova Refsdal의 중력 렌즈 이미지의 타이밍 지연. 우주 거리 사다리나 CMB와는 무관합니다.
2022-12-14	67.3+10.0 −9.1	S. Contarini et al.	^[88]	BOSS DR12 데이터 세트(Preprint)를 이용한 우주 공극 통계.^[89]
2022-02-08	73.4+0.99 −1.22	판테온+	^[90]	SNIa 거리 사다리(+SH0ES)
2022-06-17	75.4+3.8 −3.7	T. de Jaeger et al.	^[91]	유형 II 초신성을 표준화 가능한 양초로 사용하여 세페이드 변수에서 측정한 호스트-은하 거리, 적색 거성 가지 끝, 기하학적 거리(NGC 4258)로 허블 상수 13 SNe II를 독립적으로 측정합니다.
2021-12-08	73.04±1.04	SH0ES	^[92]	Cepheids-SNIa 거리 사다리(HST+Gaia EDR3+"Pantheon+"). 플랑크와의 5σ 불일치.
2021-09-17	69.8±1.7	W. 프리드먼	^[93]	적색 거성 분기(TRGB) 거리 표시기 팁(HST+Gaia EDR3)
2020-12-16	72.1±2.0	허블 우주 망원경과 가이아 EDR3	^[94]	적색 거성에 대한 초기 연구와 적색 거성 분기(TRGB) 거리 표시기의 끝을 사용하여 가이아 EDR3의 오메가 센타우루스자리 시차 측정을 결합합니다.
2020-12-15	73.2±1.3	허블 우주 망원경과 가이아 EDR3	^[95]	HST 측광법과 은하 세페이드에 대한 Gaia EDR3 시차를 결합하여 세페이드 광도 보정의 불확실성을 1.0%로 낮춥니다. $H_{0}$ ${\$ 값의 전체 불확실성은 1.8%이며 $H_{0}$ , 세페이드 호스트로 알려진 은하의 Ia형 초신성 샘플이 더 많아지면 1.3%로 감소할 것으로 예상됩니다. 암흑 에너지 상태 방정식 $H_{0}$ SHOES)을 위한 초신성, H $H_{0}$ ${\$ 라는 공동 작업의 계속.
2020-12-04	73.5±5.3	E. J. Baxter, B. D. 셔윈	^[96]	CMB의 중력 렌즈는 사운드 지평선 스케일을 참조하지 않고 $H_{0}$ $H_{0}$ 0 ${\$ 을 추정하는 데 사용되어 플랑크 데이터를 분석할 수 있는 대체 방법을 제공합니다.
2020-11-25	71.8+3.9 −3.3	P. 덴젤 외.	^[97]	8개의 4배 렌즈 은하계가 H0 ${\$ 를 " $H_{0}$ "와 "후기" 우주 추정치와 일치하는 5%의 정밀도로 결정하는 $H_{0}$ 데 사용됩니다. 거리 사다리와 우주 마이크로파 배경에 무관합니다.
2020-11-07	67.4±1.0	T. Sedgwick et al.	^[98]	표준 양초 거리 $z$ 로사용되는 880. $02$ < z ${\$ displaystyle z} < 0. $z$ 05 Type Ia 초신성에서 파생되었습니다. $H_{0}$ $H_{0}$ ${\$ 추정치는 $H_{0}$ 은하 밀도 필드에서 추정한 대로 초신성 환경에서 특이한 속도의 영향에 대해 수정됩니다. 결과는 ω = 0.3, ω = 0.7, 사운드 지평선 149.3 Mpc로 Anderson et al.(2014)에서 가져온 값이라고 가정합니다.
2020-09-29	67.6+4.3 −4.2	S. Mukherjee et al.	^[100]	Zwicky Transient Facility에 의해 발견된 과도 ZTF19abanrh가 GW190521의 광학 대응물이라고 가정할 때 중력파. 거리 사다리와 우주 마이크로파 배경에 무관합니다.
2020-06-18	75.8+5.2 −4.9	T. de Jaeger et al.	^[101]	유형 II 초신성을 표준화 가능한 양초로 사용하여 세페이드 변수 또는 적색 거성 가지 끝에서 측정된 호스트-은하 거리로 허블 상수 7 SNe II를 독립적으로 측정할 수 있습니다.
2020-02-26	73.9±3.0	메가마저 우주론 프로젝트	^[84]	메가마저 호스트 은하까지의 기하학적 거리 측정. 거리 사다리와 우주 마이크로파 배경에 무관합니다.
2019-10-14	74.2+2.7 −3.0	약진	^[102]	렌즈형 퀘이사 DES J0408-5354의 질량 분포 및 시간 지연 모델링.
2019-09-12	76.8±2.6	SHARP/H0LiCOW	^[103]	지상 적응광학과 허블 우주망원경을 이용하여 은하계 렌즈 3개와 그 렌즈를 모델링.
2019-08-20	73.3+1.36 −1.35	K. Dutta et al.	^[104]	이 $H_{0}$ $H_{0}$ $H_{0}$ 은 λCDM 모델 내에서 저적색 이동 우주 데이터를 분석하여 얻은 것입니다. 사용된 데이터 세트는 유형 Ia 초신성, 중입자 음향 진동, 강한 렌즈를 사용한 시간 지연 측정, 우주 크로노미터를 사용한 $H(z)$ $H(z)$ 측정 $H(z)$ 및 대규모 구조 관측의 성장 측정입니다.
2019-08-15	73.5±1.4	M. J. 리드, D. W. 페스케, A. G. 리스	^[105]	초질량 블랙홀을 이용하여 메시에 106까지의 거리를 측정하고, 이는 대마젤란운에서의 식쌍성 측정과 결합된 것입니다.
2019-07-16	69.8±1.9	허블 우주 망원경	^[81]^[82]^[83]	적색 거성까지의 거리는 적색 거성 분기(TRGB) 거리 표시기의 끝을 사용하여 계산됩니다.
2019-07-10	73.3+1.7 −1.8	H0LiCow 협업	^[106]	다중 이미지 퀘이사의 업데이트된 관측 결과, 현재 6개의 퀘이사를 사용하여 우주 거리 사다리와 무관하고 우주 마이크로파 배경 측정과 무관합니다.
2019-07-08	70.3+5.3 −5.0	LIGO의 과학적 협업과 처녀자리의 협업	^[80]	이전 중력파(GW) 및 전자기파(EM) 데이터와 결합된 GW170817의 무선 대응물을 사용합니다.
2019-03-28	68.0+4.2 −4.1	페르미-LAT	^[107]	은하 외 빛으로 인한 감마선 감쇄. 우주 거리 사다리와 우주 마이크로파 배경과는 무관합니다.
2019-03-18	74.03±1.42	허블 우주 망원경	^[74]	LMC(Large Magellanic Cloud)의 세페이드(Cepheids) 정밀 HST 측광법은 LMC까지의 거리의 불확실성을 2.5%에서 1.3%로 줄입니다. 개정판은 CMB 측정 시 장력을 4.4 σ 레벨(가우시안 오차의 경우 P=99.999%)로 증가시켜 불일치를 가능한 확률 수준 이상으로 높입니다. 암흑 에너지 상태 방정식 $H_{0}$ SHOES)을 위한 초신성, H $H_{0}$ ${\$ 라는 공동 작업의 계속.
2019-02-08	67.78+0.91 −0.87	조셉 라이언 외.	^[108]	평평한 λCDM 모델을 가정한 준성각 크기 및 중입자 음향 진동. 대체 모델은 허블 상수에 대해 서로 다른 값(일반적으로 더 낮은 값)을 가져옵니다.
2018-11-06	67.77±1.30	다크 에너지 서베이	^[109]	중입자 음향진동에 기초한 역거리 사다리법을 이용한 초신성 측정.
2018-09-05	72.5+2.1 −2.3	H0LiCow 협업	^[110]	다중 이미지 퀘이사의 관측, 우주 거리 사다리와 무관하고 우주 마이크로파 배경 측정과 무관합니다.
2018-07-18	67.66±0.42	플랑크 미션	^[111]	Final Planck 2018 결과.
2018-04-27	73.52±1.62	허블 우주 망원경과 가이아	^[112]^[113]	초기 가이아 시차 측정과 함께 은하 세페이드의 추가 HST 측광법. 수정된 값은 3.8 σ 수준의 CMB 측정으로 장력을 증가시킵니다. SHOES 협업의 지속.
2018-02-22	73.45±1.66	허블 우주 망원경	^[114]^[115]	거리 사다리의 향상된 보정을 위한 은하 세페이드의 시차 측정; 이 값은 3.7 σ 수준의 CMB 측정과 불일치를 나타냅니다. 가이아 카탈로그의 최종 출시로 불확실성이 1% 이하로 줄어들 것으로 예상됩니다. SHOES 콜라보.
2017-10-16	70.0+12.0 −8.0	LIGO의 과학적 협업과 처녀자리의 협업	^[116]	일반적인 "표준 양초" 기술과 무관한 표준 사이렌 측정; 이진 중성자별(BNS) 합병 GW170817의 중력파 분석은 우주 규모까지의 광도 거리를 직접 추정했습니다. 향후 10년 동안 50개의 유사한 탐지가 있을 것으로 예상하면 다른 방법론의 긴장을 조정할 수 있습니다.^[117] 중성자별-블랙홀 병합(NSBH)의 탐지 및 분석은 BNS가 허용할 수 있는 것보다 더 큰 정밀도를 제공할 수 있습니다.^[118]
2016-11-22	71.9+2.4 −3.0	허블 우주 망원경	^[119]	강력한 중력 렌즈로 생성된 원거리 가변 소스의 여러 이미지 간의 시간 지연을 사용합니다. $H_{0}$ $H_{0}$ ${\$ COSMOGRAIL's Wellspring (H0LiCOW)의 렌즈 $H_{0}$ .
2016-08-04	76.2+3.4 −2.7	코스믹플로우-3	^[120]	적색편이를 툴리-피셔, 세페이드 변광성, Ia형 초신성을 포함한 다른 거리 방법과 비교. 데이터의 제한적인 추정치는 75±2의 더 정확한 값을 의미합니다.
2016-07-13	67.6+0.7 −0.6	SDSS-III 중입자 진동 분광측량(BOSS)	^[121]	중입자 음향 진동. 확장 설문조사(eBOSS)는 2014년에 시작되어 2020년까지 진행될 예정입니다. 확장된 조사는 빅뱅 이후 30억 년에서 80억 년 사이에 중력의 감속 효과에서 벗어나 우주가 전환되고 있던 시기를 탐색하기 위해 고안되었습니다.^[122]
2016-05-17	73.24±1.74	허블 우주 망원경	^[123]	Ia형 초신성, 앞으로 있을 가이아 측정 및 기타 개선 사항으로 불확실성이 2배 이상 감소할 것으로 예상됩니다. SHOES 콜라보.
2015-02	67.74±0.46	플랑크 미션	^[124]^[125]	플랑크의 전체 임무에 대한 분석 결과는 2014년 12월 1일 이탈리아 페라라에서 열린 컨퍼런스에서 공개되었습니다. 2015년 2월에 임무 결과를 자세히 설명하는 논문 전체가 발표되었습니다.
2013-10-01	74.4±3.0	코스믹플로우-2	^[126]	적색편이를 툴리-피셔, 세페이드 변광성, Ia형 초신성을 포함한 다른 거리 방법과 비교.
2013-03-21	67.80±0.77	플랑크 미션	^[53]^[127]^[128]^[129]^[130]	ESA Planck Surveyor는 2009년 5월에 시작되었습니다. WMAP보다 작은 규모로 CMB를 측정하기 위해 HEMT 방사계와 볼로미터 기술을 사용한 이전 조사보다 4년에 걸쳐 훨씬 더 상세한 우주 마이크로파 방사선 조사를 수행했습니다. 2013년 3월 21일, 플랑크 우주 탐사선의 배후에 있는 유럽 주도의 연구팀은 새로운 CMB 하늘 지도와 허블 상수의 결정을 포함한 우주 탐사선의 데이터를 공개했습니다.
2012-12-20	69.32±0.80	WMAP(9년), 다른 측정과 결합	^[131]
2010	70.4+1.3 −1.4	WMAP(7년), 다른 측정값과 결합	^[132]	이러한 값은 WMAP와 다른 우주 데이터의 조합을 가장 간단한 버전의 λCDM 모델에 맞추는 것에서 비롯됩니다. 데이터가 보다 일반적인 버전에 적합한 경우 H는₀ 더 작고 불확실한 경향이 있습니다. 일반적으로 약 67±4(km/s)/Mpc이지만 일부 모델에서는 63(km/s)/Mpc 근처의 값을 허용합니다.^[133]
2010	71.0±2.5	WMAP만(7년).	^[132]
2009-02	70.5±1.3	WMAP(5년), 다른 측정과 결합	^[134]
2009-02	71.9+2.6 −2.7	WMAP만(5년)	^[134]
2007	70.4+1.5 −1.6	WMAP(3년), 다른 측정과 결합	^[135]
2006-08	76.9+10.7 −8.7	찬드라 엑스선 천문대	^[136]	태양예프-젤도비치 효과와 은하단의 찬드라 X선 관측을 결합했습니다. Planck Collaboration 2013의 표의 불확실성 조정.^[137]
2003	72±5	WMAP(1년차)만	.^[138]
2001-05	72±8	허블 우주망원경 키 프로젝트	^[26]	이 프로젝트는 유사한 정확도를 가진 많은 은하단의 선야예프-젤도비치 효과 관측을 기반으로 H를₀ 측정하는 것과 일치하는 가장 정확한 광학 측정을 확립했습니다.
1996년 이전에	50 — 90(테스트)		^[71]
1994	67±7	초신성 1a 빛 곡선 모양	^[139]	SN 1a의 광도와 그들의 광 곡선 모양 사이의 관계를 결정합니다. 리스 외. SN 1972E의 빛 곡선과 NGC 5253에 대한 세페이드 거리의 비율을 사용하여 상수를 계산했습니다.
1970년대 중반	100±10	제라르 드 보쿨레르스	^[72]	드 보쿨레르스는 그의 100 ± 10을 도출하기 위해 5배 더 많은 1차 지표, 10배 더 많은 보정 방법, 2배 더 많은 2차 지표, 3배 더 많은 은하 데이터 포인트를 사용했기 때문에 샌디지의 허블 상수의 정확도를 향상시켰다고 믿었습니다.
1970년대 초	55(에스티)	앨런 샌디지와 구스타프 탐만	^[140]
1958	75(에스티)	앨런 샌디지	^[141]	이것은 H에₀ 대한 최초의 좋은 추정치였지만, 합의가 이루어지기까지는 수십 년이 걸릴 것입니다.
1956	180	후마슨, 메이올, 샌디지	^[140]
1929	500	에드윈 허블, 후커 망원경	^[142]^[140]^[143]
1927	625	조르주 레마 î트레	^[144]	우주의 팽창에 대한 신호로서 첫 번째 측정과 해석.

메모들

^ 예를 들어, 남극 망원경, 아타카마 우주망원경, 플랑크(우주선)는 모두 초기 우주 동안 허블 매개변수의 독립적인 측정을 제공합니다.
^ 제임스 웹 우주 망원경이 지원하는 가장 최근의 데이터는 허블 우주 망원경의 결과이며, 이는 허블의 세페이드 광도 측정의 체계적인 오류가 허블 장력을 유발할 만큼 중요하지 않음을 시사합니다.^[57]
^ 표준 λCDM에서는 암흑 에너지가 후기 우주에서만 작동합니다. 초기 우주에서는 암흑 에너지의 영향이 너무 작아서 영향을 미치지 못합니다.
^ 표준 λCDM에서 암흑 에너지는 일정한 상태 방정식 w = -1을 갖습니다.

참고 항목

우주의 팽창 가속화 – 우주현상
우주론 – 우주의 기원, 진화, 궁극적 운명에 대한 과학적 연구
암흑물질 – 물질의 가상적 형태
물리 상수에서 이름이 사용되는 과학자 목록
일반 상대성 검정 – 과학 실험

참고문헌

^ "IAU members vote to recommend renaming the Hubble law as the Hubble–Lemaître law" (Press release). IAU. 29 October 2018. Retrieved 2018-10-29.
^ ^a ^b ^c Overbye, Dennis (20 February 2017). "Cosmos Controversy: The Universe Is Expanding, but How Fast?". New York Times. Retrieved 21 February 2017.
^ Coles, P., ed. (2001). Routledge Critical Dictionary of the New Cosmology. Routledge. p. 202. ISBN 978-0-203-16457-0.
^ "Hubble Flow". The Swinburne Astronomy Online Encyclopedia of Astronomy. Swinburne University of Technology. Retrieved 2013-05-14.
^ van den Bergh, S. (2011). "The Curious Case of Lemaitre's Equation No. 24". Journal of the Royal Astronomical Society of Canada. 105 (4): 151. arXiv:1106.1195. Bibcode:2011JRASC.105..151V.
^ Nussbaumer, H.; Bieri, L. (2011). "Who discovered the expanding universe?". The Observatory. 131 (6): 394–398. arXiv:1107.2281. Bibcode:2011Obs...131..394N.
^ Way, M.J. (2013). "Dismantling Hubble's Legacy?". ASP Conference Proceedings. 471: 97–132. arXiv:1301.7294. Bibcode:2013ASPC..471...97W.
^ Friedman, A. (December 1922). "Über die Krümmung des Raumes". Zeitschrift für Physik (in German). 10 (1): 377–386. Bibcode:1922ZPhy...10..377F. doi:10.1007/BF01332580. S2CID 125190902.. (English translation in Friedman, A. (December 1999). "On the Curvature of Space". General Relativity and Gravitation. 31 (12): 1991–2000. Bibcode:1999GReGr..31.1991F. doi:10.1023/A:1026751225741. S2CID 122950995.)
^ Lemaître, G. (1927). "Un univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extra-galactiques". Annales de la Société Scientifique de Bruxelles A (in French). 47: 49–59. Bibcode:1927ASSB...47...49L. 영어로 일부 번역됨
^ ^a ^b Livio, M. (2011). "Lost in translation: Mystery of the missing text solved". Nature. 479 (7372): 171–3. Bibcode:2011Natur.479..171L. doi:10.1038/479171a. PMID 22071745. S2CID 203468083.
^ Livio, M.; Riess, A. (2013). "Measuring the Hubble constant". Physics Today. 66 (10): 41. Bibcode:2013PhT....66j..41L. doi:10.1063/PT.3.2148.
^ Hubble, E. (1929). "A relation between distance and radial velocity among extra-galactic nebulae". Proceedings of the National Academy of Sciences. 15 (3): 168–173. Bibcode:1929PNAS...15..168H. doi:10.1073/pnas.15.3.168. PMC 522427. PMID 16577160.
^ Slipher, V.M. (1917). "Radial velocity observations of spiral nebulae". The Observatory. 40: 304–306. Bibcode:1917Obs....40..304S.
^ Longair, M. S. (2006). The Cosmic Century. Cambridge University Press. p. 109. ISBN 978-0-521-47436-8.
^ Nussbaumer, Harry (2013). 'Slipher's redshifts as support for de Sitter's model and the discovery of the dynamic universe' In Origins of the Expanding Universe: 1912–1932. Astronomical Society of the Pacific. pp. 25–38. arXiv:1303.1814.
^ Overbye, Dennis (25 February 2019). "Have Dark Forces Been Messing With the Cosmos? – Axions? Phantom energy? Astrophysicists scramble to patch a hole in the universe, rewriting cosmic history in the process". The New York Times. Retrieved 26 February 2019.
^ O'Raifeartaigh, Cormac (2013). The Contribution of V.M. Slipher to the discovery of the expanding universe in 'Origins of the Expanding Universe'. Astronomical Society of the Pacific. pp. 49–62. arXiv:1212.5499.
^ "Three steps to the Hubble constant". www.spacetelescope.org. Retrieved 26 February 2018.
^ Slipher, V. M. (1913). "The Radial Velocity of the Andromeda Nebula". Lowell Observatory Bulletin. 1 (8): 56–57. Bibcode:1913LowOB...2...56S.
^ Slipher, V. M. (1915). "Spectrographic Observations of Nebulae". Popular Astronomy. 23: 21–24. Bibcode:1915PA.....23...21S.
^ Friedman, A. (1922). "Über die Krümmung des Raumes". Zeitschrift für Physik (in German). 10 (1): 377–386. Bibcode:1922ZPhy...10..377F. doi:10.1007/BF01332580. S2CID 125190902. Translated to English in Friedmann, A. (1999). "On the Curvature of Space". General Relativity and Gravitation. 31 (12): 1991–2000. Bibcode:1999GReGr..31.1991F. doi:10.1023/A:1026751225741. S2CID 122950995.
^ van den Bergh, Sydney (2011). "The Curious Case of Lemaître's Equation No. 24". Journal of the Royal Astronomical Society of Canada. 105 (4): 151. arXiv:1106.1195. Bibcode:2011JRASC.105..151V.
^ Block, David (2012). 'Georges Lemaitre and Stigler's law of eponymy' in Georges Lemaître: Life, Science and Legacy (Holder and Mitton ed.). Springer. pp. 89–96.
^ Sandage, Allan (December 1989). "Edwin Hubble 1889-1953". Journal of the Royal Astronomical Society of Canada. 83 (6): 351–362. Bibcode:1989JRASC..83..351S.
^ ^a ^b Keel, W. C. (2007). The Road to Galaxy Formation (2nd ed.). Springer. pp. 7–8. ISBN 978-3-540-72534-3.
^ ^a ^b Freedman, W. L.; et al. (2001). "Final results from the Hubble Space Telescope Key Project to measure the Hubble constant". The Astrophysical Journal. 553 (1): 47–72. arXiv:astro-ph/0012376. Bibcode:2001ApJ...553...47F. doi:10.1086/320638. S2CID 119097691.
^ Weinberg, S. (2008). Cosmology. Oxford University Press. p. 28. ISBN 978-0-19-852682-7.
^ Kirshner, R. P. (2003). "Hubble's diagram and cosmic expansion". Proceedings of the National Academy of Sciences. 101 (1): 8–13. Bibcode:2003PNAS..101....8K. doi:10.1073/pnas.2536799100. PMC 314128. PMID 14695886.
^ ^a ^b "What is a Cosmological Constant?". Goddard Space Flight Center. Retrieved 2013-10-17.
^ Isaacson, W. (2007). Einstein: His Life and Universe. Simon & Schuster. p. 354. ISBN 978-0-7432-6473-0.
^ "Einstein's Biggest Blunder? Dark Energy May Be Consistent With Cosmological Constant". Science Daily. 28 November 2007. Retrieved 2013-06-02.
^ Davis, T. M.; Lineweaver, C. H. (2001). "Superluminal Recessional Velocities". AIP Conference Proceedings. 555: 348–351. arXiv:astro-ph/0011070. Bibcode:2001AIPC..555..348D. CiteSeerX 10.1.1.254.1810. doi:10.1063/1.1363540. S2CID 118876362.
^ "Is the universe expanding faster than the speed of light?". Ask an Astronomer at Cornell University. Archived from the original on 23 November 2003. Retrieved 5 June 2015.
^ Harrison, E. (1992). "The redshift-distance and velocity-distance laws". The Astrophysical Journal. 403: 28–31. Bibcode:1993ApJ...403...28H. doi:10.1086/172179.
^ Madsen, M. S. (1995). The Dynamic Cosmos. CRC Press. p. 35. ISBN 978-0-412-62300-4.
^ Dekel, A.; Ostriker, J. P. (1999). Formation of Structure in the Universe. Cambridge University Press. p. 164. ISBN 978-0-521-58632-0.
^ Padmanabhan, T. (1993). Structure formation in the universe. Cambridge University Press. p. 58. ISBN 978-0-521-42486-8.
^ Sartori, L. (1996). Understanding Relativity. University of California Press. p. 163, Appendix 5B. ISBN 978-0-520-20029-6.
^ Sartori, L. (1996). Understanding Relativity. University of California Press. pp. 304–305. ISBN 978-0-520-20029-6.
^ Matts Roos, 우주론 입문
^ Scharping, Nathaniel (18 October 2017). "Gravitational Waves Show How Fast The Universe is Expanding". Astronomy. Retrieved 18 October 2017.
^ ^a ^b Chase, S. I.; Baez, J. C. (2004). "Olbers' Paradox". The Original Usenet Physics FAQ. Retrieved 2013-10-17.
^ ^a ^b Asimov, I. (1974). "The Black of Night". Asimov on Astronomy. Doubleday. ISBN 978-0-385-04111-9.
^ Croton, Darren J. (14 October 2013). "Damn You, Little h! (Or, Real-World Applications of the Hubble Constant Using Observed and Simulated Data)". Publications of the Astronomical Society of Australia. 30. arXiv:1308.4150. Bibcode:2013PASA...30...52C. doi:10.1017/pasa.2013.31. S2CID 119257465. Retrieved 8 December 2021.
^ Peebles, P. J. E. (1993). Principles of Physical Cosmology. Princeton University Press.
^ Perlmutter, S. (2003). "Supernovae, Dark Energy, and the Accelerating Universe" (PDF). Physics Today. 56 (4): 53–60. Bibcode:2003PhT....56d..53P. CiteSeerX 10.1.1.77.7990. doi:10.1063/1.1580050. Archived (PDF) from the original on 2022-10-09.
^ Carroll, Sean (2004). Spacetime and Geometry: An Introduction to General Relativity (illustrated ed.). San Francisco: Addison-Wesley. p. 328. ISBN 978-0-8053-8732-2.
^ Heneka, C.; Amendola, L. (2018). "General modified gravity with 21cm intensity mapping: simulations and forecast". Journal of Cosmology and Astroparticle Physics. 2018 (10): 004. arXiv:1805.03629. Bibcode:2018JCAP...10..004H. doi:10.1088/1475-7516/2018/10/004. S2CID 119224326.
^ Tawfik, A.; Harko, T. (2012). "Quark-hadron phase transitions in the viscous early universe". Physical Review D. 85 (8): 084032. arXiv:1108.5697. Bibcode:2012PhRvD..85h4032T. doi:10.1103/PhysRevD.85.084032. S2CID 73716828.
^ Tawfik, A. (2011). "The Hubble parameter in the early universe with viscous QCD matter and finite cosmological constant". Annalen der Physik. 523 (5): 423–434. arXiv:1102.2626. Bibcode:2011AnP...523..423T. doi:10.1002/andp.201100038. S2CID 118500485.
^ Tawfik, A.; Wahba, M.; Mansour, H.; Harko, T. (2011). "Viscous quark-gluon plasma in the early universe". Annalen der Physik. 523 (3): 194–207. arXiv:1001.2814. Bibcode:2011AnP...523..194T. doi:10.1002/andp.201000052. S2CID 119271582.
^ Hawley, John F.; Holcomb, Katherine A. (2005). Foundations of modern cosmology (2nd ed.). Oxford [u.a.]: Oxford University Press. p. 304. ISBN 978-0-19-853096-1.
^ ^a ^b Bucher, P. A. R.; et al. (Planck Collaboration) (2013). "Planck 2013 results. I. Overview of products and scientific Results". Astronomy & Astrophysics. 571: A1. arXiv:1303.5062. Bibcode:2014A&A...571A...1P. doi:10.1051/0004-6361/201321529. S2CID 218716838.
^ Mann, Adam (26 August 2019). "One Number Shows Something Is Fundamentally Wrong with Our Conception of the Universe – This fight has universal implications". Live Science. Retrieved 26 August 2019.
^ ^a ^b ^c ^d ^e ^f di Valentino, Eleonora; et al. (2021). "In the realm of the Hubble tension—a review of solutions". Classical and Quantum Gravity. 38 (15): 153001. arXiv:2103.01183. Bibcode:2021CQGra..38o3001D. doi:10.1088/1361-6382/ac086d. S2CID 232092525.
^ Gresko, Michael (17 December 2021). "The universe is expanding faster than it should be". National Geographic. Archived from the original on December 17, 2021. Retrieved 21 December 2021.
^ Starr, Michelle (14 September 2023). "JWST Just Measured The Expansion Rate of The Universe. Astronomers Are Stumped". ScienceAlert. Archived from the original on 16 September 2023. Retrieved 16 September 2023.
^ Abdalla, Elcio; Abellán, Guillermo Franco; Aboubrahim, Amin (11 Mar 2022), "Cosmology Intertwined: A Review of the Particle Physics, Astrophysics, and Cosmology Associated with the Cosmological Tensions and Anomalies", Journal of High Energy Astrophysics, 34: 49, arXiv:2203.06142v1, Bibcode:2022JHEAp..34...49A, doi:10.1016/j.jheap.2022.04.002, S2CID 247411131
^ Rameez, Mohamed; Sarkar, Subir (15 July 2021). "Is there really a Hubble tension?". Classical and Quantum Gravity. 38 (15): 154005. arXiv:1911.06456. Bibcode:2021CQGra..38o4005R. doi:10.1088/1361-6382/ac0f39. ISSN 0264-9381. S2CID 208075753.
^ Singh, Ritesh (28 October 2021). "Evidence for possible systematic underestimation of uncertainties in extragalactic distances and its cosmological implications". Astrophysics and Space Science. 366 (10): 99. arXiv:2111.07872. Bibcode:2021Ap&SS.366...99S. doi:10.1007/s10509-021-04006-5. ISSN 1572-946X. S2CID 240179422.
^ Haslbauer, M.; Banik, I.; Kroupa, P. (2020-12-21). "The KBC void and Hubble tension contradict LCDM on a Gpc scale – Milgromian dynamics as a possible solution". Monthly Notices of the Royal Astronomical Society. 499 (2): 2845–2883. arXiv:2009.11292. Bibcode:2020MNRAS.499.2845H. doi:10.1093/mnras/staa2348. ISSN 0035-8711.
^ Poulin, Vivian; Smith, Tristan L.; Karwal, Tanvi; Kamionkowski, Marc (2019-06-04). "Early Dark Energy can Resolve the Hubble Tension". Physical Review Letters. 122 (22): 221301. arXiv:1811.04083. Bibcode:2019PhRvL.122v1301P. doi:10.1103/PhysRevLett.122.221301. PMID 31283280. S2CID 119233243.
^ Zhao, Gong-Bo; Raveri, Marco; Pogosian, Levon; Wang, Yuting; Crittenden, Robert G.; Handley, Will J.; Percival, Will J.; Beutler, Florian; Brinkmann, Jonathan; Chuang, Chia-Hsun; Cuesta, Antonio J.; Eisenstein, Daniel J.; Kitaura, Francisco-Shu; Koyama, Kazuya; l'Huillier, Benjamin; Nichol, Robert C.; Pieri, Matthew M.; Rodriguez-Torres, Sergio; Ross, Ashley J.; Rossi, Graziano; Sánchez, Ariel G.; Shafieloo, Arman; Tinker, Jeremy L.; Tojeiro, Rita; Vazquez, Jose A.; Zhang, Hanyu (2017). "Dynamical dark energy in light of the latest observations". Nature Astronomy. 1 (9): 627–632. arXiv:1701.08165. doi:10.1038/s41550-017-0216-z. S2CID 256705070.
^ Berezhiani, Zurab; Dolgov, A. D.; Tkachev, I. I. (2015). "Reconciling Planck results with low redshift astronomical measurements". Physical Review D. 92 (6): 061303. arXiv:1505.03644. doi:10.1103/PhysRevD.92.061303. S2CID 118169478.
^ Laila Linke (17 May 2021). "Solving the Hubble tension might require more than changing the early Universe". Astrobites.
^ Vagnozzi, Sunny (2023-08-30). "Seven Hints That Early-Time New Physics Alone Is Not Sufficient to Solve the Hubble Tension". Universe. 9 (9): 393. arXiv:2308.16628. Bibcode:2023Univ....9..393V. doi:10.3390/universe9090393.
^ Ryan E. Keeley and Arman Shafieloo (August 2023). "Ruling Out New Physics at Low Redshift as a Solution to the H₀ Tension". Physical Review Letters. 131 (11): 111002. arXiv:2206.08440. doi:10.1103/PhysRevLett.131.111002. PMID 37774270. S2CID 249848075.
^ Baade, W. (1944) 메시에 32의 해상도, NGC 205, 안드로메다 성운의 중심 영역. ApJ 100 137–146
^ Baade, W. (1956) 세페이드족의 주기-광도 관계. PASP 68 5–16
^ Allen, Nick. "Section 2: The Great Debate and the Great Mistake: Shapley, Hubble, Baade". The Cepheid Distance Scale: A History. Archived from the original on 10 December 2007. Retrieved 19 November 2011.
^ ^a ^b Overbye, D. (1999). "Prologue". Lonely Hearts of the Cosmos (2nd ed.). HarperCollins. p. 1ff. ISBN 978-0-316-64896-7.
^ ^a ^b de Vaucouleurs, G. (1982). The cosmic distance scale and the Hubble constant. Mount Stromlo and Siding Spring Observatories, Australian National University.
^ Ananthaswamy, Anil (22 March 2019). "Best-Yet Measurements Deepen Cosmological Crisis". Scientific American. Retrieved 23 March 2019.
^ ^a ^b Riess, Adam G.; Casertano, Stefano; Yuan, Wenlong; Macri, Lucas M.; Scolnic, Dan (18 March 2019). "Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics Beyond LambdaCDM". The Astrophysical Journal. 876 (1): 85. arXiv:1903.07603. Bibcode:2019ApJ...876...85R. doi:10.3847/1538-4357/ab1422. S2CID 85528549.
^ Millea, Marius; Knox, Lloyd (2019-08-10). "The Hubble Hunter's Guide". arXiv:1908.03663v1 [astro-ph.CO].
^ Lerner, Louise (22 October 2018). "Gravitational waves could soon provide measure of universe's expansion". Phys.org. Retrieved 22 October 2018.
^ Chen, Hsin-Yu; Fishbach, Maya; Holz, Daniel E. (17 October 2018). "A two per cent Hubble constant measurement from standard sirens within five years". Nature. 562 (7728): 545–547. arXiv:1712.06531. Bibcode:2018Natur.562..545C. doi:10.1038/s41586-018-0606-0. PMID 30333628. S2CID 52987203.
^ National Radio Astronomy Observatory (8 July 2019). "New method may resolve difficulty in measuring universe's expansion – Neutron star mergers can provide new 'cosmic ruler'". EurekAlert!. Retrieved 8 July 2019.
^ Finley, Dave (8 July 2019). "New Method May Resolve Difficulty in Measuring Universe's Expansion". National Radio Astronomy Observatory. Retrieved 8 July 2019.
^ ^a ^b Hotokezaka, K.; et al. (8 July 2019). "A Hubble constant measurement from superluminal motion of the jet in GW170817". Nature Astronomy. 3 (10): 940–944. arXiv:1806.10596. Bibcode:2019NatAs...3..940H. doi:10.1038/s41550-019-0820-1. S2CID 119547153.
^ ^a ^b Carnegie Institution of Science (16 July 2019). "New measurement of universe's expansion rate is 'stuck in the middle' – Red giant stars observed by Hubble Space Telescope used to make an entirely new measurement of how fast the universe is expanding". EurekAlert!. Retrieved 16 July 2019.
^ ^a ^b Sokol, Joshua (19 July 2019). "Debate intensifies over speed of expanding universe". Science. doi:10.1126/science.aay8123. S2CID 200021863. Retrieved 20 July 2019.
^ ^a ^b Freedman, Wendy L.; Madore, Barry F.; Hatt, Dylan; Hoyt, Taylor J.; Jang, In-Sung; Beaton, Rachael L.; et al. (2019). "The Carnegie-Chicago Hubble Program. VIII. An Independent Determination of the Hubble Constant Based on the Tip of the Red Giant Branch". The Astrophysical Journal. 882 (1): 34. arXiv:1907.05922. Bibcode:2019ApJ...882...34F. doi:10.3847/1538-4357/ab2f73. S2CID 196623652.
^ ^a ^b Pesce, D. W.; Braatz, J. A.; Reid, M. J.; Riess, A. G.; et al. (26 February 2020). "The Megamaser Cosmology Project. XIII. Combined Hubble Constant Constraints". The Astrophysical Journal. 891 (1): L1. arXiv:2001.09213. Bibcode:2020ApJ...891L...1P. doi:10.3847/2041-8213/ab75f0. S2CID 210920444.
^ Castelvecchi, Davide (2020-07-15). "Mystery over Universe's expansion deepens with fresh data". Nature. 583 (7817): 500–501. Bibcode:2020Natur.583..500C. doi:10.1038/d41586-020-02126-6. PMID 32669728. S2CID 220583383.
^ SPT-3G Collaboration; Balkenhol, L.; Dutcher, D.; Spurio Mancini, A.; Doussot, A.; Benabed, K.; Galli, S.; Ade, P. A. R.; Anderson, A. J.; Ansarinejad, B.; Archipley, M.; Bender, A. N.; Benson, B. A.; Bianchini, F.; Bleem, L. E. (2023-07-13). "Measurement of the CMB temperature power spectrum and constraints on cosmology from the SPT-3G 2018 $TT$, $TE$, and $EE$ dataset". Physical Review D. 108 (2): 023510. arXiv:2212.05642v3. doi:10.1103/PhysRevD.108.023510. S2CID 259887685.{{cite journal}}: CS1 main: 숫자 이름: 저자 목록 (링크)
^ Kelly, P. L.; Rodney, S.; Treu, T.; Oguri, M.; Chen, W.; Zitri, A.; et al. (2023-05-11). "Constraints on the Hubble constant from Supernova Refsdal's reappearance". Science. 380 (6649): eabh1322. arXiv:2305.06367. Bibcode:2023Sci...380.1322K. doi:10.1126/science.abh1322. PMID 37167351. S2CID 258615332.
^ Contarini, Sofia; Pisani, Alice; Hamaus, Nico; Marulli, Federico; Moscardini, Lauro; Baldi, Marco (2022). "Voids fill us in on rising cosmology tensions". arXiv:2212.07438 [astro-ph.CO].
^ Chiou, Lyndie (2023-07-25). "How (Nearly) Nothing Might Solve Cosmology's Biggest Questions". Quanta Magazine. Retrieved 2023-07-31.
^ Brout, Dillon; Scolnic, Dan; Popovic, Brodie; Riess, Adam G.; Carr, Anthony; Zuntz, Joe; Kessler, Rick; Davis, Tamara M.; Hinton, Samuel; Jones, David; Kenworthy, W. D'Arcy; Peterson, Erik R.; Said, Khaled; Taylor, Georgie; Ali, Noor; Armstrong, Patrick; Charvu, Pranav; Dwomoh, Arianna; Meldorf, Cole; Palmese, Antonella; Qu, Helen; Rose, Benjamin M.; Sanchez, Bruno; Stubbs, Christopher W.; Vincenzi, Maria; Wood, Charlotte M.; Brown, Peter J.; Chen, Rebecca; Chambers, Ken; Coulter, David A.; Dai, Mi; Dimitriadis, Georgios; Filippenko, Alexi V.; Foley, Ryan J.; Jha, Saurabh W.; Kelsey, Lisa; Kirshner, Robert P.; Möller, Anais; Muir, Jessie; Nadathur, Seshadri; Pan, Yen-Chen; Rest, Armin; Rojas-Bravo, Cesar; Sako, Masao; Siebert, Matthew R.; Smith, Mat; Stahl, Benjamin E.; Wiseman, Phil (2022-02-08). "The Pantheon+ Analysis: Cosmological Constraints". The Astrophysical Journal. 938 (2): 110. arXiv:2202.04077. Bibcode:2022ApJ...938..110B. doi:10.3847/1538-4357/ac8e04. S2CID 246679941.
^ de Jaeger, T.; Galbany, L.; Riess, A. G.; Stahl, Ben E.; et al. (17 June 2022). "A 5 per cent measurement of the Hubble–Lemaître constant from Type II supernovae". MNRAS. 514 (3): 4620–4628. arXiv:2203.08974. doi:10.1093/mnras/stac1661.
^ Riess, Adam G.; Yuan, Wenlong; Macri, Lucas M.; Scolnic, Dan; Brout, Dillon; Casertano, Stefano; Jones, David O.; Murakami, Yukei; Breuval, Louise; Brink, Thomas G.; Filippenko, Alexei V. (2021-12-08). "A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km/s/Mpc Uncertainty from the Hubble Space Telescope and the SH0ES Team". The Astrophysical Journal. 934 (1). arXiv:2112.04510. Bibcode:2022ApJ...934L...7R. doi:10.3847/2041-8213/ac5c5b. S2CID 245005861.
^ Freedman, Wendy L. (2021-09-01). "Measurements of the Hubble Constant: Tensions in Perspective*". The Astrophysical Journal. 919 (1): 16. arXiv:2106.15656. Bibcode:2021ApJ...919...16F. doi:10.3847/1538-4357/ac0e95. ISSN 0004-637X. S2CID 235683396.
^ Soltis, J.; Casertano, S.; Riess, A. G. (2021). "The Parallax of Omega Centauri Measured from Gaia EDR3 and a Direct, Geometric Calibration of the Tip of the Red Giant Branch and the Hubble Constant". The Astrophysical Journal. 908 (1): L5. arXiv:2012.09196. Bibcode:2021ApJ...908L...5S. doi:10.3847/2041-8213/abdbad. S2CID 229297709.
^ Riess, A. G.; Casertano, S.; Yuan, W.; Bowers, J. B.; et al. (2021). "Cosmic Distances Calibrated to 1% Precision with Gaia EDR3 Parallaxes and Hubble Space Telescope Photometry of 75 Milky Way Cepheids Confirm Tension with LambdaCDM". The Astrophysical Journal. 908 (1): L6. arXiv:2012.08534. Bibcode:2021ApJ...908L...6R. doi:10.3847/2041-8213/abdbaf. S2CID 229213131.
^ Baxter, E. J.; Sherwin, B. D. (February 2021). "Determining the Hubble constant without the sound horizon scale: measurements from CMB lensing". Monthly Notices of the Royal Astronomical Society. 501 (2): 1823–1835. arXiv:2007.04007. Bibcode:2021MNRAS.501.1823B. doi:10.1093/mnras/staa3706. S2CID 220404332.
^ Denzel, P.; Coles, J. P.; Saha, P.; Williams, L. L. R. (February 2021). "The Hubble constant from eight time-delay galaxy lenses". Monthly Notices of the Royal Astronomical Society. 501 (1): 784–801. arXiv:2007.14398. Bibcode:2021MNRAS.501..784D. doi:10.1093/mnras/staa3603. S2CID 220845622.
^ Sedgwick, Thomas M; Collins, Chris A; Baldry, Ivan K; James, Philip A (2020-11-07). "The effects of peculiar velocities in SN Ia environments on the local H0 measurement". Monthly Notices of the Royal Astronomical Society. 500 (3): 3728–3742. arXiv:1911.03155. doi:10.1093/mnras/staa3456. ISSN 0035-8711.
^ Anderson, Lauren; Aubourg, Éric; Bailey, Stephen; Beutler, Florian; Bhardwaj, Vaishali; Blanton, Michael; Bolton, Adam S.; Brinkmann, J.; Brownstein, Joel R.; Burden, Angela; Chuang, Chia-Hsun (2014-04-21). "The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: baryon acoustic oscillations in the Data Releases 10 and 11 Galaxy samples". Monthly Notices of the Royal Astronomical Society. 441 (1): 24–62. doi:10.1093/mnras/stu523. hdl:2445/101758. ISSN 1365-2966.
^ Mukherjee, S.; Ghosh, A.; Graham, M. J.; Karathanasis, C.; et al. (29 September 2020). "First measurement of the Hubble parameter from bright binary black hole GW190521". arXiv:2009.14199 [astro-ph.CO].
^ de Jaeger, T.; Stahl, B.; Zheng, W.; Filippenko, A.V.; et al. (18 June 2020). "A measurement of the Hubble constant from Type II supernovae". MNRAS. 496 (3): 3402–3411. arXiv:2006.03412. doi:10.1093/mnras/staa1801.
^ Shajib, A. J.; Birrer, S.; Treu, T.; Agnello, A.; et al. (14 October 2019). "STRIDES: A 3.9 per cent measurement of the Hubble constant from the strongly lensed system DES J0408-5354". Monthly Notices of the Royal Astronomical Society. arXiv:1910.06306. doi:10.1093/mnras/staa828. S2CID 204509190.
^ Chen, G.C.-F.; Fassnacht, C.D.; Suyu, S.H.; Rusu, C.E.; et al. (12 September 2019). "A SHARP view of H0LiCOW: H0 from three time-delay gravitational lens systems with adaptive optics imaging". Monthly Notices of the Royal Astronomical Society. 490 (2): 1743–1773. arXiv:1907.02533. Bibcode:2019MNRAS.490.1743C. doi:10.1093/mnras/stz2547. S2CID 195820422.
^ Dutta, Koushik; Roy, Anirban; Ruchika, Ruchika; Sen, Anjan A.; Sheikh-Jabbari, M. M. (20 August 2019). "Cosmology With Low-Redshift Observations: No Signal For New Physics". Phys. Rev. D. 100 (10): 103501. arXiv:1908.07267. Bibcode:2019PhRvD.100j3501D. doi:10.1103/PhysRevD.100.103501. S2CID 201107151.
^ Reid, M. J.; Pesce, D. W.; Riess, A. G. (15 August 2019). "An Improved Distance to NGC 4258 and its Implications for the Hubble Constant". The Astrophysical Journal. 886 (2): L27. arXiv:1908.05625. Bibcode:2019ApJ...886L..27R. doi:10.3847/2041-8213/ab552d. S2CID 199668809.
^ Kenneth C. Wong (2020). "H0LiCOW XIII. A 2.4% measurement of H₀ from lensed quasars: 5.3σ tension between early and late-Universe probes". Monthly Notices of the Royal Astronomical Society. arXiv:1907.04869. doi:10.1093/mnras/stz3094. S2CID 195886279.
^ Domínguez, Alberto; et al. (28 March 2019). "A new measurement of the Hubble constant and matter content of the Universe using extragalactic background light γ-ray attenuation". The Astrophysical Journal. 885 (2): 137. arXiv:1903.12097. Bibcode:2019ApJ...885..137D. doi:10.3847/1538-4357/ab4a0e. S2CID 85543845.
^ Ryan, Joseph; Chen, Yun; Ratra, Bharat (8 February 2019). "Baryon acoustic oscillation, Hubble parameter, and angular size measurement constraints on the Hubble constant, dark energy dynamics, and spatial curvature". Monthly Notices of the Royal Astronomical Society. 488 (3): 3844–3856. arXiv:1902.03196. Bibcode:2019MNRAS.488.3844R. doi:10.1093/mnras/stz1966. S2CID 119226802.
^ Macaulay, E; et al. (DES collaboration) (2018). "First Cosmological Results using Type Ia Supernovae from the Dark Energy Survey: Measurement of the Hubble Constant". Monthly Notices of the Royal Astronomical Society. 486 (2): 2184–2196. arXiv:1811.02376. doi:10.1093/mnras/stz978. S2CID 119310644.
^ Birrer, S.; Treu, T.; Rusu, C. E.; Bonvin, V.; Fassnacht, C. D.; Chan, J. H. H.; et al. (2018). "H0LiCOW – IX. Cosmographic analysis of the doubly imaged quasar SDSS 1206+4332 and a new measurement of the Hubble constant". Monthly Notices of the Royal Astronomical Society. 484 (4): 4726–4753. arXiv:1809.01274. Bibcode:2019MNRAS.484.4726B. doi:10.1093/mnras/stz200. S2CID 119053798.
^ Planck Collaboration; Aghanim, N.; et al. (2018). "Planck 2018 results. VI. Cosmological parameters". arXiv:1807.06209. Bibcode:2018arXiv180706209P.
^ Riess, Adam G.; Casertano, Stefano; Yuan, Wenlong; Macri, Lucas; et al. (2018). "Milky Way Cepheid Standards for Measuring Cosmic Distances and Application to Gaia DR2: Implications for the Hubble Constant". The Astrophysical Journal. 861 (2): 126. arXiv:1804.10655. Bibcode:2018ApJ...861..126R. doi:10.3847/1538-4357/aac82e. ISSN 0004-637X. S2CID 55643027.
^ Devlin, Hannah (10 May 2018). "The answer to life, the universe and everything might be 73. Or 67". the Guardian. Retrieved 13 May 2018.
^ Riess, Adam G.; Casertano, Stefano; Yuan, Wenlong; Macri, Lucas; et al. (22 February 2018). "New parallaxes of galactic Cepheids from spatially scanning the Hubble Space Telescope: Implications for the Hubble constant" (PDF). The Astrophysical Journal. 855 (2): 136. arXiv:1801.01120. Bibcode:2018ApJ...855..136R. doi:10.3847/1538-4357/aaadb7. S2CID 67808349. Archived (PDF) from the original on 2022-10-09. Retrieved 23 February 2018.
^ Weaver, Donna; Villard, Ray; Hille, Karl (22 February 2018). "Improved Hubble Yardstick Gives Fresh Evidence for New Physics in the Universe". NASA. Retrieved 24 February 2018.
^ The LIGO Scientific Collaboration and The Virgo Collaboration; The 1M2H Collaboration; The Dark Energy Camera GW-EM Collaboration and the DES Collaboration; The DLT40 Collaboration; et al. (2017-10-16). "A gravitational-wave standard siren measurement of the Hubble constant" (PDF). Nature. 551 (7678): 85–88. arXiv:1710.05835. Bibcode:2017Natur.551...85A. doi:10.1038/nature24471. ISSN 1476-4687. PMID 29094696. S2CID 205261622. Archived (PDF) from the original on 2022-10-09.{{cite journal}}: CS1 main: 숫자 이름: 저자 목록 (링크)
^ Feeney, Stephen M; Peiris, Hiranya V; Williamson, Andrew R; Nissanke, Samaya M; et al. (2019). "Prospects for resolving the Hubble constant tension with standard sirens". Physical Review Letters. 122 (6): 061105. arXiv:1802.03404. Bibcode:2019PhRvL.122f1105F. doi:10.1103/PhysRevLett.122.061105. hdl:2066/201510. PMID 30822066. S2CID 73493934.
^ Vitale, Salvatore; Chen, Hsin-Yu (12 July 2018). "Measuring the Hubble Constant with Neutron Star Black Hole Mergers". Physical Review Letters. 121 (2): 021303. arXiv:1804.07337. Bibcode:2018PhRvL.121b1303V. doi:10.1103/PhysRevLett.121.021303. hdl:1721.1/117110. PMID 30085719. S2CID 51940146.
^ Bonvin, Vivien; Courbin, Frédéric; Suyu, Sherry H.; et al. (2016-11-22). "H0LiCOW – V. New COSMOGRAIL time delays of HE 0435−1223: H₀ to 3.8 per cent precision from strong lensing in a flat ΛCDM model". MNRAS. 465 (4): 4914–4930. arXiv:1607.01790. Bibcode:2017MNRAS.465.4914B. doi:10.1093/mnras/stw3006. S2CID 109934944.
^ Tully, R. Brent; Courtois, Hélène M.; Sorce, Jenny G. (3 August 2016). "COSMICFLOWS-3". The Astronomical Journal. 152 (2): 50. arXiv:1605.01765. Bibcode:2016AJ....152...50T. doi:10.3847/0004-6256/152/2/50. S2CID 250737862.
^ Grieb, Jan N.; Sánchez, Ariel G.; Salazar-Albornoz, Salvador (2016-07-13). "The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological implications of the Fourier space wedges of the final sample". Monthly Notices of the Royal Astronomical Society. 467 (2): stw3384. arXiv:1607.03143. Bibcode:2017MNRAS.467.2085G. doi:10.1093/mnras/stw3384. S2CID 55888085.
^ "The Extended Baryon Oscillation Spectroscopic Survey (eBOSS)". SDSS. Retrieved 13 May 2018.
^ Riess, Adam G.; Macri, Lucas M.; Hoffmann, Samantha L.; Scolnic, Dan; et al. (2016-04-05). "A 2.4% Determination of the Local Value of the Hubble Constant". The Astrophysical Journal. 826 (1): 56. arXiv:1604.01424. Bibcode:2016ApJ...826...56R. doi:10.3847/0004-637X/826/1/56. S2CID 118630031.
^ "Planck Publications: Planck 2015 Results". European Space Agency. February 2015. Retrieved 9 February 2015.
^ Cowen, Ron; Castelvecchi, Davide (2 December 2014). "European probe shoots down dark-matter claims". Nature. doi:10.1038/nature.2014.16462. Retrieved 6 December 2014.
^ Tully, R. Brent; Courtois, Helene M.; Dolphin, Andrew E.; Fisher, J. Richard; et al. (5 September 2013). "Cosmicflows-2: The Data". The Astronomical Journal. 146 (4): 86. arXiv:1307.7213. Bibcode:2013AJ....146...86T. doi:10.1088/0004-6256/146/4/86. ISSN 0004-6256. S2CID 118494842.
^ "Planck reveals an almost perfect universe". ESA. 21 March 2013. Retrieved 2013-03-21.
^ "Planck Mission Brings Universe Into Sharp Focus". JPL. 21 March 2013. Retrieved 2013-03-21.
^ Overbye, D. (21 March 2013). "An infant universe, born before we knew". New York Times. Retrieved 2013-03-21.
^ Boyle, A. (21 March 2013). "Planck probe's cosmic 'baby picture' revises universe's vital statistics". NBC News. Archived from the original on 2013-03-23. Retrieved 2013-03-21.
^ Bennett, C. L.; et al. (2013). "Nine-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Final maps and results". The Astrophysical Journal Supplement Series. 208 (2): 20. arXiv:1212.5225. Bibcode:2013ApJS..208...20B. doi:10.1088/0067-0049/208/2/20. S2CID 119271232.
^ ^a ^b Jarosik, N.; et al. (2011). "Seven-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Sky maps, systematic errors, and basic results". The Astrophysical Journal Supplement Series. 192 (2): 14. arXiv:1001.4744. Bibcode:2011ApJS..192...14J. doi:10.1088/0067-0049/192/2/14. S2CID 46171526.
^ 다양한 모델을 WMAP 및 기타 데이터의 여러 조합에 맞게 조정하여 얻은₀ H 및 기타 우주론적 매개변수에 대한 결과는 NASA의 LAMDA 웹사이트인 Archive the Wayback Machine 2014-07-09에서 확인할 수 있습니다.
^ ^a ^b Hinshaw, G.; et al. (WMAP Collaboration) (2009). "Five-year Wilkinson Microwave Anisotropy Probe observations: Data processing, sky maps, and basic results". The Astrophysical Journal Supplement. 180 (2): 225–245. arXiv:0803.0732. Bibcode:2009ApJS..180..225H. doi:10.1088/0067-0049/180/2/225. S2CID 3629998.
^ Spergel, D. N.; et al. (WMAP Collaboration) (2007). "Three-year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Implications for cosmology". The Astrophysical Journal Supplement Series. 170 (2): 377–408. arXiv:astro-ph/0603449. Bibcode:2007ApJS..170..377S. doi:10.1086/513700. S2CID 1386346.
^ Bonamente, M.; Joy, M. K.; Laroque, S. J.; Carlstrom, J. E.; et al. (2006). "Determination of the cosmic distance scale from Sunyaev–Zel'dovich effect and Chandra X‐ray measurements of high‐redshift galaxy clusters". The Astrophysical Journal. 647 (1): 25. arXiv:astro-ph/0512349. Bibcode:2006ApJ...647...25B. doi:10.1086/505291. S2CID 15723115.
^ Planck Collaboration (2013). "Planck 2013 results. XVI. Cosmological parameters". Astronomy & Astrophysics. 571: A16. arXiv:1303.5076. Bibcode:2014A&A...571A..16P. doi:10.1051/0004-6361/201321591. S2CID 118349591.
^ Spergel, D.N. (September 2003). "First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters". The Astrophysical Journal Supplement Series. 148 (1): 175–194. arXiv:astro-ph/0302209. Bibcode:2003ApJS..148..175S. doi:10.1086/377226. S2CID 10794058.
^ Riess, Adam G. (January 1995). "Using SN Ia Light Curve Shapes to Measure The Hubble Constant". The Astrophysical Journal. 438 (L17). arXiv:astro-ph/9410054. doi:10.1086/187704. S2CID 118938423.
^ ^a ^b ^c John P. Huchra (2008). "The Hubble Constant". Harvard Center for Astrophysics.
^ Sandage, A. R. (1958). "Current problems in the extragalactic distance scale". The Astrophysical Journal. 127 (3): 513–526. Bibcode:1958ApJ...127..513S. doi:10.1086/146483.
^ 에드윈 허블, 은하 외 성운 사이의 거리와 반지름 속도의 관계, 미국 국립과학원 회보, vol. 15, No. 3, pp. 168-173, 1929년 3월
^ "Hubble's Constant". Skywise Unlimited – Western Washington University.
^ Lemaître, Georges (1927). "Un Univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extra-galactiques". Annales de la Société Scientifique de Bruxelles (in French). A47: 49–59. Bibcode:1927ASSB...47...49L.

서지학

Hubble, E. P. (1937). The Observational Approach to Cosmology. Clarendon Press. LCCN 38011865.
Kutner, M. (2003). Astronomy: A Physical Perspective. Cambridge University Press. ISBN 978-0-521-52927-3.
Liddle, A. R. (2003). An Introduction to Modern Cosmology (2nd ed.). John Wiley & Sons. ISBN 978-0-470-84835-7.

외부 링크

나사의 WMAP 빅뱅 팽창: 허블 상수
허블 키 프로젝트
허블 다이어그램 프로젝트
서로 다른 허블상수들과 합의 (Forbes; 2019년 5월 3일)
Merrifield, Michael (2009). "Hubble Constant". Sixty Symbols. Brady Haran for the University of Nottingham.

[57] 예를 들어, 남극 망원경, 아타카마 우주망원경, 플랑크(우주선)는 모두 초기 우주 동안 허블 매개변수의 독립적인 측정을 제공합니다.

[59] 제임스 웹 우주 망원경이 지원하는 가장 최근의 데이터는 허블 우주 망원경의 결과이며, 이는 허블의 세페이드 광도 측정의 체계적인 오류가 허블 장력을 유발할 만큼 중요하지 않음을 시사합니다.^[57]

[64] 표준 λCDM에서는 암흑 에너지가 후기 우주에서만 작동합니다. 초기 우주에서는 암흑 에너지의 영향이 너무 작아서 영향을 미치지 못합니다.

[66] 표준 λCDM에서 암흑 에너지는 일정한 상태 방정식 w = -1을 갖습니다.

[1] "IAU members vote to recommend renaming the Hubble law as the Hubble–Lemaître law" (Press release). IAU. 29 October 2018. Retrieved 2018-10-29.

[NYT-20170220-2] Overbye, Dennis (20 February 2017). "Cosmos Controversy: The Universe Is Expanding, but How Fast?". New York Times. Retrieved 21 February 2017.

[Coles-3] Coles, P., ed. (2001). Routledge Critical Dictionary of the New Cosmology. Routledge. p. 202. ISBN 978-0-203-16457-0.

[4] "Hubble Flow". The Swinburne Astronomy Online Encyclopedia of Astronomy. Swinburne University of Technology. Retrieved 2013-05-14.

[5] van den Bergh, S. (2011). "The Curious Case of Lemaitre's Equation No. 24". Journal of the Royal Astronomical Society of Canada. 105 (4): 151. arXiv:1106.1195. Bibcode:2011JRASC.105..151V.

[6] Nussbaumer, H.; Bieri, L. (2011). "Who discovered the expanding universe?". The Observatory. 131 (6): 394–398. arXiv:1107.2281. Bibcode:2011Obs...131..394N.

[7] Way, M.J. (2013). "Dismantling Hubble's Legacy?". ASP Conference Proceedings. 471: 97–132. arXiv:1301.7294. Bibcode:2013ASPC..471...97W.

[8] Friedman, A. (December 1922). "Über die Krümmung des Raumes". Zeitschrift für Physik (in German). 10 (1): 377–386. Bibcode:1922ZPhy...10..377F. doi:10.1007/BF01332580. S2CID 125190902.. (English translation in Friedman, A. (December 1999). "On the Curvature of Space". General Relativity and Gravitation. 31 (12): 1991–2000. Bibcode:1999GReGr..31.1991F. doi:10.1023/A:1026751225741. S2CID 122950995.)

[9] Lemaître, G. (1927). "Un univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extra-galactiques". Annales de la Société Scientifique de Bruxelles A (in French). 47: 49–59. Bibcode:1927ASSB...47...49L. 영어로 일부 번역됨

[Livio-10] Livio, M. (2011). "Lost in translation: Mystery of the missing text solved". Nature. 479 (7372): 171–3. Bibcode:2011Natur.479..171L. doi:10.1038/479171a. PMID 22071745. S2CID 203468083.

[11] Livio, M.; Riess, A. (2013). "Measuring the Hubble constant". Physics Today. 66 (10): 41. Bibcode:2013PhT....66j..41L. doi:10.1063/PT.3.2148.

[12] Hubble, E. (1929). "A relation between distance and radial velocity among extra-galactic nebulae". Proceedings of the National Academy of Sciences. 15 (3): 168–173. Bibcode:1929PNAS...15..168H. doi:10.1073/pnas.15.3.168. PMC 522427. PMID 16577160.

[13] Slipher, V.M. (1917). "Radial velocity observations of spiral nebulae". The Observatory. 40: 304–306. Bibcode:1917Obs....40..304S.

[MS_Longair2-14] Longair, M. S. (2006). The Cosmic Century. Cambridge University Press. p. 109. ISBN 978-0-521-47436-8.

[15] Nussbaumer, Harry (2013). 'Slipher's redshifts as support for de Sitter's model and the discovery of the dynamic universe' In Origins of the Expanding Universe: 1912–1932. Astronomical Society of the Pacific. pp. 25–38. arXiv:1303.1814.

[NYT-20190225-16] Overbye, Dennis (25 February 2019). "Have Dark Forces Been Messing With the Cosmos? – Axions? Phantom energy? Astrophysicists scramble to patch a hole in the universe, rewriting cosmic history in the process". The New York Times. Retrieved 26 February 2019.

[17] O'Raifeartaigh, Cormac (2013). The Contribution of V.M. Slipher to the discovery of the expanding universe in 'Origins of the Expanding Universe'. Astronomical Society of the Pacific. pp. 49–62. arXiv:1212.5499.

[18] "Three steps to the Hubble constant". www.spacetelescope.org. Retrieved 26 February 2018.

[19] Slipher, V. M. (1913). "The Radial Velocity of the Andromeda Nebula". Lowell Observatory Bulletin. 1 (8): 56–57. Bibcode:1913LowOB...2...56S.

[20] Slipher, V. M. (1915). "Spectrographic Observations of Nebulae". Popular Astronomy. 23: 21–24. Bibcode:1915PA.....23...21S.

[21] Friedman, A. (1922). "Über die Krümmung des Raumes". Zeitschrift für Physik (in German). 10 (1): 377–386. Bibcode:1922ZPhy...10..377F. doi:10.1007/BF01332580. S2CID 125190902. Translated to English in Friedmann, A. (1999). "On the Curvature of Space". General Relativity and Gravitation. 31 (12): 1991–2000. Bibcode:1999GReGr..31.1991F. doi:10.1023/A:1026751225741. S2CID 122950995.

[22] van den Bergh, Sydney (2011). "The Curious Case of Lemaître's Equation No. 24". Journal of the Royal Astronomical Society of Canada. 105 (4): 151. arXiv:1106.1195. Bibcode:2011JRASC.105..151V.

[23] Block, David (2012). 'Georges Lemaitre and Stigler's law of eponymy' in Georges Lemaître: Life, Science and Legacy (Holder and Mitton ed.). Springer. pp. 89–96.

[24] Sandage, Allan (December 1989). "Edwin Hubble 1889-1953". Journal of the Royal Astronomical Society of Canada. 83 (6): 351–362. Bibcode:1989JRASC..83..351S.

[Keel-25] Keel, W. C. (2007). The Road to Galaxy Formation (2nd ed.). Springer. pp. 7–8. ISBN 978-3-540-72534-3.

[Freedman2001-26] Freedman, W. L.; et al. (2001). "Final results from the Hubble Space Telescope Key Project to measure the Hubble constant". The Astrophysical Journal. 553 (1): 47–72. arXiv:astro-ph/0012376. Bibcode:2001ApJ...553...47F. doi:10.1086/320638. S2CID 119097691.

[Weinberg-27] Weinberg, S. (2008). Cosmology. Oxford University Press. p. 28. ISBN 978-0-19-852682-7.

[28] Kirshner, R. P. (2003). "Hubble's diagram and cosmic expansion". Proceedings of the National Academy of Sciences. 101 (1): 8–13. Bibcode:2003PNAS..101....8K. doi:10.1073/pnas.2536799100. PMC 314128. PMID 14695886.

[mapcc-29] "What is a Cosmological Constant?". Goddard Space Flight Center. Retrieved 2013-10-17.

[30] Isaacson, W. (2007). Einstein: His Life and Universe. Simon & Schuster. p. 354. ISBN 978-0-7432-6473-0.

[31] "Einstein's Biggest Blunder? Dark Energy May Be Consistent With Cosmological Constant". Science Daily. 28 November 2007. Retrieved 2013-06-02.

[D&L-32] Davis, T. M.; Lineweaver, C. H. (2001). "Superluminal Recessional Velocities". AIP Conference Proceedings. 555: 348–351. arXiv:astro-ph/0011070. Bibcode:2001AIPC..555..348D. CiteSeerX 10.1.1.254.1810. doi:10.1063/1.1363540. S2CID 118876362.

[33] "Is the universe expanding faster than the speed of light?". Ask an Astronomer at Cornell University. Archived from the original on 23 November 2003. Retrieved 5 June 2015.

[Harrison-34] Harrison, E. (1992). "The redshift-distance and velocity-distance laws". The Astrophysical Journal. 403: 28–31. Bibcode:1993ApJ...403...28H. doi:10.1086/172179.

[Madsen-35] Madsen, M. S. (1995). The Dynamic Cosmos. CRC Press. p. 35. ISBN 978-0-412-62300-4.

[Dekel-36] Dekel, A.; Ostriker, J. P. (1999). Formation of Structure in the Universe. Cambridge University Press. p. 164. ISBN 978-0-521-58632-0.

[Padmanabhan-37] Padmanabhan, T. (1993). Structure formation in the universe. Cambridge University Press. p. 58. ISBN 978-0-521-42486-8.

[Sartori-38] Sartori, L. (1996). Understanding Relativity. University of California Press. p. 163, Appendix 5B. ISBN 978-0-520-20029-6.

[L_Sartori-39] Sartori, L. (1996). Understanding Relativity. University of California Press. pp. 304–305. ISBN 978-0-520-20029-6.

[40] Matts Roos, 우주론 입문

[AM-20170818-41] Scharping, Nathaniel (18 October 2017). "Gravitational Waves Show How Fast The Universe is Expanding". Astronomy. Retrieved 18 October 2017.

[Chase_etal_2004-42] Chase, S. I.; Baez, J. C. (2004). "Olbers' Paradox". The Original Usenet Physics FAQ. Retrieved 2013-10-17.

[Asimov1974-43] Asimov, I. (1974). "The Black of Night". Asimov on Astronomy. Doubleday. ISBN 978-0-385-04111-9.

[44] Croton, Darren J. (14 October 2013). "Damn You, Little h! (Or, Real-World Applications of the Hubble Constant Using Observed and Simulated Data)". Publications of the Astronomical Society of Australia. 30. arXiv:1308.4150. Bibcode:2013PASA...30...52C. doi:10.1017/pasa.2013.31. S2CID 119257465. Retrieved 8 December 2021.

[45] Peebles, P. J. E. (1993). Principles of Physical Cosmology. Princeton University Press.

[46] Perlmutter, S. (2003). "Supernovae, Dark Energy, and the Accelerating Universe" (PDF). Physics Today. 56 (4): 53–60. Bibcode:2003PhT....56d..53P. CiteSeerX 10.1.1.77.7990. doi:10.1063/1.1580050. Archived (PDF) from the original on 2022-10-09.

[47] Carroll, Sean (2004). Spacetime and Geometry: An Introduction to General Relativity (illustrated ed.). San Francisco: Addison-Wesley. p. 328. ISBN 978-0-8053-8732-2.

[48] Heneka, C.; Amendola, L. (2018). "General modified gravity with 21cm intensity mapping: simulations and forecast". Journal of Cosmology and Astroparticle Physics. 2018 (10): 004. arXiv:1805.03629. Bibcode:2018JCAP...10..004H. doi:10.1088/1475-7516/2018/10/004. S2CID 119224326.

[49] Tawfik, A.; Harko, T. (2012). "Quark-hadron phase transitions in the viscous early universe". Physical Review D. 85 (8): 084032. arXiv:1108.5697. Bibcode:2012PhRvD..85h4032T. doi:10.1103/PhysRevD.85.084032. S2CID 73716828.

[50] Tawfik, A. (2011). "The Hubble parameter in the early universe with viscous QCD matter and finite cosmological constant". Annalen der Physik. 523 (5): 423–434. arXiv:1102.2626. Bibcode:2011AnP...523..423T. doi:10.1002/andp.201100038. S2CID 118500485.

[51] Tawfik, A.; Wahba, M.; Mansour, H.; Harko, T. (2011). "Viscous quark-gluon plasma in the early universe". Annalen der Physik. 523 (3): 194–207. arXiv:1001.2814. Bibcode:2011AnP...523..194T. doi:10.1002/andp.201000052. S2CID 119271582.

[52] Hawley, John F.; Holcomb, Katherine A. (2005). Foundations of modern cosmology (2nd ed.). Oxford [u.a.]: Oxford University Press. p. 304. ISBN 978-0-19-853096-1.

[planck_overview-53] Bucher, P. A. R.; et al. (Planck Collaboration) (2013). "Planck 2013 results. I. Overview of products and scientific Results". Astronomy & Astrophysics. 571: A1. arXiv:1303.5062. Bibcode:2014A&A...571A...1P. doi:10.1051/0004-6361/201321529. S2CID 218716838.

[LS-20190826-54] Mann, Adam (26 August 2019). "One Number Shows Something Is Fundamentally Wrong with Our Conception of the Universe – This fight has universal implications". Live Science. Retrieved 26 August 2019.

[di_Valentino_2021_153001-55] ^ ^a ^b ^c ^d ^e ^f di Valentino, Eleonora; et al. (2021). "In the realm of the Hubble tension—a review of solutions". Classical and Quantum Gravity. 38 (15): 153001. arXiv:2103.01183. Bibcode:2021CQGra..38o3001D. doi:10.1088/1361-6382/ac086d. S2CID 232092525.

[56] Gresko, Michael (17 December 2021). "The universe is expanding faster than it should be". National Geographic. Archived from the original on December 17, 2021. Retrieved 21 December 2021.

[SA-20230914-58] Starr, Michelle (14 September 2023). "JWST Just Measured The Expansion Rate of The Universe. Astronomers Are Stumped". ScienceAlert. Archived from the original on 16 September 2023. Retrieved 16 September 2023.

[Snowmass21-60] Abdalla, Elcio; Abellán, Guillermo Franco; Aboubrahim, Amin (11 Mar 2022), "Cosmology Intertwined: A Review of the Particle Physics, Astrophysics, and Cosmology Associated with the Cosmological Tensions and Anomalies", Journal of High Energy Astrophysics, 34: 49, arXiv:2203.06142v1, Bibcode:2022JHEAp..34...49A, doi:10.1016/j.jheap.2022.04.002, S2CID 247411131

[61] Rameez, Mohamed; Sarkar, Subir (15 July 2021). "Is there really a Hubble tension?". Classical and Quantum Gravity. 38 (15): 154005. arXiv:1911.06456. Bibcode:2021CQGra..38o4005R. doi:10.1088/1361-6382/ac0f39. ISSN 0264-9381. S2CID 208075753.

[62] Singh, Ritesh (28 October 2021). "Evidence for possible systematic underestimation of uncertainties in extragalactic distances and its cosmological implications". Astrophysics and Space Science. 366 (10): 99. arXiv:2111.07872. Bibcode:2021Ap&SS.366...99S. doi:10.1007/s10509-021-04006-5. ISSN 1572-946X. S2CID 240179422.

[Haslbauer-63] Haslbauer, M.; Banik, I.; Kroupa, P. (2020-12-21). "The KBC void and Hubble tension contradict LCDM on a Gpc scale – Milgromian dynamics as a possible solution". Monthly Notices of the Royal Astronomical Society. 499 (2): 2845–2883. arXiv:2009.11292. Bibcode:2020MNRAS.499.2845H. doi:10.1093/mnras/staa2348. ISSN 0035-8711.

[65] Poulin, Vivian; Smith, Tristan L.; Karwal, Tanvi; Kamionkowski, Marc (2019-06-04). "Early Dark Energy can Resolve the Hubble Tension". Physical Review Letters. 122 (22): 221301. arXiv:1811.04083. Bibcode:2019PhRvL.122v1301P. doi:10.1103/PhysRevLett.122.221301. PMID 31283280. S2CID 119233243.

[67] Zhao, Gong-Bo; Raveri, Marco; Pogosian, Levon; Wang, Yuting; Crittenden, Robert G.; Handley, Will J.; Percival, Will J.; Beutler, Florian; Brinkmann, Jonathan; Chuang, Chia-Hsun; Cuesta, Antonio J.; Eisenstein, Daniel J.; Kitaura, Francisco-Shu; Koyama, Kazuya; l'Huillier, Benjamin; Nichol, Robert C.; Pieri, Matthew M.; Rodriguez-Torres, Sergio; Ross, Ashley J.; Rossi, Graziano; Sánchez, Ariel G.; Shafieloo, Arman; Tinker, Jeremy L.; Tojeiro, Rita; Vazquez, Jose A.; Zhang, Hanyu (2017). "Dynamical dark energy in light of the latest observations". Nature Astronomy. 1 (9): 627–632. arXiv:1701.08165. doi:10.1038/s41550-017-0216-z. S2CID 256705070.

[68] Berezhiani, Zurab; Dolgov, A. D.; Tkachev, I. I. (2015). "Reconciling Planck results with low redshift astronomical measurements". Physical Review D. 92 (6): 061303. arXiv:1505.03644. doi:10.1103/PhysRevD.92.061303. S2CID 118169478.

[69] Laila Linke (17 May 2021). "Solving the Hubble tension might require more than changing the early Universe". Astrobites.

[70] Vagnozzi, Sunny (2023-08-30). "Seven Hints That Early-Time New Physics Alone Is Not Sufficient to Solve the Hubble Tension". Universe. 9 (9): 393. arXiv:2308.16628. Bibcode:2023Univ....9..393V. doi:10.3390/universe9090393.

[71] Ryan E. Keeley and Arman Shafieloo (August 2023). "Ruling Out New Physics at Low Redshift as a Solution to the H₀ Tension". Physical Review Letters. 131 (11): 111002. arXiv:2206.08440. doi:10.1103/PhysRevLett.131.111002. PMID 37774270. S2CID 249848075.

[72] Baade, W. (1944) 메시에 32의 해상도, NGC 205, 안드로메다 성운의 중심 영역. ApJ 100 137–146

[73] Baade, W. (1956) 세페이드족의 주기-광도 관계. PASP 68 5–16

[74] Allen, Nick. "Section 2: The Great Debate and the Great Mistake: Shapley, Hubble, Baade". The Cepheid Distance Scale: A History. Archived from the original on 10 December 2007. Retrieved 19 November 2011.

[Overbye-75] Overbye, D. (1999). "Prologue". Lonely Hearts of the Cosmos (2nd ed.). HarperCollins. p. 1ff. ISBN 978-0-316-64896-7.

[:0-76] Vaucouleurs, G. (1982). The cosmic distance scale and the Hubble constant. Mount Stromlo and Siding Spring Observatories, Australian National University.

[SA2019-77] Ananthaswamy, Anil (22 March 2019). "Best-Yet Measurements Deepen Cosmological Crisis". Scientific American. Retrieved 23 March 2019.

[Riess2019-78] Riess, Adam G.; Casertano, Stefano; Yuan, Wenlong; Macri, Lucas M.; Scolnic, Dan (18 March 2019). "Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics Beyond LambdaCDM". The Astrophysical Journal. 876 (1): 85. arXiv:1903.07603. Bibcode:2019ApJ...876...85R. doi:10.3847/1538-4357/ab1422. S2CID 85528549.

[79] Millea, Marius; Knox, Lloyd (2019-08-10). "The Hubble Hunter's Guide". arXiv:1908.03663v1 [astro-ph.CO].

[PHYS-20181022-80] Lerner, Louise (22 October 2018). "Gravitational waves could soon provide measure of universe's expansion". Phys.org. Retrieved 22 October 2018.

[NAT-20181017-81] Chen, Hsin-Yu; Fishbach, Maya; Holz, Daniel E. (17 October 2018). "A two per cent Hubble constant measurement from standard sirens within five years". Nature. 562 (7728): 545–547. arXiv:1712.06531. Bibcode:2018Natur.562..545C. doi:10.1038/s41586-018-0606-0. PMID 30333628. S2CID 52987203.

[EA-20190708-82] National Radio Astronomy Observatory (8 July 2019). "New method may resolve difficulty in measuring universe's expansion – Neutron star mergers can provide new 'cosmic ruler'". EurekAlert!. Retrieved 8 July 2019.

[NRAO-20190708-83] Finley, Dave (8 July 2019). "New Method May Resolve Difficulty in Measuring Universe's Expansion". National Radio Astronomy Observatory. Retrieved 8 July 2019.

[NAT-20190708-84] Hotokezaka, K.; et al. (8 July 2019). "A Hubble constant measurement from superluminal motion of the jet in GW170817". Nature Astronomy. 3 (10): 940–944. arXiv:1806.10596. Bibcode:2019NatAs...3..940H. doi:10.1038/s41550-019-0820-1. S2CID 119547153.

[EA-20190716-85] Carnegie Institution of Science (16 July 2019). "New measurement of universe's expansion rate is 'stuck in the middle' – Red giant stars observed by Hubble Space Telescope used to make an entirely new measurement of how fast the universe is expanding". EurekAlert!. Retrieved 16 July 2019.

[SCI-20190719-86] Sokol, Joshua (19 July 2019). "Debate intensifies over speed of expanding universe". Science. doi:10.1126/science.aay8123. S2CID 200021863. Retrieved 20 July 2019.

[The_Carnegie-Chicago_Hubble_Program-87] Freedman, Wendy L.; Madore, Barry F.; Hatt, Dylan; Hoyt, Taylor J.; Jang, In-Sung; Beaton, Rachael L.; et al. (2019). "The Carnegie-Chicago Hubble Program. VIII. An Independent Determination of the Hubble Constant Based on the Tip of the Red Giant Branch". The Astrophysical Journal. 882 (1): 34. arXiv:1907.05922. Bibcode:2019ApJ...882...34F. doi:10.3847/1538-4357/ab2f73. S2CID 196623652.

[megamaser-88] Pesce, D. W.; Braatz, J. A.; Reid, M. J.; Riess, A. G.; et al. (26 February 2020). "The Megamaser Cosmology Project. XIII. Combined Hubble Constant Constraints". The Astrophysical Journal. 891 (1): L1. arXiv:2001.09213. Bibcode:2020ApJ...891L...1P. doi:10.3847/2041-8213/ab75f0. S2CID 210920444.

[89] Castelvecchi, Davide (2020-07-15). "Mystery over Universe's expansion deepens with fresh data". Nature. 583 (7817): 500–501. Bibcode:2020Natur.583..500C. doi:10.1038/d41586-020-02126-6. PMID 32669728. S2CID 220583383.

[90] SPT-3G Collaboration; Balkenhol, L.; Dutcher, D.; Spurio Mancini, A.; Doussot, A.; Benabed, K.; Galli, S.; Ade, P. A. R.; Anderson, A. J.; Ansarinejad, B.; Archipley, M.; Bender, A. N.; Benson, B. A.; Bianchini, F.; Bleem, L. E. (2023-07-13). "Measurement of the CMB temperature power spectrum and constraints on cosmology from the SPT-3G 2018 $TT$, $TE$, and $EE$ dataset". Physical Review D. 108 (2): 023510. arXiv:2212.05642v3. doi:10.1103/PhysRevD.108.023510. S2CID 259887685.{{cite journal}}: CS1 main: 숫자 이름: 저자 목록 (링크)

[91] Kelly, P. L.; Rodney, S.; Treu, T.; Oguri, M.; Chen, W.; Zitri, A.; et al. (2023-05-11). "Constraints on the Hubble constant from Supernova Refsdal's reappearance". Science. 380 (6649): eabh1322. arXiv:2305.06367. Bibcode:2023Sci...380.1322K. doi:10.1126/science.abh1322. PMID 37167351. S2CID 258615332.

[92] Contarini, Sofia; Pisani, Alice; Hamaus, Nico; Marulli, Federico; Moscardini, Lauro; Baldi, Marco (2022). "Voids fill us in on rising cosmology tensions". arXiv:2212.07438 [astro-ph.CO].

[93] Chiou, Lyndie (2023-07-25). "How (Nearly) Nothing Might Solve Cosmology's Biggest Questions". Quanta Magazine. Retrieved 2023-07-31.

[94] Brout, Dillon; Scolnic, Dan; Popovic, Brodie; Riess, Adam G.; Carr, Anthony; Zuntz, Joe; Kessler, Rick; Davis, Tamara M.; Hinton, Samuel; Jones, David; Kenworthy, W. D'Arcy; Peterson, Erik R.; Said, Khaled; Taylor, Georgie; Ali, Noor; Armstrong, Patrick; Charvu, Pranav; Dwomoh, Arianna; Meldorf, Cole; Palmese, Antonella; Qu, Helen; Rose, Benjamin M.; Sanchez, Bruno; Stubbs, Christopher W.; Vincenzi, Maria; Wood, Charlotte M.; Brown, Peter J.; Chen, Rebecca; Chambers, Ken; Coulter, David A.; Dai, Mi; Dimitriadis, Georgios; Filippenko, Alexi V.; Foley, Ryan J.; Jha, Saurabh W.; Kelsey, Lisa; Kirshner, Robert P.; Möller, Anais; Muir, Jessie; Nadathur, Seshadri; Pan, Yen-Chen; Rest, Armin; Rojas-Bravo, Cesar; Sako, Masao; Siebert, Matthew R.; Smith, Mat; Stahl, Benjamin E.; Wiseman, Phil (2022-02-08). "The Pantheon+ Analysis: Cosmological Constraints". The Astrophysical Journal. 938 (2): 110. arXiv:2202.04077. Bibcode:2022ApJ...938..110B. doi:10.3847/1538-4357/ac8e04. S2CID 246679941.

[deJaeger2022-95] Jaeger, T.; Galbany, L.; Riess, A. G.; Stahl, Ben E.; et al. (17 June 2022). "A 5 per cent measurement of the Hubble–Lemaître constant from Type II supernovae". MNRAS. 514 (3): 4620–4628. arXiv:2203.08974. doi:10.1093/mnras/stac1661.

[96] Riess, Adam G.; Yuan, Wenlong; Macri, Lucas M.; Scolnic, Dan; Brout, Dillon; Casertano, Stefano; Jones, David O.; Murakami, Yukei; Breuval, Louise; Brink, Thomas G.; Filippenko, Alexei V. (2021-12-08). "A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km/s/Mpc Uncertainty from the Hubble Space Telescope and the SH0ES Team". The Astrophysical Journal. 934 (1). arXiv:2112.04510. Bibcode:2022ApJ...934L...7R. doi:10.3847/2041-8213/ac5c5b. S2CID 245005861.

[97] Freedman, Wendy L. (2021-09-01). "Measurements of the Hubble Constant: Tensions in Perspective*". The Astrophysical Journal. 919 (1): 16. arXiv:2106.15656. Bibcode:2021ApJ...919...16F. doi:10.3847/1538-4357/ac0e95. ISSN 0004-637X. S2CID 235683396.

[Soltis2020-98] Soltis, J.; Casertano, S.; Riess, A. G. (2021). "The Parallax of Omega Centauri Measured from Gaia EDR3 and a Direct, Geometric Calibration of the Tip of the Red Giant Branch and the Hubble Constant". The Astrophysical Journal. 908 (1): L5. arXiv:2012.09196. Bibcode:2021ApJ...908L...5S. doi:10.3847/2041-8213/abdbad. S2CID 229297709.

[Riess2020-99] Riess, A. G.; Casertano, S.; Yuan, W.; Bowers, J. B.; et al. (2021). "Cosmic Distances Calibrated to 1% Precision with Gaia EDR3 Parallaxes and Hubble Space Telescope Photometry of 75 Milky Way Cepheids Confirm Tension with LambdaCDM". The Astrophysical Journal. 908 (1): L6. arXiv:2012.08534. Bibcode:2021ApJ...908L...6R. doi:10.3847/2041-8213/abdbaf. S2CID 229213131.

[Baxter2020-100] Baxter, E. J.; Sherwin, B. D. (February 2021). "Determining the Hubble constant without the sound horizon scale: measurements from CMB lensing". Monthly Notices of the Royal Astronomical Society. 501 (2): 1823–1835. arXiv:2007.04007. Bibcode:2021MNRAS.501.1823B. doi:10.1093/mnras/staa3706. S2CID 220404332.

[Denzel2020-101] Denzel, P.; Coles, J. P.; Saha, P.; Williams, L. L. R. (February 2021). "The Hubble constant from eight time-delay galaxy lenses". Monthly Notices of the Royal Astronomical Society. 501 (1): 784–801. arXiv:2007.14398. Bibcode:2021MNRAS.501..784D. doi:10.1093/mnras/staa3603. S2CID 220845622.

[102] Sedgwick, Thomas M; Collins, Chris A; Baldry, Ivan K; James, Philip A (2020-11-07). "The effects of peculiar velocities in SN Ia environments on the local H0 measurement". Monthly Notices of the Royal Astronomical Society. 500 (3): 3728–3742. arXiv:1911.03155. doi:10.1093/mnras/staa3456. ISSN 0035-8711.

[103] Anderson, Lauren; Aubourg, Éric; Bailey, Stephen; Beutler, Florian; Bhardwaj, Vaishali; Blanton, Michael; Bolton, Adam S.; Brinkmann, J.; Brownstein, Joel R.; Burden, Angela; Chuang, Chia-Hsun (2014-04-21). "The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: baryon acoustic oscillations in the Data Releases 10 and 11 Galaxy samples". Monthly Notices of the Royal Astronomical Society. 441 (1): 24–62. doi:10.1093/mnras/stu523. hdl:2445/101758. ISSN 1365-2966.

[Mukherjee2020-104] Mukherjee, S.; Ghosh, A.; Graham, M. J.; Karathanasis, C.; et al. (29 September 2020). "First measurement of the Hubble parameter from bright binary black hole GW190521". arXiv:2009.14199 [astro-ph.CO].

[deJaeger2020-105] Jaeger, T.; Stahl, B.; Zheng, W.; Filippenko, A.V.; et al. (18 June 2020). "A measurement of the Hubble constant from Type II supernovae". MNRAS. 496 (3): 3402–3411. arXiv:2006.03412. doi:10.1093/mnras/staa1801.

[106] Shajib, A. J.; Birrer, S.; Treu, T.; Agnello, A.; et al. (14 October 2019). "STRIDES: A 3.9 per cent measurement of the Hubble constant from the strongly lensed system DES J0408-5354". Monthly Notices of the Royal Astronomical Society. arXiv:1910.06306. doi:10.1093/mnras/staa828. S2CID 204509190.

[107] Chen, G.C.-F.; Fassnacht, C.D.; Suyu, S.H.; Rusu, C.E.; et al. (12 September 2019). "A SHARP view of H0LiCOW: H0 from three time-delay gravitational lens systems with adaptive optics imaging". Monthly Notices of the Royal Astronomical Society. 490 (2): 1743–1773. arXiv:1907.02533. Bibcode:2019MNRAS.490.1743C. doi:10.1093/mnras/stz2547. S2CID 195820422.

[108] Dutta, Koushik; Roy, Anirban; Ruchika, Ruchika; Sen, Anjan A.; Sheikh-Jabbari, M. M. (20 August 2019). "Cosmology With Low-Redshift Observations: No Signal For New Physics". Phys. Rev. D. 100 (10): 103501. arXiv:1908.07267. Bibcode:2019PhRvD.100j3501D. doi:10.1103/PhysRevD.100.103501. S2CID 201107151.

[109] Reid, M. J.; Pesce, D. W.; Riess, A. G. (15 August 2019). "An Improved Distance to NGC 4258 and its Implications for the Hubble Constant". The Astrophysical Journal. 886 (2): L27. arXiv:1908.05625. Bibcode:2019ApJ...886L..27R. doi:10.3847/2041-8213/ab552d. S2CID 199668809.

[H0LiCOW2019-110] Kenneth C. Wong (2020). "H0LiCOW XIII. A 2.4% measurement of H₀ from lensed quasars: 5.3σ tension between early and late-Universe probes". Monthly Notices of the Royal Astronomical Society. arXiv:1907.04869. doi:10.1093/mnras/stz3094. S2CID 195886279.

[111] Domínguez, Alberto; et al. (28 March 2019). "A new measurement of the Hubble constant and matter content of the Universe using extragalactic background light γ-ray attenuation". The Astrophysical Journal. 885 (2): 137. arXiv:1903.12097. Bibcode:2019ApJ...885..137D. doi:10.3847/1538-4357/ab4a0e. S2CID 85543845.

[Ryan2019-112] Ryan, Joseph; Chen, Yun; Ratra, Bharat (8 February 2019). "Baryon acoustic oscillation, Hubble parameter, and angular size measurement constraints on the Hubble constant, dark energy dynamics, and spatial curvature". Monthly Notices of the Royal Astronomical Society. 488 (3): 3844–3856. arXiv:1902.03196. Bibcode:2019MNRAS.488.3844R. doi:10.1093/mnras/stz1966. S2CID 119226802.

[DES-113] Macaulay, E; et al. (DES collaboration) (2018). "First Cosmological Results using Type Ia Supernovae from the Dark Energy Survey: Measurement of the Hubble Constant". Monthly Notices of the Royal Astronomical Society. 486 (2): 2184–2196. arXiv:1811.02376. doi:10.1093/mnras/stz978. S2CID 119310644.

[H0LiCOW-114] Birrer, S.; Treu, T.; Rusu, C. E.; Bonvin, V.; Fassnacht, C. D.; Chan, J. H. H.; et al. (2018). "H0LiCOW – IX. Cosmographic analysis of the doubly imaged quasar SDSS 1206+4332 and a new measurement of the Hubble constant". Monthly Notices of the Royal Astronomical Society. 484 (4): 4726–4753. arXiv:1809.01274. Bibcode:2019MNRAS.484.4726B. doi:10.1093/mnras/stz200. S2CID 119053798.

[2018planckcosmos-115] Planck Collaboration; Aghanim, N.; et al. (2018). "Planck 2018 results. VI. Cosmological parameters". arXiv:1807.06209. Bibcode:2018arXiv180706209P.

[gaiariess2018-116] Riess, Adam G.; Casertano, Stefano; Yuan, Wenlong; Macri, Lucas; et al. (2018). "Milky Way Cepheid Standards for Measuring Cosmic Distances and Application to Gaia DR2: Implications for the Hubble Constant". The Astrophysical Journal. 861 (2): 126. arXiv:1804.10655. Bibcode:2018ApJ...861..126R. doi:10.3847/1538-4357/aac82e. ISSN 0004-637X. S2CID 55643027.

[guardianhubbleconstant-117] Devlin, Hannah (10 May 2018). "The answer to life, the universe and everything might be 73. Or 67". the Guardian. Retrieved 13 May 2018.

[118] Riess, Adam G.; Casertano, Stefano; Yuan, Wenlong; Macri, Lucas; et al. (22 February 2018). "New parallaxes of galactic Cepheids from spatially scanning the Hubble Space Telescope: Implications for the Hubble constant" (PDF). The Astrophysical Journal. 855 (2): 136. arXiv:1801.01120. Bibcode:2018ApJ...855..136R. doi:10.3847/1538-4357/aaadb7. S2CID 67808349. Archived (PDF) from the original on 2022-10-09. Retrieved 23 February 2018.

[NASA-20180222-119] Weaver, Donna; Villard, Ray; Hille, Karl (22 February 2018). "Improved Hubble Yardstick Gives Fresh Evidence for New Physics in the Universe". NASA. Retrieved 24 February 2018.

[120] The LIGO Scientific Collaboration and The Virgo Collaboration; The 1M2H Collaboration; The Dark Energy Camera GW-EM Collaboration and the DES Collaboration; The DLT40 Collaboration; et al. (2017-10-16). "A gravitational-wave standard siren measurement of the Hubble constant" (PDF). Nature. 551 (7678): 85–88. arXiv:1710.05835. Bibcode:2017Natur.551...85A. doi:10.1038/nature24471. ISSN 1476-4687. PMID 29094696. S2CID 205261622. Archived (PDF) from the original on 2022-10-09.{{cite journal}}: CS1 main: 숫자 이름: 저자 목록 (링크)

[121] Feeney, Stephen M; Peiris, Hiranya V; Williamson, Andrew R; Nissanke, Samaya M; et al. (2019). "Prospects for resolving the Hubble constant tension with standard sirens". Physical Review Letters. 122 (6): 061105. arXiv:1802.03404. Bibcode:2019PhRvL.122f1105F. doi:10.1103/PhysRevLett.122.061105. hdl:2066/201510. PMID 30822066. S2CID 73493934.

[VitaleChen2018-122] Vitale, Salvatore; Chen, Hsin-Yu (12 July 2018). "Measuring the Hubble Constant with Neutron Star Black Hole Mergers". Physical Review Letters. 121 (2): 021303. arXiv:1804.07337. Bibcode:2018PhRvL.121b1303V. doi:10.1103/PhysRevLett.121.021303. hdl:1721.1/117110. PMID 30085719. S2CID 51940146.

[123] Bonvin, Vivien; Courbin, Frédéric; Suyu, Sherry H.; et al. (2016-11-22). "H0LiCOW – V. New COSMOGRAIL time delays of HE 0435−1223: H₀ to 3.8 per cent precision from strong lensing in a flat ΛCDM model". MNRAS. 465 (4): 4914–4930. arXiv:1607.01790. Bibcode:2017MNRAS.465.4914B. doi:10.1093/mnras/stw3006. S2CID 109934944.

[Cosmicflows-3-124] Tully, R. Brent; Courtois, Hélène M.; Sorce, Jenny G. (3 August 2016). "COSMICFLOWS-3". The Astronomical Journal. 152 (2): 50. arXiv:1605.01765. Bibcode:2016AJ....152...50T. doi:10.3847/0004-6256/152/2/50. S2CID 250737862.

[125] Grieb, Jan N.; Sánchez, Ariel G.; Salazar-Albornoz, Salvador (2016-07-13). "The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological implications of the Fourier space wedges of the final sample". Monthly Notices of the Royal Astronomical Society. 467 (2): stw3384. arXiv:1607.03143. Bibcode:2017MNRAS.467.2085G. doi:10.1093/mnras/stw3384. S2CID 55888085.

[ebossinfo-126] "The Extended Baryon Oscillation Spectroscopic Survey (eBOSS)". SDSS. Retrieved 13 May 2018.

[127] Riess, Adam G.; Macri, Lucas M.; Hoffmann, Samantha L.; Scolnic, Dan; et al. (2016-04-05). "A 2.4% Determination of the Local Value of the Hubble Constant". The Astrophysical Journal. 826 (1): 56. arXiv:1604.01424. Bibcode:2016ApJ...826...56R. doi:10.3847/0004-637X/826/1/56. S2CID 118630031.

[planckesa2015-128] "Planck Publications: Planck 2015 Results". European Space Agency. February 2015. Retrieved 9 February 2015.

[nature20141202-129] Cowen, Ron; Castelvecchi, Davide (2 December 2014). "European probe shoots down dark-matter claims". Nature. doi:10.1038/nature.2014.16462. Retrieved 6 December 2014.

[cosmicflows2-130] Tully, R. Brent; Courtois, Helene M.; Dolphin, Andrew E.; Fisher, J. Richard; et al. (5 September 2013). "Cosmicflows-2: The Data". The Astronomical Journal. 146 (4): 86. arXiv:1307.7213. Bibcode:2013AJ....146...86T. doi:10.1088/0004-6256/146/4/86. ISSN 0004-6256. S2CID 118494842.

[ESA-20130321-131] "Planck reveals an almost perfect universe". ESA. 21 March 2013. Retrieved 2013-03-21.

[NASA-20130321-132] "Planck Mission Brings Universe Into Sharp Focus". JPL. 21 March 2013. Retrieved 2013-03-21.

[NYT-20130321-133] Overbye, D. (21 March 2013). "An infant universe, born before we knew". New York Times. Retrieved 2013-03-21.

[NBC-20130321-134] Boyle, A. (21 March 2013). "Planck probe's cosmic 'baby picture' revises universe's vital statistics". NBC News. Archived from the original on 2013-03-23. Retrieved 2013-03-21.

[135] Bennett, C. L.; et al. (2013). "Nine-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Final maps and results". The Astrophysical Journal Supplement Series. 208 (2): 20. arXiv:1212.5225. Bibcode:2013ApJS..208...20B. doi:10.1088/0067-0049/208/2/20. S2CID 119271232.

[wmap7parameters-136] Jarosik, N.; et al. (2011). "Seven-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Sky maps, systematic errors, and basic results". The Astrophysical Journal Supplement Series. 192 (2): 14. arXiv:1001.4744. Bibcode:2011ApJS..192...14J. doi:10.1088/0067-0049/192/2/14. S2CID 46171526.

[137] 다양한 모델을 WMAP 및 기타 데이터의 여러 조합에 맞게 조정하여 얻은₀ H 및 기타 우주론적 매개변수에 대한 결과는 NASA의 LAMDA 웹사이트인 Archive the Wayback Machine 2014-07-09에서 확인할 수 있습니다.

[WMAP2009-138] Hinshaw, G.; et al. (WMAP Collaboration) (2009). "Five-year Wilkinson Microwave Anisotropy Probe observations: Data processing, sky maps, and basic results". The Astrophysical Journal Supplement. 180 (2): 225–245. arXiv:0803.0732. Bibcode:2009ApJS..180..225H. doi:10.1088/0067-0049/180/2/225. S2CID 3629998.

[139] Spergel, D. N.; et al. (WMAP Collaboration) (2007). "Three-year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Implications for cosmology". The Astrophysical Journal Supplement Series. 170 (2): 377–408. arXiv:astro-ph/0603449. Bibcode:2007ApJS..170..377S. doi:10.1086/513700. S2CID 1386346.

[140] Bonamente, M.; Joy, M. K.; Laroque, S. J.; Carlstrom, J. E.; et al. (2006). "Determination of the cosmic distance scale from Sunyaev–Zel'dovich effect and Chandra X‐ray measurements of high‐redshift galaxy clusters". The Astrophysical Journal. 647 (1): 25. arXiv:astro-ph/0512349. Bibcode:2006ApJ...647...25B. doi:10.1086/505291. S2CID 15723115.

[planck2013_parameters-141] Planck Collaboration (2013). "Planck 2013 results. XVI. Cosmological parameters". Astronomy & Astrophysics. 571: A16. arXiv:1303.5076. Bibcode:2014A&A...571A..16P. doi:10.1051/0004-6361/201321591. S2CID 118349591.

[142] Spergel, D.N. (September 2003). "First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters". The Astrophysical Journal Supplement Series. 148 (1): 175–194. arXiv:astro-ph/0302209. Bibcode:2003ApJS..148..175S. doi:10.1086/377226. S2CID 10794058.

[143] Riess, Adam G. (January 1995). "Using SN Ia Light Curve Shapes to Measure The Hubble Constant". The Astrophysical Journal. 438 (L17). arXiv:astro-ph/9410054. doi:10.1086/187704. S2CID 118938423.

[cfa-144] John P. Huchra (2008). "The Hubble Constant". Harvard Center for Astrophysics.

[145] Sandage, A. R. (1958). "Current problems in the extragalactic distance scale". The Astrophysical Journal. 127 (3): 513–526. Bibcode:1958ApJ...127..513S. doi:10.1086/146483.

[146] 에드윈 허블, 은하 외 성운 사이의 거리와 반지름 속도의 관계, 미국 국립과학원 회보, vol. 15, No. 3, pp. 168-173, 1929년 3월

[wwu-147] "Hubble's Constant". Skywise Unlimited – Western Washington University.

[148] Lemaître, Georges (1927). "Un Univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extra-galactiques". Annales de la Société Scientifique de Bruxelles (in French). A47: 49–59. Bibcode:1927ASSB...47...49L.

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[24]

[25]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[46]

[49]

[50]

[51]

[52]

[53]

[54]

[55]

[56]

[a]

[b]

[58]

[59]

[60]

[61]

[c]

[62]

[d]

[63]

[64]

[65]

[66]

[67]

[68]

[69]

[70]

[71]

[72]

[73]

[75]

[76]

[77]

[78]

[79]

[80]

[81]

[82]

[83]

[84]

[85]

[86]

[87]

[88]

[89]

[90]

[91]

[92]

[93]

[94]

[95]

[96]

[97]

[98]

[100]

[101]

[102]

[103]

[104]

[105]

[106]

[107]

Search