8배법(물리학)

물리학에서, 8가지 방법은 쿼크 모델의 개발을 이끈 하드론이라고 알려진 아원자 입자의 종류에 대한 조직적인 체계입니다.미국의 물리학자 머레이 겔-만과 이스라엘의 물리학자 유발 니만은 ^[1][2][a]모두 1961년에 이 아이디어를 제안했다.이 이름은 ^[3]겔만(1961)의 논문에서 따왔으며 불교 8중 길을 암시하고 있다.

배경

1947년까지, 물리학자들은 그들이 물질의 가장 작은 조각들이 무엇인지 잘 이해할 수 있다고 믿었다.파이온, 뮤온, 가설화된 중성미자와 같은 우주선의 관측을 설명하는 데 필요한 소수의 불안정한 (즉, 방사성 붕괴를 겪는) 외래 입자와 함께 전자, 양성자, 중성자, 광자(원자와 빛과 같은 일상 경험의 대부분을 구성하는 성분)가 있었다.게다가, 양전자의 발견은 그들 각각에 반입자가 있을 수 있다는 것을 암시했다.원자핵에서 정전기적 반발을 극복하기 위해서는 "강력한 상호작용"이 존재해야 한다고 알려져 있었다.모든 입자가 이 강한 힘에 의해 영향을 받는 것은 아니지만, 강입자라고 불리는 입자는 이제 중간자(중질량)와 중입자(중량)로 더 분류됩니다.

그러나 1947년 말 (중립) 카온의 발견과 1949년 양전하를 띤 카온의 후속 발견은 중간자 패밀리를 예상치 못한 방식으로 확장시켰고 1950년 람다 입자는 바리온 패밀리에 같은 일을 했습니다.이 입자들은 생성되는 것보다 훨씬 더 느리게 부패하는데, 이는 1952년 에이브러햄 파이스가 제안한 것과 같이 두 가지 다른 물리적 과정이 관련되어 있다는 것을 암시한다.그리고 1953년, M. Gell Mann과 일본의 공동 연구자인 Tadao Nakano와 Kazuhiko Nishijima는 알려진 입자의 ^[4][5][b]증가하는 수집을 이해하기 위해 노력하면서 독자적으로 현재 "이상함"으로 알려진 새로운 보존 가치를 제안했다.새로운 중간자와 중입자를 발견하는 추세는 알려진 "원소" 입자의 수가 늘어나면서 1950년대까지 계속될 것이다.물리학자들은 강한 상호작용을 통해 강입자-강입자 상호작용을 이해하는 데 관심이 있었다.1932년 베르너 하이젠베르크가 중성자를 발견한 직후에 도입한 이소스핀의 개념은 몇몇 강입자를 "다중자"로 묶는 데 사용되었지만 아직까지 강입자 전체를 다루는 성공적인 과학 이론은 없었다.이것은 입자 동물원으로 알려진 입자 물리학의 혼란스러운 시기의 시작이었다.8가지 방법은 결국 쿼크 모델 솔루션을 향한 중요한 발걸음이 되었습니다.

조직

집단 표현 이론은 8가지 방법 뒤에 있는 수학적 기초이지만, 이 다소 기술적인 수학은 입자를 어떻게 구성하는데 도움을 주는지를 이해하기 위해 필요하지 않습니다.입자는 중간자 또는 중입자로 분류됩니다.각 그룹 내에서, 그들은 스핀 각 운동량에 의해 더욱 분리된다.대칭 패턴은 이러한 입자 그룹이 전하에 대해 이상함을 표시할 때 나타납니다.(이것은 오늘날 이러한 플롯을 만드는 가장 일반적인 방법이지만, 원래 물리학자들은 과전하와 동위원소 스핀이라고 불리는 동등한 특성 쌍을 사용했고, 후자는 현재 이소스핀으로 알려져 있습니다.)이러한 패턴의 대칭은 입자 간의 강한 상호작용의 근본적인 대칭을 암시합니다.아래 그림에서 같은 수평선을 따라 있는 입자를 나타내는 점들은 동일한 이상도 s를 공유하는 반면, 동일한 왼쪽 대각선 상의 점들은 동일한 전하 q(기본 전하의 배수로서 주어짐)를 공유한다.

중간자

원래의 8중 방식대로 중간자는 옥텟과 홑겹으로 구성되었다.이것은 8배 방식과 그것이 영감을 준 쿼크 모델 사이의 미세한 차이점들 중 하나이며, 이것은 중간자가 논셋(9인 그룹)으로 그룹화되어야 한다는 것을 암시한다.

중간자 옥텟

8배 방법은 가장 낮은 스핀 0 중간자 중 8개를 ^[1][6]옥텟으로 구성합니다.다음과 같은 것이 있습니다.

• 
  K⁰
  , K⁺
  , K⁻
  , K⁰
  kons
• ", " 및^{0
  −}
  "
  pion⁺
  "
• 
  η
  

다이어그램에서 정반대 입자는 서로 반대입자이며, 중앙의 입자는 서로 반대입자입니다.

중간자 단품

숯도 없고 목도 없는 에타 프라임 중간자는 원래 단일트로 분류되었습니다.

• 
  η′
  

나중에 개발된 쿼크 모델에서는 앞에서 언급한 바와 같이 중간자 노넷의 일부로 더 잘 볼 수 있다.

바리온스

바리온 옥텟

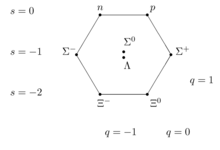
8배 방법은 스핀 1/2 바리온을 옥텟으로 구성합니다.구성 요소는 다음과 같습니다.

• 중성자(n)와 양성자(p)
• 
  δ^{−
  0}
  , δ 및⁺
  δ 시그마 바리온
• 
  기묘한⁰
  람다 바리온
• 
  ξ⁻
  및⁰
  xi xi 바리온

바리온 십중창

8배법의 조직원칙은 스핀-3/2 바리온에도 적용되어 십중창을 형성한다.

• 
  δ^{−
  0}
  , δ⁺
  , δ 및⁺⁺
  δ 델타 바리온
• 
  δ^{∗−
  ∗0}
  , δ 및^∗+
  δ 시그마 바리온
• 
  ξ^∗−
  및^∗0
  xi xi 바리온
• 
  Ω⁻
  오메가 바리온

그러나, 이 십중구의 입자 중 하나는 8중 방법이 제안되었을 때 이전에 관찰된 적이 없었다.겔만은 이 입자를 δ라고 불렀고⁻
1962년 이상도 -3, 전하 -1, 질량은 1680 MeV/c에² 가까울 것이라고 예측했다.1964년 브룩헤이븐의 한 입자 가속기 그룹에 의해 이러한 예측과 거의 일치하는 입자가 발견되었다^[7].겔만은 소립자 이론을 연구한 공로로 1969년 노벨 물리학상을 받았다.

역사적 발전

발전

역사적으로 쿼크는 맛의 대칭에 대한 이해에 의해 동기부여가 되었다.우선, 입자 그룹이 SU(3)의 표현 이론과 일치하는 방식으로 서로 연관되어 있다는 것을 알아냈다.이로부터, 그룹 SU(3)에 의해서 파라메타화된 우주의 대략적인 대칭이 존재한다고 추측되었다.마지막으로(1964년) 이러한 SU(3) 변환에 의해 교환되는 세 개의 라이트 쿼크(위, 아래, 이상)가 발견되었다.

현대적 해석

8가지 방법은 현대의 용어로 다양한 종류의 쿼크 사이의 맛 대칭의 결과로 이해될 수 있다.강한 핵력은 맛에 관계없이 쿼크에 동일한 방식으로 영향을 미치기 때문에 하드론에서 한 가지 맛의 쿼크를 다른 맛의 쿼크로 교체해도 질량이 크게 변하지 않을 것이다. 단, 각각의 쿼크 질량이 세 가지 가벼운 쿼크에 대해 유지되는 강한 상호작용 척도보다 작다면 말이다.수학적으로 이 대체는 SU(3) 그룹의 요소로 설명할 수 있다.옥텟 및 기타 하드론 배열은 이 그룹을 나타냅니다.

플레이버 대칭

SU(3)

추상적인 3차원 벡터 공간이 있습니다.

$({displaystyle {text} {pmatrix} 1 \ 0 \ \ \ \ \ \ \ end { pmatrix } \ qu\ 、 \ qquad { pmatrix } 1 \ \ \ \ \ \ arar 、 \ arrow rowrow row row row row row {\ {\rowrow {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\$

그리고 물리 법칙은 결정식 1의 단일 변환을 이 공간에 적용하면 거의 불변한다(맛 회전이라고도 함).

${\displaystyle {begin{pmatrix}x\y\end{pmatrix}\map to A{\begin{pmatrix}x\y\z\end{pmatrix}},\quad {text{여기}}A는 }SU(3)에 있습니다.$

여기서 SU(3)는 결정식 1(특수 단위군)을 갖는 3×3 단위행렬의 Lie 군을 말한다.예를 들어 플레이버 로테이션은

$({displaystyle A=pmatrix}~\;~0&1&0\-1&0\\;~0&1\end{pmatrix})$

우주의 모든 업 쿼크를 다운 쿼크로 동시에 바꾸는 변환입니다.좀 더 구체적으로 말하자면, 이러한 맛의 회전은 강한 힘의 상호작용만 본다면 정확한 대칭이지만, 세 쿼크는 질량이 다르고 전자 약력의 상호작용이 다르기 때문에 우주의 정확한 대칭은 아닙니다.

이러한 대략적인 대칭을 향미 대칭, 또는 보다 구체적으로 향미 SU(3) 대칭이라고 합니다.

표현 이론과의 연관성

특정 입자($예$를 들어 $양성자$가 양자 상태에 있다고 가정합니다$.$입자에 향미 회전 A$중$ 하나를 적용하면 A라고$부를$ $수{\displaystyle }$ 있는 새로운 양자 상태가 됩니다.이$새로운$ 상태는 A에 따라서는 양성자 또는 중성자가 될 수 있습니다$.$양성자와 중성자의 중첩 또는 다양한 다른 가능성.가능한 모든 양자 상태의 집합은 벡터 공간에 걸쳐 있습니다.

표현 이론은 그룹의 요소(여기서 그룹 SU(3)의 향미 회전 A)가 벡터 공간의 자기동형인 상황을 설명하는 수학 이론입니다(여기서 향미 회전 양성자에서 얻을 수 있는 모든 가능한 양자 상태의 집합).따라서 SU(3)의 대표이론을 연구함으로써 벡터 공간이 무엇이며, 그것이 향미대칭에 의해 어떻게 영향을 받는지를 알 수 있다.

향미 회전 A는 정확한 대칭이 아니라 대략적인 대칭이기 때문에 벡터 공간의 각 직교 상태는 서로 다른 입자 종에 대응한다.위의 예에서 프로톤이 가능한 모든 플레이버 회전 A에 의해 변환되면 프로톤은 8차원 벡터 공간을 이동하는 것으로 밝혀졌다.이러한 8차원은 이른바 "바리온 옥텟"의 8개 입자(프로톤, 중성자, σ⁺
, σ^0
−
, ξ⁻
, ξ, λ⁰
)에 해당한다
.이는 그룹 SU(3)의 8차원("옥텟") 표현에 해당합니다.A는 대략적인 대칭이기 때문에, 이 옥텟의 모든 입자는 비슷한 ^[8]질량을 가지고 있다.

모든 Lie 그룹은 대응하는 Lie 대수를 가지며, Lie 그룹의 각 그룹 표현은 동일한 벡터 공간상의 대응하는 Lie 대수 표현에 매핑될 수 있다.$리$ ${\displaystyle \mathfrak{대수}}$는$$3×3 트레이스리스$에르미트$행렬의 집합으로 쓸 수 있다$.$$물리학자들$은 일반적으로 리 군 SU(3$)$ 대신 리 대수($)$의 표현 이론을 논의하는데, 이는 전자가 더 단순하고 두 가지가 궁극적으로 동일하기 때문이다.

메모들

레퍼런스

추가 정보

• M. Gell-Mann; Y. Ne'eman, eds. (1964). The Eightfold Way. W. A. Benjamin. LCCN 65013009. (8가지 방법에 대한 대부분의 역사 논문과 겔만-오쿠보 질량 공식을 포함한 관련 주제를 포함합니다.)