개미 군집 최적화 알고리즘

이 문서에는 여러 가지 문제가 있습니다.개선을 돕거나 토크 페이지에서 이러한 문제에 대해 논의해 주십시오.(이러한 템플릿메시지를 삭제하는 방법과 타이밍에 대해 설명합니다) 이 기사에는 독창적인 연구가 포함되어 있을 가능성이 있다. 클레임을 확인하고 인라인 인용을 추가하여 개선해 주십시오. 독창적인 연구로만 구성된 진술은 삭제되어야 한다.(2018년 8월) (이 템플릿메시지 삭제 방법 및 삭제 시기 확인) 이 문서에는 일반적인 참조 목록이 포함되어 있지만 대응하는 충분한 인라인 인용이 없습니다. 좀 더 정밀한 인용문을 도입하여 이 글의 개선에 도움을 주시기 바랍니다. (2018년 8월) (템플릿 메시지 삭제 방법 및 삭제 시기 확인) (이 템플릿메시지를 삭제하는 방법과 타이밍을 확인합니다)

컴퓨터 과학 및 운영 연구에서 개미 군락 최적화 알고리즘(ACO)은 그래프를 통해 좋은 경로를 찾는 것으로 축소될 수 있는 계산 문제를 해결하기 위한 확률론적 기술이다.인공 개미는 실제 개미의 행동에서 영감을 얻은 다중 에이전트 방법을 나타냅니다.생물학적 개미의 페로몬 기반 의사소통은 종종 사용되는 ^[2]지배적인 패러다임이다.인공 개미와 로컬 검색 알고리즘의 조합은 차량 라우팅 및 인터넷 라우팅과 같은 일종의 그래프를 포함하는 수많은 최적화 작업에 대한 선택 방법이 되었다.

예를 들어 개미 군락^[3] 최적화는 개미 ^[4]군락의 동작을 모델로 한 최적화 알고리즘의 한 종류입니다.인공 '개미'(예: 시뮬레이션 에이전트)는 가능한 모든 솔루션을 나타내는 매개변수 공간을 이동함으로써 최적의 솔루션을 찾는다.진짜 개미들은 페로몬을 눕혀서 그들의 환경을 탐험하면서 서로를 자원으로 인도합니다.시뮬레이션된 '개미'는 유사하게 자신의 위치와 솔루션의 품질을 기록하므로, 이후 시뮬레이션에서 더 많은 개미가 더 나은 ^[5]솔루션을 찾을 수 있다.이 접근법의 한 가지 변형은 벌 알고리즘으로, 또 다른 사회적 곤충인 꿀벌의 먹이찾기 패턴과 더 유사합니다.

이 알고리즘은 개미 군집 알고리즘 계열의 일종으로, 군집 인텔리전스 방식으로, 메타휴리스틱 최적화를 구성합니다.마르코 도리고가 1992년 박사학위 ^[6][7]논문에서 처음 제안한 첫 번째 알고리즘은 군집과 먹이 공급원 사이의 길을 찾는 개미들의 행동을 바탕으로 그래프에서 최적의 경로를 찾는 것을 목표로 했다.그 후, 보다 폭넓은 종류의 수치 문제를 해결하기 위해서 원래의 아이디어가 다양해졌고, 그 결과, 몇 가지 문제가 생겨나, 개미의 행동의 다양한 측면을 끌어내고 있다.넓은 관점에서 ACO는 모델 기반^[8] 검색을 수행하고 분포 알고리즘의 추정과 몇 가지 유사점을 공유합니다.

개요

자연계에서는 어떤 종의 개미가 무작위로 돌아다니다가 먹이를 발견하면 페로몬 자국을 깔고 군집으로 돌아간다.만약 다른 개미들이 그러한 길을 발견한다면, 그들은 무작위로 계속 이동하지 않고, 대신 길을 따라가고, 먹이를 찾게 되면 돌아와서 그것을 보강할 것이다.^[9]

그러나 시간이 흐르면서 페로몬 흔적이 증발하기 시작하고, 따라서 페로몬의 매력 강도가 감소합니다.개미가 길을 따라 이동했다가 다시 돌아오는 데 더 많은 시간이 걸릴수록 페로몬은 증발해야 한다.이에 비해 짧은 경로는 더 자주 이동하므로 긴 경로보다 짧은 경로에서 페로몬 밀도가 높아집니다.페로몬 증발은 국소적으로 최적의 용액으로의 수렴을 피할 수 있는 이점도 있다.만약 증발이 전혀 없다면, 첫 번째 개미들이 선택한 길은 다음 개미들에게 과도하게 끌리는 경향이 있을 것이다.이 경우, 솔루션 공간의 탐사는 제약될 것이다.실제 개미 시스템에서 페로몬 증발의 영향은 불분명하지만,^[10] 인공 시스템에서는 매우 중요합니다.

전체적인 결과는 한 개미가 군집에서 먹이 공급원으로 가는 좋은 (즉, 짧은) 길을 찾을 때, 다른 개미들은 그 길을 따라갈 가능성이 더 높으며, 긍정적인 피드백은 결국 많은 개미들이 하나의 길을 따르도록 이끈다.개미 군집 알고리즘의 아이디어는 풀어야 할 문제를 나타내는 그래프 주변을 걷는 "시뮬레이션 개미"로 이 행동을 모방하는 것입니다.

인텔리전트 객체의 주변 네트워크

"지능"은 더 이상 중앙 집중화되지 않고 모든 미세한 객체에서 찾을 수 있기 때문에 새로운 개념이 필요합니다.인간중심적 개념은 데이터 처리, 제어 유닛 및 계산력을 집중화하는 IT 시스템의 생산으로 이어지는 것으로 알려져 있습니다.이러한 중앙집중화된 장치는 지속적으로 성능을 증가시켜 왔고 인간의 뇌와 비교될 수 있다.뇌의 모델은 컴퓨터의 궁극적인 비전이 되었다.인텔리전트 오브젝트 및 나노 테크놀로지를 기반으로 한 신세대 정보 시스템의 주변 네트워크는 조만간 이 개념을 크게 변화시킬 것입니다.곤충에 비유할 수 있는 작은 장치들은 높은 지능을 스스로 폐기하지 않는다.사실, 그들의 지능은 상당히 제한적인 것으로 분류될 수 있다.예를 들어, 어떤 종류의 수학 문제를 푸는 능력을 가진 고성능 계산기를 인체에 이식하거나 상업용 물품을 추적하도록 설계된 지능형 태그에 통합하는 것은 불가능하다.하지만, 일단 이 물체들이 서로 연결되면, 개미나 벌의 군집과 비교할 수 있는 형태의 지능을 폐기한다.특정 문제의 경우, 이러한 유형의 지능은 ^[11]뇌와 유사한 중앙 집중식 시스템의 추론보다 우수할 수 있습니다.

자연은 만약 그들이 모두 같은 기본 규칙을 따른다면, 어떻게 아주 작은 유기체들이 거시적인 수준에서 집단 지능의 형태를 만들어 낼 수 있는지에 대한 몇 가지 예를 제공한다.사회성 곤충의 군집은 인간 사회와는 크게 다른 이 모델을 완벽하게 보여준다.이 모델은 단순하고 예측 불가능한 동작을 ^[12]가진 독립 유닛의 협력을 기반으로 합니다.그들은 특정 작업을 수행하기 위해 주변 영역을 이동하며, 그렇게 하기 위해 매우 제한된 양의 정보만을 소유합니다.예를 들어, 개미 군집은 주변 물체의 네트워크에도 적용될 수 있는 수많은 특성을 나타냅니다.개미 군집은 환경의 변화에 적응하는 능력이 매우 높을 뿐만 아니라 한 개인이 주어진 임무를 수행하지 못하는 상황에 대처하는 데 있어 엄청난 힘을 가지고 있다.이러한 유연성은 지속적으로 발전하는 객체의 모바일 네트워크에도 매우 유용합니다.컴퓨터에서 디지털 물체로 이동하는 정보의 소포는 개미와 같은 방식으로 행동한다.이들은 네트워크를 통해 이동하며 가능한 ^[13]한 빨리 최종 목적지에 도착하기 위해 하나의 노트에서 다음 노트로 이동합니다.

인공 페로몬계

페로몬 기반의 통신은 자연에서 널리 관찰되는 가장 효과적인 의사소통 방법 중 하나이다.페로몬은 벌, 개미, 흰개미와 같은 사회적 곤충에 의해 사용되며, 에이전트 간 및 에이전트 간 통신에 모두 사용됩니다.그 실현 가능성 때문에, 인공 페로몬은 다중 로봇과 무리 로봇 시스템에 채택되었다.페로몬 기반 통신은 화학적 또는 물리적(RFID 태그,^[17] 빛,^{[18][19][20][21]} 소리^[22])과 같은 다양한 방법으로 구현되었습니다.그러나 이러한 구현은 자연에서 볼 수 있는 페로몬의 모든 측면을 복제할 수 없었다.

투영된 빛을 사용하는 것은 Garnier, Simon 등의 2007년 IEEE 논문에서 마이크로 자율 ^[23]로봇과의 페로몬 기반 통신을 연구하기 위한 실험 설정으로 제시되었다.또 다른 연구는 로봇들이 움직이는 수평 LCD 화면을 통해 페로몬을 구현하고,^[24][25] 로봇들은 그 아래에 패턴을 등록하기 위해 아래쪽을 향한 광센서를 가지고 있는 시스템을 제시했다.

알고리즘 및 공식

개미 군체 최적화 알고리즘에서 인공 개미는 주어진 최적화 문제에 대한 좋은 해결책을 찾는 단순한 계산 에이전트입니다.개미 군집 알고리즘을 적용하기 위해서는 최적화 문제를 가중 그래프에서 최단 경로를 찾는 문제로 변환해야 합니다.각 반복의 첫 번째 단계에서, 각 개미는 확률적으로 해법을 구축한다. 즉, 그래프에서 가장자리가 따라야 하는 순서이다.두 번째 단계에서는 다른 개미들에 의해 발견된 경로를 비교합니다.마지막 단계는 각 가장자리의 페로몬 수준을 업데이트하는 것으로 구성됩니다.

프로시저 ACO_MetaHeuristic이 종료되지 않은 상태에서 generateSolutions() daemonActions() pheromoneUpdate() 반복 종료 프로시저

가장자리 선택

각각의 개미는 그래프를 통과하기 위한 해결책을 만들어야 한다.둘러보기의 다음 모서리를 선택하려면 개미는 현재 위치에서 사용 가능한 각 모서리의 길이와 해당 페로몬 수준을 고려합니다.알고리즘의 각 단계에서 각 개미는 $상태{\displaystyle }$x$(\$$displaystyle$x$$)에서 상태 y(\$displaystyle$y)로 이동하여 보다 완전한 중간 솔루션에 해당합니다.따라서 각 $개미{\displaystyle }$ k$\displaystyle$k는 각 반복에서 실현 가능한 확장의 ${\displaystyle {집합}_{}}$A k (${\displaystyle x}$)\$displaystyle A_{k}(x)$를 계산하여$$ 이들 중 하나로 이동합니다.$개미{\displaystyle }$k(\$displaystyle$ k$)$의 경우,$상태{\displaystyle }$ $x$(\$displaystyle$$x$$$)에서$$상태 ${\displaystyle {}_{}^{}}$(\$displaystyle$ y$$$)$로 이동할 ${\displaystyle {확률}_{}^{}}$은 두 값의 조합에 따라 ${\displaystyle {달라집니다}_{}}$.이동 매력은$$x $(\displaystyle$ \$eta _{$xy$$})입니다.이는 휴리스틱에 의해 계산됩니다.그는 그 이동의 우선순위 및 이동의 추적 $수준{\displaystyle {}_{}}$ ${\displaystyle y_{}}$x y \ $displaystyle$ \$display$ _ ${xy}$을(를) 사용하여 특정 이동을 수행하는 것이 과거에 얼마나 능숙했는지를 나타냅니다.추적 수준은 이동의 바람직성에 대한 사후적 징후를 나타냅니다.

$일반적$으로$k번째$$$개미는$x상태$에서$y상태$로 이동합니다.

$({displaystyle p_{xy}^{\alpha})(\eta _{xy}^{\alpha}) {\sum _{z\in \mathrm {allowed} _{x}(\alpha})(\eta _{xz}^{\alpha}}})$

$여기$서 ${\displaystyle x_{}}$ ${\displaystyle x_{}}$ y$$\ $displaystyle$\ $display$ $style$_ { $xy$}는 상태$$$x$에서$y{\displaystyle }$ \ $displaystyle$$$y로 이행하기 위해 퇴적된 페로몬의 양입니다. ${\displaystyle 0_{}}$ $\alpha {\displaystyle }$α \ $displaystyle$$\$ $\}$ {\ , y y y y y y y$y$ y y y y y y y y y y y y y y y y y y y where where where where where y y y y y y y y y y y y y {\ {\ {\ {\ {\ {\ y y {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\상태 $전이{\displaystyle }$ $xy($$일반적$으로${\displaystyle }$1/${\displaystyle d_{}}$ $($1/$d_{xy$ 여기서$d{\displaystyle }$$${$displaystyle$ d}는 거리$$) 및 β(\$displaystyle$$$\displaystyle \$eta$ _${xy$ $$$1{\displaystyle }$ 1은$x{\displaystyle {}_{}}$$$${\displaystyle {\mathrm{xy}}_{}}$의 영향을 제어하는 $파라미터$입니다.$playstyle \displaystyle$ _${xz}$ 및$$ ${\displaystyle x_{}}$ ${\displaystyle x_{}}$z \$displaystyle \eta$ _${xz}$는 다른 가능한 상태 천이에 대한 추적 수준과 매력을 나타냅니다.

페로몬 업데이트

트레일은 보통 모든 개미가 해결책을 완료했을 때 갱신되며, 각각 "좋은" 또는 "나쁜" 해결책의 일부였던 움직임에 대응하는 트레일의 수준을 높이거나 낮춥니다.글로벌 페로몬 업데이트 규칙의 예는 다음과 같습니다.

$\displaystyle \tau _{xy}\left 화살표 (1-\rho)\tau _{xy}+\sum _{k}{m}\Delta \tau _{xy}^{k}$

여기서 ${\displaystyle x_{}}$ x$$ ( \ $displaystyle$ \ $tau _${ $xy$ } ) 、 ${\$ \ $displaystyle$${\displaystyle \mathrm{xy}}$、 （ \ displaystyle \ $rho ）$는 페로몬 증발 계수, $($ \ $displaystyle$ m$$）은$$ 개미 수, $\delta {\displaystyle \mathrm{}}$ ${\displaystyle {\tau }_{}^{}}$ $($ \ $displaystyle$\$Delta$\$tau$ ）는 {$$ky $}$의 $양$입니다$.$$k번째$$$개미에 $의해{\displaystyle }$ 퇴적된 페로몬$($일반적으로 TSP 문제(그래프의 호에 대응하는 움직임)에 의해 주어짐)

${\displaystyle \Delta \delta _{xy}^{k}={begin{case}Q/L_{k}&{\mbox{개미}}}kymbox{tour}\0&{\mbox{cases}}}\mbox{cases}}}$

${\displaystyle {여기}_{}}$서 L k$(\$$displaystyle$ $L_{k$})는$$ k$(일반적$으로 길이) $개미$ 투어 $비용$이고$$Q(\$displaystyle$ Q$)$는 상수입니다.

공통 내선번호

다음은 ACO 알고리즘의 가장 일반적인 변형입니다.

개미 시스템(AS)

개미 시스템은 최초의 ACO 알고리즘입니다.이 알고리즘은 위의 알고리즘에 대응합니다.그것은 ^[26]도리고에 의해 개발되었다.

개미 군집 시스템(ACS)

개미 군체 시스템 알고리즘에서는 원래 개미 시스템이 세 가지 측면에서 수정되었습니다.

1. 에지 선택은 이용에 치우친다(즉, 페로몬 양이 많은 최단 에지 선택 가능성 선호).
2. 솔루션을 구축하는 동안 개미는 로컬 페로몬 업데이트 규칙을 적용하여 선택한 에지의 페로몬 수준을 변경합니다.
3. 각 반복의 마지막에 변경된 글로벌페로몬 갱신 ^[27]규칙을 적용하여 최적의 개미만 추적을 갱신할 수 있습니다.

엘리트 개미계

이 알고리즘에서 글로벌 최적 솔루션은 모든 다른 개미와 함께 모든 반복 후에(이 흔적을 다시 찾지 않았더라도) 페로몬을 추적에 저장합니다.엘리트 전략은 현재 최선의 경로의 링크를 포함하는 솔루션을 구축하기 위해 모든 개미를 탐색하도록 지시하는 것을 목표로 한다.

최대 최소 개미 시스템(MMAS)

이 알고리즘은 각 트레일의 최대 및 최소 페로몬 양을 제어합니다.페로몬을 트레일에 추가할 수 있는 것은 글로벌베스트 투어 또는 반복베스트 투어뿐입니다검색 알고리즘의 정체를 피하기 위해 각 트레일에서 가능한 페로몬 양의 범위는 간격 [,,,]로_maxmin 제한됩니다.모든 엣지가 θ로_max 초기화되어 보다 높은 솔루션 탐사를 강제합니다.정체기에 ^[28]가까워지면 트레일은 when로_max 재초기화된다.

랭크 기반 개미 시스템(ASrank)

모든 솔루션은 길이에 따라 순위가 매겨집니다.이 반복에서 가장 우수한 개미 중 고정된 수만큼만 평가판을 업데이트할 수 있습니다.퇴적된 페로몬의 양은 각 용액에 가중치를 부여하여 경로가 짧은 용액이 경로가 긴 용액보다 더 많은 페로몬을 퇴적시킨다.

연속직교개미군락지(COAC)

COAC의 페로몬 퇴적 메커니즘은 개미들이 협력적이고 효과적으로 해결책을 찾을 수 있도록 하는 것이다.직교 설계 방법을 사용하여 실현 가능한 영역의 개미는 글로벌 검색 능력과 정확성을 향상시키면서 선택한 영역을 빠르고 효율적으로 탐색할 수 있다.직교 설계 방법과 적응 반지름 조정 방법은 실제 ^[29]문제를 해결하는 데 있어 더 넓은 이점을 제공하기 위해 다른 최적화 알고리즘으로도 확장할 수 있습니다.

재귀 개미 군락 최적화

이것은 전체 검색 도메인을 여러 하위 도메인으로 나누고 이러한 하위 ^[30]도메인에 대한 목표를 해결하는 개미 시스템의 재귀적 형태입니다.모든 서브도메인의 결과를 비교하고 그 중 가장 소수의 서브도메인이 다음 레벨로 승격됩니다.선택한 결과에 해당하는 하위 도메인이 더 세분화되고 원하는 정밀도의 출력이 얻어질 때까지 프로세스가 반복됩니다.이 방법은 잘못된 지구물리학적 반전 문제에 대해 테스트되었으며 잘 ^[31]작동합니다.

컨버전스

알고리즘의 일부 버전에서는 컨버전스임을 증명할 수 있습니다(즉, 한정된 시간 내에 글로벌 최적화를 찾을 수 있습니다).개미 군집 알고리즘의 수렴 증거는 2000년에 최초로 작성되었으며, 이후 ACS 및 MMAS 알고리즘에 대한 그래프 기반 개미 시스템 알고리즘이다.대부분의 메타휴리스틱과 마찬가지로 이론적으로 수렴 속도를 추정하는 것은 매우 어렵다.다양한 파라미터(엣지 선택 전략, 거리 측정 메트릭 및 페로몬 증발률)에 대한 연속 개미 군집 알고리즘의 성능 분석 결과, 그 성능과 수렴 속도는 선택된 파라미터 값, 특히 페로몬 증발률 ^[32]값에 민감하게 반응하는 것으로 나타났다.2004년에 즐친과 그의 동료들은^[33] COAC 유형 알고리즘이 분포 알고리즘의 교차 엔트로피와 추정에 확률적 경사 강하 방법을 동화시킬 수 있다는 것을 보여주었다.그들은 이러한 메타휴리스틱스를 "연구 기반 모델"로 제안했다.

적용들

개미 군집 최적화 알고리즘은 2차 할당에서 단백질 폴딩 또는 라우팅 차량에 이르기까지 많은 조합 최적화 문제에 적용되었으며, 많은 파생 방법들이 실제 변수, 확률적 문제, 다중 표적 및 병렬 구현의 동적 문제에 적용되었다.또한 출장 세일즈맨 문제에 대한 최적의 해결책을 도출하는 데도 사용되고 있습니다.그래프가 동적으로 변경될 수 있는 경우 유사한 문제의 시뮬레이션 어닐링 및 유전 알고리즘 접근법보다 유리합니다. 개미 군집 알고리즘은 지속적으로 실행되며 실시간으로 변화에 적응할 수 있습니다.이는 네트워크 라우팅 및 도시 교통 시스템에 관심이 있습니다.

첫 번째 ACO 알고리즘은 개미^[26] 시스템이라고 불리며 일련의 도시를 연결하는 가장 짧은 왕복 여행을 찾는 것이 목표인 여행 세일즈맨 문제를 해결하기 위한 것이었다.일반적인 알고리즘은 비교적 단순하며, 각각 도시를 따라 가능한 라운드 트립 중 하나를 만드는 개미 집합을 기반으로 합니다.각 단계에서 개미는 몇 가지 규칙에 따라 한 도시에서 다른 도시로 이동하는 것을 선택한다.

1. 각 도시를 정확히 한 번 방문해야 합니다.
2. 멀리 있는 도시는 선택될 가능성이 적다.
3. 페로몬 트레일이 두 도시 사이의 가장자리에 펼쳐질수록 그 가장자리가 선택될 확률이 높아집니다.
4. 여정을 마친 개미는 여정이 짧으면 횡단한 모든 모서리에 페로몬을 더 많이 묻힌다.
5. 반복할 때마다 페로몬의 흔적이 증발합니다.

스케줄링 문제

• 시퀀셜 오더 문제(SOP)
• Job-shop 스케줄링 문제(JSP)^[35]
• 오픈샵 스케줄링 문제(OSP)^[36][37]
• 치환 플로우샵 문제(PFSP)^[38]
• 단일 시스템 총 지연 문제(SMTTP)^[39]
• 단일 머신 총 가중 지연 문제(SMTWTP)^[40][41][42]
• 자원 제약 프로젝트 스케줄링 문제(RCPSP)^[43]
• 그룹샵 스케줄링 문제(GSP)^[44] 문제(Group-Shop Scheduling)
• 시퀀스에 의존한 셋업 시간(SMTTPDST)^[45]에 의한 단일 머신의 합계 지연 문제
• 시퀀스에 따라 설정/전환^[46] 시간이 달라지는 Multistage Flowshop Scheduling Problem(MFSP; 다단계 플로우샵 스케줄링 문제)
• Assembly Sequence Planning(ASP; 어셈블리시퀀스 플래닝) 문제^[47]

차량 배선 문제

• 캐패시티브 차량 라우팅 문제(CVRP)^[48][49][50]
• 다중 저장소 차량 라우팅 문제(MDVRP)^[51]
• Period Vehicle Routing Problem(PVRP;^[52] 기간 차량 라우팅 문제)
• 분할 배송 차량 라우팅 문제(SDVRP)^[53]
• 확률적 차량 라우팅 문제(SVRP)^[54]
• 픽업 및 배송(VRPPD)^[55][56]과 관련된 차량 라우팅 문제
• 시간 창(VRPTW)^{[57][58][59][60]}과 관련된 차량 라우팅 문제
• 시간대별 차량 라우팅 문제(TDVRPTW)^[61]
• 시간 창 및 다중 서비스 작업자(VRPTWMS)와 관련된 차량 라우팅 문제

할당 문제

• 2차 할당 문제(QAP)^[62]
• Generalized Assignment Problem(GAP;^[63][64] 일반 할당 문제)
• 주파수 할당 문제(FAP)^[65]
• 용장 할당 문제(RAP)^[66]

문제 설정

• Set cover 문제(SCP)^[67][68]
• 파티션 문제(SPP)^[69]
• 가중치 제약 그래프 트리 파티션 문제(WCGTP)^[70]
• Arc-weighted l-cardinality tree 문제(AWLCTP)^[71]
• 다중 배낭 문제(MKP)^[72]
• Maximum Independent Set 문제(MIS; ^[73]최대 독립 집합 문제)

나노일렉트로닉스 물리 설계에서의 디바이스 크기 문제

• 45 nm CMOS 기반의 센스 앰프 회로의 개미 군집 최적화(ACO) 기반 최적화는 매우 짧은 ^[74]시간에 최적의 솔루션으로 수렴할 수 있습니다.
• 개미 군락 최적화(ACO) 기반의 가역 회로 합성은 효율을 크게 ^[75]향상시킬 수 있습니다.

안테나 최적화 및 합성

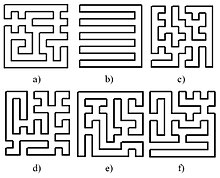
안테나의 형태를 최적화하기 위해 개미 군집 알고리즘을 사용할 수 있습니다.예를 들어 안테나 RFID 태그는 개미 군집 알고리즘(^[77]ACO), 루프백 및 언루프백 진동자 10×10을^[76] 기반으로 합니다.

이미지 처리

ACO 알고리즘은 영상 에지 감지 및 에지 ^[78][79]링크를 위한 영상 처리에 사용됩니다.

• 에지 감지:

이 그래프는 2차원 이미지입니다개미들은 페로몬을 축적하는 하나의 픽셀을 통과합니다한 픽셀에서 다른 픽셀로 개미의 움직임은 영상의 강도 값의 국소적인 변화에 의해 결정됩니다.이 움직임으로 인해 페로몬의 밀도가 가장 높은 가장자리가 퇴적됩니다.

ACO 를 사용한 ^[80][81][82]엣지 검출의 순서는 다음과 같습니다.

순서 1: 초기화.$이미지{\displaystyle {}_{}}$ ${\displaystyle {I{}_{}}_{}}$ ${\displaystyle {{}_{}{}_{}}_{}}$ ${\displaystyle {{M2}_{}}_{}}$에$$K$({$$displaystyle K}$개미를$$$$ 랜덤으로 $배치$합니다.$여기$서 K $=$ ( ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {M2\mathrm{}}_{}{}^{}}$ ${\displaystyle {\frac{1}{}}^{}}$2 ($M_{1}*M_{2})^{\tfrac${2}} $매트릭스.$초기화 프로세스의 주요 과제는 휴리스틱 매트릭스를 결정하는 것입니다.

휴리스틱 행렬을 결정하는 방법은 다양합니다.다음 예에서는 휴리스틱 매트릭스가 로컬 통계(픽셀 위치$({\displaystyle }$ ${\displaystyle i}$,${\displaystyle j}$ )$$\$displaystyle (i , j$ )$$} )에 근거해 계산되었습니다.

$\displaystyle \eta _{(i,j)}=tfrac {1}{Z}}*Vc*I_{(i,j)}}$

$여기$서$$I(\$displaystyle$ I$)$는 ${\displaystyle {M1\mathrm{}}_{}{}_{}}$ $(\$의 이미지입니다.

${\displaystyle Z=\sum _{i=1:M_{1}}\sum _{j=1:M_{2}}: Vc(I_{i,j})}$

정규화 요인입니다.

${\displaystyle {begin{i,j}=&f\left(\left\vert I_{(i-2,j-1)}-I_{(i+2,j+1)}-Right\vert I_{(i-2,j+1)}-I_{(i+j-1)}\\+\left\vert I_{(i-1,j-2)}-I_{(i+1,j+2)}-I_{(i-1,j-1)}-I_{(i+1,j+1)}-오른쪽\vert \+\vert I_{j-1},i}-{j-1}-I_{i}-{(i}-right\+vert\left\,j+\vert,j-1)}\left\vert I_{(i-1,j+2)}-I_{(i-1,j-2)}\right\vert +\left\vert I_{(i,j-1)}-I_{(i,j+1)}\right\vert \end{aligned}}$

${\displaystyle f}$( ${\displaystyle )}$ )$${ $displaystyle$ f ( \ $cdot$) }는$$ 다음 함수를 사용하여 계산할 수 있습니다.

$\displaystyle f(x)=\displayda x,\display {x 0 0; (1)}$

${\displaystyle f(x)=\displayda x^{2},\display {x ≥ 0; (2)}}$

$\displaystyle f(x)=cases\frac {pi x}{2\facedda },\text {cases},\text {cases},\text {cases},\text {cases},\text {cases}$

$\displaystyle f(x)=pi x\sinfac\frac {pi x} {2\casesda },\text {\text {\cases},\text {\cases},\text {\cases}$

위의 각 기능에서 파라미터 ${\(\displaystyle \lambda)$에 의해 각 기능의 모양이 조정됩니다.

2단계: 구축 프로세스개미의 움직임은 4개의 연결된 픽셀 또는 8개의 연결된 픽셀을 기반으로 합니다.개미가 움직일 확률은 $확률식{\displaystyle {}_{}}$ ${\displaystyle P_{}}$x ,$$ \ $displaystyle P_{x$, $y}$에 의해 주어진다.

스텝 3 및 스텝5: 갱신 프로세스페로몬 매트릭스가 두 번 업데이트됩니다.3단계에서는 개미의 흔적(${\displaystyle {}_{}}$( (${\displaystyle x_{}}$,${\displaystyle y_{}}$ $)$ {$displaystyle \displaystyle$ _${(x,y)}})$이 업데이트되고, 5단계에서는 다음과 같이 흔적 증발률이 업데이트됩니다.

${\displaystyle e_{}}$n e ${\displaystyle \mathrm{w}\leftarrow }$ ( 1 -${\displaystyle {}_{}}$ ) ${\displaystyle o_{}d}$ +$$ 0 \$displaystyle$ \ $_rowrow$ （ \ displaystyle \$new$} \$ar1$ ($1$ - \$psi$ ) \$_$ _$${ 0 }$$,

$여기$서 $"\displaystyle \psi"$는 페로몬 붕괴 0 < < \$displaystyle$ 0 $<\$ displaystyle < $1$} 입니다.

스텝 7: 의사결정 프로세스K개미가 N회 반복을 위해 고정 거리 L을 이동하면, 그것이 엣지인지 아닌지는 페로몬 행렬의 임계값 T에 근거해 판단됩니다.아래 예의 임계값은 Otsu의 방법에 따라 계산됩니다.

ACO를 사용하여 이미지 가장자리가 감지됨:아래 이미지는 (1)부터 (4)^[83]까지의 식에 따라 다른 함수를 사용하여 생성됩니다.

• 엣지 ^[84]링크: ACO는 엣지 링크 알고리즘에서도 유효하다는 것이 증명되었습니다.

기타 응용 프로그램

• 파산예측^[85]
• 분류^[86]
• 커넥션 지향 네트워크^[87] 라우팅
• 커넥션리스 네트워크^[88][89] 라우팅
• 데이터 마이닝^{[86][90][91][92]}
• 프로젝트 일정에서^[93] 할인된 현금 흐름
• 분산 정보 검색^[94][95]
• 에너지 및 전력 네트워크^[96] 설계
• 그리드 워크플로우 스케줄링^[97] 문제
• 단백질 상호작용을^[98] 위한 억제성 펩타이드 설계
• 인텔리전트 테스트^[99] 시스템
• 전력 전자 회로^[100] 설계
• 단백질 폴딩^{[101][102][103]}
• 시스템 식별^[104][105]

정의의 어려움

ACO 알고리즘에서는 그래프 내의 2개의 포인트A와 B 사이의 최단 패스는 여러 ^[106]패스의 조합으로 구축됩니다.알고리즘이 개미 군집인지 아닌지에 대한 정확한 정의를 내리는 것은 쉽지 않다. 왜냐하면 그 정의는 저자와 용도에 따라 다를 수 있기 때문이다.일반적으로 개미 군집 알고리즘은 탐색 ^[107]공간에서 움직이는 개미로 대표되는 각각의 해로 구성된 메타휴리스틱으로 간주된다.개미는 최선의 해결책을 표시하고 이전의 표시를 고려하여 검색을 최적화합니다.각 반복 ^[108]간의 전환을 위해 확률 분포를 사용하는 확률론적 다중 작용 알고리즘으로 볼 수 있다.조합 문제에 대한 버전에서는 ^[109]반복적인 솔루션 구성을 사용합니다.일부 저자에 따르면 ACO 알고리즘을 다른 친척과 구별하는 것(분포나 입자 군집 최적화를 추정하는 알고리즘 등)은 정확히 건설적인 측면이다.조합 문제에서, 어떤 개미도 효과가 없을지라도, 결국 가장 좋은 해결책을 찾을 수 있다.따라서 Traveling sales 문제의 예에서는 개미가 최단 경로를 이동할 필요가 없습니다.최단 경로는 최단 솔루션의 가장 강력한 세그먼트에서 구축할 수 있습니다.그러나 이 정의는 '근린' 구조가 존재하지 않는 실제 변수의 문제의 경우 문제가 될 수 있다.사회적 곤충들의 집단 행동은 연구원들에게 영감을 주는 원천으로 남아 있다.생물 시스템에서 자기 조직화를 추구하는 다양한 알고리즘(최적화 여부를 불문하고)은 개미 군집 알고리즘이 들어맞는 매우 일반적인 프레임워크인 "스팜 인텔리전스"^[11]의 개념을 이끌어냈다.

스티그너지 알고리즘

실제로는 "개미 군락"이라고 주장하는 알고리즘이 다수 존재하지만, 표준 개미 ^[110]군락의 최적화에 관한 일반적인 프레임워크는 항상 공유하지 않는다.실제로, 환경을 통한 개미들 간의 정보 교환의 사용은 알고리즘이 개미 군집 알고리즘의 종류에 속하기에 충분한 것으로 여겨진다.이 원리로 인해 일부 저자들은 먹이 찾기, 애벌레 선별, 분업 및 협력 ^[111]운송에 기초한 방법과 행동을 정리하기 위해 "가치"라는 용어를 만들었다.

관련 방법

유전자 알고리즘(GA)

이러한 솔루션은 하나의 솔루션이 아니라 하나의 솔루션 풀을 유지합니다.뛰어난 솔루션을 찾는 프로세스는 솔루션의 풀을 변경하기 위해 결합 또는 변형되고 품질이 낮은 솔루션은 폐기되는 등 진화의 과정을 모방합니다.

분포 알고리즘(EDA) 추정

기존 재현 연산자를 모델 유도 연산자로 대체하는 진화 알고리즘입니다.그러한 모델은 기계 학습 기술을 사용하여 모집단에서 학습되며, 확률론적 그래픽 모델로 표현되며, 여기에서 새로운 솔루션을 추출하거나^[112][113] 교차 ^[114][115]유도에서 생성할 수 있다.

시뮬레이트 어닐링(SA)

현재 솔루션의 인접 솔루션을 생성하여 서치 공간을 횡단하는 관련 글로벌 최적화 기술입니다.상위 네이버는 항상 허용됩니다.품질 차이와 온도 파라미터에 근거하여 확률적으로 열등한 인접 라우터를 받아들인다.온도 파라미터는 알고리즘이 진행됨에 따라 변경되어 검색의 특성이 변경됩니다.

사후 대응 검색 최적화

내부 피드백 루프를 추가하여 문제, 인스턴스 및 현재 솔루션 주변의 로컬 상황에 대한 알고리즘의 자유 매개 변수를 자체 조정함으로써 기계 학습과 최적화를 결합하는 데 초점을 맞춥니다.

Tabu 검색(TS)

두 가지 모두 개별 용액의 돌연변이를 테스트하여 솔루션 공간을 이동하는 시뮬레이션 어닐링과 유사합니다.시뮬레이트된 어닐링에서는 하나의 변환 솔루션만 생성되지만 tabu 검색에서는 다수의 변환 솔루션이 생성되어 생성된 솔루션 중 가장 적합성이 낮은 솔루션으로 이동합니다.솔루션 공간의 순환을 방지하고 이동을 촉진하기 위해 부분 솔루션 또는 전체 솔루션 목록을 유지합니다.솔루션이 솔루션 공간을 통과할 때 업데이트되는 tabu 목록의 요소를 포함하는 솔루션으로 이동하는 것은 금지됩니다.

인공면역시스템(AIS)

척추동물의 면역체계를 본떠 만든거죠

입자 군집 최적화(PSO)

군집 지능화 방법.

인텔리전트 워터 드롭(IWD)

하천을 흐르는 자연 물방울을 기반으로 한 군집 기반 최적화 알고리즘

중력 탐색 알고리즘(GSA)

군집 지능화 방법.

개미 군집 클러스터링 방법(ACCM)

ACO를 확장하는 클러스터링 방식을 사용하는 방식입니다.

확률확산검색(SDS)

목적 함수를 여러 개의 독립적인 부분 함수로 분해할 수 있는 문제에 가장 적합한 에이전트 기반 확률론적 전역 검색 및 최적화 기법.

역사

개미 군락 최적화 알고리즘의 연표.

• 1959년, Pierre-Paul Grassé는 ^[116]흰개미 둥지 건설의 행동을 설명하기 위해 Stigmergy 이론을 발명했다.
• 1983년 드뇌부르와 그의 동료들은 ^[117]개미의 집단 행동을 연구했다.
• 1988년, 그리고 Moyson Manderick은 ^[118]개미들 사이의 자기 조직화에 관한 기사를 가지고 있다.
• 1989년 아르헨티나 개미의 집단행동에 대한 Goss, Aron, Dneubourg 및 Pastels의 연구로 개미 군집 최적화 ^[119]알고리즘의 아이디어가 제시되었다.
• 1989년, Ebling과 그의 ^[120]동료들에 의한 식품에 대한 행동 모델 구현
• 1991년 M. Dorigo는 박사학위 논문(1992년 발표^[7])에서 개미계를 제안했다.논문에서 발췌하여 V가 공동 집필한 기술 보고서입니다.마니에조와 A.콜로니는^[121] 5년 후에 출판되었다.^[26]
• 1994년, Appleby와 British Telecommunications Plc의 스튜어드는 통신 네트워크에^[122] 대한 최초의 애플리케이션을 발표했습니다.
• 1995년 Gambardella와 Dorigo는 개미 시스템의 첫 번째 이점으로 개미 군집 시스템의 ^[123]예비 버전인 개미-q를 제안했다.^[26]
• 1996년, 감바르델라와 도리고는 개미 군체제를 제안했다.
• 1996년 개미 체계에 ^[26]관한 기사 발표
• 2000년 Hoos와 Stützle은 max-min 개미 시스템을 ^[28]발명했다.
• 1997년 Dorigo와 Gambardella는 지역 ^[27]탐색과 교배된 개미 군집 시스템을 제안했다.
• 1997년, Schoonderwoerd와 그의 동료들은 통신 ^[125]네트워크에 개선된 애플리케이션을 발표했습니다.
• 1998년, Dorigo는 ACO ^[126]알고리즘에 관한 최초의 컨퍼런스를 개시.
• 1998년 Stützle은 초기 병렬 ^[127]구현을 제안한다.
• 1999년, Gambardella, Taillard 및 Agazi는 macs-vrptw를 제안했습니다.이것은 시간창이 ^[57]있는 차량 경로 문제에 적용되는 최초의 다중 개미 군체 시스템입니다.
• 1999년 보나보, 도리고, 테라울라즈는 주로^[128] 인공개미를 다룬 책을 출판했다.
• 개미 알고리즘에^[129] 관한 Future Generation Computer Systems 저널 2000년호
• 2000년, 스케줄링, 스케줄링 순서 및 제약 조건의 충족에 대한 첫 번째 적용
• 2000년, Gutjahr은 개미^[130] 군집의 알고리즘에 대한 수렴의 첫 증거를 제공한다.
• 2001년, 기업(Eurobios 및 AntOptima)에 의한 COA 알고리즘의 최초 사용.
• 2001년 Iredi와 그의 동료들은 최초의 다목적 알고리즘을^[131] 발표했다.
• 2002년, 일정 설계의 첫 번째 응용 프로그램, 베이지안 네트워크
• 2002년, Biancchi와 그녀의 동료들은 확률적 문제에 ^[132]대한 첫 번째 알고리즘을 제안했다.
• 2004년 Dorigo와 Stützle은 MIT Press와 함께 개미 군락 최적화 책을 출판합니다.
• 2004년 Zlochin과 Dorigo는 일부 알고리즘이 확률적 경사 강하, 교차 엔트로피 방법 및 분포를 추정하기^[33] 위한 알고리즘과 동등함을 보여준다.
• 2005년, 단백질 접힘 문제에 대한 첫 번째 적용.
• 2012년, Prabhakar와 동료들은 컴퓨터 네트워크 구성 원리를 반영하여 페로몬 없이 동시에 통신하는 개미의 작동에 관한 연구를 발표했습니다.통신 모델은 전송 제어 ^[134]프로토콜과 비교되었습니다.
• 2016년, 펩타이드 배열 ^[98]설계에 첫 적용.
• 2017년, ACO 알고리즘(HUMANT 알고리즘)^[135]에 다중 기준 의사결정 방법 PROMETHEE를 성공적으로 통합.

레퍼런스

출판물(선택)

• M. 도리고, 1992년최적화, 학습 및 자연 알고리즘, 이탈리아, Politecnico di Milano 박사 논문.
• M. Dorigo, V. Maniezo & A.콜로니, 1996년"개미 시스템: 협력 에이전트의 콜로니에 의한 최적화", 시스템, 인간 및 사이버네틱스의 IEEE 트랜잭션– Part B, 26 (1) : 29 ~41 。
• M. Dorigo & L. M. Gambardella, 1997년"개미 군체 시스템: 출장 세일즈맨 문제에 대한 공동 학습 접근법.진화적 계산에 관한 IEEE 트랜잭션, 1: 53~66.
• M. Dorigo, G. Di Caro & L. M. Gambardella, 1999.이산 최적화를 위한 개미 알고리즘.인공생명체, 5(2): 137~172.
• E. 보나보, M. 도리고 외 G.테라울라즈, 1999년군집 인텔리전스: 옥스포드 대학 출판부, 내추럴에서 인조 시스템까지.ISBN 0-19-513159-2
• M. Dorigo & T. Stützle, 2004.개미 군락 최적화, MIT 프레스.ISBN 0-262-04219-3
• M. Dorigo, 2007."개미 군체 최적화"스콜라피디아.
• C. Blum, 2005 "개미 군체 최적화: 소개 및 최신 동향"생명체의 물리학 리뷰, 2: 353-373
• M. Dorigo, M. Birattari & T. Stützle, 2006 개미 군체 최적화: 컴퓨터 인텔리전스 기술로서의 인공 개미.TR/IRIDIA/2006-023
• Mohd Murtadha Mohamad, "사료개미 전략을 이용한 인공 로봇 모션 계획", 정보기술 저널, Vol.20, No. 163-181, ISSN 0128-3790, 2008년 12월.
• N. Monmarché, F. Guinand & P. Siarry(에드), "인공 개미", 2010년 8월 하드백 576 페이지.ISBN 978-1-84821-194-0.
• A. Kazharov, V. Kureichik, 2010."수송 문제를 해결하기 위한 개미 군체 최적화 알고리즘", 컴퓨터 및 시스템 과학 저널, 제49권.No. 1. 페이지 30-43
• C-M. Pintea, 2014, 조합 최적화 문제를 위한 바이오 인스파이어 컴퓨팅의 진보, Springer ISBN 978-3-642-40178-7
• K. 살렘, 노스 피살, M. A. 바하루딘, A. A.Ahmed, S. Hafizah 및 S. Kamilah, "개미 군락은 무선 센서 네트워크를 위한 크로스 레이어 아키텍처를 기반으로 자체 최적화된 라우팅 프로토콜에 영감을 주었습니다.", WSEAS Trans.Communic., 제9권, 제10호, 669~678페이지, 2010.ISBN 978-960-474-200-4
• K. 살렘과 N.Fisal, "무선 센서 네트워크에서의 자체 최적화 데이터 확실한 루팅을 위한 강화된 개미 군체 알고리즘", 네트워크 (ICON) 2012 제18회 IEEE 국제회의, 페이지 422–427.ISBN 978-1-4673-4523-1
• 루드포슈티 FR, 아볼마알리 S개미 군락법을 사용한 포트폴리오 최적화 테헤란 증권거래소의 도입 사례.회계 저널2018년 3월 8일 (1)

외부 링크

• Scholarpedia 개미 군락 최적화 페이지
• 개미 군락 최적화 홈페이지
• "개미 군체 최적화" - 러시아 과학 및 연구 커뮤니티
• AntSim - 개미 군집 알고리즘 시뮬레이션
• 개미 군락 최적화에 기반한 MIDACO-Solver 범용 최적화 소프트웨어(Matlab, Excel, VBA, C/C++, R, C#, Java, Fortran 및 Python)
• 독일 카이저슬라우테른 대학, AG Wehn: 개미 시스템으로 해결된 여행 세일즈맨의 개미 군체 최적화 애플릿 다양한 옵션과 파라미터(Java 애플릿)
• 개미농장 시뮬레이터
• 개미 알고리즘 시뮬레이션(Java 애플릿)
• 자바 개미 군락 시스템 프레임워크