3D 재구성

3D reconstruction
의료 영상의 3D 재구성은 반복 재구성을 참조하십시오.음원의 3D 재구성은 3D 사운드 재구성을 참조하십시오.
작은 해양 민달팽이 Pseudunela viatoris의 오른쪽 측면도 일반 해부도를 3D로 재구성했습니다.

컴퓨터 비전과 컴퓨터 그래픽스에서 3D 재구성은 실제 물체의 모양과 외관을 포착하는 과정입니다.이 프로세스는 액티브 또는 패시브 방식으로 실행할 [1]수 있습니다.모형이 시간 내에 모양을 변경할 수 있는 경우 이를 비강성 또는 시공간 [2]재구성이라고 합니다.

동기 부여 및 응용 프로그램

3D 재구성의 연구는 항상 어려운 목표였습니다.3D 재구성을 사용하면 모든 객체의 3D 프로파일을 결정할 수 있을 뿐만 아니라 프로파일 상의 모든 점의 3D 좌표를 알 수 있습니다.객체의 3D 재구성은 일반적으로 과학적인 문제이며 CAGD(Computer Aided Geometry Design), 컴퓨터 그래픽스, 컴퓨터 애니메이션, 컴퓨터 비전, 의료 이미징, 컴퓨터 과학, 가상 현실, 디지털 미디어 [3]등 다양한 분야의 핵심 기술입니다.예를 들어, 환자의 병변 정보를 컴퓨터에 3D로 표시할 수 있어 새롭고 정확한 진단 방법을 제공하므로 중요한 임상적 [4]가치가 있습니다.디지털 고도 모델은 공중 레이저 고도[5] 측정 또는 합성 개구 [6]레이더와 같은 방법을 사용하여 재구성할 수 있습니다.

액티브 메서드

수중 협곡의 3D 에코 사운딩 맵

활성 방법, 즉 깊이 맵이 주어진 범위 데이터 방법은 수치 근사 접근법에 의해 3D 프로파일을 재구성하고 모델을 기반으로 시나리오에서 객체를 구축한다.이러한 방법은 구조화된 빛, 레이저 거리 측정기 및 기타 활성 감지 기술 등 깊이 지도를 획득하기 위해 기계적으로 또는 방사계적으로 재구성된 물체를 능동적으로 간섭한다.기계적 방법의 간단한 예로는 깊이 게이지를 사용하여 턴테이블에 올려진 회전 물체까지의 거리를 측정할 수 있습니다.보다 적용 가능한 방사선 측정 방법은 물체를 향해 광도를 방출한 다음 반사된 부분을 측정합니다.예를 들어 움직이는 광원, 컬러 가시광선, 비행 시간 레이저부터 전자파 또는 3D 초음파까지 다양합니다.자세한 내용은 3D 스캔을 참조하십시오.

수동적 방법

수동적인 3D 재구성 방법은 재구성된 물체에 간섭하지 않으며, 물체 표면에 반사되거나 방출되는 광도를 측정하기 위해 센서를 사용하여 이미지 [8]이해를 통해 3D 구조를 추론합니다.일반적으로 센서는 가시광선에 민감한 카메라의 이미지 센서이며, 이 방법에 대한 입력은 디지털 이미지 세트(1개, 2개 이상) 또는 비디오입니다.이 경우 영상 기반 재구성에 대해 설명하며 출력은 3D 모델입니다.능동적 방법에 비해 수동적 방법은 보다 광범위한 [9]상황에 적용할 수 있다.

단안 단서법

단안 단서법은 한 시점(카메라)에서 1개 이상의 영상을 사용해 3D 시공으로 진행하는 것을 말한다.2D 특성(예: 실루엣, 쉐이딩 및 텍스처)을 활용하여 3D 형상을 측정하기 때문에 Shape-From-X라고도 합니다. 단안 큐를 통한 3D 재구성은 간단하고 빠르기 때문에 하나의 적절한 디지털 이미지만 있으면 충분합니다.엄밀히 말하면 스테레오 대응이 필요 없고,[10] 상당히 복잡합니다.

단일 또는 다중 뷰 깊이 지도 또는 실루엣에서 3D 모양 생성 및 재구성

쉐이딩으로부터의 형상 화상내의 쉐이딩 정보의 해석에 의해, 램버트 반사율을 이용해 물체 표면의 통상 정보의 깊이를 복원해 [12]재구축한다.

광도계 스테레오 이 접근법은 셰이딩 방식보다 더 정교합니다.다른 조명 조건에서 촬영된 영상을 사용하여 깊이 정보를 해결합니다.이 [13]방법에서는 여러 이미지가 필요합니다.

텍스처 형태 복제된 텍스처 단위로 덮인 매끄러운 표면을 가진 물체와 3D에서 2D로의 투영으로 인해 왜곡과 원근법이 발생한다고 가정합니다.2D 영상으로 측정한 왜곡과 원근감은 물체 [14]표면의 정상 정보의 깊이를 역방향으로 해결하기 위한 힌트를 제공한다.

스테레오 비전

주요 기사:컴퓨터 스테레오 비전

스테레오 비전은 인간 시각계의 [15]연구에 근거해 복수의 화상으로부터 물체의 3차원 기하학적 정보를 취득한다.결과는 깊이 지도의 형태로 나타납니다.서로 다른 시야각에서 동시에 두 대의 카메라에 의해 획득된 물체의 이미지 또는 서로 다른 시야각에서 서로 다른 시간에 하나의 카메라에 의해 획득된 물체의 이미지를 사용하여 3D 기하학적 정보를 복원하고 3D 프로필과 위치를 재구성하는 데 사용됩니다.이것은 쉐이딩에서 쉐이딩에서와 같은 단안법보다 더 직접적입니다.

쌍안경 스테레오 비전 방법은 광축이 평행한 두 대의 동일한 카메라가 동일한 물체를 관찰해야 하며, 서로 다른 관점에서 두 개의 이미지를 획득합니다.삼각관계에서는 시차로부터 깊이정보를 산출할 수 있다.양안 스테레오 비전 방식이 잘 개발되어 있으며, 3D 재구성에 안정적으로 기여하고 있어 다른 3D 구축에 비해 성능이 우수합니다.안타깝게도, 이 시스템은 계산 부하가 높을 뿐만 아니라 기준선 거리가 클 때는 성능이 다소 떨어집니다.

문제 기술 및 기본 사항

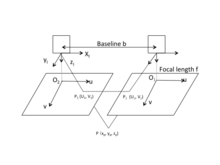
물체의 3D 기하학적 정보를 얻기 위해 쌍안경 스테레오 시각을 사용하는 접근 방식은 시각적 [16]불균형에 기초한다.다음 그림은 수평으로 보이는 양안 스테레오 비전의 간단한 도식도를 제공합니다. 여기서 b는 두 카메라의 투영 중심 사이의 기준선입니다.

입체계의 기하학

카메라 좌표계의 원점은 그림과 같이 카메라 렌즈의 광학 중심에 있습니다.사실, 카메라의 이미지 평면은 카메라 렌즈의 광학 중심 뒤에 있습니다.다만, 계산을 간단하게 하기 위해서, 렌즈의 광중심 앞에 f씩 화상을 그린다.영상 좌표계 v의u축 및 좌표계의 x축 및 y축과 각각 같은 방향에 있습니다.영상 좌표계의 원점은 영상 평면과 광축의 교차점에 있습니다.대응하는 이미지 포인트가 1, 1){}) 2, {}(}, 인 월드 P({P})를 왼쪽과 오른쪽 이미지 평면에 각각 표시한다고 가정합니다.두 대의 카메라가 동일한 평면에 있다고 하면P1({1})과P2({2})의 y값이 동일하다고 가정합니다. 즉, }= 삼각 관계에 따르면,

서( x , , p ){ ( x {p, y , z {} )는 왼쪽 카메라의 좌표계에 P { P}의 좌표이고 { f는 카메라의 초점 거리입니다.시각적 차이는 두 대의 카메라에 의해 획득된 특정 월드 포인트의 이미지 포인트 위치 차이로 정의됩니다.

P P의 좌표를 산출할 수 있습니다.

따라서 영상 포인트의 좌표를 알고 나면 두 카메라의 파라미터 외에 해당 포인트의 3D 좌표를 결정할 수 있습니다.

3D 재구성은 다음 섹션으로 구성됩니다.

이미지 취득

2D 디지털 영상 획득은 3D 재구성의 정보 소스입니다.일반적으로 사용되는 3D 재구성은 두 개 이상의 영상을 기반으로 하지만 경우에 따라 하나의 영상만 사용할 수도 있습니다.특정 애플리케이션의 시기 및 목적에 따라 다양한 유형의 이미지 획득 방법이 있습니다.어플리케이션의 요건뿐만 아니라 시각의 차이, 조도, 카메라의 성능, 시나리오의 특징도 고려해야 합니다.

카메라 보정

주요 기사:기하학적 카메라 보정

쌍안경 스테레오 비전에서의 카메라 보정은 이미지 1, 1{1 과 P2 2, 2u 2, v 2) {) 의 매핑 관계를 결정하는 것입니다. P},},})를 선택합니다카메라 보정은 쌍안경 스테레오 비전을 통한 3D 재구성의 기본적이고 필수적인 부분입니다.

기능 추출

주요 기사:기능 추출

특징 추출의 목적은 스테레오 대응이 처리되는 이미지의 특성을 얻는 것입니다.그 결과, 화상의 특성은 매칭 방법의 선택과 밀접하게 관련지어진다.이러한 특징 추출에 보편적으로 적용되는 이론은 없기 때문에 쌍안경 스테레오 비전 연구에서 스테레오 대응이 매우 다양해집니다.

스테레오 대응

주요 기사:이미지 등록

스테레오 대응은 이미지에서 1, 1 }(})과 2, 2 {와 하도록 이미지의 원시 요인 간의 대응 관계를 설정하는 것입니다.예를 들어 조명, 소음, 표면 물리적 특성 등과 같은 시나리오의 특정 간섭 인자를 주목해야 한다.

복원

정밀한 대응에 따라 카메라 위치 파라미터와 조합하여 3D 기하학적 정보를 어렵지 않게 복구할 수 있다.3D 재구성의 정확도는 대응 정밀도, 카메라 위치 파라미터 오류 등에 따라 달라지기 때문에 비교적 정확한 3D 재구성을 위해서는 이전 절차를 신중하게 수행해야 합니다.

3D 의료 영상 재구성

진단, 환자 추적, 컴퓨터 지원 수술, 수술 계획 등의 임상 루틴은 인체 해부학의 원하는 부분의 정확한 3D 모델을 통해 촉진됩니다.3D 재구성의 주된 동기는 다음과 같습니다.

  • 멀티뷰 집약을 통해 정확도가 향상되었습니다.
  • 상세한 표면 추정치.
  • 의사의 의료 시술 계획, 시뮬레이션, 안내 또는 기타 보조에 사용할 수 있습니다.
  • 환자 해부학의 정확한 위치와 방향을 결정할 수 있습니다.
  • 방사선 치료 계획 및 치료 검증, 척추 수술, 고관절 치환, 신경 중재 및 대동맥 스텐트 등 다양한 임상 분야에서 도움이 됩니다.

응용 프로그램:

3D 재구성은 다양한 분야에서 응용되고 있습니다.다음과 같은 것이 있습니다.

문제 설명:

대부분 3D 재구성에 사용할 수 있는 알고리즘은 매우 느리고 실시간으로 사용할 수 없습니다.제시된 알고리즘은 아직 초기 단계이지만 빠른 연산의 가능성이 있습니다.

기존 접근법:

Delaunay 삼각 측량(25점)

들뢰네 및 알파 형상

  • 딜라네이 방법은 초기 점 구름에서 사면체 표면을 추출하는 것을 포함한다.공간의 점 집합에 대한 '모양'의 개념은 알파 형상의 개념에 의해 주어진다.유한점 집합 S와 실제 파라미터 알파가 주어졌을 때, S의 알파 형상은 볼록하지도 않고 꼭 [29]연결된 것도 아닌 폴리토프(2차원 다각형과 3차원 다면체의 임의의 차원에 대한 일반화)이다.큰 값의 경우 알파 모양은 S의 볼록-헐과 동일합니다.에델스브루너와 무케가[30] 제안한 알고리즘은 α보다 작은 주변 구에 의해 구분되는 모든 사면체를 제거한다.그 후 표면은 결과 [30]사면체에서 외부 삼각형으로 구해진다.
  • Tight[31] Cocone이라고 불리는 또 다른 알고리즘은 초기 4면체를 내부와 외부로 라벨링합니다.내부 및 외부에 있는 삼각형이 결과 표면을 생성합니다.

두 가지 방법 모두 노이즈가 [31]있는 점 구름을 재구성하기 위해 최근에 확장되었습니다.이 방법에서는 점의 품질에 따라 방법의 실현 가능성이 결정됩니다.전체 점 구름 세트를 사용하기 때문에 정확한 삼각측량을 위해 임계값보다 높은 오차를 가진 지표면의 점이 재구성된 [29]지오메트리에 명시적으로 표시됩니다.

행군 큐브

제로 세트 방식

표면 재구성은 공간 내의 각 점에 표면 S에 대해 서명된 거리를 할당하는 거리 함수를 이용해 이루어진다.오브젝트의 다각형 표현을 얻기 위해 사용되는 제로 세트를 추출하기 위해 등고선 알고리즘이 사용된다.따라서 비조직화된 점 구름에서 표면을 재구성하는 문제는 샘플링된 점의 경우 0의 값을 갖는 적절한 함수 f의 정의로 축소되고 나머지 점의 경우 0의 값으로 바뀐다.행진 큐브라고 불리는 알고리즘은 이러한 방법의 [32]사용을 확립했다.주어진 알고리즘에는 다양한 변형이 있으며, 일부는 이산 함수 f를 사용하는 반면, 다른 일부는 초기 포인트 [33][34]세트를 조정하는 데 다화파 방사 기저 함수를 사용합니다.포아송 방정식을 기반으로 한 최소 제곱 이동, 로컬 [35]지원이 있는 기본 함수 등도 사용되었습니다.극한 곡률 영역(예: 모서리, 모서리)에서 지오메트리 정밀도가 손실되는 것이 주요 문제 중 하나입니다.또, 정보의 전처리는, 모종의 필터링 기술을 적용함으로써, 코너의 정의에 영향을 주는 것으로, 코너를 부드럽게 한다.모서리 검출 및 미세화를 위해 재구성에 사용되는 후처리 기법과 관련된 여러 연구가 있지만,[36] 이러한 방법은 솔루션의 복잡성을 증가시킨다.

볼륨 렌더링 기능을 갖춘 솔리드 지오메트리 이미지 제공: UC 산타바바라, Patrick Chris Fragile 박사

VR 기술

개체의 전체 볼륨 투명도는 VR 기술을 사용하여 시각화됩니다.영상은 볼륨 데이터를 통해 광선을 투사하여 수행됩니다.각 광선을 따라 모든 복셀에서 불투명도와 색상을 계산해야 합니다.그러면 각 광선을 따라 계산된 정보가 영상 평면의 픽셀로 집계됩니다.이 기술은 사물의 전체 콤팩트한 구조를 종합적으로 볼 수 있도록 도와줍니다.이 기술에는 엄청난 양의 계산이 필요하기 때문에 저콘트라스트 데이터에는 강력한 구성 컴퓨터가 적합합니다.다음과 같이 광선을 투영하는 두 가지 주요 방법을 고려할 수 있습니다.

  • 오브젝트 오더 방법: 투사 광선은, 볼륨으로부터 전면(볼륨으로부터 화상 평면까지)을 통과합니다.
  • 이미지 순서 또는 레이캐스팅 방법: 투사 광선은 전면에서 후면(이미지 평면에서 볼륨으로)을 통과합니다.합성 이미지에는 몇 가지 다른 방법이 있으며 사용자의 목적에 따라 적절한 방법이 있습니다.의료 영상에서 일반적인 방법으로는 MIP(최대 강도 투영), MinIP(최소 강도 투영), AC(알파 합성) 및 NPVR(비사실 볼륨 렌더링)이 있습니다.
복셀 그리드를 통해 광선을 추적합니다.표준 8 연결 알고리즘을 사용하여 선택된 복셀 외에 횡단되는 복셀이 해치로 표시됩니다.

복셀 그리드

이 필터링 기술에서는 입력 공간을 3D 복셀 그리드를 사용하여 샘플링하여 포인트 [37]수를 줄입니다.각 복셀에 대해 모든 점을 대표하는 것으로 중심점이 선택됩니다.복셀 중심 선택 또는 복셀 내에 있는 점의 중심을 선택하는 두 가지 방법이 있습니다.내부 포인트를 얻는 평균은 계산 비용이 더 높지만 더 나은 결과를 제공합니다.따라서, 입력 공간의 서브셋이 대략적으로 밑면을 나타내는 것을 얻을 수 있다.Voxel 그리드 방법은 표면을 나타내는 최종 포인트 수를 정의할 수 없음, 복셀 내부의 포인트 감소로 인한 기하학적 정보 손실, 노이즈가 많은 입력 공간에 대한 민감도 등 다른 필터링 기술과 동일한 문제를 일으킵니다.

「 」를 참조해 주세요.

레퍼런스

  1. ^ Moons, Theo, Luc Van Gool, Maarten Vergauwen."여러 이미지에서 3D 재구성 파트 1: 원리"컴퓨터 그래픽스 및 비전 4.4(2010): 287-404.
  2. ^ 졸호퍼, 미카엘 등"RGB-D카메라를 사용한 실시간 비강성 재구성"그래픽스 33.4에서의 ACM 트랜잭션(2014): 156.
  3. ^ "The Future of 3D Modeling". GarageFarm. 2017-05-27. Retrieved 2017-05-27.
  4. ^ a b Liping Zheng; Guangyao Li; Jing Sha (2007). "The survey of medical image 3D reconstruction". Fifth International Conference on Photonics and Imaging in Biology and Medicine. Proceedings of SPIE. Vol. 6534. pp. 65342K–65342K–6. doi:10.1117/12.741321. S2CID 62548928.
  5. ^ 보셀만, 조지, 샌더 다이크만."포인트 클라우드 및 지상도에서 3D 빌딩 모델을 재구성합니다."사진 측량 원격 감지 및 공간 정보 과학 국제 아카이브 34.3/W4(2001): 37-44.
  6. ^ 콜레산티, 카를로, 야누시 와소스키."우주 전달식 합성 개구 레이더(SAR) 간섭계로 산사태 조사"엔지니어링 지질학 88.3-4(2006) : 173-199.
  7. ^ a b Mahmoudzadeh, Ahmadreza; Golroo, Amir; Jahanshahi, Mohammad R.; Firoozi Yeganeh, Sayna (January 2019). "Estimating Pavement Roughness by Fusing Color and Depth Data Obtained from an Inexpensive RGB-D Sensor". Sensors. 19 (7): 1655. Bibcode:2019Senso..19.1655M. doi:10.3390/s19071655. PMC 6479490. PMID 30959936.
  8. ^ 부엘토프, 하인리히 H., 앨런 L.Yuille."Shape-from-X: Wayback Machine에서 2011-01-07년 정신물리학 및 계산 아카이브"섬유회사 91번지, 매사추세츠 주 보스턴 국제광학회, 1991년
  9. ^ Moons, Theo (2010). 3D reconstruction from multiple images. Part 1, Principles. Gool, Luc van., Vergauwen, Maarten. Hanover, MA: Now Publishers, Inc. ISBN 978-1-60198-285-8. OCLC 607557354.
  10. ^ Saxena, Ashutosh; Sun, Min; Ng, Andrew Y. (2007). "3-D Reconstruction from Sparse Views using Monocular Vision". 2007 IEEE 11th International Conference on Computer Vision: 1–8. CiteSeerX 10.1.1.78.5303. doi:10.1109/ICCV.2007.4409219. ISBN 978-1-4244-1630-1. S2CID 17571812.
  11. ^ Soltani, A.A.; Huang, H.; Wu, J.; Kulkarni, T.D.; Tenenbaum, J.B. (2017). "Synthesizing 3D Shapes via Modeling Multi-View Depth Maps and Silhouettes With Deep Generative Networks". Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. pp. 1511–1519 – via GitHub.
  12. ^ 혼, 버톨드 KP.「쉐이딩으로부터 형상화: 하나의 뷰로부터 매끄러운 불투명 물체의 형상을 얻는 방법」(1970).
  13. ^ Woodham, Robert J. (1980). "Photometric method for determining surface orientation from multiple images" (PDF). Optical Engineering. 19 (1): 138–141. Bibcode:1980OptEn..19..139W. doi:10.1117/12.7972479. Archived from the original (PDF) on 2014-03-27.
  14. ^ Witkin, Andrew P. (1981). "Recovering surface shape and orientation from texture" (PDF). Artificial Intelligence. 17 (1–3): 17–45. doi:10.1016/0004-3702(81)90019-9.
  15. ^ Kass, Michael; Witkin, Andrew; Terzopoulos, Demetri (1988). "Snakes: Active contour models" (PDF). International Journal of Computer Vision. 1 (4): 321–331. doi:10.1007/BF00133570. S2CID 12849354.
  16. ^ 맥카운, 자크, 그리고 루시엔 리브스.양안시: 발달, 깊이 지각 및 장애.노바 사이언스 퍼블리셔스, 2010년
  17. ^ Mahmoudzadeh, Ahmadreza; Yeganeh, Sayna Firoozi; Golroo, Amir (2019-07-09). "3D pavement surface reconstruction using an RGB-D sensor". arXiv:1907.04124 [cs.CV].
  18. ^ 캐런자, 조엘 등"인간 배우들의 프리포인트 영상"그래픽스상의 ACM 트랜잭션.제22권No.3. ACM, 2003.
  19. ^ 스룬, 세바스찬"로봇 지도 제작: 설문 조사"새천년의 인공지능 탐구 1.1-35(2002년) : 1.
  20. ^ Poullis, Charalambos; You, Suya (May 2011). "3D Reconstruction of Urban Areas". 2011 International Conference on 3D Imaging, Modeling, Processing, Visualization and Transmission: 33–40. doi:10.1109/3dimpvt.2011.14. ISBN 978-1-61284-429-9. S2CID 1189988.
  21. ^ 쉬, 팡, 클라우스 뮐러."Wayback Machine에서 2016-03-19년 아카이브된 범용 그래픽 하드웨어를 사용하여 실시간 3D 컴퓨터 단층 촬영 재구성"의학 및 생물학 분야 물리학 52.12 (2007) : 3405.
  22. ^ a b 모타라, 미켈라 등"진지한 게임으로 문화유산 배우기." 문화재저널 15.3(2014) : 318-325.
  23. ^ 브루노, 파비오 등"3D 재구축에서 가상 현실까지: 디지털 고고학 전시를[dead link] 위한 완벽한 방법론." 문화재 저널 11.1 (2010) : 42-49.
  24. ^ 이자디, 샤람 등"KinectFusion: 움직이는 깊이 카메라를 사용하여 실시간 3D 재구성과 상호작용"사용자 인터페이스 소프트웨어와 테크놀로지에 관한 제24회 연례 ACM 심포지엄의 속행.ACM, 2011.
  25. ^ Wang, Jun; Gu, Dongxiao; Yu, Zeyun; Tan, Changbai; Zhou, Laishui (December 2012). "A framework for 3D model reconstruction in reverse engineering". Computers & Industrial Engineering. 63 (4): 1189–1200. doi:10.1016/j.cie.2012.07.009.
  26. ^ Moeslund, Thomas B., 그리고 Erik Granum."컴퓨터 비전에 기반한 인간의 모션 캡처에 대한 조사입니다."컴퓨터 비전과 이미지 이해 81.3(2001) : 231-268.
  27. ^ 헤자라티, 모센, 데바 라마난."합성에 의한 분석: 객체 재구성에 의한 3D 객체 인식"컴퓨터 비전과 패턴 인식에 관한 IEEE 회의의 진행.2014.
  28. ^ 케스킨, 켐, 애세 에르칸, 랄레 아카룬."hmm을 사용하여 인터랙티브 인터페이스를 위한 실시간 핸드 트래킹과 3D 제스처 인식"ICANN/ICONIPP 2003 (2003) : 26-29.
  29. ^ a b Angelopoulou, A.; Psarrou, A.; Garcia-Rodriguez, J.; Orts-Escolano, S.; Azorin-Lopez, J.; Revett, K. (20 February 2015). "3D reconstruction of medical images from slices automatically landmarked with growing neural models" (PDF). Neurocomputing. 150 (Part A): 16–25. doi:10.1016/j.neucom.2014.03.078. hdl:10045/42544.
  30. ^ a b Edelsbrunner, Herbert; Mücke, Ernst (January 1994). "Three-dimensional alpha shapes". ACM Trans. Graph. 13 (1): 43–72. arXiv:math/9410208. Bibcode:1994math.....10208E. doi:10.1145/174462.156635.
  31. ^ a b Dey, Tamal K.; Goswami, Samrat (August 2006). "Probable surface reconstruction from noisy samples". Computational Geometry. 35 (1–2): 124–141. doi:10.1016/j.comgeo.2005.10.006.
  32. ^ Lorensen, William E.; Cline, Harvey E. (July 1987). "Marching cubes: A high resolution 3d surface construction algorithm". SIGGRAPH Comput. Graph. 21 (4): 163–169. CiteSeerX 10.1.1.545.613. doi:10.1145/37402.37422.
  33. ^ Hoppe, Hugues; DeRose, Tony; Duchamp, Tom; McDonald, John; Stuetzle, Werner (July 1992). "Surface reconstruction from unorganized points". SIGGRAPH Comput. Graph. 26 (2): 71–78. CiteSeerX 10.1.1.5.3672. doi:10.1145/142920.134011.
  34. ^ Carr, J.C.; Beatson, R.K.; Cherrie, J.B.; Mitchell, T.J.; Fright, W.R.; McCallum, B.C.; Evans, T.R. (2001). "Reconstruction and representation of 3d objects with radial basis functions" (PDF). 28th Annual Conference on Computer Graphics and Interactive Techniques SIGGRAPH 2001. ACM. pp. 67–76.
  35. ^ Walder, C.; Schölkopf, B.; Chapelle, O. (2006). "Implicit Surface Modelling with a Globally Regularised Basis of Compact Support" (PDF). Eurographics. 25 (3). Archived from the original (PDF) on 2017-09-22. Retrieved 2018-10-09.
  36. ^ Wang, C.L. (June 2006). "Incremental reconstruction of sharp edges on mesh surfaces". Computer-Aided Design. 38 (6): 689–702. doi:10.1016/j.cad.2006.02.009.
  37. ^ Connolly, C. (1984). "Cumulative generation of octree models from range data". Proceedings of the 1984 IEEE Conference on Robotics and Automation. 1: 25–32. doi:10.1109/ROBOT.1984.1087212.

외부 링크

무료 사전인 Wiktionary에서 3D 재구성을 찾아보십시오.

외부 링크