Hough 변환

피쳐 검출
에지 검출
캐니 데리히 미분 소벨 프리윗 로버츠 크로스
코너 감지
해리스 연산자 시·토마시 레벨 곡선 곡면성 헤시안 형상 강도 측정 수잔. FAST
블롭 검출
가우스 공화국의 라플라시안 (LoG) 가우스인의 차이(DoG) 헤시안 결정계수(DoH) 최대 안정적 극한 지역 PCBR
능선 검출
Hough 변환
Hough 변환 일반화 Hough 변환
구조 텐서
구조 텐서 일반화 구조 텐서
부착 불변 피쳐 검출
아핀 형태 적응 해리스 아핀 헤시안 어바인
피쳐 설명
시프트 서핑 글로 HOG
축척 공간
축척 공간 공리 이행내역 피라미드
v t

Hough 변환은 이미지 분석, 컴퓨터 비전, 디지털 이미지 처리에 사용되는 형상 추출 기법이다.^[1]이 기법의 목적은 투표 절차에 의해 특정 종류의 형상 내에서 물체의 불완전한 예를 찾는 것이다.이 투표 절차는 Hough 변환 계산 알고리즘에 의해 명시적으로 구성된 소위 축전지 공간에서 개체 후보가 로컬 최대값으로 획득되는 매개변수 공간에서 수행된다.

고전적인 Hough 변환은 이미지에서 선들의 식별과 관련이 있었지만, 후에 Houg 변환은 가장 흔히 원이나 타원처럼 임의 모양의 위치를 식별하는 것으로 확장되었다.오늘날 보편적으로 사용되고 있는 Hough 변환은 Richard Duda와 Peter Hart에 의해 1972년에 발명되었는데, 그는 Paul Hough와 관련된 1962년 특허 이후에 이것을 "일반화된 Houg 변환"^[2]이라고 불렀다.^[3][4]이 변환은 다나 H. 발라드에 의해 컴퓨터 비전 커뮤니티에서 1981년 저널 "임의의 형태를 감지하기 위한 Hough 변환 일반화"를 통해 대중화되었다.

역사

그것은 처음에 버블 챔버 사진의 기계 분석을 위해 발명되었다(Hough, 1959).

Hough 변환은 1962년 미국 특허 306만9,654로 특허를 받았으며, "복잡한 패턴을 인식하는 방법과 수단"이라는 이름으로 미국 원자력 위원회에 할당되었다.이 특허는 직선에는 경사 절편 파라메트리제이션(Slope Intercept parametrization)을 사용하며, 이는 경사가 무한대로 갈 수 있기 때문에 어색하게 무한 변형 공간으로 이어진다.

오늘날 보편적으로 사용되는 rho-theta parametrization은 에서 처음 설명되었다.

Duda, R.O.; Hart, P. E. (January 1972). "Use of the Hough Transformation to Detect Lines and Curves in Pictures". Comm. ACM. 15: 11–15. doi:10.1145/361237.361242.

적어도 1930년대 이후 라돈 변형의 표준이 되었지만.

오고만과 클로웨스의 변화는 에 설명되어 있다.

O'Gorman, Frank; Clowes, MB (1976). "Finding Picture Edges Through Collinearity of Feature Points". IEEE Trans. Comput. 25 (4): 449–456. doi:10.1109/TC.1976.1674627.

현대적인 형태의 Hough 변혁이 어떻게 발명되었는지에 대한 이야기는 에서 전해진다.

Hart, P. E. (November 2009). "How the Hough Transform was Invented" (PDF). IEEE Signal Processing Magazine. 26 (6): 18–22. doi:10.1109/msp.2009.934181. S2CID 16245096. Archived from the original (PDF) on 2018-05-16.

이론

디지털 영상의 자동 분석에서 종종 직선, 원 또는 타원 같은 단순한 모양을 감지하는 데 문제가 발생한다.대부분의 경우 에지 검출기를 영상 공간에서 원하는 곡선에 있는 영상 포인트 또는 영상 픽셀을 얻기 위한 사전 처리 단계로 사용할 수 있다.그러나 이미지 데이터 또는 가장자리 검출기의 결함으로 인해 원하는 곡선에는 누락된 점이나 픽셀뿐 아니라 가장자리 검출기에서 얻을 수 있는 이상적인 선/원/엘리프(원/엘리프)와 노이즈가 있는 가장자리 점 사이의 공간 편차가 있을 수 있다.이러한 이유로, 추출된 가장자리 형상을 적절한 선, 원 또는 타원 집합으로 그룹화하는 것은 종종 비경쟁적이다.Hough 변환의 목적은 매개변수화된 이미지 객체 집합(Shapiro 및 Stockman, 304)에 대해 명시적 투표 절차를 수행함으로써 에지 포인트를 객체 후보로 그룹화하는 것을 가능하게 함으로써 이 문제를 해결하는 것이다.

선 탐지

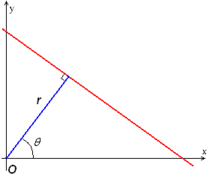
Hough 변환의 가장 간단한 경우는 직선을 검출하는 것이다.일반적으로 직선 y = mx + b는 매개변수 공간에서 점(b, m)으로 나타낼 수 있다.그러나 수직선은 문제를 제기한다.그들은 경사 매개변수 m의 무한 값을 발생시킬 것이다.따라서, 계산상의 이유로, Duda와^[5] Hart는 헤세 정상 형태의 사용을 제안했다.

$\displaystyle r=x\cos \theta +y\sin \theta ,}$

여기서 $r{\displaystyle }$ ${\displaystyle r}$은(는) 원점에서 직선상의 가장 가까운 지점까지의 거리이고$$, $\theta {\displaystyle }$ ${\displaystyle \theta}$은 $x{\displaystyle }$ ${\displaystyle x}$축과$$ 원점을 그 가장 가까운 지점과 연결하는 선 사이의 각도다$$.

이 형태의 직관은 평면 방정식과 유사하게 선의 모든 벡터가 원점에서 오는 길이$$ $r{\displaystyle }$ ${\displaystyle r}$의 직선과 직각(직교)이어야 한다는 것이다.It is easy to see that the intersection point of the function line and the perpendicular line that comes from the origin is at ${\displaystyle P_{0}=(r\cos \theta ,r\sin \theta )}$. So, for any point ${\displaystyle P}$ on the line, the vector ${\displaystyle P-P_{0}}$ must be ort벡터 ${\displaystyle {P\mathrm{}}_{}}$ ${\displaystyle 0{}_{}}$- 0${\displaystyle }$= ${\displaystyle {P\mathrm{}}_{}}$ 0 ${\$에 대한 호칭$P_{0$따라서 함수 라인의 $모든$ 점 P${\displaystyle }$=${\displaystyle }$( ${\displaystyle x}$, ${\displaystyle y}$) ${\displaystyle$ P$=(x,y)}$에 대해 방정식$({\displaystyle P}$- ${\displaystyle {P\mathrm{}}_{}}$ ${\displaystyle {}_{}}$) ${\displaystyle \cdot }$ ${\displaystyle {}_{}}$ ${\displaystyle 0{}_{}}$= 0 ${\displaystyle (P-P_{0})\cdot P_{0}=0}$이 충족되어야 한다는$$ 것을 알게 된다.Therefore, ${\displaystyle P\cdot P_{0}=P_{0}\cdot P_{0}}$. Since ${\displaystyle P=(x,y)}$ and ${\displaystyle P_{0}=(r\cos \theta ,r\sin \theta )}$, we get ${\displaystyl$$e r(x\cos \theta +y\sin \theta )=r^{2}(\cos ^{2}\theta +\sin ^{2}\theta )}$. Since ${\displaystyle \cos ^{2}\theta +\sin ^{2}\theta =1}$, we get the final form of ${\displaystyle x\cos \theta +y\sin \theta =r}$.

따라서 이미지의 각 선과 한 쌍$({\displaystyle r,}$ ${\displaystyle \theta }$) ${\displaystyle(r,\theta )}$을(를) 연결할 수 있다$.$$({\displaystyle }$ ${\displaystyle r}$ ,${\displaystyle \theta }$) ${\displaystyle (r,\theta )}$ 평면은$$ 때때로 2차원의 직선 집합에 대한 Hough space라고 한다.이러한 표현은 허우를 개념적으로 2차원 라돈 변형에 매우 가깝게 만든다.사실, Houg 변환은 수학적으로 라돈 변환과 동일하지만, 두 변환은 전통적으로 그것과 관련된 다른 계산적 해석을 가지고 있다.^[6]

평면에 하나의 점이 주어진다면, 그 점을 통과하는 모든 직선의 집합은 (r, θ) 평면의 사인곡선에 해당하며, 그 점에 고유한 것이다.직선을 형성하는 두 개 이상의 점 세트는 그 선에 대한 (r, ))에서 사인파가 교차한다.따라서 공선점 검출 문제는 동시곡선을 찾는 문제로 전환될 수 있다.^[7]

실행

선형 Hough 변환 알고리즘은 직선을 정의하는 두 파라미터를 추정한다.변환 공간은 2차원이 있으며, ${\displaystyle \mathrm{변환}}$ 공간의 모든 지점은 축전지로 $사용$되어 r${\displaystyle }$= x ${\displaystyle \cos \theta }$ + ${\displaystyle y}$ ${\displaystyle \sin }$ ${\displaystyle \theta }$ θ${\displaystyle }$θ ${\displaystyle \{}$ { { {$$\$displaystyle r=x$\cos$\theta \cos$\the$}.$ 이미지의 검출된 가장자리의 모든 지점은 축전기에 기여한다$.$

축열조의 치수는 알 수 없는 매개변수의 수, 즉, 두 개의 매개변수에서 r과 θ의 정량화된 값을 고려한다(r, θ).(x, y) 및 그 부근의 각 픽셀에 대해 Hough 변환 알고리즘은 해당 픽셀에 직선의 증거가 충분한지 여부를 결정한다.그렇다면 해당 라인의 파라미터(r, θ)를 계산한 다음 파라미터가 들어가는 축전지의 bin을 찾아 해당 bin의 값을 증가시킨다.

가장 높은 값을 가진 빈을 찾음으로써, 일반적으로 축전지 공간에서 국부적인 맥시마를 찾음으로써, 가장 가능성이 높은 선을 추출할 수 있으며, 그 (대략적인) 기하학적 정의를 읽어낼 수 있다(샤피로와 스톡맨, 304).이러한 최고점을 찾는 가장 간단한 방법은 어떤 형태의 임계값을 적용하는 것이지만, 다른 기법들은 다른 상황에서 더 나은 결과를 산출할 수 있다. 즉, 어떤 선이 몇 개인지와 몇 개인지 결정하는 것이다.반환되는 선에는 길이 정보가 없으므로 다음 단계에서 이미지의 어느 부분이 어느 선과 일치하는지 찾아야 하는 경우가 많다.더욱이, 가장자리 감지 단계의 불완전한 오류로 인해, 축열조 공간에 대개 오류가 있을 것이며, 이는 적절한 피크를 찾는 것을 비독점적으로 만들 수 있으며, 따라서 적절한 라인을 찾을 수 없다.

선형 Hough 변환의 최종 결과는 축전지와 유사한 2차원 배열(매트릭스)이다. 이 매트릭스의 한 차원은 정량화된 각도 θ이고, 다른 차원은 정량화된 거리 r이다.행렬의 각 요소는 정량화된 매개변수(r, ,)로 표현되는 선에 위치하는 점 또는 픽셀의 합과 같은 값을 갖는다.따라서 값이 가장 높은 요소는 입력 영상에 가장 많이 나타나는 직선을 나타낸다.^[8]

예

예 1

여기에 검은색 점으로 표시된 세 개의 데이터 점을 고려하십시오.

• 각 데이터 점에 대해, 그것을 통과하는 여러 선들이 모두 다른 각도로 표시된다.이것들은 여기에 다른 색깔로 보여진다.
• Hough 변환은 탐지된 가장자리에 있는 모든 픽셀의 기여를 누적한다.각 선에 수직이며 원점을 교차하는 지지선이 존재한다.각각의 경우에, 이것들 중 하나는 화살표로 보여진다.
• 각 지지선의 길이(즉, 원점에 대한 수직 거리)와 각도가 계산된다.길이와 각도는 도표 아래에 표로 표시되어 있다.

계산 결과 어느 경우든 60°의 지지선의 길이가 비슷함을 알 수 있다.따라서 해당 선(위 그림의 파란색 선)은 매우 유사한 것으로 파악된다.따라서 모든 포인트가 파란 선에 가깝게 놓여 있다고 가정할 수 있다.

예 2

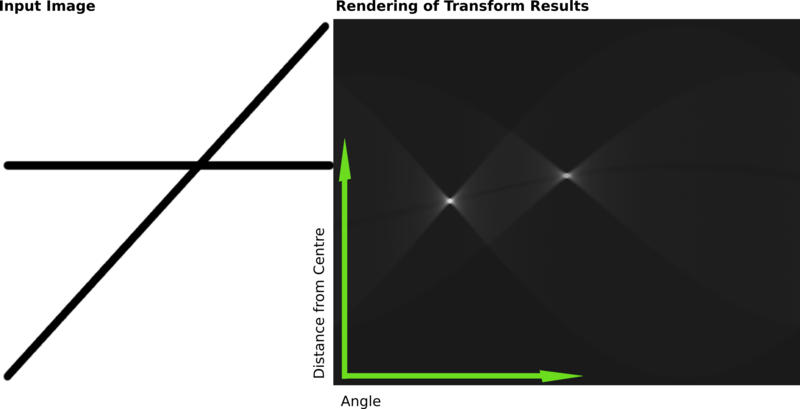
다음은 두 굵은 선이 포함된 래스터 영상에서 허우 변환의 결과를 보여주는 다른 예다.

이 변환의 결과는 매트릭스에 저장되었다.셀 값은 모든 점을 통과하는 곡선의 수를 나타낸다.높은 셀 값은 더 밝게 렌더링된다.뚜렷하게 밝은 두 점은 두 선의 Hough 매개변수다.이러한 점의 위치에서 입력 영상에 있는 두 선의 영상 중심으로부터의 각도 및 거리를 결정할 수 있다.

변형 및 확장

그라데이션 방향을 사용하여 투표 수 감소

영상 강도의 국부적인 그라데이션이 반드시 가장자리와 직교해야 한다는 점을 고려한다면 오고만과 클로웨스가 제안한 개선을 사용하여 선을 검출할 수 있다.가장자리 감지에는 일반적으로 강도 구배 크기 계산이 포함되기 때문에, 구배 방향은 종종 부작용으로 발견된다.주어진 좌표점(x,y)이 실제로 선상에 있는 경우, 그라데이션의 국부 방향은 해당 선에 해당하는 θ 파라미터를 부여하고, r 파라미터를 즉시 구한다.(샤피로와 스톡맨, 305) 구배 방향은 20° 이내로 추정할 수 있으며, 이는 정현상 궤적을 180°에서 약 45°로 단축시킨다.이렇게 하면 계산 시간이 단축되고 쓸모없는 표의 수를 줄이는 흥미로운 효과가 있어 이미지 속 실제 라인에 해당하는 스파이크의 가시성이 향상된다.

커널 기반 Hough 변환(KHT)

페르난데스, 올리베이라 등은 비교적 큰 이미지(예: 1280×960)에서도 소프트웨어 구현이 실시간 성능을 달성할 수 있도록 하는 Hough 변환의 개선된 투표 방식을 제안했다.커널 기반 Hough 변환은 Duda와 Hart가 제안한 것과 동일한${\displaystyle }$(${\displaystyle r}$ ,${\displaystyle )}$ $){\displaystyle (r,\theta )}$ 매개변수를 사용하지만 대략 콜린어 픽셀의 클러스터에서 작동한다.각 군집에 대해, 해당 군집에 대한 최적 맞춤 선과 관련된 불확실성을 모델링하는 지향적인 타원형-가우스 커널을 사용하여 표를 던진다.이 접근방식은 투표 제도의 성능을 크게 향상시킬 뿐만 아니라 훨씬 더 깨끗한 축전지를 생산하고 가짜 회선 검출에 대한 변환을 더욱 견고하게 한다.

평면 탐지를 위한 3-D 커널 기반 Hough 변환(3DK)HT)

림베르거와 올리베이라는^[10] 비조직적인 점 구름에서 비행기 탐지를 위한 결정론적 기법을 제안했는데, 비용은 샘플 수에서$$ ${\displaystyle \log }$ ${\displaystyle }$ ($){\displaystyle$ n$\log(n)}$이며, 비교적 큰 데이터셋의 실시간 성능을 달성했다(3.4GHz ${\displaystyle {\mathrm{CPU}}^{}}$에서 최대 ${\displaystyle {10\mathrm{}}^{}}$ 5 ${\$이것은 KHT(Kernel-based Hough transform)에서 영감을 받아 평면 지역을 위한 빠른 Hough-transform 투표 전략에 기초하고 있다.이 3D 커널 기반 Hough 변환(3DKHT)은 빠르고 강력한 알고리즘을 사용하여 대략적인 공동 평면 샘플의 클러스터를 분할하고, 3변량 가우스 커널을 사용하는 구면 축전지의 a($$${\displaystyle }$,${\displaystyle }$(, ${\displaystyle \varphi ,}$ ϕ, ρ, ${\displaystyle \rho }$, ρ, ${,$\,\$rho$})에서 (개별 샘플 대신) 개별 클러스터에 대해 표를 던졌다.이 접근방식은 RHT, RANSAC와 같은 점 구름에서의 평면 탐지에 대한 기존(비결정론적) 기법보다 몇 배나 빠른 크기 순이며 데이터 집합의 크기에 따라 더 잘 확장된다.대규모 데이터셋에서 평면 기능을 신속하게 탐지해야 하는 모든 애플리케이션과 함께 사용할 수 있다.

곡선의 강한 변형과 분석적 및 비분석적 도형에 대한 일반화

위에서 설명한 변환의 버전은 직선을 찾는 데만 적용되지만, 매개변수 집합으로 나타낼 수 있는 형상을 찾기 위해 유사한 변환을 사용할 수 있다.예를 들어 원은 중심과 반경을 나타내는 세 개의 매개변수 집합으로 변형될 수 있으므로, 후우 공간은 3차원이 된다.임의의 타원과 곡선은 매개변수 집합으로 쉽게 표현될 수 있는 형태와 마찬가지로 이러한 방식으로도 찾을 수 있다.

입체성이 있는 공간에서 분석적 형태를 검출하기 위한 Houg 변환의 일반화는 Fernandes와 Oliveira에 의해 제안되었다.^[11]분석 도형에 대한 다른 Hough 변환 기반 접근법과 대조적으로, Fernandes의 기술은 탐지하고자 하는 도형이나 입력 데이터 유형에 의존하지 않는다.제안된 공식은 변경되지 않은 채 데이터가 인코딩된 기하학(예: 유클리드 공간, 투영 공간, 등정형 기하학 등)의 가정된 모델을 변경하여 탐지를 분석형식의 한 유형으로 유도할 수 있다.또한, 의도된 형상들이 가능한 가장 적은 수의 매개변수로 표현되도록 보장하며, 다른 치수 및 다른 기하학적 정의를 가진 입력 집합에 가장 잘 맞는 다양한 종류의 형상들을 동시에 검출할 수 있게 한다(예를 들어, 가장 우수한 평면과 구의 동시 검출).점, 직선과 원의 집합이다.

평면 내 더 복잡한 형상(즉, 일부 2D 공간에서 분석적으로 표현할 수 없는 형상)의 경우, 미리 정의된 조회 표를 사용하여 형상의^[12] 특정 위치, 방향 및/또는 스케일링에 대해 형상이 투표할 수 있도록 하는 Generalized Hough 변환을 사용한다.Hough 변환은 탐지된 가장자리에 있는 모든 픽셀의 기여를 누적한다.

원 감지 프로세스

선 대신 원형을 검출하기 위해 알고리즘을 변경하는 것은 비교적 간단하다.

• 먼저 각 픽셀마다 셀로 구성된 축전지 공간을 만든다.처음에 각 셀은 0으로 설정된다.
• 영상의 각 에지점(${\displaystyle i}$, j)에 대해 원$({\displaystyle }$i -${\displaystyle }$a${\displaystyle {}^{}}$ 2${\displaystyle {}^{}}$+${\displaystyle }$( ${\displaystyle j}$- ${\displaystyle b{}^{}}$) 2${\displaystyle {}^{}}$= r ${\displaystyle {2\mathrm{}}^{}}$ ${\$ 원의 중심이 될 수 있는$$ 모든 셀을 증분한다.이 셀들은 방정식의 $문자$ a ${\displaystyle a}$로 표현된다.
• 이전 단계에서 발견된$$ ${\displaystyle a}$의 가능한 각 값에 대해 방정식을 충족하는$$ $b{\displaystyle }$ ${\displaystyle b}$의 가능한 모든 값을 찾으십시오.
• 축전지 공간에서 로컬 최대값을 검색하십시오.이 셀들은 알고리즘에 의해 탐지된 원을 나타낸다.

만약 우리가 미리 찾으려는 원의 반지름을 알지 못한다면, 우리는 3차원 축전지 공간을 사용하여 임의의 반지름을 가진 원을 검색할 수 있다.당연히 이것은 계산적으로 더 비싸다.

이 방법은 또한 원의 면적이 그 안에 여전히 충분히 존재하는 한 축전지 공간 밖에 부분적으로 있는 원도 감지할 수 있다.

3D 물체(플레인 및 실린더) 검출

또한 Hough 변환은 범위 데이터 또는 3D 포인트 클라우드에서 3D 객체를 검출하는 데 사용될 수 있다.비행기 탐지를 위한 고전적인 Hough 변환의 확장은 꽤 간단하다.평면은 x$$${\displaystyle {}_{}}$ x${\displaystyle }$+ ${\displaystyle {}_{}}$+ ${\displaystyle d}$(\$displaystyle$ z$=a_{x}x+a_$${$$y}$$y+$d$}$에 $해당$하는 $3D{\displaystyle {}_{}}$ Hough 공간을 ${\displaystyle {사용}_{}}$할 수 있는 명시적 $방정식{\displaystyle }$ $z$${\displaystyle }$= ${\displaystyle {}_{}}$ + y +$$$d$로 표현된다$.$이 확장은 2D 상대와 동일한 문제를 겪는다. 즉, 거의 수평면을 신뢰성 있게 검출할 수 있는 반면 평면 방향이 수직이 되면 성능이 악화된다(${\$ 및$$ ${\displaystyle y_{}}$ ${\$$}).$이 평면 구성은 공중 레이저 스캔에서 획득한 점 구름에서 평면을 검출하는 데 사용되었고 그 영역에서 모든 평면이 거의 수평이기 때문에 매우 잘 작동한다.

Houg 변환을 사용한 일반화 평면 검출의 경우 평면은 정상 $벡터{\displaystyle }$ n ${\displaystyle n}($구면 좌표 사용) 및 원점으로부터의 거리 $\rho {\displaystyle }$ ${\displaystyle \rho }$에 의해 파라메트리되어 3차원 Hough 공간이 발생할 수 있다.이것은 Hough 공간의 정현상 표면에 대한 입력 데이터 투표의 각 점을 야기한다.이러한 사인파 표면의 교차점은 평면의 존재를 나타낸다.^[14]3차원 이상에 대한 보다 일반적인 접근방식은 검색 경험의 실현가능성을 유지하도록 요구한다.^[15]

호프 변환은 또한 2단계 접근법을 사용하여 점 구름에서 원통형 물체를 찾는 데 사용되었다.첫 번째 단계는 실린더의 방향을 찾고 두 번째 단계는 위치와 반지름을 찾는다.^[16]

가중 피쳐 사용

하나의 일반적인 변화 세부사항.즉, 한 단계에서 카운트가 가장 높은 빈을 찾아 다음 단계에서 검색된 값의 범위를 제약하는 데 사용할 수 있다.

신중하게 선택한 매개변수 공간

Hough 변환을 위한 고차원 매개변수 공간은 느릴 뿐만 아니라, 사전 검토 없이 구현하면 사용 가능한 메모리를 쉽게 오버런할 수 있다.프로그래밍 환경에서 가상 메모리를 통해 가용 메모리 공간보다 큰 배열을 할당할 수 있다 하더라도, 축전지 배열이 무작위로 액세스되는 방식으로 사용되기 때문에 이에 필요한 페이지 스왑의 수는 매우 까다로울 것이다. 왜냐하면 축전지 배열이 인덱스에서 인덱스로 건너뛰기 때문에 연속 메모리에서는 거의 중단되지 않기 때문이다.

800x600 이미지에서 타원을 찾는 작업을 고려하십시오.타원의 반지름이 주축을 따라 방향을 잡았다고 가정하면 매개변수 공간은 4차원이다.(x,y)는 타원의 중심을 정의하며, a와 b는 두 개의 반지름을 나타낸다.이미지에서 중심을 아무 곳에나 허용하면 제약 조건 0(<800 및 0(<600))이 추가된다.radii에 제약조건과 같은 값이 주어진다면, 남은 것은 2,300억 이상의 값을 희박하게 채운 축열조 배열이다.

따라서 구상된 프로그램은 충분한 메모리를 할당하는 것이 허용되지 않을 것이다.이것은 문제를 해결할 수 없다는 것을 의미하는 것이 아니라 축전지 배열의 크기를 제약하는 새로운 방법만 발견하게 되어 실현가능성이 있다.예를 들어,

1. 타원이 각각 영상에 완전히 포함되어 있다고 가정하는 것이 타당하다면 반지름의 범위를 줄일 수 있다.라디아가 가장 클 수 있는 것은 타원의 중심이 이미지의 중앙에 있는 경우로서 타원의 가장자리가 가장자리까지 늘어나게 한다.이 극단적인 경우, 반지름은 각각 같은 방향으로 향하는 이미지 크기의 절반만 될 수 있다.이러한 방식으로 a와 b의 범위를 줄이면 축전지 배열이 570억 값으로 줄어든다.
2. Hough 변환 추정에서 공간에 대한 트레이드 정확도는 탐지된 가장자리의 모든 픽셀에서 기여를 누적한다.Hough 변환은 탐지된 가장자리에 있는 모든 픽셀의 기여를 누적한다.중심:중심이 x축과 y축 모두에서 3으로 꺼질 것으로 예측되는 경우 이는 축전지 배열의 크기를 약 60억 값으로 감소시킨다.
3. 반지름 추정의 공간에 대한 트레이드 정확도:라디아가 각각 꺼진 것으로 추정되면 축열조 배열 크기를 약 2억 5천 5백만 값 더 줄일 수 있다.
4. 이미지를 관심 영역으로 자르십시오.이것은 이미지에 의존하기 때문에 예측할 수 없지만, 이미지에서 관심 있는 모든 가장자리가 해당 이미지의 왼쪽 상단 사분면에 있는 경우를 상상해 보십시오.축열조 배열은 총 16의 감소계수를 위해 4개의 매개변수 모두를 2의 인수로 구속함으로써 훨씬 더 줄일 수 있다.

이 제약조건들 중 처음 3가지를 에 대해 설명한 예에 적용함으로써 축열조 배열의 크기는 거의 1000배 감소하여 현대 컴퓨터의 메모리에 훨씬 더 잘 맞을 수 있는 크기로 내려온다.

효율적인 타원 검출 알고리즘

용홍희와 치앙지는 기억력 문제를 극복함으로써 타원검출을 위한 허프 변환을 효율적으로 구현할 수 있는 방법을 제시한다.^[17]알고리즘(논문의 2페이지)에서 논의한 바와 같이, 이 접근방식은 영상의 타원을 검출하기 위해 1차원 축전지(부축용)만을 사용한다.영상에서 0이 아닌 점의 수에서 복잡도는 O(N³)이다.

제한 사항

허우 변환은 오른쪽 빈에 높은 득표수가 떨어져야만 효율적이어서 배경 잡음 속에서도 빈을 쉽게 감지할 수 있다.이것은 쓰레기통이 너무 작지 않아야 한다는 것을 의미하거나, 그렇지 않으면 이웃 쓰레기통에서 일부 표가 떨어져서 주 쓰레기통의 가시성이 떨어지게 된다는 것을 의미한다.^[18]

또한 매개변수의 수가 많을 때(즉, 일반적으로 3개 이상의 매개변수로 Hough 변환을 사용할 때), 단일 빈에서 투표하는 평균 득표수는 매우 낮으며, 이미지의 실제 인물에 해당하는 빈은 반드시 이웃보다 훨씬 높은 득표수를 갖는 것으로 보이지는 않는다.The complexity increases at a rate of ${\displaystyle {\mathcal {O}}\left({A^{m-2}}\right)}$ with each additional parameter, where ${\displaystyle A}$ is the size of the image space and ${\displaystyle m}$ is the number of parameters. (Shapiro and Stockman, 310) Thus, the Hough transform must be used선이나 동그라미 이외의 것은 아주 조심스럽게 탐지해 낸다.

마지막으로, Hough 변환의 효율의 대부분은 입력 데이터의 품질에 의존한다. Houg 변환이 효율적이려면 가장자리가 잘 감지되어야 한다.시끄러운 이미지에 Hough 변환을 사용하는 것은 매우 민감한 문제로서 일반적으로, 이전에 디노이즈 단계를 사용해야 한다.레이더 영상의 경우와 마찬가지로 반점에 의해 이미지가 손상되는 경우, 라돈 변환은 합산을 통해 소음을 감쇠시키기 때문에 라돈 변환을 선 검출에 선호하기도 한다.

참고 항목

• 일반화된 Hough 변환
• 무작위화된 Hough 변환
• 라돈 변환
• 푸리에 변환

참조

외부 링크

• hough_transform.cpp – C++ 코드 – CImg 라이브러리(오픈 소스 라이브러리, C++ 소스 코드, 그레이스케일 이미지)의 예
• Hough Transform의 기본에 관한 대화형 시연
• https://web.archive.org/web/20070827233423/http://www.rob.cs.tu-bs.de/content/04-teaching/06-interactive/Hough.html – Java 애플릿 + Hough 변환을 배울 수 있는 슬로프 형태 소스
• https://web.archive.org/web/20070827191440/http://www.rob.cs.tu-bs.de/content/04-teaching/06-interactive/HNF.html – Java 애플릿 + 정상적인 형태의 Hough-Transformation 학습 소스
• http://www.sydlogan.com/deskew.html – Hough 변환을 사용하여 이미지 디스큐(회색 스케일 이미지, C++ 소스 코드)
• https://web.archive.org/web/20070922090216/http://imaging.gmse.net/articledeskew.html – Hough 변환을 사용하여 이미지 디스큐(Visual Basic 소스 코드)
• http://www.mitov.com/products/visionlab – Delphi, C++ 및 .교육용 NET Free Line, Circle 및 Line 세그먼트 Hough 변환 구성요소를 포함하는 라이브러리.
• Tarsha-Kurdi, F, Landes, T, Grussenmeyer, P, 2007a. Lidar 데이터에서 3D 건물 지붕 평면의 자동 탐지를 위한 Hough-transform 및 확장 RANSAC 알고리즘.ISPRS 절차.작업장 레이저 스캔.2007년 9월 12일-14일 핀란드 에스푸.
• Inside에는 C++에서 선형 및 원형 Hough 변환의 오픈 소스 구현이 포함됨
• http://www.vision.ime.usp.br/~edelgado/defesa/code/hough.html C에서 구현된 Ellipse 검출용 Hough-transform.
• Scikit-image Hough-transform for line, circle, circipse, python에서 구현.
• [1] 특정 반지름의 원을 탐지하기 위해 파장 필터링에 기반한 Hough 변환. (Matlab 코드)
• MATLAB를 사용한 선에 대한 Hough 변환
• MATLAB의 원에 대한 Hough 변환
• KHT – C++ 소스 코드.
• 3DKHT – C++ 소스 코드 및 데이터셋.