슈타이니츠 정리

수학의 한 분야인 다면체 조합학에서 슈타이니츠 정리는 3차원 볼록 다면체의 모서리와 꼭짓점에 의해 형성된 무방향 그래프의 특성화입니다. 이들은 정확히 3개의 꼭짓점으로 연결된 평면 그래프입니다. 즉, 모든 볼록 다면체는 3-연결된 평면 그래프를 이루며, 모든 3-연결된 평면 그래프는 볼록 다면체의 그래프로 나타낼 수 있습니다. 이러한 이유로 3개의 연결된 평면 그래프는 다면체 그래프라고도 합니다.^[1]

이 결과는 더 높은 차원에서 알려지지 않은 3차원 볼록 다면체에 대한 분류 정리를 제공합니다.^[2] 이는 이 다면체의 그래프에 대한 완전하고 순수한 조합적 설명을 제공하여 주어진 유형의 면으로 다면체의 구현에 대한 에버하르트의 정리와 같은 다른 결과를 이러한 도형의 기하학적 구조를 참조하지 않고 더 쉽게 증명할 수 있게 해줍니다.^[3] 또한 추상 그래프의 3차원 시각화를 구성하는 방법으로 그래프 그리기에 적용되었습니다.^[4] 브랑코 그ü바움은 이 정리를 "3-폴리토페에 대해 알려진 가장 중요하고 깊은 결과"라고 불렀습니다.

이 정리는 1922년 에른스트 슈타이니츠의 출판물에 등장하며,^[6] 그의 이름을 따서 붙여졌습니다. 수학적 귀납법(슈타이니츠가 그랬던 것처럼), 2차원 스프링 시스템의 최소 에너지 상태를 찾아 결과를 3차원으로 들어 올리거나 원 패킹 정리를 사용하여 증명할 수 있습니다. 주어진 그래프를 실현하는 다면체가 추가적인 제약을 갖는 정리의 몇 가지 확장이 알려져 있습니다. 예를 들어, 모든 다면체 그래프는 정수 좌표를 갖는 볼록 다면체의 그래프이거나, 모든 모서리가 공통 중구에 접하는 볼록 다면체의 그래프입니다.

정리의 정의와 진술

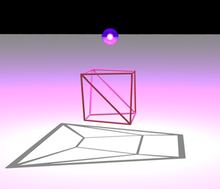
무방향 그래프는 꼭지점과 모서리로 이루어진 시스템으로, 각 모서리는 두 꼭지점을 연결합니다. 그래프 이론에서 흔히 볼 수 있듯이, 슈타이니츠 정리의 목적을 위해 이 그래프들은 유한하고 단순한 것으로 제한됩니다. (같은 두 꼭짓점을 연결하는 두 꼭짓점과 자신을 연결하는 꼭짓점은 없습니다.) 그래프의 꼭짓점이 다면체의 꼭짓점과 일치하도록 하고, 대응하는 두 다면체 꼭짓점이 다면체의 꼭짓점이 될 때마다 어떤 두 그래프 꼭짓점을 한 변으로 연결함으로써 어느 다면체로부터도 그래프를 형성할 수 있습니다. 이 그래프는 다면체의 골격이라고 알려져 있습니다.^[7]

그래프는 유클리드 평면에서 꼭짓점을 점으로 하고, 꼭짓점을 나타내는 점이 꼭짓점이 꼭짓점의 끝점일 때만 꼭짓점을 나타내는 곡선 위에 있도록 이 점들을 연결하는 곡선으로 그릴 수 있는 경우 평면입니다. Farry의 정리에 의해, 모든 평면도는 모서리를 나타내는 곡선이 선분이 되도록 직선화될 수 있습니다. 그래프가 3개 이상의 정점을 가진 경우 3-연결되며, 두 개의 정점을 제거한 후에도 다른 정점 쌍은 경로로 연결된 상태로 유지됩니다. 슈타이니츠의 정리는 이 두 조건이 3차원 볼록 다면체의 골격을 특성화하는 데 필요하고 충분하다는 것을 말합니다: $주어진{\displaystyle }$ 그래프$$G {\$displaystyle$ G$}$는 $G{\displaystyle }$ ${\displaystyle G}$가 평면적이고 3-vertex 연결된 경우에만 볼록한 3차원 다면체의 그래프입니다.^[5][8]

증명

슈타이니츠 정리의 한 방향(증명하기 쉬운 방향)은 모든 볼록 다면체의 그래프가 평면이고 3-연결되어 있다고 말합니다. 그림과 같이 평면성은 슐레겔 다이어그램을 사용하여 나타낼 수 있습니다. 다면체의 한 면 근처에 광원을 배치하고 다른 면에 평면을 배치하면 다면체 가장자리의 그림자가 평면 그래프를 형성하고 가장자리가 직선 세그먼트가 되도록 삽입됩니다. 다면체 그래프의 3-연결은 임의의 $k{\displaystyle }$ ${\displaystyle$ k$}$차원$$ 볼록 폴리토프의 그래프가 $k{\displaystyle }$ ${\displaystyle$ k$}-$연결되어$$ 있다는 발린스키 정리의 특별한 경우입니다. ${\displaystyle \mathrm{정점}}$ 중 k-1${\displaystyle k-1}$개를 제거한 후, 하나의 $정점{\displaystyle }$ v ${\displaystyle$ v$}$를$$더 선택하여 $k{\displaystyle }$ ${\displaystyle$ k$}$개의$$ 정점 집합에서 0인 선형 함수를 찾음으로써 폴리토프의 그래프의 연결성을 증명할 수 있습니다. 심플렉스 방법으로 생성된 경로를 따라 모든 정점을 선형 함수의 두 개의 극단 정점 중 하나에 연결하고 선택한 정점 $v{\displaystyle }$ ${\displaystyle$ v$}$를 양쪽에 연결합니다$$.^[9]

슈타이니츠 정리의 또 다른 좀 더 어려운 방향은 모든 평면 3-연결 그래프는 볼록 다면체의 그래프라는 것입니다. 이 부분에 대한 세 가지 표준 접근법이 있습니다: 유도에 의한 증명, 맥스웰-크레모나 대응을 사용하여 2차원 Tutte 임베딩을 3차원으로 들어올리는 방법, 그리고 원 패킹 정리를 사용하여 표준 다면체를 생성하는 방법.

인덕션

슈타이니츠의 원래 증명은 그래프 이론의 관점에서 표현되지는 않았지만 이러한 용어로 다시 작성될 수 있으며 3-연결된$$ $그래프$를 사면체의 그래프인 $K4$ $displaystyle$ K_{4}}로 줄이는 일련의 δY- 및 Y δ 변환을 찾는 것을 포함합니다. Y δ 변환은 그래프에서 3도 꼭짓점을 제거하고, 해당 꼭짓점이 이미 존재하지 않는 경우 이전의 모든 이웃 사이에 꼭짓점을 추가합니다. 역변환인 δY 변환은 그래프에서 삼각형의 꼭짓점을 제거하고 동일한 3개의 꼭짓점에 인접한 새로운 3도 꼭짓점으로 대체합니다. 그런 수열이 발견되면, 정사면체에서 시작하여 원하는 다면체를 단계적으로 쌓아 올리는 기하학적 연산으로 반전하여 변환할 수 있습니다. 역순의 각 Y δ 변환은 다면체에서 3도 꼭짓점을 잘라냄으로써 기하학적으로 수행할 수 있습니다. 반대 순서의 δY-변환은 다면체에서 삼각형 면을 제거하고 이웃 면을 만나는 지점까지 확장하여 기하학적으로 수행할 수 있지만, 이웃한 면 3개의 삼중 교차점이 다면체에서 제거된 면의 먼 쪽에 있을 때만 수행됩니다. 삼중 교점이 이 면의 먼 쪽에 있지 않을 때, 다면체의 투영 변환은 그것을 올바른 쪽으로 이동시키기에 충분합니다. 따라서$$ $그래프를 K4$ $displaystyle$ K_{4}}로 줄이기 위해 필요한 δY- 및 Y δ-변환의 수를 유도하면 모든 다면체 그래프를 다면체로 구현할 수 있습니다.

에피파노프의 이후 연구는 모든 다면체 그래프가 δY- 및 Y δ 변환에 의해 ${\displaystyle {K4}_{}}$ ${\displaystyle K_{4}}$로 축소될 수 있다는 슈타이니츠의 증명을 강화했습니다. Epifanov는 평면 그래프에 두 개의 정점이 지정되면 직렬-병렬 감소와 함께 δY- 및 Y δ-변환을 결합함으로써 그래프를 해당 단자 사이의 단일 에지로 축소할 수 있음을 증명했습니다. 에피파노프의 증명은 복잡하고 비구조적이었지만 트루엠퍼는 그래프 마이너를 기반으로 한 방법을 사용하여 단순화했습니다. Trueemper는 이러한 방식으로 모든 그리드 그래프가 δY- 및 Y δ- 변환에 의해 축소 가능하며, 이러한 축소성은 그래프 부차적으로 유지되며, 모든 평면 그래프는 그리드 그래프의 부차적임을 관찰했습니다. 이 아이디어는 환원 순서가 존재한다는 슈타이니츠의 보조정리를 대체하는 데 사용될 수 있습니다. 이 교체 후 나머지 증명은 Steinitz의 원래 증명과 동일한 방법으로 귀납법을 사용하여 수행할 수 있습니다.^[8] δY- 및 Y δ-변환의 시퀀스를 찾는 방법 중 하나를 사용하여 수행된 이러한 증명의 경우 비선형적인 단계 수를 필요로 하는 다면체 그래프가 있습니다. 보다 정확하게 말하면, 모든 평면 그래프는 n ${\displaystyle {3\mathrm{}}^{}}$ /${\displaystyle {2\mathrm{}}^{}}$ ${\$ $n$$^{3/2}}$에 비례하는 여러 단계를 사용하여 축소할 수 있으며$,$ 무한히 많은 그래프는 n ${\displaystyle {3\mathrm{}}^{}}$/ 2 ${\$ n$^{3/2}$에 적어도 비례하는 여러 단계를 필요로 합니다$.$ 여기서 $n{\displaystyle }$ ${\displaystyle n}$은 그래프의 정점 수이 됩니다.^[12][13]

다른 형태의 귀납 증명은 간선을 제거하거나(그리고 이 제거 후에 남을 수 있는 2개의 정점을 압축하여) 간선을 수축하고 주어진 평면 그래프의 부차적인 형태를 형성하는 것에 기초합니다. 모든 다면체 그래프는 이러한 연산을 선형적으로$$ ${\displaystyle {수행}_{}}$하여 K 4$${\$displaystyle K_{4}}$로 축소할 수 있으며, 다시 연산을 반전하고 기하학적으로 수행하여 그래프의 다면체를 구현할 수 있습니다. 그러나 이 유형의 논법에 대해 축소 시퀀스가 존재한다는 것을 증명하는 것이 더 쉽고 축소 시퀀스가 더 짧지만, 시퀀스를 역전시키는 데 필요한 기하학적 단계는 더 복잡합니다.^[14]

리프팅

직선 모서리가 있는 평면에 그래프가 그려진 경우, 균형 응력은 0이 아닌 실수(가중치)를 모서리에 할당하는 것으로 정의되며, 각 정점은 이웃의 가중 평균에 의해 주어진 위치에 있습니다. 맥스웰-크레모나 대응에 따르면, 평형 응력은 표면의 평평한 부분들 사이의 경계들을 형성하는 가장자리들이 주어진 도면에 투영되도록 조각들로 이루어진 선형 연속적인 3차원 표면으로 들어올릴 수 있습니다. 각 모서리의 무게와 길이는 모서리의 양쪽 표면의 기울기 차이를 결정하며, 각 꼭짓점이 이웃과 평형을 이룬다는 조건은 이러한 기울기 차이로 인해 표면이 꼭짓점 근처에서 자신과 올바르게 일치한다는 조건과 같습니다. 양의 가중치는 조각별 선형 표면의 두 면 사이의 볼록한 정이면체 각도로, 음의 가중치는 오목한 정이면체 각도로 해석됩니다. 반대로, 모든 연속적인 조각별 선형 표면은 이러한 방식으로 평형 응력에서 비롯됩니다. 그림의 모든 내부 모서리가 양의 가중치를 가지며, 모든 외부 모서리가 음의 가중치를 갖는 방식으로 유한 평면 그래프를 그리고 평형 응력을 부여한다면, 이러한 방식으로 이 응력을 3차원 표면으로 변환함으로써, 그래프의 외부를 나타내는 평면을 같은 평면에서의 보형물로 대체하면 평면에 대한 수직 투영이 교차를 갖지 않는다는 추가적인 특성을 갖는 볼록 다면체를 얻을 수 있습니다.^[15][16]

Maxwell-Cremona 대응은 Tutte 임베딩인 W. T. Tutte의 평면 그래프 그리기 방법과 결합하여 다면체 그래프의 다면체 구현을 얻는 데 사용되었습니다. Tutte의 방법은 다면체 그래프의 한 면을 평면에서 볼록한 위치로 고정하는 것으로 시작됩니다. 이 면은 그래프 도면의 외부 면이 됩니다. 이 방법은 각 나머지 정점이 이웃의 평균에 배치되어야 하는 정점 좌표에 선형 방정식 시스템을 설정함으로써 계속됩니다. 그러면 Tutte가 보여준 것처럼, 이 방정식 체계는 그래프의 각 면이 볼록 다각형으로 그려진 독특한 해를 가질 것입니다.^[17] 직관적으로 이 솔루션은 그래프의 내부 가장자리를 이상적인 스프링으로 대체하고 최소 에너지 상태로 정착시켜 얻을 수 있는 패턴을 설명합니다.^[18] 결과는 거의 평형 스트레스입니다. 각 내부 모서리에 가중치를 하나씩 할당하면 도면의 각 내부 꼭지점이 평형 상태에 있습니다. 그러나 항상 외부 모서리에 음수를 할당하여 균형을 이룰 수 있는 것은 아닙니다. 이러한 할당은 외부 면이 삼각형일 때 항상 가능하므로 이 방법을 사용하여 삼각형 면을 갖는 다면체 그래프를 구현할 수 있습니다. 다면체 그래프가 삼각형 면을 포함하지 않는 경우, 이중 그래프는 삼각형을 포함하고 또한 다면체이므로 이러한 방법으로 이중을 실현한 다음 원래의 그래프를 이중 실현의 극성 다면체로 실현할 수 있습니다.^[4][19] 리프팅을 사용하여 다면체를 구현하기 위한 대안적인 방법은 최대 5개의 꼭짓점을 가진 모든 면을 외부 면으로 선택하여 이중성을 방지합니다. 모든 다면체 그래프는 그러한 면을 가지고 있으며, 이 면의 고정된 모양을 더 신중하게 선택함으로써 나머지 그래프의 투테 임베딩을 들어 올릴 수 있습니다.^[20]

원형포장

원 채우기 정리의 한 변형에 따르면, 모든 다면체 그래프에 대해, 평면 또는 임의의 구에 그래프의 꼭짓점과 면을 나타내는 원들의 체계가 존재하므로 다음과 같습니다.

• 그래프의 인접한 두 꼭짓점은 각각 접선원으로 표시됩니다.
• 그래프의 인접한 두 면은 각각 접선원으로 표시됩니다.
• 꼭짓점과 그것이 닿는 면의 각 쌍은 직각으로 교차하는 원으로 표현되며,
• 다른 모든 쌍의 원들은 서로 분리되어 있습니다.^[21]

동일한 원 시스템은 정점을 나타내는 원과 얼굴을 나타내는 원의 역할을 교환하여 이중 그래프의 표현을 형성합니다. 3차원 유클리드 공간에 내장된 구면에 대한 이러한 표현으로부터, 경계가 면 원을 통과하는 반 공간의 교차점으로서 주어진 그래프와 조합적으로 동등한 볼록 다면체를 형성할 수 있습니다. 이 다면체의 각 꼭짓점에서 보면, 그 꼭짓점에서 보이는 구 위의 지평선이 바로 그것을 나타내는 원입니다. 이 지평선 속성은 각 정점의 3차원 위치를 결정하며, 다면체는 이와 같이 위치한 정점의 볼록한 선체로 동등하게 정의될 수 있습니다. 구체는 실현의 중심이 됩니다: 다면체의 각 가장자리는 두 개의 접선 꼭짓점 원이 두 개의 접선 면 원과 교차하는 지점에서 구와 접선입니다.^[22]

추가 속성을 사용한 실현

정수좌표

모든 다면체 그래프는 좌표가 정수인 볼록 다면체에 의해 실현될 수 있다는 슈타이니츠 정리의 더 강력한 형태를 증명할 수 있습니다.^[23] 예를 들어, 슈타이니츠의 원래 유도 기반 증명은 이런 방식으로 강화될 수 있습니다. 그러나 슈타이니츠의 구성에서 얻을 수 있는 정수는 주어진 다면체 그래프의 꼭짓점 수에서 두 배 지수입니다. 이 크기의 숫자를 이진법으로 적으려면 기하급수적으로 많은 비트가 필요합니다.^[19] 기하학적으로, 이것은 다면체의 일부 특징이 다른 특징보다 기하학적으로 두 배 더 큰 크기를 가질 수 있다는 것을 의미하며, 이 방법에서 도출된 실현은 그래프 그리기에 적용하기에 문제가 있습니다.^[4]

후속 연구자들은 정점당 선형 수의 비트만을 사용하는 리프팅 기반 실현 알고리즘을 발견했습니다.^[20][24] 또한 좌표가 정수여야 한다는 요구를 완화하고 정점의 $x{\displaystyle }$ ${\displaystyle x}$ 좌표가$$ 0~${\displaystyle 2}$ n${\displaystyle }$- ${\displaystyle 4}$ ${\displaystyle 2n-4}$ 범위의 서로 다른 정수이고$$ 나머지 두 좌표가 단위 간격의 실수인 방식으로 좌표를 할당할 수 있습니다. 각 모서리의 길이가 적어도 하나이고 전체 다면체의 부피가 선형이 되도록 합니다.^[25][26] 일부 다면체 그래프는 다항식 크기의 그리드에서만 실현 가능한 것으로 알려져 있으며, 특히 피라미드(휠 그래프의 실현), 프리즘(프리즘 그래프의 실현) 및 적층 다면체(아폴로니아 네트워크의 실현)에 해당됩니다.^[27]

정수 구현의 존재를 나타내는 또 다른 방법은 모든 3차원 볼록 다면체가 조합적으로 동등한 정수 다면체를 갖는다는 것입니다.^[23] 예를 들어, 정십이면체는 정십면체의 오각형 면 때문에 그 자체가 정수 다면체는 아니지만, 동등한 정수 다면체로 구현될 수 있습니다.^[20] 높은 차원에서 정수에 해당하지 않는 폴리토프(예: Perles 구성에서 구성된 폴리토프)가 존재하는 경우에는 항상 이러한 작업이 가능하지 않습니다.^[28]

등경사

할린 그래프(Halin graph)는 다면체 그래프의 특별한 경우로, 나무의 잎을 사이클로 연결하여 평면에 포함된 트리(도 2개의 꼭짓점이 없는)로부터 형성됩니다. Halin 그래프의 경우 특별한 유형의 다면체 구현을 선택할 수 있습니다: 외부 주기는 수평 볼록 기본 면을 형성하고 다른 모든 면은 기본 면 바로 위에 있으며(양력을 통해 실현된 다면체에서와 같이), 이 모든 상부 면은 동일한 기울기를 가지고 있습니다. 모든 기본 다각형 위에 동일한 기울기의 면을 갖는 다면체 표면은 다각형의 직선 골격으로 구성할 수 있으며, 이와 동등한 방법은 기본 면에 대한 나무의 2차원 투영이 직선 골격을 형성한다는 것입니다. 이 결과의 증명은 귀납법을 사용합니다: 어떤 뿌리가 있는 나무라도 자식이 모두 잎인 내부 노드에서 잎을 제거함으로써 더 작은 나무로 축소될 수 있습니다. 더 작은 나무에서 형성된 Halin 그래프는 귀납 가설에 의해 실현됩니다. 그리고 자식이 제거된 트리 노드에 임의 수의 리프 자식을 추가하기 위해 이 인식을 수정하는 것이 가능합니다.^[29]

얼굴 모양 지정

주어진 다면체 $그래프{\displaystyle }$ G ${\displaystyle$ $G$$}$를 나타내는 임의의 다면체에서$,$ $G{\displaystyle }$ ${\displaystyle$ G$}$의 면은 G ${\displaystyle$ G}를 두 성분으로$$ 분리하지 않는$$ G ${\displaystyle G}$의 $사이클$과 정확히$$ 일치합니다: 즉, $G{\displaystyle }$ ${\displaystyle G}$에서 얼굴 주기를 제거하면 $G{\displaystyle }$ ${\displaystyle G}$의 나머지 부분이 연결된 하위 그래프로$$ 남습니다$$. 그러한 주기를 주변 주기라고 합니다. 따라서 면의 조합 구조(기하학적 모양은 아님)는 그래프 구조에서 고유하게 결정됩니다. Barnette와 Grünbaum에 의한 Steinitz 정리의 또 다른 강화는 임의의 다면체 그래프, 그래프의 임의의 면 및 그 면을 나타내는 임의의 볼록 다각형에 대하여, 지정된 면에 대하여 지정된 모양을 갖는 전체 그래프의 다면체 구현을 찾는 것이 가능하다는 것을 말합니다. 이것은 모든 다면체 그래프가 모든 면이 볼록하고 외부 면에 대해 지정된 모양으로 평면에 그려질 수 있다는 Tutte의 정리와 관련이 있습니다. 그러나 Tutte의 방법으로 생성된 평면 그래프 도면이 반드시 볼록 다면체로 상승하는 것은 아닙니다. 대신에 Barnette와 Grünbum은 귀납적 방법을 사용하여 이 결과를 증명합니다.^[30] 또한 다면체 그래프 $G{\displaystyle }$ ${\displaystyle$ $G$$}$와 $G{\displaystyle }$ ${\displaystyle$ $G$$}$의 임의의 $사이클{\displaystyle }$ C ${\displaystyle$ C$}$가 주어지면$$$C{\displaystyle }$ ${\displaystyle$ C$}$가 평행 투영 하에서 구현의 실루엣을 형성하는$$ 구현을 찾는 것이 항상 가능합니다.^[31]

접선 구

원 패킹 정리를 사용한 다면체의 실현은 슈타이니츠 정리의 또 다른 강화를 제공합니다: 모든 3개의 연결된 평면 그래프는 모든 가장자리가 다면체의 중간 구인 동일한 단위 구에 접하도록 볼록 다면체로 표현될 수 있습니다.^[22] 원 패킹을 다면체로 변환하기 전에 신중하게 선택된 뫼비우스 변환을 수행함으로써 모든 그래프 오토모피즘이 다면체 구현의 대칭이라는 의미에서 기본 그래프의 모든 대칭을 실현하는 다면체 구현을 찾을 수 있습니다.^[32][33] 보다 일반적으로, $G{\displaystyle }$ ${\displaystyle$ G$}$가 다면체 그래프이고 $K{\displaystyle }$ ${\displaystyle$ K$}$가 임의의 매끄러운 3차원 볼록체인 경우, 모든 간선이$$ K ${\displaystyle K}$에 접하는 $G{\displaystyle }$ ${\displaystyle G}$의 다면체 표현을 찾을 수 있습니다$.$^[34]

원 패킹 방법을 사용하여 모든 꼭짓점에 걸쳐 원구 또는 모든 면에 접하는 내구를 갖는 다면체의 그래프를 특성화할 수도 있습니다. (원구가 있는 다면체는 쌍곡 기하학에서도 이상적인 다면체로서 중요합니다.) 두 경우 모두 구의 존재는 그래프의 각 모서리와 관련된 양의 실제 변수에 대한 선형 부등식 시스템의 용해도와 같습니다. 지표면의 경우 이러한 변수는 그래프의 각 얼굴 주기에서 정확히 1개로, 각 얼굴이 아닌 주기에서 1개 이상으로 합산되어야 합니다. 이중으로, 원근의 경우 변수는 각 정점에서 하나씩, 절단의 양쪽에 둘 이상의 정점이 있는 각 절단에 걸쳐 하나 이상의 변수를 합산해야 합니다. 만족해야 할 선형 부등식이 기하급수적으로 많을 수 있지만, 타원체 방법을 사용하여 다항식 시간 내에 해를 찾을 수 있습니다. 해의 변수 값은 해당 다면체가 구면과 원하는 관계를 갖는 원 패킹의 원 쌍 사이의 각도를 결정합니다.^[35][36]

관련결과

3보다 높은 차원에서 알고리즘 슈타이니츠 문제는 주어진 격자가 볼록 폴리토프의 면 격자인지 여부를 결정하는 것으로 구성됩니다. 리히터-게버트의 보편성 정리에 의해 4차원 폴리토프의 경우에도 NP가 단단하고 실제의 실존 이론에 대해 더 강력하게 완전하기 때문에 다항식 시간 복잡성을 가질 가능성은 거의 없습니다.^[38] 여기서 실수의 실존 이론은 다항식과 부등식의 주어진 체계를 만족하는 실수 변수를 찾는 측면에서 공식화될 수 있는 계산 문제의 한 종류입니다. 알고리즘 슈타이니츠 문제의 경우 그러한 문제의 변수는 폴리토프의 꼭짓점 좌표가 될 수 있으며 방정식과 부등식을 사용하여 주어진 면 격자에서 각 면의 평탄도와 면 사이 각의 볼록도를 지정할 수 있습니다. 완전성은 이 클래스의 다른 모든 문제가 다항식 시간 내에 알고리즘 슈타이니츠 문제의 동등한 인스턴스로 변환될 수 있음을 의미합니다. 이러한 변환의 존재는 알고리즘 슈타이니츠 문제가 다항 시간 해를 가지고 있다면, 현실의 실존 이론의 모든 문제와 NP의 모든 문제가 마찬가지라는 것을 의미합니다.^[39] 그러나 주어진 그래프는 두 개 이상의 면 격자에 대응할 수 있기 때문에 이 완전성 결과를 4-폴리토페의 그래프를 인식하는 문제로 확장하기는 어렵습니다. 이 그래프 인식 문제의 계산 복잡성을 결정하는 것은 여전히 열려 있습니다.^[40]

연구원들은 또한 3차원 비볼록 다면체와^[37][41] 4차원 볼록 다면체의 특정한 특별한 부류의 그래프의 그래프 이론적 특성을 발견했습니다.^[40][42][43] 그러나 두 경우 모두 일반적인 문제는 해결되지 않은 채로 남아 있습니다. 실제로, 어떤 완전한 그래프가 (사면체의 경우$$ $K{\displaystyle {}_{}}$ ${\displaystyle {4\mathrm{}}_{}}$ ${\$ Császar 다면체의 경우$$ $K{\displaystyle {}_{}}$ ${\displaystyle {7\mathrm{}}_{}}$ ${\$ 제외)의 그래프인지를 결정하는 문제도 해결되지 않은 채 남아 있습니다.^[44]

에버하르트의 정리는 볼록 다면체의 면을 형성하기 위해 결합될 수 있는 다각형의 다중집합을 부분적으로 특징짓습니다. 주어진 다각형 면들의 집합으로 3-연결된 평면 그래프를 형성한 다음 슈타이니츠 정리를 적용하여 해당 그래프의 다면체 구현을 찾음으로써 증명할 수 있습니다.^[3]

László Lovász는 그래프의 다면체 표현과 동일한 그래프의 콜린 드 베르디에르 그래프 불변량을 실현하는 행렬 사이의 대응 관계를 보여주었습니다. 콜린 드 베르디에르 불변량은 다면체 그래프와 무관한 몇 가지 추가 조건에서 그래프의 가중 인접 행렬의 최대 코랭크입니다. These are square symmetric matrices indexed by the vertices, with the weight of vertex ${\displaystyle i}$ in the diagonal coefficient ${\displaystyle M_{i,i}}$ and with the weight of edge ${\displaystyle i,j}$ in the off-diagonal coefficients ${\displaystyle M_{i,j}}$ and ${\displaystyle M_{j,}}$${\displaystyle i_{}}$ ${\$ $정점{\displaystyle }$ i ${\displaystyle$ $i$$}$와 $j{\displaystyle }$ ${\displaystyle$ j$}$가 인접하지 않을 때 계수 ${\displaystyle {Mi,}_{}}$ ${\displaystyle j_{}}$ ${\$는 0이어야 합니다$$. 이 불변량은 그래프가 평면 그래프인 경우에만 최대 3입니다. Lovász가 보여주는 것처럼 그래프가 다면체일 때, 코랭크 3의 가중 인접 행렬을 찾고, 그 널스페이스의 기초를 형성하는 3개의 벡터를 찾고, 이 벡터의 계수를 다면체의 꼭짓점에 대한 좌표로 사용하고, 이 꼭짓점을 적절하게 스케일링하면 다면체로서의 표현을 얻을 수 있습니다.^[45]

역사

슈타이니츠 정리의 역사는 그ü바움(Grünbum, 2007)에 의해 기술되는데, 그는 1916년에 처음으로 쓰여진 에른스트 슈타이니츠의 출판물에서 처음으로 비밀스러운 형태로 등장했다고 언급합니다. 슈타이니츠는 1928년 사망 후에 출판된 강의 노트에서 더 자세한 내용을 제공했습니다. 슈타이니츠 정리의 현대적 처리는 다면체의 그래프 이론적 특성으로 명시하지만 슈타이니츠는 그래프 언어를 사용하지 않았습니다.^[46] 이 정리의 그래프 이론적 공식은 1960년대 초 Branko Grünbum과 Theodore Motzkin에 의해 소개되었으며, 그 증명은 Grünbum의 1967년 텍스트 볼록 폴리토페스에서도 그래프 이론으로 변환되었습니다.^[46] 슈타이니츠의 증명을 강화하는 δY-와 Y δ-변환에 대한 에피파노프의 작업은 다면체의 특성화 이외에 다른 문제들에 의해 동기부여를 받았습니다. Truemper(1989)는 Steinitz의 정리에 대한 이 작업의 관련성을 관찰한 공로를 Grünbum에게 돌립니다.^[11]

응력도형과 다면체 들뜸 사이의 맥스웰-크레모나 대응은 피에르 바리뇽, 윌리엄 랭킨 등의 초기 연구에 기초하여 1864년부터 1870년까지 제임스 클러크 맥스웰에 의해 일련의 논문에서 개발되었으며, 19세기 후반 루이지 크레모나에 의해 대중화되었습니다.^[47] 이 대응이 슈타이니츠의 정리를 증명하기 위해 투테 임베딩과 함께 사용될 수 있다는 관찰은 Eades & Garvan(1995)^[4]에서 비롯됩니다. Richter-Gebert(1996)도 참조하십시오.^[38]

원 채우기 정리는 1936년^[48][49] 폴 쾨베에 의해, 1970년 E. M. 안드레예프에 의해 (독립적으로) 증명되었고,^[49][50] 1980년대 중반에 윌리엄 서스턴에 의해 대중화되었는데, 그는 쾨베와 안드레예프를 인용했음에도 불구하고) 발견자 중 한 명으로 종종 인정받습니다.^[49] 안드레프의 정리 버전은 쌍곡 공간의 특정 다면체에 대한 슈타이니츠와 같은 특성으로 이미 공식화되었으며,^[50] 중구로 다면체를 구현하기 위한 원 패킹의 사용은 서스턴의 연구에서 비롯됩니다.^[51] 내접 또는 외접 구를 갖는 다면체를 특성화하는 문제, 결국 원 패킹 구현에 기초한 방법을 사용하여 해결된 것, 1630년경^[52] 르네 데카르트와 1832년 야콥 슈타이너의 미발표 작품으로 거슬러 올라갑니다;^[35][53] 외피나 외피로 실현되지 않은 다면체의 첫 번째 예는 1928년 슈타이니츠에 의해 주어졌습니다.^[35][54]

참고문헌