주변 사이클
Peripheral cycle그래프 이론에서, 비방향 그래프의 주변 사이클(또는 주변 회로)은 직관적으로 그래프의 어떤 부분도 다른 부분으로부터 분리되지 않는 사이클이다.주변 주기(또는 처음에 불렸던 것처럼, Tutte가 "폴리곤"이라고 불렀기 때문에 주변 다각형은 Tutte(1963년)에 의해 처음 연구되었고 평면 그래프의 특성화와 비 평면 그래프의 주기 공간을 생성하는 데 중요한 역할을 한다.[1]
정의들
그래프 의 주변 주기 은(는) 몇 가지 동등한 방법 중 하나로 공식적으로 정의될 수 있다.
- 이(가) 연결된 그래프의 단순한 사이클이고, 이 속성은 G }, e G\의 두 마다 e로 시작하는 가 경우 1}, }}로 끝나며, {\C[2]에 속하는 내부 정점이 없다.
- 의 가장자리와 꼭지점을 삭제하여 형성된 하위그래프 C G이(가) 연결된 속성과 유도 사이클인 경우 C {\ C은 주변적이다.[3]
- G{G\displaystyle}의 C{C\displaystyle}에서 edge-disjoint G{G\displaystyle}, C{C\displaystyle}의 bridge[4]의 만약 C{C\displaystyle}은 부분 그래프. 미미한 부분 그래프 B{B\displaystyle}과 그 속성은 모든 부착물의 포인트(vertices다 가장자리에 인접해. 에서 및 B C C}에 속하며[5] 다리가 하나만 있으면 간단한 C 이(가) 주변적이다.[6]
이러한 정의의 등가성은 보기 어렵지 않다: G 의 연결된 하위 그래프( 에 연결하는 가장자리와 함께) 또는 유도되지 않는 주기의 화음은 어느 경우든 브리지여야 하며, 또한 2진 관계에서 동등성 등급이어야 한다. 에서 내부 정점이 없는 경로의 끝인 경우 두 가장자리가 연관되어 있는 가장자리[7]
특성.
주변 주기는 다면 그래프 이론, 즉 3-Vertex로 연결된 평면 그래프에 나타난다.모든 평면 그래프 및 의 평면 내장에 대해 유도 사이클인 내장면의 면은 주변 사이클이어야 한다다면 그래프에서 모든 얼굴은 말초적인 순환이며, 모든 말초적인 순환은 얼굴이다.[8]모든 다면 그래프는 (결합 동등성, 외부 표면의 선택, 면의 방향까지) 독특한 평면 내장을 가지고 있다.[9]
평면 그래프에서 사이클 공간은 면에 의해 생성되지만, 비 평면 그래프에서 말초 사이클은 유사한 역할을 한다: 3VERx로 연결된 모든 유한 그래프에 대해 사이클 공간은 말초 사이클에 의해 생성된다.[10]결과는 또한 로컬에서 마무리되지만 무한 그래프까지 확장될 수 있다.[11]특히 3개 연결 그래프에 주변 주기가 포함될 것으로 보장된 데 따른 것이다.주변 주기를 포함하지 않는 2개의 연결 그래프가 존재하지만(예: 모든 사이클에 2개의 브리지가 있는 한 양분 그래프 ,4 2개의 연결 그래프가 최소 3도인 경우 최소 1개의 주변 사이클을 포함한다.[12]
3개의 연결 그래프의 주변 주기는 선형 시간으로 계산할 수 있으며 평면성 테스트를 설계하는 데 사용되어 왔다.[13]그들은 또한 분리되지 않은 귀 분해에 대한 보다 일반적인 개념으로 확장되었다.그래프의 평면성을 테스트하는 일부 알고리즘에서는 문제를 더 작은 하위 문제로 분할하기 위해 주변적이지 않은 주기를 찾는 것이 유용하다.회로 등급이 3 미만(사이클 그래프 또는 세타 그래프 등)인 2연속 그래프에서는 모든 사이클이 주변적이지만 회로 등급이 3 이상인 모든 2연속 그래프는 주변 주기가 아니며, 이는 선형 시간 내에 발견될 수 있다.[14]
시모어&위버(1984)는 코드 그래프를 일반화하면서 모든 주변 주기가 삼각형인 그래프라고 정의한다.그들은 이 그래프를 현악 그래프와 최대 평면 그래프의 총합으로 특징짓는다.[15]
관련개념
로 그것은 또한 2가지지만 뚜렷한 관련 개념들이 있다:그런 사이클이 함께를 삭감하는 것을 표면 연결을 끊지 않을 것의 제거는 접속 형태적으로 포함된 그래프의 나머지 graph,[16]과 사이클을 떼어 낼 것 단순한 사이클 동안 사용되어 왔다 주변 사이클도 하지만 이 용어는 모호하지만,non-separating cycles,[2]으로 불려 왔다. 는 하루에 500파운드그의 그래프는 내장되어 있다.[17]
매트로이드에서 비분리 회로는 회로를 삭제하면 연결된 작은 매트로이드(즉, 매트로이드의 직접적인 합으로 쓸 수 없는)가 남도록 매트로이드(즉, 최소 종속 집합)의 회로다.[18]이것들은 주변 사이클과 유사하지만, 그래픽 매트로이드(회로가 그래프의 단순한 사이클인 매트로이드)에서도 같지 않다.예를 들어 완전한 양분 그래프 , 에서모든 사이클은 주변(하나의 브리지, 두 개의 에지 경로만 있음)이지만 이 브리지에 의해 형성된 그래픽 매트로이드는 연결되지 않아 K , 3 의 그래픽 매트로이드의 회로는 분리되지 않는다.
참조
- ^ Tutte, W. T. (1963), "How to draw a graph", Proceedings of the London Mathematical Society, Third Series, 13: 743–767, doi:10.1112/plms/s3-13.1.743, MR 0158387.
- ^ a b Di Battista, Giuseppe; Eades, Peter; Tamassia, Roberto; Tollis, Ioannis G. (1998), Graph Drawing: Algorithms for the Visualization of Graphs, Prentice Hall, pp. 74–75, ISBN 978-0-13-301615-4.
- ^ 이것은 본질적으로 브루언(2004)이 사용한 정의다.그러나 Bruhn은 이(가) 을C {\의 제거로 인한 연결 해제로부터 분리시킨 경우를 구분한다
- ^ 다른 개념인 브리지(그래프 이론)와 혼동해서는 안 된다.
- ^ Tutte, W. T. (1960), "Convex representations of graphs", Proceedings of the London Mathematical Society, Third Series, 10: 304–320, doi:10.1112/plms/s3-10.1.304, MR 0114774.
- ^ 이것은 투테(1963년)가 원래 사용하던 주변기기의 정의다.세이모어 & 위버(1984)는 주변 주기의 정의는 동일하지만 주변 주기의 유도 사이클 정의와 더 밀접하게 유사한 교량의 정의는 다르다.
- ^ 예: 참조Tutte(1960)의 정리 2.4는 교량의 꼭지점 집합이 경로로 연결되어 있음을 보여주며, 화음 및 연결된 구성요소를 사용한 교량의 정의는 Symour & Weaver(1984)를 참조하고, 가장자리에 있는 이항 관계의 동등성 등급을 사용한 교량의 정의는 Di Battista 등(1998)을 참조한다.
- ^ 투테(1963년), 이론 2.7과 2.8.
- ^ 투테(1963년)의 정리 2.8 다음에 나오는 발언을 참조한다.Tutte가 관찰한 바와 같이, 이것은 이미 알려진 바였다.
- ^ 투테(1963년), 정리 2.5.
- ^ Bruhn, Henning (2004), "The cycle space of a 3-connected locally finite graph is generated by its finite and infinite peripheral circuits", Journal of Combinatorial Theory, Series B, 92 (2): 235–256, doi:10.1016/j.jctb.2004.03.005, MR 2099143.
- ^ Thomassen, Carsten; Toft, Bjarne (1981), "Non-separating induced cycles in graphs", Journal of Combinatorial Theory, Series B, 31 (2): 199–224, doi:10.1016/S0095-8956(81)80025-1, MR 0630983.
- ^ Schmidt, Jens M. (2014), "The Mondshein Sequence", Proceedings of the 41st International Colloquium on Automata, Languages and Programming (ICALP'14), Lecture Notes in Computer Science, vol. 8572, pp. 967–978, doi:10.1007/978-3-662-43948-7_80, ISBN 978-3-662-43947-0.
- ^ Di Battista 외 연구진(1998), Lemma 3.4, 페이지 75–76.
- ^ Seymour, P. D.; Weaver, R. W. (1984), "A generalization of chordal graphs", Journal of Graph Theory, 8 (2): 241–251, doi:10.1002/jgt.3190080206, MR 0742878.
- ^ 예: 참조.
- ^ 예: 참조.
- ^ Maia, Bráulio, Junior; Lemos, Manoel; Melo, Tereza R. B. (2007), "Non-separating circuits and cocircuits in matroids", Combinatorics, complexity, and chance, Oxford Lecture Ser. Math. Appl., vol. 34, Oxford: Oxford Univ. Press, pp. 162–171, doi:10.1093/acprof:oso/9780198571278.003.0010, MR 2314567.
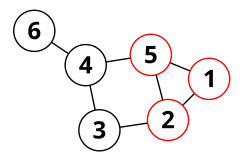
 주변 주기
주변 주기 
 (가)
(가) 
 두
두 



