생물학적 뉴런 모델

급상승 뉴런 ^[1]모델로도 알려진 생물학적 뉴런 모델은 활동 전위 또는 스파이크라고 불리는 세포막 전체에 걸쳐 날카로운 전위를 생성하는 신경계의 특정 세포의 특성에 대한 수학적인 설명입니다.스파이크는 축삭을 따라 전달되고 시냅스는 보내는 뉴런에서 다른 많은 뉴런으로 전달되기 때문에 스파이크 뉴런은 신경계의 주요 정보처리 장치로 여겨진다.스파이킹 뉴런 모델은 다른 범주로 나눌 수 있습니다: 가장 상세한 수학적 모델은 입력 전류와 이온 채널의 활성화의 함수로서 막 전압을 설명하는 생물 물리 뉴런 모델입니다.수학적으로 간단한 것은 입력전류의 함수로서 막전압을 설명하고 활동전위의 시간경로를 형성하는 생물물리 프로세스를 설명하지 않고 스파이크 시간을 예측하는 적분 및 화재 모델입니다.더 추상적인 모델은 자극이 감각 입력을 통해 또는 약리학적으로 발생할 수 있는 자극의 함수로서 출력 스파이크(막 전압이 아님)만 예측한다.이 기사는 가능한 한 다양한 스파이킹 뉴런 모델과 실험 현상에 대한 링크에 대한 간략한 개요를 제공한다.여기에는 결정론적 및 확률론적 모델이 포함된다.

개요:뉴런 모델의 생물학적 배경, 분류 및 목적

비스파이킹 셀, 스파이킹 셀 및 그 측정

신경계의 모든 세포들이 스파이크 뉴런 모델의 범위를 정의하는 스파이크 형태의 스파이크를 생성하는 것은 아닙니다.예를 들어 달팽이관모세포, 망막수용체세포, 망막양극세포는 급증하지 않는다.게다가 신경계의 많은 세포들은 뉴런으로 분류되지 않고 오히려 글루아로 분류된다.

뉴런의 활동은 단일 뉴런의 스파이크 활동을 포착하고 최대 진폭 활동 전위를 생성하는 "전체 세포" 측정 기술과 같은 다른 실험 기술로 측정될 수 있습니다.

세포외 측정 기술을 사용하면 전극(또는 여러 전극의 배열)이 세포외 공간에 배치됩니다.종종 전극의 크기와 선원에 대한 근접성에 따라 여러 스파이킹 선원에서 발생하는 스파이크는 신호 처리 기술로 식별할 수 있습니다.세포외 측정에는 여러 가지 장점이 있습니다. 1) 실험적으로 얻기 쉽고 2) 견고하며 더 오래 지속되며 3) 특히 유사한 세포가 많은 해부학적 영역에서 수행될 때 지배적인 효과를 반영할 수 있습니다.

뉴런 모델의 개요

뉴런 모델은 모델 인터페이스의 물리적 단위에 따라 두 가지 범주로 나눌 수 있습니다.각 카테고리는 추상화/상세 수준에 따라 더 세분화할 수 있습니다.

1. 전기 입력-출력 막 전압 모델 – 이러한 모델은 전류 또는 전압 입력으로 주어진 전기 자극의 함수로서 막 출력 전압을 예측합니다.이 범주의 다양한 모델은 입력 전류와 출력 전압 사이의 정확한 기능 관계 및 세부 수준 면에서 다릅니다.이 범주의 일부 모델은 출력 스파이크의 발생 순간만 예측하고("활동 잠재력"이라고도 함) 다른 모델은 더 상세하고 세포 하위 프로세스를 설명합니다.이 범주의 모델은 결정론적 또는 확률론적 모델일 수 있다.
2. 자연 자극 또는 약리학적 입력 뉴런 모델 – 이 범주의 모델은 약리학적 또는 자연적일 수 있는 입력 자극과 스파이크 사건의 확률 사이를 연결합니다.이러한 모델의 입력 단계는 전기적인 것이 아니라 오히려 약리학적(화학적) 농도 단위 또는 빛, 소리 또는 기타 형태의 물리적 압력과 같은 외부 자극을 특징짓는 물리적 단위를 가진다.또한 출력단은 전기전압이 아닌 스파이크 이벤트의 확률을 나타낸다.

비록 과학과 공학에서 다른 추상화/상세 수준에 대한 여러 가지 서술적 모델을 갖는 것은 드문 일이 아니지만, 서로 다른, 때로는 모순되는 생물학적 뉴런 모델의 수는 예외적으로 많다.이러한 상황은 부분적으로 많은 다른 실험 환경, 그리고 측정 효과와 많은 세포의 상호작용으로부터 단일 뉴런의 본질적 특성을 분리하는 어려움의 결과이다(네트워크 효과).통합 이론으로의 수렴을 가속화하기 위해 각 범주에서 여러 모델을 나열하고 해당되는 경우 보조 실험에 대한 참조도 나열합니다.

뉴런 모델의 목적

궁극적으로, 생물학적 뉴런 모델은 신경계의 작동의 기초가 되는 메커니즘을 설명하는 것을 목표로 한다.그러나 몇 가지 접근방식은 보다 현실적인 모델(예: 기계학적 모델)에서 보다 실용적인 모델(예: 현상학적 모델)^[2]로 구분할 수 있다.모델링은 실험 데이터를 분석하고 다음과 같은 질문에 대처하는 데 도움이 됩니다: 뉴런의 스파이크는 감각 자극이나 팔 움직임과 같은 운동 활동과 어떻게 관련이 있습니까?신경계가 사용하는 신경 코드는 무엇입니까?모델은 또한 신경 동토장치를 통해 잃어버린 뇌 기능을 회복시키는 맥락에서 중요하다.

전기 입출력 막 전압 모델

이 범주의 모델은 입력 단계의 신경막 전류와 출력 단계의 막 전압 사이의 관계를 설명합니다.이 범주는 Hodgkin의 연구에서 영감을 얻은 (일반화된) 통합 및 화재 모델과 생물물리 모델을 포함한다.1950년대 초 Huxley는 세포막을 뚫고 특정 막 전압/전류를 ^[3][4][5][6]강제할 수 있는 실험 장치를 사용했다.

대부분의 최신 전기 신경 계면은 세포사망과 조직손상을 초래할 수 있는 막파쇄를 피하기 위해 세포외 전기자극을 적용한다.따라서 전기적 뉴런 모델이 세포 외 자극을 어느 정도까지 유지하는지는 명확하지 않다(예:^[7] 참조).

호지킨헉슬리

모형을 뒷받침하는 실험 증거

H&H 모델의 특성	레퍼런스
개별 스파이크 모양	[3][4][5][6]
관련된 이온의 정체성	[3][4][5][6]
축삭간 스파이크 속도	[3]

호지킨-Huxley 모델(H&H 모델)^[3][4][5][6]은 신경세포막을 가로지르는 이온전류의 흐름과 세포의 ^[3][4][5][6]막전압 사이의 관계 모델이다.그것은 오징어 거대 축삭의 세포막을 투과하는 이온 채널의 거동을 설명하는 일련의 비선형 미분 방정식으로 구성됩니다.호지킨과 헉슬리는 이 연구로 1963년 노벨 생리의학상을 받았다.

용량_m C의 셀막을 충전하는 복수의 전압 의존 전류와 함께 전압-전류 관계에 주목한다.

${\displaystyle C_{\mathrm {m}}{\frac {dV(t)}{dt}}=-\sum _{i}I_{i}(t,V)}$

위의 방정식은 총 전하의 변화를 전류에 대한 합으로 설명해야 하는 정전용량의 법칙인 Q = CV의 시간 미분입니다.각 전류는 다음에 의해 주어집니다.

$({displaystyle I(t,V)=g(t,V)\cdot(V-V_{\mathrm {eq}})})$

여기서 g(t,V)는 최대 전도도 θ와 활성화 및 비활성화 분율 m, h의 관점에서 확장될 수 있는 전도도 또는 역저항으로, 사용 가능한 막 채널을 통해 얼마나 많은 이온이 흐를 수 있는지를 결정한다.이 확장은 다음과 같습니다.

${\displaystyle g(t,V)=cdot m(t,V)^{p}\cdot h(t,V)^{q}$

그리고 우리의 분수는 1차 운동학을 따른다.

${\displaystyle {dm(t,V)}{dt}=param frac {m_{\infty}(V)-m(V)}{\tau _{\mathrm {m}}(V)}=\alpha _{\mathrm {m}(V)\cdot (1-m) {m}{m}_m}{m}{m}$

h에 대한 유사한 역학을 사용하여 게이트 분율을 정의하기 위해 θ와_∞ m 또는 α와 β를 사용할 수 있다.

호지킨-Huxley 모델은 추가 이온 전류를 포함하도록 확장할 수 있습니다.일반적으로 여기에는 내부²⁺ Ca 및⁺ Na 입력 전류뿐만 아니라 "누출" 전류를 포함한 다양한⁺ K 외부 전류가 포함됩니다.

최종 결과는 정확한 모형을 위해 추정하거나 측정해야 하는 작은 끝 20개의 모수에 있을 수 있습니다.복잡한 뉴런 시스템의 모델에서 방정식의 수치적 통합은 계산적으로 비용이 많이 든다.Hodgkin의 신중한 단순화-따라서 Huxley 모델이 필요합니다.

게이트 ^[8]변수 간에 설정할 수 있는 동적 관계 덕분에 모델은 2차원으로 축소될 수 있습니다.(원래 ^[9][10]모델에서 고정된 것으로 간주됨) 농도의 진화를 고려하도록 확장할 수도 있다.

완벽한 통합 및 작동

뉴런의 초기 모델 중 하나는 1907년 루이 라피케에 ^[11]의해 처음 연구된 완벽한 적분-발화 모델이다.뉴런은 자극 중에 시간적으로 진화하는 막전압 V에 의해 다음과 같이 입력 전류 I(t)에 의해 표현된다.

${\displaystyle I(t)=C{\frac {dV(t)}{dt}}$

이는 정전용량의 법칙인 Q = CV의 시간 도함수입니다.입력 전류가 인가되면 멤브레인 전압이 일정한 임계값_th V에 도달할 때까지 시간이 지남에 따라 상승합니다. 이때 델타 함수 스파이크가 발생하고 전압이 정지 전위로 재설정된 후 모델이 계속 실행됩니다.따라서 모델의 기동 주파수는 입력 전류가 증가함에 따라 경계 없이 선형적으로 증가합니다.

그 기간 동안 뉴런의 발화를 방지함으로써 뉴런의 발화 빈도를 제한하는 내화 주기_ref t를 도입함으로써 모델을 보다 정확하게 만들 수 있다.상시 입력 I(t)=I 역치전압은 0부터 개시한 후 적분시간_int t_thr=CJ/I 후에 도달한다.리셋 후 내화주기는 데드타임을 도입하여 다음 번 발화까지의 총시간이 t+t가_int 된다_ref.기동 빈도는 총 스파이크 간 간격(데드 타임 포함)의 역수입니다.따라서 일정한 입력 전류의 함수로서의 발화 주파수는

${\displaystyle \!f(I)=subscfrac {I}{C_{\mathrm {}}V_{\mathrm {th}}+t_{\mathrm {ref} }I}}}}.}$

이 모델의 단점은 적응도 누출도 설명하지 않는다는 것입니다.모델이 임계값 미만의 짧은 전류 펄스를 수신하면 나중에 다른 입력이 작동될 때까지 해당 전압 부스트를 영원히 유지합니다.이 특성은 관찰된 신경의 행동과 분명히 일치하지 않는다.다음과 같은 확장은 생물학적 관점에서 통합 및 화재 모델을 더욱 그럴듯하게 만든다.

누출성 통합 및 화재

루이 라피크에서 ^[11]추적할 수 있는 누출성 적분 및 화재 모델은 비누출성 적분 및 화재 모델과 비교하여 막 전위 방정식의 "누출" 항을 포함하고 있으며, 막을 통한 이온의 확산을 반영합니다.모형 방정식은 다음과^[1] 같습니다.

${\displaystyle C_{\mathrm {m} } {\frac {dV_{\mathrm {m}(t)} = I(t)-{\frac {V_{\mathrm {m}}}(t)} {R_{\mathrm {m}}}}}}}}}$

여기서_m V는 세포막을 가로지르는 전압이고_m R은 막 저항이다.(비누출 적분화 모델은 막이 완전 절연체일 경우 무한대 한계_m R에서 검색된다.)모델 방정식은 임계값_th V에 도달할 때까지 임의의 시간 의존 입력에 유효하며, 그 후 막 전위가 재설정됩니다.

일정한 입력의 경우 임계값에 도달하기 위한 최소 입력은 I = V_th / R입니다_thm. 0으로 재설정한다고 가정하면, 작동 주파수는 다음과 같습니다.

${\displaystyle f(I)=begin{case}0,&I\leq I_{\mathrm {th}\left[t_{\mathrm {ref}}-R_{\mathrm {m}}}C_{\log \left(1-{\tfrac {t}}{math})IR_{\mathrm {m} }}\right)\right]^{-1},&I>I_{\mathrm {th}}\end{case}}$

큰 입력 전류를 위해 내화 ^[12]주기가 있는 이전 누출 없는 모델로 수렴합니다.이 모델은 억제성 ^[13][14]뉴런에도 사용될 수 있다.

리키 통합 및 발화 뉴런의 가장 큰 단점은 뉴런 적응을 포함하지 않기 때문에 일정한 ^[15]입력 전류에 반응하여 실험적으로 측정된 스파이크 트레인을 설명할 수 없다는 것이다.이러한 단점은 하나 또는 여러 적응 변수를 포함하고 현재 주입 중인 피질 뉴런의 스파이크 시간을 높은 ^[16][17][18]정확도로 예측할 수 있는 일반 적분 및 화재 모델에서 제거된다.

적응형 통합 및 화재

모형을 뒷받침하는 실험 증거

적응형 통합 및 화재 모델 모델	레퍼런스
시간 의존 입력 전류에 대한 하위 임계값 전압	[17][18]
시간 의존 입력 전류의 기동 시간	[17][18]
스텝 전류 입력에 대한 응답의 점화 패턴	[19][20][21]

신경 적응은 소마에 일정한 전류를 주입하는 경우에도 출력 스파이크 사이의 간격이 증가한다는 사실을 의미한다.적응적 통합-발화 뉴런 모델은 전압 V의 누출적 통합을 하나 또는 여러 적응 변수_k w와 결합한다(교과서 신경^[22] 역학 6.1장 참조).

$\displaystyle _{\mathrm {m} } {\frac {dV_{\mathrm {m}(t)} = RI(t)-[V_{\mathrm {m} } }(t)-E_{\mathrm {m} } ]-R\sum _{k} {k} {k} {k}}$

$\displaystyle _{k}{\frac {dw_{k}(t)}{dt}=-a_{k}[V_{\mathrm {m}}(t)-E_{k}+b_{k}\mathrm {m}}_{f}_{f}{t})$

여기서 ${\displaystyle {\theta }_{}}$ m$${\$displaystyle \tau$ _${m}$은_k 멤브레인 시간 상수, w는 적응 전류 수, ${\displaystyle k_{}}${$displaystyle \tau$ _${k}$는 적응 전류의_k 시간 상수, E는_m 뉴런의 정지 전위, t는^f 디락 델타 함수를 나타낸다.전압이 점화 임계값에 도달할 때마다 전압이 점화 임계값보다 낮은 값 V로_r 재설정됩니다.재설정 값은 모형의 중요한 매개변수 중 하나입니다.가장 단순한 적응 모델은 단일 적응 변수 w만 가지며 k에 대한 합계는 제거됩니다.^[23]

하나 또는 여러 적응 변수를 가진 통합 및 발화 뉴런은 적응, 폭발 및 초기 ^[19][20][21]폭발을 포함한 지속적인 자극에 대한 다양한 신경 발화 패턴을 설명할 수 있다.또한, 여러 적응 변수를 가진 적응형 통합 및 발화 뉴런은 소마에 ^[17][18]시간 의존적인 전류 주입 하에서 피질 뉴런의 스파이크 시간을 예측할 수 있다.

부분 오더 누출 통합 및 화재

계산과 이론의 미적분학의 최근 발전은 분수차 누수 ^[24][25]적분화라고 불리는 새로운 형태의 모델을 이끌었다.이 모델의 장점은 단일 변수로 적응 효과를 포착할 수 있다는 것입니다.모델의 형태는 다음과^[25] 같습니다.

${\displaystyle I(t)-{\frac {V_{\mathrm {m} }(t)} {R_{\mathrm {m} } = C_{\mathrm {m} } {\frac {d^{\alpha} } V_{\mathrm {m {m}(t} } } } } } } } }$

전압이 임계값에 도달하면 재설정됩니다.부분 통합은 실험 데이터에서 ^[24]신경 적응을 설명하기 위해 사용되어 왔다.

'지수적 통합-발화' 및 '적응적 지수적 통합-발화'

모형을 뒷받침하는 실험 증거

적응형 지수 통합 및 실행	레퍼런스
하위 임계값 전류-전압 관계	[26]
스텝 전류 입력에 따른 발화 패턴	[21]
내구성 및 적응성	[27]

지수 적분-발화 ^[28]모델에서 스파이크 생성은 다음 방정식에 따라 지수적입니다.

${\displaystyle {\frac {dV}-{\frac {R}{\tau _{m}}I(t)=param frac {1}{m}}\left[E_{m}-V+\Delta _{T}\exp \frac {V-V}{\frac {V}}}T}} {\Delta _{T}}\right}\right]}$

$여기$서 V$({$$displaystyle$ V$}$는 멤브레인 ${\displaystyle {전위}_{}}$, V$({$T})는$$ 멤브레인 전위 임계값, $({$$\tau_$${$$m$})은$$ 멤브레인 시간 상수, $δT(\$displaystyle ${$m})는$$ 휴지 전위, δTyle\$displaystyle$ \$Delta_{T}$는 샤프니스입니다.활동 전위 개시, 보통 피질 피라미드 ^[26]뉴런의 경우 약 1mV.막 전위는 V $({$와 $교차$하면 유한 시간 ^[29]내에 무한대로 분산됩니다.수치 시뮬레이션에서 막 전위가 임의의 임계값($V$ T$(\$T$\})$보다 훨씬 큰 경우)에 도달하면 적분이 정지됩니다. 이때 막 전위가 V 값으로_r 재설정됩니다. 전압 재설정 값 V는_r 모델의 중요한 파라미터 중 하나입니다.중요한 것은 위의 방정식의 오른쪽에는 실험 ^[26]데이터에서 직접 추출할 수 있는 비선형성이 포함되어 있다는 것입니다.이런 의미에서 지수적 비선형성은 실험 증거에 의해 강하게 뒷받침된다.

적응 지수 적분 및 발화 뉴런에서 전압 방정식의 위의 지수 비선형성은 적응 변수 w와 결합됩니다.

$\displaystyle _{m}{\frac {dV}{dt}}=RI(t)+\왼쪽[E_{m}-V+\Delta _{T}\exp \left({\frac {V-V_{)T}}{\Delta _{T}}\right)\right]-Rw}$

${\displaystyle\frac {dw(t)}{dt}=-a[V_{\mathrm {m}(t)-E_{\mathrm {m}}]-w+b\displays \f}(t-t^{f})$

어디 wτ{\displaystyle \tau}. 적응 시간 규모로 현재 중요한 모델 매개 변수를 나타내고 있는 전압 로그인 설정 값 Vr, 내재적 한계 VT{\displaystyle V_{T}}, 시간 정수τ{\displaystyle \tau}과τ m{\displaystyle \tau_{m}}뿐만 아니라 연결 장치 매개 변수와 b.적응형 지수 적분 및 화재 모델은 지수 적분 및 화재 모델의 실험적으로 도출된 전압 비선형성을 계승한다.하지만 이 모델을 넘어서, 이것은 또한 적응, 폭발, ^[21]초기 폭발 등 지속적인 자극에 반응하는 다양한 신경 발화 패턴을 설명할 수 있습니다.그러나 적응이 전류 형태이기 때문에 이상 과분극이 나타날 수 있다.이 문제는 ^[30]컨덕턴스로 표현함으로써 해결되었다.

막전압 및 스파이크 타이밍의 확률적 모델

이 범주의 모델은 특정 수준의 확률성을 포함하는 일반화된 통합 및 화재 모델이다.실험의 피질 뉴런은 동일한 자극이 ^[31][32]반복될 경우 한 번의 시행과 다음 번의 시행 사이에 약간의 변화가 있더라도 시간에 의존하는 입력에 신뢰성 있게 반응하는 것으로 밝혀졌다.뉴런의 확률성은 두 가지 중요한 원천을 가지고 있다.첫째, 입력 전류가 소마에 직접 주입되는 매우 제어된 실험에서도 이온 채널은 확률적으로^[33] 개폐되며, 이 채널 노이즈는 막 전위의 정확한 값과 출력 스파이크의 정확한 타이밍에 작은 양의 변동으로 이어진다.둘째, 피질 네트워크에 내장된 뉴런의 경우,^[22] 대부분의 입력은 뇌의 다른 어딘가에서 관찰되지 않은 뉴런에서 나오기 때문에 정확한 입력을 통제하기가 어렵다.

확률성은 근본적으로 다른 두 가지 형태로 스파이크 뉴런 모델에 도입되었다: (i) 노이즈의 입력 전류가 뉴런 ^[34]모델의 미분 방정식에 추가되거나 (ii) 스파이크 생성 과정이 노이즈가 발생한다.^[35]두 경우 모두, 수학 이론은 연속 시간 동안 개발될 수 있으며, 그 후 컴퓨터 시뮬레이션에서의 사용을 원할 경우 이산 시간 모델로 변환됩니다.

뉴런 모델에서 스파이크 열차와 신경 코드의 가변성에 대한 소음의 관계는 신경 코딩과 교과서 신경 ^[22]역학 7장에서 논의된다.

노이즈 입력 모델(확산 노이즈)

네트워크에 내장된 뉴런은 다른 뉴런으로부터 스파이크 입력을 받는다.스파이크 도착 시간은 실험가에 의해 제어되지 않기 때문에 확률적인 것으로 간주할 수 있다.따라서 비선형성 f(v)를 갖는 (잠재적으로 비선형) 통합-발화 모델은 두 가지 입력을 받습니다. 실험자가 제어하는$$ $입력$I (${\displaystyle t}$) \ $displaystyle$I ($$${\displaystyle t}$ )${\displaystyle {}^{}{\mathrm{a}}^{}}$ $a{\displaystyle {}^{}}$ a thus ${\displaystyle {thus\mathrm{}}^{}}$ 、 t${\displaystyle }$（ t $）$ \ $display style$ I^ { \$rm$ { $noise$} （ $t$） 。

$\displaystyle _{m}{\frac {dV}{dt}}=f(V)+RI(t)+RI^{\text{noise}}(t)}$

Stein의 모델은^[34] 누출성 통합 및 발화 뉴런과 평균 0 및 단위 분산을 갖는 정상 백색 노이즈 $전류{\displaystyle {}^{}}$ I ${\displaystyle {\mathrm{n}}^{}}$ ${\displaystyle \mathrm{oi}}$ ${\displaystyle {\mathrm{s}}^{}e}$ (${\displaystyle }$t ) ${\displaystyle =}$ ${\displaystyle (}$ (${\displaystyle t}$) { $display$ I^ { \$rm${$noise$} ( t ) =$\xi$ ($$t )의$$ 특수한 경우이다.서브임계정에서 이러한 가정은 Ornstein의 방정식을 산출한다.움렌벡법

$\displaystyle _{m}{\frac {dV}{dt}}=[E_{m}-V]+RI(t)+R\xi(t)}$

단, 표준 Ornstein과는 대조적으로-Uhlenbeck 프로세스, V가 점화 임계값_th ^[34]V에 도달할 때마다 멤브레인 전압이 재설정됩니다. Ornstein의 간격 분포를 계산합니다.임계값이 있는 일정한 입력을 위한 Uhlenbeck 모델은 첫 번째 통과 시간 문제를 ^[34][36]야기합니다.스타인의 뉴런 모델과 그 변형은 일정한 입력 ^[36]전류 하에서 실제 뉴런에서 스파이크 트레인의 스파이크 간격 분포를 맞추기 위해 사용되어 왔다.

수학 문헌에서, 오르슈타인의 위의 방정식은-Uhlenbeck 프로세스는 다음 형식으로 작성됩니다.

$\displaystyle dV=[E_{m}-V+RI(t)]{\frac {dt}{\flac _{m}}+\flac \,dW}$

$여기$서 ${\$ { $displaystyle \sigma }$는 노이즈 입력의 진폭이고 dW는 Wiener 프로세스의 증분입니다.시간 스텝 dt를 사용한 이산 시간 구현의 경우 전압 업데이트는^[22] 다음과 같습니다.

$\displaystyle \Delta V=[E_{m}-V+RI(t)]{\frac {Delta t}{\flac _{m}}+\flacrt {m}}y}$

여기서 y는 평균 단위 분산이 0인 가우스 분포에서 도출됩니다.전압은 점화_th 임계값 V에 도달하면 재설정됩니다.

노이즈 입력 모델은 일반화된 통합 및 화재 모델에서도 사용할 수 있습니다.예를 들어, 노이즈가 많은 입력 읽기를 사용하는 지수 통합 및 실행 모델

$\displaystyle \m}{\frac {dV}{dt}}=E_{m}-V+\Delta _{T}\exp \leftfac {V-V_{T}}{\Delta _{T}}\right)+RI(t)+R\xi(t)}$

일정한 결정론적 $입력$의 경우${\displaystyle }$I (${\displaystyle t}$ ) $=$ ${\displaystyle {I\mathrm{}}_{}}$ 0 {\$displaystyle I$(t)=$I_{0}:$ 평균$$ 발화율은 ${\displaystyle {I\mathrm{}}_{}}$ 0$({$^[37]의 함수로 계산할 수 있다.이것은 실험가들이 뉴런의 특성을 나타내기 위해 주파수-전류 관계(f-I-곡선)를 자주 사용하기 때문에 중요하다.에서의 전송 기능이기도 합니다.

노이즈가 많은 입력과 함께 누출되는 통합과 발화는 스파이크 ^[38]뉴런의 네트워크 분석에 널리 사용되어 왔다.노이즈 입력은 노이즈가 없는 궤적을 중심으로 역치 이하의 막 전위의 확산으로 이어지기 때문에 '확산 노이즈'라고도 불린다(Johannesma,^[39] 노이즈가 있는 스파이킹 뉴런의 이론은 교과서 신경역학 8.^[22]2장에서 검토된다).

노이즈가 많은 출력 모델(에스케이프 노이즈)

결정론적 Integrate-and-fire 모델에서는 막 전위 V(t)가 $임계값{\displaystyle {}_{}}$ ${\displaystyle V_{}}$ t$$ {displaystyle $V_{th$에 도달하면 스파이크가 생성됩니다.노이즈 출력 모델에서는 엄격한 임계값은 다음과 같이 노이즈 임계값으로 대체됩니다.시간 t의 각 시점에서 순간 확률 강도 또는 '회피율'로 확률적으로 스파이크를 생성한다.

$(\displaystyle \rho (t)=f(V(t)-V_{th})}$

이는 멤브레인 전압 V(t)와 ${\displaystyle {임계값}_{}}$ V t$$ {\$displaystyle V_{th$^[35] 사이의 순간적인 차이에 따라 달라집니다. '탈출 속도'$$f${\displaystyle }$ {\$displaystyle$f}($$생물학적^[17] 데이터와 일치함)에 대한 일반적인 선택은

${\displaystyle f(V-V_{th})=flac {1}{\display_{0}}\exp[\display(V-V_{th})}$

여기서 ${\displaystyle {\theta \mathrm{}}_{}}$0(\$displaystyle \display_{0})$은 멤브레인 전위가 임계값에 도달했을 때 스파이크가 얼마나 빨리 발사되는지를 나타내는 시간 $상수$이고$$β(\$displaystyle\display$}는$$샤프니스 파라미터입니다.β ${\displaystyle \to }$β {\$displaystyle \to \infty}$의 경우 역치가 날카로워지고 막 전위가 아래에서 역치에 도달하는 순간 스파이크 소성이 결정적으로 발생한다.실험에서^[17] 발견된 샤프니스 값은${\displaystyle }$1/${\displaystyle \beta m}$ $({displaystyle$1/\$beta\약$ 4mV$)$이며, 이는 막 전위가 공식 소성 임계값보다 몇 mV 낮아지면 신경 소성이 불가능함을 의미한다.

부드러운 임계값을 통한 탈출 속도 프로세스는 교과서 신경 ^[22]역학 9장에서 검토한다.

이산 시간 모델의 경우 스파이크가 확률로 생성됩니다.

$\displaystyle P_{F}(t_{n})=F[V(t_{n})-V_{th}}$

$시간{\displaystyle {}_{}}$ $(\$과 임계값 ${\displaystyle V_{}}$ ${\displaystyle t_{}}$h(\$displaystyle V_{th$}) 사이의 순간적인 차이에 따라 달라집니다$.$^[44]함수 F는 종종 인공 신경망의 업데이트 다이내믹스와 마찬가지로 경사 파라미터$\theta {\displaystyle }$ {$displaystyle \tanh$ $\}$^[35]를 갖는 표준 $S자형{\displaystyle }$F$(x$ $= 0$.5$[1+\tanh(\gamma$ x$)]$로 간주됩니다.그러나 F의 함수 형태는 위에서${\displaystyle }$F ( y${\displaystyle {}_{}}$n )${\displaystyle 11}$ - exp ${\displaystyle [}$ [ y ${\displaystyle {}_{}\mathrm{}}$ ${\displaystyle t}$] \ $displaystyle$F ( $y$_ { $n$} \$1$1 - \$exp$[ y _ { n } \ $delta ]$ 로 $소개$한 $확률적$ 강도 f { displaystyle$f$} 에서$$$$ ${\displaystyle {도출}_{}}$할 ${\displaystyle 수}$도 있다${\displaystyle {}_{}}$ ${\displaystyle {여기}_{}}$서 ${\displaystyle y_{}}$n ${\displaystyle {}_{}}$V - t )문턱값에 ^[35]대응합니다.

출력 노이즈가 있는 통합 및 화재 모델을 사용하여 임의의 시간 의존 ^[17]입력에서 실제 뉴런의 PSTH를 예측할 수 있습니다.비적응 적분 및 발화 뉴런의 경우, 일정한 자극 아래에서의 간격 분포는 정상 갱신 이론에서 계산할 수 있다.^[22]

Spike 응답 모델(SRM)

모형을 뒷받침하는 실험 증거

스파이크 반응 모형	레퍼런스
시간 의존 입력 전류에 대한 하위 임계값 전압	[18][17]
시간 의존 입력 전류의 기동 시간	[18][17]
스텝 전류 입력에 대한 응답의 점화 패턴	[45][46]
스파이크 간 간격 분포	[45][35]
스파이크 애프터 퍼텐셜	[18]
내화성 및 동적 발화 임계값	[18][17]

주요 기사: Spik 응답 모델

스파이크 응답 모델(SRM)은 스파이크 ^[35][47][45]생성을 위한 비선형 출력 노이즈 프로세스와 결합된 하위 임계값 막 전압의 일반적인 선형 모델입니다.시간 t에서의 막전압 V(t)는

$\displaystyle V(t)=\sum _{f}\eta (t-t^{f})+\int _{0}^{\infty}\kappa (s)I(t-s),ds+V_{\mathrm {rm {rm {rm}}}}}$

여기서^f t는 뉴런 스파이크 수 f의 기동시간, V는_rest 입력이 없는 경우의 휴지전압, I(t-s)는 시간 t-s의 입력전류,${\displaystyle }\delta {\displaystyle }$($)$ {$displaystyle \kappa(s)}$는 t-s의 전압에 대한 입력전류 펄스의 기여도를 나타내는 선형필터(커널이라고도 함)입니다.시간 ${\displaystyle t^{}}$ ${\$ t$^{f}}$에서 스파이크에 의한 전압의 기여는 내화 커널${\displaystyle \delta }$ ( t${\displaystyle }$- ${\displaystyle {}^{}{f}^{}}$ )$${ $displaystyle \eta$( t - $t^{f$에서 기술하고 있으며, 특히 $\delta {\displaystyle }$ ${\displaystyle (t}$ - ${\displaystyle t^{}}$f$$) { $displaystyle \eta$( t - t$^{f}$은 스파이크 후의 리셋과 스파이크 후의 시간을 기술하고 있다.모두 스파이크를 따라갑니다.따라서 이는 내화성과 ^[35][18]적응의 결과를 나타냅니다.전압 V(t)는 누출 적분 및 화재 모델의 미분 방정식이 임의의 수의 스파이크 트리거 적응 ^[19]변수에 결합된 결과로 해석될 수 있습니다.

스파이크 발화는 확률적이며 시간 의존적인 확률 강도(순간 속도)로 발생한다.

$\displaystyle f(V-\vartheta(t))=param frac {1}{\param _{0}}\exp[\param (V-\vartheta (t)]}$

${\displaystyle {파라미터}_{}}$가 0$({$ $및$ β({$displaystyle\$displaystyle$\display})$이고 동적 임계값$t)$은 다음과 같습니다.

$\displaystyle \vartheta (t)=\vartheta _{0}+\sum _{f}\theta _{1}(t-t^{f})$

비활성 뉴런의 여기ϑ 0{\displaystyle \vartheta_{0}}은 쏘고 한계점 시험 θ 1(t−지 f){\displaystyle \theta_{1}(t-t^{f})}당시 고정 임계 값의 경우 스파이크 tf{\displaystyle t^{f}}.[17][18] 후 문지방의 증가에 대해 설명합니다,{θ 1(t−지 f)을 가져오거나 설정합니다.\display$style \theta$ _${1}(t-t^{f})}$ $=$ 0.β $β$의 $경우{\displaystyle }$(\$displaystyle$\to$\infty)$ 임계값$$ 프로세스는 ^[22]결정론적입니다.

스파이크 응답 모델을 특징짓는 $필터{\displaystyle }$ ${\displaystyle ,,\mathrm{11}}$,$$, \$displaystyle \eta,$ \$kappa,$ \$theta$ _${1$}의$$ 시간 경로는 실험 데이터에서 ^[18]직접 추출할 수 있습니다.최적화된 매개 변수를 사용하여 SRM은 2mV의 정밀도로 시간 의존 입력에 대한 하위 임계값 멤브레인 전압의 시간 경로를 설명하고 4ms의 ^[17][18]정밀도로 대부분의 출력 스파이크의 타이밍을 예측할 수 있습니다.SRM은 선형-비선형-포아송 캐스케이드 모델(일반화 선형 ^[43]모델이라고도 함)과 밀접하게 관련되어 있습니다.일반화 선형^[48] 모델을 위해 개발된 방법을 사용한 SRM과 같은 확률적 뉴런 모델의 매개변수의 추정은 교과서 신경 ^[22]역학 10장에서 논의된다.

스파이크 반응 모델이라는 이름은 네트워크에서 뉴런 i에 대한 입력 전류가 다른 뉴런의 스파이크에 의해 생성되기 때문에 네트워크의 경우 전압 방정식이 다음과 같이 됩니다.

$({displaystyle V_{i}(t)=\sum _{f}\eta _{i}(t-t_{i}^{f})+\sum _{n}w_{ij'}\varepsilon _{ij}(t-t_{j}^{f'}+)V_{\mathrm {rest}}}$

$여기$서 t ${\displaystyle j_{}^{}}$ ${\displaystyle {{}^{}}_{}^{}}$ ${\$ {\$displaystyle t_{$j}^{$f'}$는 뉴런 j(${\displaystyle 즉}$, 스파이크열)의 발화 ${\displaystyle {시간}_{}}$이고${\displaystyle {}_{}{}_{}^{}}$ -$$i ${\displaystyle {}_{}^{}}$)(\$displaystyle$ \${\displaystyle {eta}_{}}$$$_${i$}($t-t_{$$i}^{$$f{\displaystyle {}_{}}$})는 뉴런의 스파이크와 스파이크 후의 $시간$ 경로를 $.$${\displaystyle {{}^{}}_{}^{}}$f ${\displaystyle {)}_{}^{}}$ $)({displaystyle \varepsilon$ _${ij}(t-t_{j}^{f'})$는 시냅스 전 뉴런의 $스파이크{\displaystyle {}_{}^{}}$ ${\displaystyle {{}^{}}_{}^{}}$ f$$†({$displaystyle t_{j}^f'})$에 의해 발생하는 흥분성 또는 억제성 시냅스 후 전위(PSP)의 진폭과 시간 경로를 나타낸다.PSP의 타임코스$$ ${\displaystyle i_{}j}$ (${\displaystyle }$s $){$ $displaystyle$ \ $varepsilon _$ { $ij$$\}$^[22]$$(${\displaystyle }$s$)$는 막필터를 가진${\displaystyle }뉴런{\displaystyle }$ $j$에서 시냅스 전 스파이크가 도달하여 $발생$하는 시냅스 후 $전류{\displaystyle }$I ( $t$)의 분해에 기인한다$.$

SRM0

그 SRM0[45][49][50]은 확률적인 뉴런 모델time-dependent 비선형 갱신설과 스파이크 Renose 모델(SRM)의 간소한 관련이 있다. 그 SRM은 위에서 도입의 전압 방정식에 가장 큰 차이점{\displaystyle \eta(s)}이 없가중 징후는 용어의 내화 커널 η(s)다. 지난 sp에ikes: 가장 최근의 스파이크($시간{\displaystyle \stackrel{}{}}$t$^\displaystyle\hat$ {t$\})$만 문제가 됩니다.또 다른 차이점은 임계값이 일정하다는 것입니다.SRM0 모델은 이산 시간 또는 연속 시간 내에 공식화할 수 있습니다.예를 들어, 연속 시간에서 단일 뉴론 방정식은 다음과 같습니다.

${\displaystyle V(t)=\eta(t-{\hat {t})+\int _{0}^{\infty}\kappa(s)I(t-s),ds+V_{\mathrm {rm {rm}}}}$

SRM0의^[45] 네트워크 방정식은 다음과 같습니다.

$({displaystyle V_{i})(t\mid {hat {t}}_{i})=\eta _{i}(t-{\hat {t}_{i})+\sum _{j}w_{ij}\sum _{f}\varepsilon _{ij}(t-{\hat {t}}_{i},t-t^{f})+V_{\mathrm {rest}}}$

$여기$서 t${\displaystyle {\stackrel{}{}}_{}}$^$$ (\$displaystyle {t}}_{$i$$})는 마지막 발화 시간 뉴런 i입니다.시냅스 후 전위 ${\displaystyle {\mathrm{\delta i}}_{}}$j \ $displaystyle$\$varepsilon$_ { $ij}$의 시간 경로는 또한 굴절 ^[49]시 막 전도율의 변화를 설명하기 위해 뉴런 i의 마지막 스파이크 이후의 시간에 의존할 수 있음에 유의한다.순간 발화율(폭발 강도)은

${\displaystyle f(V-\vartheta)=flac {1}{\display_{0}}\exp[\display(V-V_{th})]$

${\displaystyle {여기}_{}}$서 V t$$(\$displaystyle V_{th})$는 고정 점화 임계값입니다.따라서 뉴런 i의 스파이크 발사는 입력과 뉴런 i가 마지막 스파이크를 발사한 이후의 시간에만 의존합니다.

그 SRM0으로 꾸준하게 투입에 대한interspike-interval 유통 중간값은 내화 커널 η{\displaystyle \eta}의 모양에 .[35][45]게다가는 고정형frequency-current 관계는 탈출률에서 내화 커널 η{\displaystyle \eta}.[35]용과 조합에서 계산할 수 있는 연결될 수 있다.45을 생성하는 appr으로커널의 오프리에이트 선택, SRM0은 Hodgkin-Huxley 모델의 역학을 높은 ^[49]정확도로 근사한다.또한 임의의 시간 의존 입력에 대한 PSTH 응답을 ^[45]예측할 수 있다.

갈베스-뢰체르바흐 모형

갤브스-뢰처바흐^[51] 모델은 스파이크 반응 모델 SRM0 및 누출 적분-발화 모델과 밀접하게 관련된 확률적 뉴런 모델이다.이는 본질적으로 확률적이며, 시간에 의존하는 비선형 갱신 이론과 연결된 SRM0과 같다.모델 사양에 따라 특정 $i가$$$일정 $기간$ 동안 급증할 확률은 $다음$과 같이 기술할 수 $있습니다.$

${\displaystyle \mathrm {Prob}(i)=1\mid {mathcal {F}_{t-1}=\varphi _{i}{Biggl (}\sum _{j\in I}W_{j\rightarrow i}\sum _S=L_{t-1}^{g-1}^{i}^{t}}^{t}^{i}}}}$

${\displaystyle {여기}_{}}$서 W j ${\displaystyle {\to }_{}}$({$displaystyle W_{j\rightarrow$i})는$$$$ 시냅스 가중치로 $뉴런{\displaystyle }$j$(style$ j)가 뉴런$$i(\$displaystyle$ i$)$에 미치는 영향을 $,$ ${\displaystyle g_{}}$(\$displaystyle g_{j})$는 누설을 나타내며$$, ${\displaystyle L_{}^{}}$ $(\$는 $뉴런$의 스파이킹 이력을 나타냅니다$.$$tyle$$$i를$$ t$\displaystyle$t보다 $먼저{\displaystyle }$ 표시합니다.

${\displaystyle L_{t}^{i}=\sup\{s:X_{s}(i)=1\}.$

중요한 것은 뉴런 i의 스파이크 확률은 스파이크 입력(커널 ${\displaystyle g_{}}$${\displaystyle {}_{}}$j {\$displaystyle g_{j$}}, $인자{\displaystyle {}_{}}$ $W_{j\to$i$\})$과 최신 출력 스파이크 타이밍(t ${\displaystyle -}$ ${\displaystyle {}_{}^{}}$ {\$displaystyle t-L_{t^{i}})$에만 의존한다는 점이다.

멤브레인 전압의 교훈적 완구 모델

이 범주의 모델은 멤브레인 전압을 입력의 함수로 정성적으로 설명하는 매우 단순화된 완구 모델입니다.이들은 주로 교육에서 교훈적인 이유로 사용되지만 대규모 시뮬레이션이나 데이터 적합에 유효한 뉴런 모델로 간주되지 않는다.

피츠휴-나구모

Hodgkin에 대한 포괄적인 심플화-Huxley는 FitzHugh와 Nagumo에 의해 1961년과 1962년에 소개되었다.비선형 정피드백막 전압에 의한 "재생 자기 들뜸"과 선형 음피드백 게이트 전압에 의한 회복을 기술하기 위해 그들은 다음과 같이 기술된 모델을 개발했다^[52].

${\displaystyle {dcl}{\dfrac {dV}{dt}}&=V-V^{3}/3-w+I_{\mathrm {ext}}\dfrac {dw}{dt}}&=&V-a-bw\end{array}}$

여기서도 일반 게이트 전압 w가 느린 막 모양 전압과 입력 전류가 있고 a = -0.7, b = 0.8, δ = 1/0.08 매개 변수를 실험적으로 결정합니다.생물학에서 명확하게 파생될 수는 없지만, 이 모델은 단순한 ^[53]단순화가 아니라 단순화되고 즉시 사용 가능한 역학을 허용합니다.실험적인 지지는 약하지만, 이 모델은 위상 평면 분석을 통해 스파이크 발생의 역학을 도입하는 교훈적인 도구로서 유용하다.신경 모델링의^[54] 교과서 방법 7장 참조

모리스-레카

1981년 모리스와 르카는 호지킨을 결합했다.Huxley 및 FitzHugh-Nagumo는 지연 정류 칼륨 채널을 가진 전압 게이트 칼슘 채널 모델로 모델화하며, 다음과 같이 표현됩니다.

${\displaystyle {begin{aligned}&C{\frac {dV}{dt}}&=&-I_{\mathrm {ion}}(V,w)+I\\[6pt]&{\frac {dt}&=\varphi \cdot {w_{\infty }-w}{\flac _{w}}\end {aligned}}}$

${\displaystyle {\mathrm{여기}}_{}}$서 I ${\displaystyle {\mathrm{o}}_{}}$n (${\displaystyle V}$ ,${\displaystyle w}$ ) ${\displaystyle =}$ ${\displaystyle {\stackrel{}{}c}_{\mathrm{}}}$ C ${\displaystyle a_{}{}_{}}$ m ${\displaystyle {\infty \mathrm{}}_{}}$（${\displaystyle V}$ - ${\displaystyle {V\mathrm{}}_{}}$ C${\displaystyle {}_{}{\mathrm{a}}_{}}$ ${\displaystyle ）}$ + ${\displaystyle {\stackrel{}{}}_{}}$ ${\displaystyle {\stackrel{}{¯}}_{}}$ ${\displaystyle K_{\mathrm{}}}$ ${\displaystyle w_{}}$ ${\displaystyle （V}$ - ${\displaystyle {}_{}}$ ${\displaystyle {K\mathrm{}}_{}}$） + ${\displaystyle {\stackrel{}{}}_{}}$ ${\displaystyle {\stackrel{}{¯}}_{}}$ ${\displaystyle L_{\mathrm{}}{（}_{}V}$ - ${\displaystyle {V\mathrm{}}_{}}$ - L$）$ { $displaystyle$I_${\mathrm {ion$}($V,$ w)$$= {$g}$ {gar$}$$}\cdot(V-V_{\mathrm$ {L$}$^[12]})}.모델의 실험적인 지원은 약하지만, 위상 평면 분석을 통해 스파이크 발생의 역학을 도입하는 교훈적인 도구로서 유용하다.신경 ^[54]모델링의 교과서 방법 7장을^[55] 참조하십시오.

Morris-Lecar 모델과 매우 유사한 2차원 뉴런 모델은 Hodgkin-Huxley 모델에서 단계별로 도출할 수 있습니다.Neuroonal Dynamics ^[22]교과서 4.2장을 참조하십시오.

힌드마쉬-로즈

1984년^[56] 힌드마쉬와 로즈는 피츠휴-나구모 모델을 기반으로 3개의 결합된 1차 미분 방정식으로 기술된 신경 활동 모델을 제안했다.

${\displaystyle {aligned}&{\frac {dt}}&=&y+3x^{2}-x^{3}-z+I\\[6pt]&{\frac {dy}{dt}}&=1-5x^{2}-y\[6pt]&{\frac {dz}{dt}}&=&r\cdot(4(x+{\tfrac {8}{5}}-z})\end{aligned}})$

r = x² + y² + z² 및 r ≤ 10을⁻² 사용하여² z 변수가 매우 느리게 변화하도록 합니다.이 추가적인 수학적 복잡성은 막 전위에 대해 카오스 역학을 포함하는 모델의 x 변수로 설명되는 매우 다양한 동적 동작을 허용합니다.이것은 힌드마쉬-로즈 뉴런 모델을 매우 유용하게 만든다. 왜냐하면 여전히 단순하기 때문에, 실험에서 관찰된 활동 전위의 많은 다른 발화 패턴, 특히 폭발에 대한 질적인 설명을 할 수 있기 때문이다.그럼에도 불구하고 장난감 모형으로 남아 있으며 실험 데이터에 적합되지 않았습니다.버스트 ^[56]다이내믹스의 참조 모델로 널리 사용되고 있습니다.

Theta 모형과 2차 적분-발화.

Theta 모델 또는 Ermentrout-Kopell 표준 유형 I 모델은 2차 적분 및 화재 모델과 수학적으로 동등하며, 이는 다시 지수 적분 및 화재 모델과 Hodgkin-Huxley 모델에 대한 근사치이다.이것은 분기점에 가까운 일정한 입력을 위한 일반적인 모델 중 하나이기 때문에 표준 모델이라고 불리며, 이는 무음에서 반복으로의 ^[57][58]전환에 가깝다는 것을 의미합니다.

세타 모델의^[22][57][58] 표준 공식은 다음과 같습니다.

$(\displaystyle {d\theta (t)}{dt}}=(I_{0})[1+\cos(\theta)]+[1-\cos(\theta)]}$

2차 적분-발화 모델의 방정식은 다음과 같다(교과서 신경역학 5.3장 참조).

$\displaystyle \mathrm {m} } {\frac {dV_{\mathrm {m}(t)} {dt} =(I_I_{0}) R+[V_{\mathrm {m}(t)-E_{\mathrm {m} } } [V_{\mathrm {m} }(t)-V_{\mathrm {T} }}$

세타 모델과 2차 적분-발화의 등가성은 스파이킹 뉴런 ^[1]모델의 4.1.2.2장에서 검토된다.

시간이 지남에 따라 변화하거나 분기점에서 멀리 떨어져 있는 입력 I(t)의 경우, 실제 뉴런이 지수 적분-발화 ^[26]모델의 비선형성을 나타내기 때문에 지수 적분-발화 모델을 사용하는 것이 선호된다.

뉴런 모델을 코드하는 감각 입력 자극

이 범주의 모델은 빛, 소리, 촉각 또는 냄새와 같은 자연 자극을 수반하는 실험에 따라 도출되었습니다.이러한 실험에서, 각 자극 제시에서 발생하는 스파이크 패턴은 시험마다 다르지만, 여러 시험의 평균 반응은 종종 명확한 패턴으로 수렴된다.따라서 이 범주의 모델은 입력 자극과 스파이크 발생 사이의 확률적 관계를 생성한다.중요한 것은, 기록된 뉴런은 종종 감각 뉴런 뒤에 여러 처리 단계 뒤에 위치하기 때문에, 이러한 모델들은 처리 단계의 시퀀스의 효과를 콤팩트한 형태로 요약한다.

비균질 포아송 공정 모형(Siebert)

Siebert는^[59][60] 청각 ^[59][60]시스템을 포함한 실험에 따라 비균질 포아송 프로세스 모델을 사용하여 뉴런 스파이크 발화 패턴을 모델링했다.Siebert에 따르면 시간${\displaystyle }$간격 [${\displaystyle t,}$ ${\displaystyle t}$ + ${\displaystyle {\delta }_{}}$t$]({displaystyle [t,t+\Delta$ _${t}))$에서 스파이크 이벤트가 발생할 확률은 음이 아닌 $함수{\displaystyle }$ g${\displaystyle [s}$ ( $]($t$)$ {$displaystyle$ g$[s(t$에 비례한다. $여기$서${\displaystyle }$s$displaystyle$s($tyle$ s($t$$):$

$\displaystyle P_{\text{spike}}(t\in [t',t'+\Delta _{t})=\Delta _{t}\cdot g[s(t)]}$

시버트는 낮은 자극 강도에 대해${\displaystyle }$g [${\displaystyle s}$ (${\displaystyle }$${\displaystyle t}$)${\displaystyle ]}$$$${\displaystyle {}^{}}$ ${\displaystyle s}$2 ( t$$){ $display style$ g$[s($t)]\$propto s^{2}($t$$$)\}$를 $포함$한${\displaystyle }여러{\displaystyle }$ ${\displaystyle \mathrm{기능}}$을${\displaystyle }$g [ s ( ${\displaystyle t}$ ) \ $displaystyle$ g[s$($$$t ) ] { displaystyle s }로서 고려했다.

Siebert 모델의 주요 장점은 단순함이다.모델의 단점은 다음과 같은 현상을 제대로 반영할 수 없다는 것이다.

• 단계 자극에 대한 반응으로 신경 발화 활동의 일시적인 강화.
• 발사율의 포화도.
• 짧은 간격의 스파이크 간격 히스토그램 값(0에 가깝음)입니다.

이러한 단점은 연령 의존적 포인트 프로세스 모델과 2가지 상태 마르코프 모델에 ^[61][62][63]의해 해결된다.

내화성 및 연령 의존성 점 프로세스 모델

베리와 마이스터는^[64] 시간 의존적 자극 s(t)에 의존하는 함수 f(s(t)와 마지막 스파이크 이후 시간에 의존하는 회복${\displaystyle }$함수 ${\displaystyle w(t\stackrel{}{}}$- t$^)\display style$ w$(t-{\hat {t}}})$의 산물로 스파이크를 예측하는 확률적 모델을 사용하여 신경 굴절성을 연구했다.

$(\displaystyle \rho(t)=f(s(t)w(t-{\hat {t}})))$

이 모델을 비균질 마르코프 간격(^[65]IMI) 프로세스라고도 합니다.비슷한 모델들이 청각 ^[66][67][68]신경과학에서 수년간 사용되어 왔다.이 모형은 마지막 스파이크 시간을 기억하기 때문에 Poisson이 아니며 시간에 의존하는 갱신 모형에 ^[22]속합니다.이는 기하급수적인 이스케이프 ^[22]레이트를 가진 SRM0 모델과 밀접하게 관련되어 있습니다.중요한 것은 PSTH 응답뿐만 아니라 스파이크 간격 ^[65][66][68]통계량도 기술할 수 있도록 에이징 의존 포인트 프로세스 모델의 파라미터를 적합시킬 수 있다는 것입니다.

선형-비선형 포아송 캐스케이드 모형 및 GLM

선형-비선형-포아송 캐스케이드 모델은 비선형 스파이크 생성 ^[69]단계가 이어지는 선형 필터링 프로세스의 캐스케이드입니다.출력 스파이크가 선형 필터링 프로세스를 통해 피드백되는 경우, 우리는 신경과학에서 GLM(^[43][48]Generalized Linear Model)로 알려진 모델에 도달합니다.GLM은 수학적으로 이스케이프 노이즈가 있는 스파이크 응답 모델 SRM)과 동등하지만 SRM에서는 내부 변수가 멤브레인 전위 및 발화 임계값으로 해석되는 반면 GLM에서는 내부 변수는 스파이크가 g가 되기 전에 입력(및 최근의 출력 스파이크)의 순효과를 요약하는 추상적인 양입니다.마지막 ^[22][43]단계에서 기세가 꺾였다.

두 상태 마르코프 모델(노센슨 & 메시)

Nosson & Messer에^[61][62][63] 의한 스파이크 뉴런 모델은 외부 또는 약리적 자극의 ^[61][62][63]함수로서 스파이크를 발사할 가능성을 생성합니다.이 모델은 그림 4와 같이 수용체 층 모델과 스파이킹 뉴런 모델의 캐스케이드로 구성된다.외부 자극과 스파이킹 확률 사이의 연결은 다음 두 단계로 이루어집니다.우선 수용체 세포 모델은 원외 자극을 신경전달물질 농도로 변환하고, 다음으로 스파이킹 뉴런 모델은 신경전달물질 농도와 발화율(스파이킹 확률)을 연결한다.따라서, 스파이크 뉴런 모델은 그 자체로 ^[61][62][63]입력 단계에서 신경전달물질 농도에 의존합니다.

이 모델의 중요한 특징은 그림 5와 같이 자극 펄스에 대한 뉴런의 반응을 강조하는 특징적인 가장자리를 적은 수의 자유 매개변수를 이용하여 포착하는 뉴런 발화 속도 패턴의 예측이다.발화 속도는 신경 스파이크 발화에 대한 정규화된 확률과 세포에 의해 방출되는 신경 전달 물질의 전류에 비례하는 양으로 식별됩니다.기동 레이트의 표현은, 다음의 형식을 취합니다.

${\displaystyle R_{\text{fire}(t)=syslogfrac {P_{\text{spike}}(t;\Delta_{t}}}=[y(t)+]R_{0}]\cdot P_{0}(t)}$

어디에,

• P0은 뉴런이 "무장"되고 발사 준비가 될 확률이다.다음 미분방정식으로 구할 수 있습니다.

${\displaystyle\dot {P}}_{0}=sysy(t)+R_{0}+R_{1}\cdot P_{0}(t)+R_{1}}$

P0은 일반적으로 오일러 방법을 사용하여 재귀적으로 계산될 수 있지만, 자극 펄스의 경우 단순한 닫힌 형태 ^[61][70]식을 생성한다.

• y(t)는 모델의 입력이며, 주변 세포(대부분의 경우 글루탐산염)에 대한 신경전달물질 농도로 해석됩니다.외부 자극의 경우 수용체 층 모델을 통해 추정할 수 있습니다.

$\displaystyle y(t)\cdq g_{\text{gain}\cdot\cdot s^{2}(t)\rangle ,}$

(와트 또는 시간 단위당 기타 에너지로 주어진) 자극력의 짧은 시간 평균인${\displaystyle {}^{}}$ s $t$θ {\displaystyle $\langle$ s$^{2}(t)\rangle }$과 함께.

• R은₀ 뉴런의 고유 자발 발화 속도에 해당합니다.
• R은₁ 내화성 상태에서 뉴런의 회복 속도이다.

이 모델에 의한 기타 예측은 다음과 같습니다.

1) 여과되지 않은 측정에서 많은 뉴런의 집단에 의한 평균 유발 반응 전위(ERP)는 발화율과 ^[63]유사하다.

2) 다중 뉴런 활동에 의한 활동 전압의 분산은 발화율(Multi-Unit-Activity power,^[62][63] MUA라고도 함)과 유사하다.

3) 스파이크간 확률분포는 감마분포와 같은 함수를 가진다.^[61][70]

Nosson & Messer의^[61][62][63] 모델을 뒷받침하는 실험 증거

Nossonson & Messer의 모델 속성	레퍼런스	실험 근거 설명
청각 자극 펄스에 반응하는 발사 속도의 모양	[71][72][73][74][75]	발화율은 그림 5와 같은 모양을 하고 있다.
시각적 자극 펄스에 반응하는 발사 속도의 모양	[76][77][78][79]	발화율은 그림 5와 같은 모양을 하고 있다.
후각 자극 펄스에 반응하는 발사 속도의 형태	[80]	발화율은 그림 5와 같은 모양을 하고 있다.
체내 감각 자극에 반응하는 발사 속도의 모양	[81]	발화율은 그림 5와 같은 모양을 하고 있다.
신경전달물질 적용(대부분 글루탐산염)에 대한 반응으로 발생하는 발화율 변화	[82][83]	신경전달물질 적용에 따른 발화속도 변화(글루탐산염)
청각 자극 압력과 발화 속도 사이의 제곱 의존성	[84]	청각 자극 압력과 발화 속도 사이의 제곱 의존성(압력 제곱의 선형 의존성).
시각 자극 전계(볼트)와 발화 속도 사이의 제곱 의존성	[77]	시각 자극 전계(볼트) 사이의 제곱 의존성 - 시각 자극 전력과 발사 속도 사이의 선형 의존성.
스파이크 간 통계 정보(ISI)의 형상	[85]	ISI 모양은 감마 함수 모양과 유사하다.
ERP는 필터링되지 않은 측정에서 발화율과 유사합니다.	[86]	자극에 대한 반응의 평균 유발 반응 전위의 모양은 발사 속도와 유사하다(그림 5).
MUA 전력은 발화율과 유사합니다.	[63][87]	자극 펄스에 대한 세포외 측정의 경험적 분산의 모양은 발화 속도와 유사하다(그림 5).

약리학적 입력 자극 뉴런 모델

이 범주의 모형은 약리학적 자극과 관련된 실험에 대한 예측을 생성합니다.

시냅스 전송(Koch & Segev)

Koch와 ^[12]Segev의 모델에 따르면 개별 신경전달물질에 대한 뉴런의 반응은 고전적인 Hodgkin의 확장으로 모델링될 수 있다.표준 및 비표준 운동 전류를 모두 사용하는 Huxley 모델.네 가지 신경전달물질은 주로 CNS에 영향을 미친다. AMPA/카인산 수용체는 빠른 흥분 매개체이며, NMDA 수용체는 상당히 느린 전류를 매개한다.빠른_B 억제 전류는 GABA 수용체를 통과하며_A, GABA 수용체는 2차 G단백질 활성화 칼륨 채널을 통해 매개한다.이 조정 범위를 통해 다음과 같은 전류 역학을 생성합니다.

• ${\displaystyle I_{\mathrm {AMPA}}(t,V)=바 {g}_{\mathrm {AMPA}}\cdot [O]\cdot (V(t)-E_{\mathrm {AMPA}}}}}}$
• ${\displaystyle I_{\mathrm {NMDA}}(t,V)=바 {g}_{\mathrm {NMDA}}\cdot B(V)\cdot [O]\cdot (V(t)-E_{\mathrm {NMDA}}}}}$
• $\displaystyle I_{\mathrm {GABA_{A}} }(t,V)=바 {g}_{\mathrm {GABA_{A}}}\cdot([O_{1}]+[O_{2}])\cdot(V(t)-E_{\mathrm {Cl} })})$
• ${\displaystyle I_{\mathrm {GABA_{B}}=바 {g}}_{\mathrm {GABA_{B}}}\cdot {tfrac {[G]^{n}}+K_{\mathrm {d}}-CDOT(T)$

여기서 γ는 최대 전도도^[3][12](약 1S), E는 주어진 이온 또는 전달체(AMDA, NMDA, Cl 또는 K)의 평형 전위이며, [O]는 열려 있는 수용체의 분율을 나타낸다.NMDA는 B(V)에 의한 세포내 마그네슘 농도에 S자형으로 의존하는 마그네슘 블록의 영향이 크다.GABA의_B 경우 [G]는 G-단백질 농도이며_d, K는 칼륨 게이트와의 결합에서 G의 해리를 나타낸다.

이 보다 복잡한 모델의 역학은 실험적으로 잘 연구되어 매우 빠른 시냅스 증강과 우울, 즉 빠른 단기 학습이라는 측면에서 중요한 결과를 낳습니다.

Nossonson과 Messer에 의한 확률적 모델은 입력 단계에서 신경전달물질의 농도를 ^[61][62][63]출력 단계에서 신경전달물질을 방출할 확률로 변환한다.이 모델에 대한 자세한 설명은 위의 두 가지 상태 마르코프 모델 섹션을 참조하십시오.

HTM 뉴런 모델

HTM 뉴런 모델은 Jeff Hawkins와 Numenta의 연구자들에 의해 개발되었고, 원래 "Intelligence"라는 책에 기술된 계층적 시간 기억이라는 이론에 기초하고 있다.그것은 신경과학과 인간 뇌의 신피질에 있는 피라미드 뉴런의 생리와 상호작용에 기초하고 있다.

인공신경망(ANN)	신피질피라미달뉴런(생물뉴런)	HTM 모델 뉴런
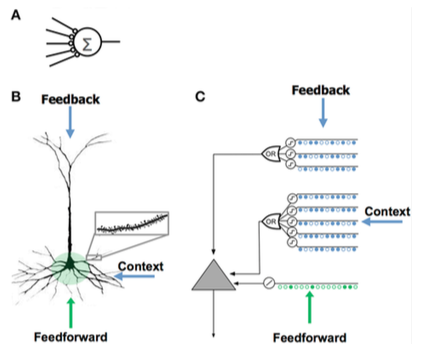
- 시냅스가 적다 - 덴드라이트 없음 - 총 입력 x 중량 - 시냅스 가중치를 수정하여 학습	- 수상돌기에 있는 수천 개의 시냅스 - 활성 수상돌기: 세포는 수백 가지의 독특한 패턴을 인식합니다. - 수지상 세그먼트에서 일련의 시냅스가 동시에 활성화되면 NMDA 스파이크와 소마에서 탈분극이 발생함 - 셀 입력원: 소마에 가까운 시냅스를 형성하고 활동 전위로 직접 이어지는 피드포워드 입력 NMDA 스파이크는 보다 원위부 기저부에서 발생한다. 소마를 탈분극시키는 원추상 수상돌기(보통 체세포 활동 전위를 생성하기에 충분하지 않음) - 새로운 시냅스를 성장시킴으로써 학습한다.	- 신피질층 2/3 및 5의 피라미드 세포에서 영감을 얻음 - 수천 개의 시냅스 - 활성 수상돌기: 세포는 수백 가지의 독특한 패턴을 인식합니다. - 일련의 시냅스를 가진 각 동시 검출기 어레이로 수상돌기와 NMDA 스파이크를 모델링합니다. - 새로운 시냅스의 성장을 모델링하여 학습

적용들

스파이킹 뉴런 모델은 신경 동토층 및 뇌-컴퓨터 인터페이스(예: 망막 보철물)^{[7][88][89][90]} 또는 인공 사지 제어 ^[91][92][93]및 감각의 맥락에서 신경 스파이크 트레인으로 인코딩하거나 디코딩해야 하는 다양한 애플리케이션에서 사용됩니다.어플리케이션은 이 문서의 일부가 아닙니다.이 주제에 대한 자세한 내용은 주요 기사를 참조하십시오.

인공뉴런 모델과 생물학적뉴런 모델의 관계

뉴런의 가장 기본적인 모델은 시냅스 무게 벡터를 가진 입력과 출력을 결정하는 뉴런 내부의 활성화 함수 또는 전달 함수로 구성됩니다.이것은 인공 뉴런에 사용되는 기본 구조이며, 신경 네트워크에서는 종종 다음과 같이 보입니다.

$(\displaystyle y_{i}=\varphi \left(\sum _{j}w_{ij}x_{j}\right)}$

여기서_i y는 i번째 뉴런의 출력_j, x는 j번째 입력 뉴런 신호, w는_ij 뉴런 i와 j 사이의 시냅스 무게(또는 연결 강도), θ는 활성화 함수이다.이 모델은 기계 학습 애플리케이션에서 성공을 거두었지만 입력과 출력의 시간 의존성이 부족하기 때문에 실제(생물학적) 뉴런에는 좋지 않은 모델이다.

입력이 t시에 켜지고 그 후에 일정하게 유지되면 생물학적 뉴런은 스파이크 트레인을 방출한다.중요한 것은 이 스파이크 트레인(spike train)은 규칙적이지 않지만 적응, 버스트 또는 초기 버스트에 이어 정기적인 스파이킹이 특징인 시간적 구조를 보인다는 것입니다.Adaptive Indequential Integrate-and-Fire 모델, 스파이크 응답 모델 또는 (선형) Adaptive Integrated-and-Fire 모델과 같은 일반화된 Integrated-Fire 모델은 이러한 신경 발화 ^[19][20][21]패턴을 포착할 수 있습니다.

게다가, 뇌의 신경 입력은 시간에 의존합니다.시간에 의존하는 입력은 복잡한 선형 및 비선형 필터에 의해 출력의 스파이크 트레인으로 변환됩니다.다시, 스파이크 응답 모델 또는 적응형 적분-발화 모델은 임의의 시간 의존 ^[17][18]입력에 대한 출력의 스파이크 트레인을 예측할 수 있게 하는 반면, 인공 뉴런 또는 단순 누출 적분-발화 모델은 그렇지 않다.

Hodkgin-Huxley 모델을 출발점으로 하면, 일반화된 통합 및 화재 모델을 단계별 단순화 절차에서 체계적으로 도출할 수 있습니다.이는 지수 적분-발화^[28] 모델과 스파이크 ^[49]응답 모델에 대해 명확하게 나타났다.

생물학적 뉴런을 모델링하는 경우, "무게" 및 "전달 함수"와 같은 추상화 대신 물리적 유사체가 사용된다.뉴런은 전하를 운반하는 이온을 포함한 물로 채워져 둘러싸여 있다.뉴런은 절연 세포막에 의해 결합되어 있으며 정전용량_m C를 결정하는 양쪽에 하전 이온의 농도를 유지할 수 있습니다.뉴런의 발화는 신경전달물질이 세포막의 이온 채널을 열게 할 때 일어나는 세포로의 이온 이동을 포함한다.이를 물리적 시간에 의존하는 전류 I(t)로 설명합니다.이와 함께 전압의 변화, 즉 셀과 그 주변 사이의 전기 전위 에너지 차이가 발생하는데, 이것은 때때로 셀의 길이를 이동하고 추가적인 신경 전달 물질의 방출을 유발하는 활동 전위라고 불리는 전압 스파이크를 야기하는 것으로 관찰됩니다.그러면 전압은 관심의 양이며 V(t)^[14]로_m 제공됩니다.

입력 전류가 일정하면 대부분의 뉴런은 일정한 시간 동안 적응하거나 일반 스파이크 트레인을 처음 버스트한 후에 방출합니다.정전류 I에 대한 정기 발화 주파수는 인공신경망의 전달 함수$\delta {\displaystyle }$(\$displaystyle \varphi)$에 해당하는 주파수-전류 관계로 설명된다.마찬가지로 모든 스파이킹 뉴런 모델에 대해 전달 함수$\delta {\displaystyle }$(\$displaystyle \varphi$})를$$ 수치적으로(또는 분석적으로) 계산할 수 있습니다.

케이블 이론 및 구획 모델

위의 결정론적 모델들은 모두 뉴런의 공간 구조를 고려하지 않기 때문에 점-뉴런 모델이다.그러나 덴드라이트는 입력을 ^[94][54]출력으로 변환하는 데 기여합니다.점 뉴런 모델은 세 가지 경우에 유효한 설명입니다.(i) 입력전류가 소마에 직접 주입되는 경우 (ii) 시냅스 입력이 주로 소마에 도달하는 경우(밀도는 다음에 소개하는 길이척도$\theta {\displaystyle }$(\$displaystyle\lambda)$로 정의)3) 시냅스가 덴드라이트에 도달하였으나 덴드라이트가 완전히 선형인 경우마지막 경우 케이블은 선형 필터로 기능합니다.이 선형 필터 특성은 스파이크 응답 모델과 같은 일반화된 통합 및 화재 모델의 공식에 포함될 수 있습니다.

필터 특성은 케이블 방정식으로 계산할 수 있습니다.

원통형 케이블 형태의 세포막을 생각해 봅시다.케이블의 위치는 x로 표시되고 셀막을 가로지르는 전압은 V로 표시됩니다.케이블의 특징은 단위 길이당 세로 ${\displaystyle {저항}_{}}$ r$${\$displaystyle r_{$l$$}, $막{\displaystyle {}_{}}$ ${\displaystyle {저항}_{}}$r m {\$displaystyle r_{$m}$$입니다.모든 것이 선형일 경우 전압은 시간의 함수에 따라 변화합니다.

${\displaystyle {r_{m}}{\frac ^{2}V}{\partial x^{2}}=c_{m}r_{m}{\frac {\partial t}+V}$

(19)

왼쪽에는 길이척도 ${\displaystyle 22{}_{}}$ ${\displaystyle {}^{}{}_{}r{}_{}}$ m / ${\displaystyle r_{}}$ l$${ $displaystyle$\ $displayda$^ { } = { r$$${\displaystyle {\_}_{}}$ { $m$} / { r$_$ { $l$$$} ${\displaystyle {}_{}}$ time time time ${\displaystyle =}$ c ${\displaystyle {\_}_{}}$ { $displaystyle$ \$displaystyle$= c _ {$}r$$$_ { $m$} r _ { m$$} } } a a a a a a a a a a a a 。케이블 방정식은 아마도 가장 잘 알려진 형태로 기술할 수 있습니다.

${\displaystyle \displayda ^{2}{\frac ^{2}V}=\frac {\frac {\partial t}+V}$

(20)

위의 케이블 방정식은 단일 원통형 케이블에 유효합니다.

선형 케이블 이론은 뉴런의 수지상 기둥을 나무의 가지와 같은 규칙적인 분기 패턴을 겪는 원통 구조라고 묘사합니다.단일 실린더 또는 전체 트리의 경우 베이스(트리가 셀 본체와 만나는 곳 또는 그러한 경계)에서의 정적 입력 컨덕턴스는 다음과 같이 정의된다.

${\displaystyle {\mathrm{Gi}}_{}}$ n ${\displaystyle {}_{}}$ ${\displaystyle G\frac{{}_{\mathrm{}}}{}}$tan ${\displaystyle \frac{\tanh }{}}$ ${\displaystyle \frac{(}{}}$ (${\displaystyle \frac{L}{}}$) + ${\displaystyle \frac{{}_{}}{}}$ ${\displaystyle \frac{L_{}}{}}$+ ( ${\displaystyle \frac{{}_{}{L}_{}}{}}$ / ${\displaystyle \frac{G{}_{}}{}}$ ${\displaystyle \frac{{}_{}}{}}$ ) ${\displaystyle \frac{\tanh (}{}}$ (${\displaystyle \frac{L}{}}$) \ $display style$ G_{$in$ }$= displayfrac${ $G_${ \ $infty$} \ $tanh$( $L$) + $G_ { 1$/ { $l }$

여기서 L은 길이, 지름 및 저항에 따라 달라지는 실린더의 전기토닉 길이입니다.단순한 재귀 알고리즘은 분기 수에 따라 선형적으로 확장되며 트리의 효과적인 컨덕턴스를 계산하는 데 사용할 수 있습니다.이것은 에 의해 주어집니다.

$디스플레이 스타일!G_{D}=G_{m}A_{D}\tanh(L_{D})/L_{D}}$

여기서_D A = δld는 총 길이 l의 나무의 총 표면적이고_D, L은 총 전기 토닉 길이이다.세포 본체 컨덕턴스가 G이고_S 단위 면적당 멤브레인 컨덕턴스가 G_md = G_m / A인 전체 뉴런에 대해, 우리는 다음과 같이 모든 나무와 소마 컨덕턴스를 합산함으로써 n개의 덴드라이트 나무에 대한 총 뉴런 컨덕턴스_N G를 구한다.

${\displaystyle G_{N}=G_{S}+\sum _{j=1}^{n}A_{D_{j}F_{dga_{j}}}$

G = GAF에_mdDdga 주목하여_D 실험적으로 일반 보정 인자 F를_dga 찾을 수 있다.

선형 케이블 모델은 닫힌 분석 결과를 제공하기 위해 여러 가지 단순화를 합니다. 즉, 수상돌기가 고정된 패턴에서 감소하는 쌍으로 분기해야 하며 수상돌기가 선형이라는 것입니다.구획^[54] 모델은 임의의 분기 및 길이뿐만 아니라 임의의 비선형성을 가진 임의의 트리 토폴로지를 허용합니다.기본적으로 비선형 덴드라이트의 이산화된 계산 구현입니다.

덴드라이트의 각 개별 조각 또는 구획은 임의의 길이 l 및 직경 d의 직선 실린더에 의해 모델화되며, 임의의 수의 분기 실린더에 고정 저항으로 연결된다.ih 실린더의 컨덕턴스 비율을_i B = G / G로_∞ 정의합니다_i. $여기$서 G${\displaystyle {\mathrm{}}_{}}$∞ ${\displaystyle {}_{}}$ ${\displaystyle \frac{{}^{}}{}}$ d ${\displaystyle \frac{{3\mathrm{}}^{}}{}}$/ ${\displaystyle \frac{2\sqrt{{}_{}}}{}}$ ${\displaystyle \frac{\sqrt{R_{}}}{}}$ i ${\displaystyle \frac{\sqrt{R_{}}}{}}$ m$${ \ $displaystyle G$_ { \ $infty$ } = t $tfrac${$pi$ d^ 3 / $2$} { $2 rtrt${ $R _${ 3 / { m $}$}}}}}}} R$$ 사이의_i 전류는 다음과 같습니다.다음과 같이 정규 동적_out,i B = B를_in,i+1 보정하여 격실 안팎의 컨덕턴스 비율에 대한 일련의 방정식을 구한다.

• ${\displaystyle B_{\mathrm {out},i}=sqrc {B_{\mathrm {in},i+1}/d_{i}}{3/2}}{\sqrt {R_{\mathrm {m},i}}}}{\sqrt {\mathrcrcrt {R}/{{{\m {\m}}}}}}{{\mathrm {in}}}}}}}}}}$
• ${\displaystyle B_{\mathrm {in},i}=param frac {B_{\mathrm {out},i}+\tanh X_{i}}{1+B_{\mathrm {out},i}}}}\tanh X_{i}}}}}$
• ${\displaystyle B_{\mathrm {out,par} = parfrac {B_{\mathrm {in,par1} }(d_{\mathrm {par} }){3/2}{\displayrt {R_{\mathrm {m {m {m} } } } / PARM {\parm}$

여기서 마지막 방정식은 지점에 있는 부모와 딸을 $다루고{\displaystyle {}_{}}$ ${\displaystyle {Xi}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle l\frac{{}_{}}{}}$ ${\displaystyle \frac{\sqrt{{}_{}}}{}}$ ${\displaystyle \frac{\sqrt{R_{}}}{}}$ i ${\displaystyle \frac{\sqrt{{}_{}{}_{}}}{}}$ R ${\displaystyle \frac{\sqrt{m_{}}}{}}${ $display style$ X _ { i } =$tfrac${ $l$_ { $i$} { \ $sqrt { 4R _${ $i$} }$$} } $。$이 방정식은 덴드 트리를 통해 얻을 때까지 반복할 수 있습니다.컨덕턴스비는 B입니다_in,stem.그러면 정적 입력을 위한 우리의 총 뉴런 전도율은 다음과 같이 주어진다.

${\displaystyle G_{N}=paramfrac {A_{\mathrm {soma}}}{R_{\mathrm {m,soma}}}+\sum _{\mathrm {in,stem},j}G_{\infty,j}.}$

중요한 것은 스태틱 입력은 매우 특별한 경우입니다.생물학에서 입력은 시간에 의존합니다.게다가, 수상돌기가 항상 선형인 것은 아니다.

구획 모델은 수상돌기를 ^[94][95]따라 임의의 위치에 위치한 이온 채널을 통해 비선형성을 포함할 수 있습니다.정적 입력의 경우 구획의 수를 줄이면서도(계산 속도를 높임) 두드러진 전기적 ^[96]특성을 유지하는 것이 때로는 가능하다.

뇌 작동 원리의 넓은 맥락에서 뉴런의 역할에 대한 추측

신경전달물질 기반 에너지 검출 방식

신경전달물질 기반 에너지 검출^[63][70] 방식은 신경조직이 Radar와 유사한 검출 절차를 화학적으로 실행함을 시사합니다.

그림 6과 같이, 이 추측의 핵심 아이디어는 신경전달물질 농도, 신경전달물질 생성 및 신경전달물질 제거율을 검출과제를 실행하는 데 중요한 양으로 고려하는 것이며, 측정된 전위를 특정 조건에서만 기능과 일치하는 부작용으로 참조하는 것이다.각 단계의 모든 목적.검출 방식은 에너지 검출기와 마찬가지로 신호 스쿼링, 시간 합계 및 임계값 스위치 메커니즘을 포함하지만 자극 에지 및 가변 메모리 길이(가변 메모리)를 강조하는 장치도 포함하기 때문에 레이더와 같은 "에너지 검출"과 유사하다.이 추측에 따르면 에너지 테스트 통계량의 생리학적 등가물은 신경전달물질 농도이며 발사속도는 신경전달물질 전류에 대응한다.이 해석의 장점은 전기생리학적 측정, 생화학적 측정 및 정신물리학적 결과를 연결할 수 있는 단위 일관성 있는 설명으로 이어진다는 것이다.

에서 검토한^[63][70] 증거는 기능성과 조직학적 분류 사이의 다음과 같은 연관성을 시사한다.

1. 자극 스쿼어링은 수용체 세포에 의해 수행될 가능성이 높다.
2. 자극 엣지 강조 및 신호 전달은 뉴런에 의해 이루어진다.
3. 신경전달물질의 시간적 축적은 아교세포에 의해 이루어진다.신경전달물질의 단기 축적은 일부 뉴런 유형에서도 발생할 수 있다.
4. 논리 스위칭은 글리얼 셀에 의해 실행되며, 신경전달물질 농도의 역치를 초과하여 이루어진다.이 문턱을 넘으면 신경전달물질 누출률의 변화도 동반된다.
5. 물리적 전체 또는 비운동 전환은 근육 세포에 기인하며 근육 주위의 특정 신경 전달 물질 농도 임계값을 초과한 결과입니다.

그림 6의 전기생리학 신호는 종종 기능 신호(신호력/신경전달물질 농도/근력)와 유사하지만 전기적 관찰이 해당 단계의 기능 목적과 다른 단계가 있다.특히, Nossonson 등은 글리아 역치 교차는 방사 전기생리학 신호에 비해 완전히 다른 기능적 연산을 가지며, 후자는 글리아 파괴의 부작용일 수 있다고 제안했다.

과학 및 엔지니어링 모델의 현대적 관점에 대한 일반적인 의견

• 위의 모델은 아직 이상화 단계입니다.수많은 수상돌기로 인해 발생하는 막 표면적 증가, 상온 실험 데이터보다 상당히 뜨거운 온도, 세포 내부 ^[12]구조의 불균일성을 보정해야 한다.관측된 특정 효과는 이러한 모형 중 일부에 적합하지 않습니다.예를 들어, 활동 전위 전파 중 세포막의 온도 순환(최소한의 순 온도 상승으로)은 전류가 흐를 때 에너지를 방출해야 하는 저항으로서 막 모델링에 의존하는 모델과 호환되지 않습니다.활동 전위 전파 중의 세포막의 일시적인 비후도 이러한 모델에서는 예측되지 않으며, 또한 이러한 비후로 인해 발생하는 변화하는 캐패시턴스 및 전압 스파이크도 이러한 모델에 통합되지 않습니다.불활성 가스와 같은 일부 마취제의 작용은 이러한 모델에도 문제가 있다.솔리톤 모델과 같은 새로운 모델은 이러한 현상을 설명하려고 시도하지만, 이전 모델보다 덜 개발되어 아직 널리 적용되지 않았다.
• 과학적 모델의 역할에 대한 현대적 견해는 "모든 모델은 잘못되었지만 일부는 유용하다"고 시사한다(Box and Draper, 1987, Gribbin, 2009; Paninski et al., 2009).
• 최근의 추측은 각 뉴런이 독립적인 임계값 단위의 집합으로 기능할 수 있다는 것을 암시한다.뉴런은 수지상 나무를 통해 막에 도달하는 신호의 기원에 따라 이방적으로 활성화될 수 있다고 제안된다.스파이크 파형은 ^[97]또한 자극의 원점에 따라 달라지는 것으로 제안되었다.

외부 링크

• 뉴런 다이내믹스: 단일 뉴런에서 네트워크 및 인지 모델까지(W. Gerstner, W. Kistler, R. Naud, L. Paninski, 케임브리지 대학 출판부, 2014).^[22]특히 6장부터 10장까지의 html 온라인 버전.
• 스파이킹 뉴런^[1] 모델 (W. Gerstner and W. Kistler, 캠브리지 대학 출판부, 2002)

「 」를 참조해 주세요.

• 결합뉴런
• 뇌 기능에 대한 베이지안 접근법
• 뇌-컴퓨터 인터페이스
• 자유 에너지 원리
• 신경 계산 모델
• 신경 부호화
• 신경 진동
• 활동 전위의 정량적 모델
• 스파이킹 뉴럴 네트워크

레퍼런스