활동 전위의 정량적 모델

신경생리학에서는 두 가지 기본적인 유형으로 분류되는 활동 전위의 수학적 모델이 몇 가지 개발되었습니다.첫 번째 유형은 실험 데이터를 정량적으로 모델링하는 것, 즉 전류와 전압의 측정을 정확하게 재현하는 것이다.유명한 호지킨-롤리고오징어에서 나온 축삭의 헉슬리 모델이 그러한 ^[1]모델의 예이다.H-H 모델은 질적으로 올바르기는 하지만, 두 가지 이온(나트륨과 칼륨)만 고려하기 때문에 모든 유형의 흥분성 막을 정확하게 설명하지는 않습니다. 각 모델은 전압에 민감한 채널을 하나만 가지고 있습니다.그러나 칼슘과 같은 다른 이온이 중요할 수 있으며 모든 ^[2]이온에 대한 채널은 매우 다양합니다.예를 들어, 심장 활동 전위는 전압에 민감한 칼슘 채널과 다양한 유형의 나트륨/칼륨 채널을 가진 막에서 어떻게 다른 형태의 활동 전위가 생성될 수 있는지를 보여줍니다.두 번째 유형의 수학적 모델은 첫 번째 유형을 단순화한 것입니다. 목표는 실험 데이터를 재현하는 것이 아니라 신경 회로에서 활동 전위의 역할을 질적으로 이해하는 것입니다.그러한 목적을 위해, 상세한 생리학적 모델은 불필요하게 복잡할 수 있으며 "나무의 숲"을 모호하게 할 수 있다.FitzHugh-Nagumo 모델은 이 클래스의 전형적인 모델로,^[3] 교란 동작에 대해 종종 연구됩니다.교락은 자연에서, 예를 들어 활동 전위의 ^[4]폭발에 의해 조정되는 반딧불이의 동기화된 조명에서 흔히 관찰된다. 교락은 개별 ^[5]뉴런에서도 관찰될 수 있다.두 가지 유형의 모델은 일부 자동 반사 작용을 ^[6]담당하는 중앙 패턴 발생기와 같은 작은 생물학적 신경망의 동작을 이해하기 위해 사용될 수 있다.이러한 네트워크는 ^[7]포식자를 피하기 위해 호흡이나 빠른 수영과 같은 근육 수축을 조정하는 데 사용되는 복잡한 시간적 행동 전위 패턴을 생성할 수 있다.

호지킨헉슬리 모형

1952년 Alan Lloyd Hodgkin과 Andrew Huxley는 축삭막의 ^[1][8]실험 전압 클램프 데이터를 맞추기 위해 일련의 방정식을 개발했습니다.이 모델은 막 캐패시턴스 C가 일정하다고 가정합니다. 따라서 총 막간 전류_tot I에 따라 막간 전압 V가 변화합니다.

${\displaystyle C{\frac {dV}{dt}}}=I_{\mathrm {tot} = I_{\mathrm {ext} } + I_{\mathrm {Na} } + I_{\mathrm {K} } + I_{\mathrm {L} } }$

여기서_Na I, I_K 및_L I는 각각 로컬 나트륨 채널, 칼륨 채널 및 "누출" 채널(캐치 올)을 통해 전달되는 전류입니다.초기 용어_ext I는 덴드라이트 또는 과학자의 전극에서 흥분성 시냅스 후 전위와 같은 외부 소스로부터 도달하는 전류를 나타냅니다.

이 모델은 또한 주어진 이온 채널이 완전히 열리거나 닫혔다고 가정합니다. 닫혔을 경우 전도도는 0인 반면, 열린 경우 전도도는 일정한 값 g입니다.따라서, 이온 채널을 통과하는 순 전류는 두 가지 변수에 의존합니다: 채널이 열릴_open 확률 p와 이온의 평형 전압 V - V로부터의_eq 전압 차이. 예를 들어, 칼륨 채널을 통과하는 전류는 다음과 같이 기록될 수 있습니다.

$\displaystyle I_{\mathrm {K}=g_{\mathrm {K}}\left(V-E_{\mathrm {K}}\right)p_{\mathrm {open,K}}}}$

옴의 법칙과 맞먹습니다.정의에 따르면, 막 통과 전압이 이온의 평형 전압과 같을 때(V_K = E일 때) 순 전류는_K 흐르지 않습니다.

데이터를 정확하게 맞추기 위해 Hodgkin과 Huxley는 각 이온 채널 유형에 여러 개의 "게이트"가 있다고 가정했다. 따라서 모든 게이트가 열려 있고 닫혀 있을 때만 채널이 열려 있다고 가정했다.또한 게이트가 개방될 확률은 다른 게이트가 개방되는 것과 무관하다고 가정했다. 이 가정은 나중에 비활성화 ^[9]게이트에 대해 검증되었다.호지킨과 헉슬리 4대 문중을 가진 것으로, pn 하나의 확률은 공개되는 것 의미, 전체 채널 중 전면 개방은 4명 확률의 제품 즉, popen, K)n4의 확률이voltage-sensitive 칼륨 채널 모델을 했습니다.마찬가지로,voltage-sensitive 나트륨 채널의 확률 월을 본떠서 만들어졌다ree 확률 m의 유사한 게이트와 불활성화와 관련된 확률 h의 네 번째 게이트. 따라서 p_{open, Na} = mh³.각 관문에 대한 확률은 1차 동력을 따르는 것으로 가정한다.

${\displaystyle {frac {dm} {dt}}=-{\frac {m-m_{\mathrm {eq}}}{\frac _{m}}}$

여기서 평형값_eq m과 완화시간 상수 θ는_m 멤브레인 전체의 순간전압 V에 의존한다.V가 θ보다_m 느리게 변화하는 경우 m 확률은 항상 평형값_eq m과 거의 동일하지만, V가 더 빨리 변화하면 m은 m에_eq 뒤처진다.Hodgkin과 Huxley는 전압 클램프 데이터를 적합시킴으로써 이러한 평형 값과 시간 상수가 온도 및 막 통과 ^[1]전압에 따라 어떻게 변화하는지 모델링할 수 있었다.공식은 복잡하고 전압과 온도에 따라 기하급수적으로 달라집니다.예를 들어 나트륨 채널 활성화 확률 h의 시간 상수는 섭씨 온도 θ에 따라 3으로^{(θ−6.3)/10} 변화하고 전압 V는 다음과 같이 변화한다.

${\displaystyle {\frac {1}{\frac _{h}}=0.07e^{-V/20}+{\frac {1}{1+e^{3-V/10}}}.}$

요약하자면, 호지킨은...헉슬리 방정식은 4개의 독립 변수(막간 전압 V 및 확률 m, h 및 n)^[10]에서 복잡한 비선형 상미분 방정식입니다.이 방정식의 일반적인 해는 아직 발견되지 않았다.이러한 비선형 동적 시스템을 연구하기 위한 더 큰 야망은 없지만 일반적으로 적용할 수 있는 방법은 고정점 ^[11]부근에서의 동작을 고려하는 것이다.이 분석에 따르면 호지킨은...헉슬리계는 자극전류_ext I이 점차 증가함에 따라 안정정지 상태에서 폭발진동으로 이행하고,^[12] 자극전류가 더욱 증가함에 따라 축삭은 다시 안정정지 상태가 된다.Hodgkin에 의해 예측된 축삭의 질적 행동 유형에 대한 보다 일반적인 연구 -Huxley 방정식도 수행되었습니다.^[10]

피츠휴-나구모 모형

호지킨의 복잡성 때문에...헉슬리 방정식은 질적으로 유사한 ^[3][13]행동을 보이는 다양한 단순화가 개발되었습니다.FitzHugh-Nagumo 모델은 이러한 단순화된 시스템의 ^[14][15]전형적인 예입니다.터널 다이오드에 근거해, FHN 모델은 2개의 독립 변수만을 가지고 있지만, 완전한 Hodgkin과 유사한 안정성 동작을 보인다.헉슬리 ^[16]방정식방정식은

${\displaystyle C{\frac {dV}{dt}}=I-g(V),}$

$\displaystyle L{\frac {dI}{dt}}=E-V-RI}$

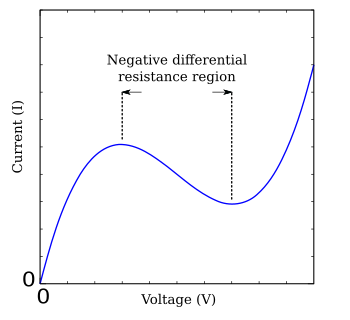
여기서 g(V)는 음의 기울기 영역이 중앙에 있는 전압 V의 함수이며, 측면은 최대값과 최소값으로 구분됩니다(그림 FHN).FitzHugh-Nagumo 모델의 많은 연구가 이루어진 간단한 사례는 Bonhoffer-van der Pol 신경 모델이며, 이것은^[17] 방정식으로 설명된다.

$({displaystyle C{\frac {dV}{dt}}=I-\epsilon \leftfrac {V^{3}}:{3}}-V\right})$

$\displaystyle L{\frac {dI}{dt}}=-V}$

여기서 계수 θ는 작은 것으로 가정한다.이 방정식은 2차 미분 방정식으로 결합될 수 있다.

${\displaystyle C{\frac {d^2}V}{dt^{2}}+\epsilon \left(V^{2}-1\right){\frac {dV}+{\frac {V}{L}}=0.}$

이 반데르폴 방정식은 비선형 동적 시스템의 수학에 많은 연구를 자극했다.활동 전위의 FHN과 반데르폴 모델을 실현하는 Op-amp 회로는 키너에 ^[18]의해 개발되었다.

호지킨의 잡종...Huxley와 FitzHugh-Nagumo 모델은 1981년 Morris와 Lecar에 의해 개발되어 따개비의 ^[19]근섬유에 적용되었습니다.바나클의 생리학에 부합하는 Morris-Lecar 모델은 Hodgkin의 전압 게이트 나트륨 전류를 대체한다.전압 의존형 칼슘 전류를 사용하는 Huxley 모델.불활성화(h 변수 없음)가 없고 칼슘 전류가 순간적으로 평형을 이루므로 시간 의존 변수인 트랜스막 전압 V와 칼륨 게이트 확률 n 두 개만 있습니다.이 모델의 폭발, 교란 및 기타 수학적 특성이 상세하게 ^[20]연구되었다.

동작 전위의 가장 단순한 모델은 "플래시 앤 필" 모델(일명 "적분 앤 파이어" 모델이라고도 함)로, 입력 신호가 임계값에 도달할 때까지 합산되어 펄스를 실행하고 합계를 0(플래시)^[3][21][22]으로 재설정합니다.이 모든 모델은 신경계에서 ^[3]흔히 관찰되는 교란 현상을 나타낼 수 있다.

세포외 전위 및 전류

위의 모델들은 막의 단일 패치에서 막 통과 전압과 전류를 시뮬레이션하는 반면, 다른 수학적 ^[23]모델들은 뉴런을 둘러싼 이온 용액 내의 전압과 전류와 관련이 있습니다.이러한 모델은 세포 내 ^[24]기록을 가능하게 하는 유리 피펫 전극이 발명되기 전에 흔했던 세포 외 전극의 데이터를 해석하는 데 도움이 됩니다.세포 외 매질은 일반적인 등방성 이온 용액으로 모델링될 수 있습니다. 이러한 용액에서 전류는 옴의 법칙의 연속체 형태에 따라 전계 라인을 따릅니다.

${\displaystyle \mathbf {j} =\display \mathbf {E} }$

여기서 j와 E는 각각 전류 밀도와 전계를 나타내는 벡터이고 θ는 전도율이다.따라서, j는 맥스웰 방정식을 사용하여 구할 수 있는 E로부터 구할 수 있다.맥스웰 방정식은 이온 농도가 자기 효과가 중요하기 때문에 (빛의 속도에 비해) 너무 느리게 변화하기 때문에 상대적으로 단순한 정전학 문제로 축소될 수 있다.어떤 세포 외 지점 x에서의 전위 δ(x)는 그린의 식별을^[23] 사용하여 해결할 수 있다.

${\displaystyle \phi (\mathbf {x}) = flac {1} {4\pi \pi } } } \point _ {\mathrm {pair} {\frac n} {\frac {1} {\left \mathbf {x} - {\xi} } {\} {\} {\} {\} {\} } {\point }xi }})\right]dS}$

$(\displaystyle\boldsymbol\$xi$$})는$$ 막의 위치이고 δ와_insideinside δ는 막 내의 전도도와 퍼텐셜이며$$δ와_{outsideoutside} δ는 막 바로 바깥쪽에 있는 해당 값이다.따라서 막상의 이러한 δ값 및 δ값을 바탕으로 세포외전위 δ(x)를 임의의 위치 x에 대해 계산할 수 있으며, 이 ^[25]전위장으로부터 전장 E 및 전류밀도 j를 계산할 수 있다.

「 」를 참조해 주세요.

• 생물학적 뉴런 모델
• GHK 전류 방정식
• 신경 계산 모델
• 염분 전도
• 바이오 일렉트로닉스
• 케이블 이론

레퍼런스

추가 정보

• Glass L, Mackey MC (1988). From Clocks to Chaos: The Rhythms of Life. Princeton, New Jersey: Princeton University. ISBN 978-0-691-08496-1.