린들러 좌표

상대론적 물리학에서, 하이퍼볼릭적으로 가속된 기준 프레임의^{[H 1][1]} 좌표는 플랫 민코프스키 스페이스타임의 일부를 나타내는 중요하고 유용한 좌표 차트를 구성한다.^[2][3][4][5] 특수상대성이론에서 균일하게 가속되는 입자는 쌍곡선 운동을 하는데, 이 운동을 위해 균일하게 가속되는 기준 프레임을 적절한 기준 프레임으로 선택할 수 있다. 이 고압적으로 가속된 프레임의 현상은 동질적인 중력장에서 발생하는 효과와 비교할 수 있다. 평탄한 시간 동안의 가속도에 대한 일반적인 개요는 가속(특수 상대성) 및 적절한 기준 프레임(평탄한 시간)을 참조하십시오.

이 글에서 빛의 속도는 c = 1, 관성 좌표는 (X, Y, Z, T), 쌍곡 좌표는 (x, y, z, t)로 정의된다. 이러한 쌍곡 좌표는 가속된 관찰자의 위치에 따라 크게 두 가지 변형으로 구분할 수 있다. 만약 관찰자가 위치 X = 1/α에 시간 T = 0에 위치한다면(결합 가속도계에 의해 측정된 일정한 적절한 가속도로 α), 쌍곡 좌표는 흔히 해당 린들러 측정계와 함께 린들러 좌표라고 불린다.^[6] 관찰자가 위치 X = 0에서 시간 T = 0에 위치하는 경우 쌍곡 좌표를 Møler 좌표^[1] 또는 해당 Kottler-Møler 측도계와의 Kottler-Møler 좌표라고 부르기도 한다.^[7] 쌍곡선 움직임에서 관찰자와 종종 관련된 대체 차트는 때때로 Lass 좌표라고 불리는 Radar 좌표를^[8] 사용하여 얻는다.^[9][10] 라스 좌표뿐만 아니라 코틀러-몰러 좌표도 린들러 좌표로 표시된다.^[11]

역사와 관련하여, 그러한 좌표는 특수상대성이 출현한 직후에 도입되었는데, 이때 쌍곡운동의 개념과 함께 (완전하거나 부분적으로) 연구되었다. 평평한 민코프 스키 블랙 홀에 알버트 아인슈타인에 의한 관계에서 막스 보른(1909년),(1907년, 1912년)[H 2].[H1]아르놀트 조머 펠트(1910년)[H 3]막스 폰 라우에 헨드릭 로런츠(1911년)[H4]프리드리히 Kottler(1914년)[H6]볼프강 파울리(1921년),(1913년)[H5].[H 7]칼 Bollert(1922년),.[H 8]스체판 Mohorovičić(1922년),.[H9]조르주 르메트르(1924년),.[H10]아인슈타인 &, 나단 로젠(1935년)[H 2]기독교 버섯 버섯(1943년, 1952)[H11].Itz Rohlich ^[12](1963년), Harry Lass (1963년),^[13] 그리고 볼프강 린들러 (1960년, 1966년)에 의한 일반 상대성의 평평한 공간과 곡선의 공간 시간 둘 다와 관련된다.^[14][15] 자세한 내용 및 출처는 § History를 참조하십시오.

린들러 프레임의 특성

$X{\displaystyle }$ ${\displaystyle X}$에서 적절한$$ 가속도 $\alpha {\displaystyle }$ ${\displaystyle \alpha }$ -방향에 적절한 시간 $\tau {\displaystyle }$ ${\displaystyle \tau }$과 신속도 $\alpha {\displaystyle }$ α ${\displaystyle \tau }$ ${\displaystyle \alpha \tau}$의 함수로써 일정하게 적절한 가속도 α를 가지는 쌍곡선(worldline bodyproundervolline)을 제공할^[16] 수 있다$$.

${\displaystyle T=x\sinh(\alpha \tau ),\quad X=x\cosh(\alpha \tau )}$

어디 x초기 조향 순간을 1/α{\displaystyle x=1/\alpha}과α τ{\displaystyle \alpha \tau}은 변덕스럽다,worldline은 쌍곡선을 연상시켜 X2− T2cmx2{\displaystyle X^{2}-T^{2}=x^{2}}. Sommerfeld[H 3][17]은 방정식 정의하여 재해석 될 수 있다는 것을)V로{\displaystyle)}일정하다한ariablend $\alpha {\displaystyle }$ ${\displaystyle \tau }$ ${\displaystyle \tau }$은(는) 일정하게 나타나기$$ 때문에, 이는 교감하는 관찰자가 측정한 쌍곡선 운동으로 신체의 동시적인 "휴식 형태"를 나타낸다. $\tau {\displaystyle }$= ${\displaystyle t}$ ${\displaystyle \tau =t}$을(를) 설정하여 관찰자의 적절한 시간을 전체 하이퍼볼릭 가속 프레임의 시간으로 사용함으로써 관성 좌표와 쌍곡 좌표 사이의 변환 공식은 결과적으로 다음과 같다$.$^[6][9]

${\displaystyle T=x\sinh(\alpha t),\quad X=x\cosh(\alpha t),\quad Y=y,\quad Z=z}$

(1a)

역행하여

${\displaystyle t={\frac {1}{\alpha }}\operatorname {artanh} \좌측({\frac {T}{X}\\오른쪽)\quad x={\x^{2}-T^{2}}},\quad y=Y,\quad z=Z}$

구별하여 민코스키 미터법 $d{\displaystyle }$ s ${\displaystyle {2\mathrm{}}^{}}$=${\displaystyle }$- d ${\displaystyle {T\mathrm{}}^{}}$ 2${\displaystyle {}^{}}$+ d ${\displaystyle X}$ ${\displaystyle {}^{}}$+ ${\displaystyle d}$ ${\displaystyle Y}$ ${\displaystyle {2\mathrm{}}^{}}$ +${\displaystyle {}^{}}$d Z ${\displaystyle {2\mathrm{}}^{}}$ ${\$2}+dX^{2}+d$}+d$}+d}+d$Y^{2}+dZ^{2$ 하이퍼볼릭 가속 프레임의 메트릭은 다음과 같다.

${\displaystyle ds^{2}=-(\dvx x)^{2}+dx^{2}+dy^{2}+dy^{2}+dz^{2}}$

(1b)

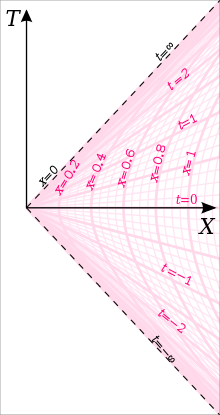
이러한 변환은 린들러 관찰자를 린들러 좌표에서 "정지 상태"인 관찰자로 정의한다. 즉, 일정한 x, y, z를 유지하고 시간이 경과함에 따라 변화되는 t만을 유지하는 것이다. 그 좌표는 지역 0에서 <, X<>∞,− X<T>X{0<\displaystyle, X<,\infty ,\, -X<, 유효하다.T<, X}, 만약 α{\displaystyle \alpha}그 적절한 시간에 정의되어 있는 Rindler 관찰자의 적절한 가속도(그 쌍곡선을 따라)=1/α{\displaystyle x=1/\alpha})를 나타내는 자주 Rindler 웨지라고 불린다. 린들러 좌표 시간과 같다. 이 세계선을 유지하려면, 린들러 관측자가 ${\displaystyle \mathrm{x}}$= 0 ${\displaystyle x=0}($린들러 수평선)에 더 가까운 적절한 가속도로 관찰자가 일정한 적절한 가속도로 가속해야 한다. All the Rindler observers are instantaneously at rest at time ${\displaystyle T=0}$ in the inertial frame, and at this time a Rindler observer with proper acceleration ${\displaystyle \alpha _{i}}$ will be at position ${\displaystyle X=1/\alpha _{i}}$ (really ${\display$$스타일 X=c^{2}/\alpha _{i$ ${\displaystyle \mathrm{그러나}}$ $우리$는 c${\displaystyle }$= 1 ${\displaystyle c=1})$의 단위를 가정하는데, 이는 또한 린들러 좌표에서 그 관측자가 린들러 수평선으로부터 일정한 거리인 것이다. 모든 린들러 관찰자가 시계를 $T{\displaystyle }$ =${\displaystyle 0}$ ${\displaystyle T=0$에서 0으로 설정한 경우, 린들러 좌표계를 정의할 때 우리는 린들러 관찰자의 적절한 시간을 린들러 좌표에서$$ $좌표시간{\displaystyle }$ t$${\$displaystyle$t}과 동일하게 선택할 수 있으며, 이 관찰자의 적절한 가속도는 $\alpha$의 값을 정의한다.$$위의$$ $[\displaystyle \alpha }$ (Rindler 지평선에서 다른 거리에 있는 다른 Rindler 관찰자의 경우, 좌표 시간은 적절한 시간의 일정 배수와 동일할 것이다.)^[18] 적절한 시간이 좌표 시간과 일치하는 린들러 관찰자가 적절한 가속도 ${\displaystyle \mathrm{\alpha }}$= 1 ${\displaystyle \alpha =$1}을(를$)$ 갖는 사람이 되도록 린들러 좌표계를 정의하는 것은 일반적인 관례로, $\alpha {\displaystyle }$ ${\displaystyle \alpha$ }을$($를) 방정식에서 제거할 수 있다$$.

$c{\displaystyle }$= ${\displaystyle 1}$ ${\displaystyle c=1}$에 대해 위의 방정식이 단순화되었다$.$ 검증되지 $않은{\displaystyle }$방정식은 가속 α {\$displaystyle \$alpha }을(를) 고려할 때 Rindler Horizon 거리를 찾는데 더 편리하다$.$

${\displaystyle {\begin}t&={\frac {c}{\alpha }}\operatorname {artanh} \좌측({\frac {cT}{X}\우측)\;{\overset {X\,\g \}{}}}}}}}{prac {c^2}}}{{\alpha X}\\X&\약 {\frac {c^{2}}}{\alpha t}\;{\overset {T\,\closure,t}{\c^{2}}:{\frac{c^{}}{\alpha }}}}}}$

The remainder of the article will follow the convention of setting both ${\displaystyle \alpha =1}$ and ${\displaystyle c=1}$, so units for ${\displaystyle X}$ and ${\displaystyle x}$ will be 1 unit ${\displaystyle =c^{2}/\alpha =1}$. Be mindful that setting ${\displaystyl$$e \alpha$ =1$}광초/$초는$$ α² = ${\displaystyle$\ \ $=$1}광년$$$/$년² 설정과 매우 다르다. $c{\displaystyle }$= ${\displaystyle 1}$ ${\displaystyle c=1}$단위를 선택하더라도 적절한 가속도 $\alpha {\displaystyle }$ ${\displaystyle \alpha }$의 크기는 선택 단위에 따라 달라진다$$. 예를 들어 거리에 광년 단위(${\displaystyle }$ ${\displaystyle$ $X$$}$ 또는$$ $x{\displaystyle }$ ${\displaysty$ x$\})$ 및 시간(${\displaystyle }$ ${\displaystystystytytytytytytytytytype$ T$}$ 또는$$ T})T{\displaystyle지}음, 이거는 동안 우리가 아마 시간에 거리 light-seconds,(X{X}\displaystyle 또는 x{\displaystyle x}), 초의 단위를 사용한다,(T{\displaystyle T}이나 몸 상태를{\displaystyle t}), 이 것을 의미할 것이다=1α{\displaystyle \alpha =1}빛 year/year2, 약 9.5meters/second2에 동등한 것, 의미할 것이다.${\displaystyle \alpha }$= ${\displaystyle 1}$ ${\displaystyle \alpha$=1$}광초$/초² 또는 299 792 458m/초²).

변환 수식의 변형

페르미 좌표 또는 적절한 좌표를 도출할 수 있는 해당 페르미-워커 테트라드가 공식화된 경우 변환 공식의 보다 일반적인 파생이 제시된다.^[19] 이러한 좌표의 원점 선택에 따라 메트릭을 도출할 수 있으며, $점{\displaystyle }$ x ${\displaystyle$ $dt_{0$$}$에서 원점 ${\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$displaystyle $dt_$0}과$$ d$$ {\$displaystyle$ dt$}$ 사이의 시간 확장 및 좌표 광속 ${\displaystyle dx}$ / ${\displaystyle d}$ $displaystystyledx$/ $dt }$을 도출할 수 있다($$이 변수).빛의 속도는 특수 상대성 이론과 모순되지 않는데, 이는 관성 좌표에서는 일정하게 유지되는 반면, 사용된 가속 좌표의 인공물이기 때문이다. 또한 Fermi 좌표 대신 Radar 좌표를 사용할 수 있다. 레이더 좌표는 광신호를 사용하여 거리를 결정함으로써 얻을 수 있다(거리 개념 섹션 참조), 미터법, 시간확장 및 빛의 속도가 좌표에 더 이상 의존하지 않는다 – 특히 빛의 좌표 속도는 빛의 속도와 동일하다.${\displaystyle \mathrm{관성}}$ ${\displaystyle \mathrm{프레임}}$의${\displaystyle }$(c$$ = 1 ) ${\displaystyle(c=1):$

${\displaystyle }$$T{\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle T=0}$의 X ${\displaystyle X}$	빛의 변환, 미터법, 시간확장 및 조정 속도
$[\displaystyle X=0}$	코틀러-몰러 좌표[H 12][20][21][22]
	${\displaystyle {\reason{array}{c}{\reason{aigned}}T&=\frac(x+{\frac{1}{\alpha }}\오른쪽)\sinh(\alpha t)\\x&=\좌(x+{\fraca{1}{\alpha }\오른쪽)\cosh(\alpha t)-{\frac {1}{\frapa }\}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\Y&=y\\\Z&}z\ended}&#{\begin}t&={\frac {1}{\frac }}{\frac {T}{X+{\frac {1}{\alpha }}}\right)\\x&={\sqrt {\frac {1}{\\frac {1}{\alpha }}}}^{2}-{\frac {1}{\alpha }}\y&=}^{2}-{\frac {1}{\alpha }\y&=Y\\\z&=Z\end{array}}$ (2a) ${\displaystyle ds^{2}=-(1+\nfs x){}^{2}dt^{2}+dx^{2}+dy^{2}+dy^{2}+dz^{2}}$ (2b) ${\displaystyle dt=(1+\cHB x)dt_{0},\qquad {\frac {dx }{dt }=1+\cHB x}$ (2c)
	린들러 좌표[23][24][18]
${\displaystyle X={\frac {1}{\alpha }}$	${\displaystyle {\reason{array}{c}{\reason{aigned}}T&=x\sinh(\alpha t)\\X&=x\cosh(\alpha t)\\\\Y&=y\\\Z&=z\ended}&{\begin}t&={\frac{1}{\frac{1}{\alpha }}\operatorname {artanh}{\frac {T}\x&={\sqrt{X^{2}-T^}}}\y&=}}\y&=Y\\\z&=Z\end{array}}$ (2d) ${\displaystyle ds^{2}=-(\dvx x)^{2}+dx^{2}+dy^{2}+dy^{2}+dz^{2}}$ (2e) ${\displaystyle dt=\dt_{0},\qquad {\frac {dx}{dt }}=\dmx x}$ (2f)
	레이더 좌표(Lass 좌표)[25][26][8][9]
${\displaystyle X={\frac {1}{\alpha }}$	${\displaystyle {\reason{array}{c}{\reason{aigned}}T&={\frac {1}{\alpha }}{\alpha ^{\alpha x}\sinh(\alpha t)\\x&={\frac {1}{\alpha }}{\alpha x}\cosh(\alpha t)\\\\\\\\Y&=y\\Z&=z\end{aligned}}&{\begin{aligned}t&={\frac {1}{\alpha }}\operatorname {artanh} {\frac {T}{X}}\\x&={\frac {1}{2\alpha }}\ln \left[\alpha {}^{2}\left(X^{2}-T^{2}\right)\right]\\y&=Y\\\z&=Z\end{array}}$ (2g)
	${\displaystyle ds^{2}=e^{2\filename x}\왼쪽dt^{2}+dx^{2}}\오른쪽)+dy^{2}+dz^{2}}$ (2h) ${\displaystyle dt=e^{\put x}dt_{0},\qquad {\frac {dx }{dt }}=1}$ (2i)

린들러 관찰자

$c{\displaystyle }$= ${\displaystyle 1}$ ${\displaystyle c=1}$및$$ ${\displaystyle \mathrm{\alpha }}$= 1 ${\displaystyle \alpha =$1}을$($를) 갖는 새 차트(1)에서는 코프레임 필드를 선택하는 것이 자연스럽다$.$

${\displaystyle d\dma ^{0}=x\,dt,\;d\d\d\ma ^{1}=dx,\;d\d\ma ^{2}=dy,\;d\d\ma ^{3}=dz}$

이중 프레임 필드가 있는

${\displaystyle {\vec{e}_{0}={\frac {1}{x}\c}\{1}\;{\vec{e}}}=\{x}}=\\\\vec{e}}=\{y}}=\;\vec {e_{3}=\}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}\{{{{{{{{{{{{$

이것은 각 이벤트의 접선 공간(Rindler 차트에서 다루는 영역, 즉 Rindler 쐐기)에서 로컬 로렌츠 프레임을 정의한다. 타임라이크 단위 벡터 필드 $e{\displaystyle {\stackrel{}{}}_{}}$→ ${\displaystyle 0_{\mathrm{}}}$ ${\$의 일체형 곡선은 타임라이크 일치성을 부여하며$$, 린들러 관찰자라고 불리는 관찰자 가족의 세계 라인으로 구성된다. 린들러 차트에서 이러한 세계선은 수직 좌표선 $x{\displaystyle }$= ${\displaystyle {x\mathrm{}}_{}}$ 0${\displaystyle {}_{}}$ y${\displaystyle }$= ${\displaystyle {y\mathrm{}}_{}}$ = 0${\displaystyle {}_{}z}$ = ${\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$x=$x_{0},\;y={0},\;z=z_{0}}}$로 나타난다$.$ 위의 좌표 변환을 사용하면 원래 데카르트 차트에서 쌍곡선과 일치한다는 것을 알 수 있다.

로렌츠 다지관의 모든 시간적 결합과 마찬가지로 이 결합은 키네마틱 분해를 가진다(레이쇼우두리 방정식 참조). 이 경우 린들러 관찰자의 일치의 확대와 다양성은 사라진다. 확장 시제의 소멸은 우리의 관찰자 각자가 그의 이웃들과 일정한 거리를 유지한다는 것을 의미한다. vorticity tensor의 소멸은 우리 관찰자들의 세계선이 서로 뒤틀리지 않고 있다는 것을 암시한다; 이것은 일종의 "swirling"의 국지적인 부재다.

각 관찰자의 가속 벡터는 공변량 파생 모델에 의해 주어진다.

${\displaystyle \epla_{\vec{e}_{0}{\vec{e}}}={\frac {1}{x}}{\vec{e}_{1}:{1}}}}}$

즉, 각 린들러 관찰자는${\displaystyle {\mathrm{}}_{}}$∂ ${\displaystyle x_{}}$ ${\$ 방향으로 가속하고$$ 있다. 개별적으로 말하면, 각 관찰자는 사실 이 방향에서 일정한 크기를 가지고 가속하고 있기 때문에, 그들의 세계선은 유클리드 기하학에서 일정한 경로 곡률의 곡선인 원의 로렌츠 유사점이다.

Rindler 관찰자들은 vorticity가 없기 때문에, 그들은 또한 초지직교적인 얼굴이다. 직교 공간 $과플릭$은${\displaystyle {}_{}}$ = ${\displaystyle {t\mathrm{}}_{}}$0 {\$displaystyle t=t_{$0}}이다$.$ 이는 Rindler 차트에서 수평 반평면으로 나타나고 $T{\displaystyle }$= ${\displaystyle \mathrm{X}}$= 0 ${\displaystyle T=X=0}$을(를$$) 통과하는 반평면으로 나타난다(위의 그림 참조). )dt는 다음 선소에서 0{\displaystyle dt=0}을 설정하면, 우리는 이, d σ 2)보통의 유클리드 기하학 d고 있는 2+d는 y2+dz2, ∀)>;0,∀는 y, z{\displaystyle d\sigma ^{2}=dx^{2}+dy^{2}+dz^{2},\, \forall x>, 0,\forall y,z}. 그러므로 Rindler 차트에서 공간 영역 좌표는 매우 단순한 있다.int린들러 관찰자들이 상호 정지되어 있다는 주장과 일치한다. 우리는 이 글에서 조금 늦게 린들러 관찰자들의 경직성 속성으로 돌아갈 것이다.

"극복성" 특성

더 작은 상수 x 좌표를 가진 린들러 관찰자들은 따라가기 더 어려워지고 있다는 점에 유의한다. 뉴턴 물리학에서는 일정한 상대 거리를 유지하는 관찰자가 동일한 가속도를 공유해야 하기 때문에 이것이 놀랍게 보일 수 있다. 그러나 상대론적 물리학에서 우리는 어떤 외부 힘에 의해 가속되는 막대의 후행 끝점(대칭축과 평행)은 선행 끝점보다 약간 더 강하게 가속되어야 하며 그렇지 않으면 결국 끊어져야 한다는 것을 알 수 있다. 이것은 로렌츠 수축의 발현이다. 막대가 가속하면 속도가 빨라지고 길이가 줄어든다. 점점 짧아지기 때문에 뒷부분은 앞쪽보다 더 세게 가속해야 한다. 그것을 살펴보는 또 다른 방법은 뒷부분이 더 짧은 시간 내에 동일한 속도 변화를 달성해야 한다는 것이다. 이는 어느 정도 거리에서는 후행 끝의 가속도가 분산되어 린들러 지평선이 발생한다는 것을 보여주는 미분 방정식으로 이어진다.

이런 현상은 잘 알려진 '파라독스'의 근간인 벨의 우주선 역설이다. 그러나 그것은 상대론적 운동학의 단순한 결과물이다. 이것을 볼 수 있는 한 가지 방법은 가속 벡터의 크기가 해당 세계 라인의 경로 곡률에 불과하다는 것을 관찰하는 것이다. 그러나 우리 린들러 관찰자들의 세계선은 유클리드 비행기에 있는 동심원 계열의 아날로그이기 때문에 우리는 스피드 스케이트 선수들에게 익숙한 사실의 로렌츠 계열의 아날로그를 다루고 있을 뿐이다: 동심원 계열에서는 내부 원은 바깥쪽 원보다 더 빨리 구부러져야 한다(단위 호 길이당).

민코프스키 관찰자

자연스러운 선택에 의해 민코프스키 차트에 주어지는 대안 프레임도 도입할 가치가 있다.

${\displaystyle {\vec{f}_{0}=\partial _{T}\\\\vec {f}{1}}=\partial _{X}}\\\\vec{f}}}}\partial _{NY}\vec {f}}=\partial _{Z}}}}}$

위에 주어진 좌표 변환을 사용하여 이러한 벡터 필드를 변환하면 Rindler 관리도(Rinder 쐐기)에서 이 프레임이

${\displaystyle {\begin{aligned}{\vec {f}}_{0}&={\frac {1}{x}}\cosh(t)\,\partial _{t}-\sinh(t)\,\partial _{x}\\{\vec {f}}_{1}&=-{\frac {1}{x}}\sinh(t)\,\partial _{t}+\cosh(t)\,\partial _{x}\\{\vec {f}}_{2}&=\partial _{y},\;{\vec {f}}_{3}=\partial _{z}\end{aligned}}}$

타임라이크 단위 $벡터{\displaystyle {\stackrel{}{}}_{}}$ 필드 ${\displaystyle f_{\mathrm{}}}$→ 0$${\$displaystyle {\vec{f}_{$0$\}\}\}$에 의해 정의된 타임라이크 일치성의 키네마틱 분해를 계산해 보면, 확장성과 vorticity가 다시 사라지고, 가속 벡터 ${\displaystyle {vanf{\stackrel{}{}}_{}}_{}}$→ ${\displaystyle {0_{\mathrm{}}}_{}}$ ${\displaystyle {{}_{}}_{}{\stackrel{}{}}_{}}$→ ${\displaystyle 0{}_{}}$= 0 = ${\displaystyle \nabla_{\vec {f$}$}}}{0}}{\vec{f}_{0}=0}$. 즉, 이것은 지오데틱 조합이다; 상응하는 관찰자들은 관성 운동 상태에 있다. 원래 카르테시안 차트에서는 민코프스키 관찰자라고 부를 이 관찰자들은 쉬고 있다.

린들러 차트에서, 민코스키 관찰자의 월드 라인은 $좌표면{\displaystyle \mathrm{x}}$ = 0 ${\displaystyle$ x$=0}$에 대해 쌍곡선 세컨트 곡선으로 나타난다$.$ 특히 린들러 좌표에서, 이벤트 $t{\displaystyle }$= ${\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\displaystyle x}$ =${\displaystyle }$x ${\displaystyle {0\mathrm{}}_{}}$ y${\displaystyle }$= ${\displaystyle z{}_{}}$ ${\displaystyle {}_{}}$= ${\displaystyle 0_{}}$을 통과하는 $민코스키$ 관찰자의 월드 라인은 0$.$$le$ t$=t_{0},\;x=x_{0},\;y=y_{0},\;z=z_{0}}$은(는)

${\displaystyle {\begin{aligned}t&=\operatorname {artanh} \left({\frac {s}{x_{0}}}\right),\;-x_{0}<s<x_{0}\\x&={\sqrt {x_{0}^{2}-s^{2}}},\;-x_{0}<s<x_{0}\\y&=y_{0}\\z&=z_{0}\end{aligned}}}$

여기서 $s{\displaystyle }$ ${\displaystyle s}$는 이 민코스키 관찰자의 적절한 시간이다. 그의 역사 중 극히 일부만이 린들러 차트에서 다룬다는 점에 유의한다. 이것은 Rindler 차트가 지리학적으로 완전하지 않은 이유를 분명히 보여준다; 시간별 지오데믹은 차트에서 다루는 영역 밖에서 유한한 적절한 시간에 실행된다. 물론, 우리는 Rindler 차트가 지리학적으로 완성될 수 없다는 것을 이미 알고 있었다. 왜냐하면 그것은 지리학적으로 완성된 원래 카르테시안 차트의 일부분만을 다루기 때문이다.

그림에 표시된 경우, ${\displaystyle \mathrm{x}}$ ${\displaystyle {0\mathrm{}}_{}}$= 1 ${\displaystyle x_{0}=1}$및 $우리$는 s drawn${\displaystyle }${${\displaystyle }$- 1 ${\displaystyle \frac{2}{}}$,${\displaystyle }$0${\displaystyle ,}$ ${\displaystyle 1\mathrm{}}$ ${\displaystyle \frac{2}{}}$ ${\displaystyle \}}$ ${\$ {1$}{1$}{$1},\;0,\;{frac {1}{$1}{1}:{$2}}: 우측$에 라이트 콘을 그렸다.

린들러 지평선

린들러 좌표 차트는 x = 0에 좌표 특이점을 가지며, 여기서 미터법 텐서(린들러 좌표에 표시)는 소멸 결정 인자를 갖는다. 이는 x → 0으로 린들러 관찰자의 가속도가 분산되기 때문에 발생한다. 우리가 린들러 쐐기를 나타낸 그림에서 볼 수 있듯이, 린들러 차트의 로커스² x = 0은 두 개의 null 하프플레인으로 구성된 데카르트 차트의 로커스 T = X², X > 0에 해당하며 각각 null 지오데틱 합성에 의해 지배된다.

현재로서는 린들러 지평선을 린들러 좌표의 경계로 생각할 뿐이다. 우리가 린들러 좌표에서 일정한 위치를 갖는 가속 관측자 집합을 고려한다면, 그들 중 어느 누구도 T x X를 가진 사건으로부터 광 신호를 수신할 수 없다(도표에서, 이것들은 위쪽 빨간색 지평선이 있는 선 T = X의 위나 왼쪽에 있는 사건일 것이다; 그러나 이러한 관측자들은 T를 가진 사건으로부터 신호를 수신할 수 있다. ≥ X 만약 그들이 가속을 멈추고 스스로 이 선을 넘었다면) T ≤ -X (T = -X 선 왼쪽에 있는 사건들은 낮은 적색 지평선이 있고, 그러한 사건들은 그들의 과거 세계 선의 모든 미래 빛 원뿔 밖에 있다.)에 신호를 보낼 수 없었을 것이다. 또한, 우리가 이러한 가속도 관측자 집합의 구성원을 수평선에 점점 더 가깝게 생각한다면, 수평선까지의 거리가 0에 가까워질 때, 이 거리에서 관측자가 경험하는 일정한 적절한 가속도(또한 그러한 관측자가 경험하는 G-힘이 될 것이다)는 무한에 근접하게 될 것이다. 만약 우리가 블랙홀의 사건 지평선 바깥에 맴도는 일련의 관찰자들을 고려한다면, 각 관찰자들은 슈바르츠실트 좌표에서 일정한 반경을 맴돌고 있을 것이다. 실제로 블랙홀의 가까운 이웃에서는 사건 지평선에 가까운 기하학적 구조를 린들러 좌표로 설명할 수 있다. 가속 프레임의 경우 호킹 방사선을 운루(Unruh) 방사선이라고 한다. 그 연결은 가속과 중력의 동등함이다.

지리학

린들러 차트의 측지 방정식은 측지 라그랑지안으로부터 쉽게 얻을 수 있다.

${\ddtyle{\ddot{t}}+{\frac {2}{x}\,{\dot{t}=0,\\\dot{t}}^{2}=0,\\\dot{y}=0,\ddot{}}}}=0, {\ddot {}}}=0}$

물론 원래의 카르테시안 차트에서는 지오데틱스가 직선으로 나타나기 때문에 우리의 좌표 변환을 이용하여 린들러 차트에서 쉽게 얻을 수 있었다. 단, 원본 차트와는 독립적으로 입수하여 연구하는 것이 유익하며, 이 절에서 그렇게 할 것이다.

첫 번째, 세 번째, 네 번째로부터 우리는 즉시 첫 번째 통합을 얻는다.

${\dot스타일 {\dot{t}}={\frac {E}{x^{2}}},\;{\dot{y}}=P,\;\;{\dot {z}=Q}$

But from the line element we have ${\displaystyle \varepsilon =-x^{2}\,{\dot {t}}^{2}+{\dot {x}}^{2}+{\dot {y}}^{2}+{\dot {z}}^{2}}$ where ${\displaystyle \varepsilon \in \left\{-1,\,0,\,1\right\}}$ for timelike, null, and spac각각 Elike 지오다이오드(geography. 이것은 네 번째 첫 번째 적분, 즉

${\displaystyle {\stackrel{}{x}}^{}}$˙ ${\displaystyle 2^{\mathrm{}}}$= (${\displaystyle \epsilon }$+ E ${\displaystyle \frac{{2\mathrm{}}^{}}{}}$ ${\displaystyle \frac{{}^{}}{{}^{}}}$ ${\displaystyle \frac{{2\mathrm{}}^{}}{}}$)${\displaystyle }$- ${\displaystyle {P\mathrm{}}^{}}$ ${\displaystyle {}^{}}$- ${\displaystyle {Q\mathrm{}}^{}}$ ${\$}^{2$}=\좌측(\$varepsilon $+{\frac${E$^{2}}:{x^{2}}}\오른쪽)-P^{2}-Q^{2$

이것은 지오데틱 방정식의 완전한 해답을 주기에 충분하다.

nullgeodesics의 E2x2− P2−의 경우 조금 E{E\displaystyle}과 Q2{\displaystyle{\frac{E^{2}}{x^{2}}}\,-\,P^{2}\,-\,Q^{2}}, 우리는 간격 0<>은 x좌표 범위^<>EP2+Q2{0\,<, \,x\,<, \,{\frac{E\displaystyle}{\sqrt{P^{2를 참조하십시오.}\,+\,Q^{2}}$}}}$.

린들러 쐐기의 모든 이벤트를 통해 null 지오데틱을 제공하는 완전한 7개 매개변수 패밀리는 다음과 같다.

${\displaystyle {\begin{aligned}t-t_{0}&=\operatorname {artanh} \left({\frac {1}{E}}\left[s\left(P^{2}+Q^{2}\right)-{\sqrt {E^{2}-\left(P^{2}+Q^{2}\right)x_{0}^{2}}}\right]\right)+\\&\qquad \operatorname {artanh} \left({\frac {1}{E}}{\sqrt {E^{2}-(P^{2}+Q^{2})x_{0}^{2}}}\right)\\x&={\sqrt {x_{0}^{2}+2s{\sqrt {E^{2}-(P^{2}+Q^{2})x_{0}^{2}}}-s^{2}(P^{2}+Q^{2})}}\\y-y_{0}&=Ps;\;\;z-z_{0}=Qs\end{aligned}}}$

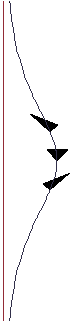
$특정{\displaystyle }$ 이벤트(즉, 하이퍼라이스 t${\displaystyle }$= 0 ${\displaysty t=0})$를 통해 일부 대표적인 null 지오데틱의 트랙을 플롯하면서,$$ 우리는 한 지점을 통해 모든 반원형의 패밀리와 직교하는 것처럼 의심스럽게 보이는 그림을 얻었다(그림 참조).^[27]

페르마 미터법

린들러 도표에서, 린들러 관찰자들을 위한 어떤 공간적 과대망상에 대한 null 지오디컬의 투영들이 단순히 반원형 호들이라는 사실은 방금 주어진 일반적인 해결책으로부터 직접 검증될 수 있지만, 이것을 볼 수 있는 아주 간단한 방법이 있다. 정적 스페이스타임은 vorticity-free timeke Killing 벡터 필드를 찾을 수 있는 시간이다. 이 경우, 우리는 (관성 관찰자가 될 필요가 없는) 해당 정적 관찰자와 직교하는 (식별적인) 공간적 과급자들로 이루어진 독특하게 정의된 집단을 가지고 있다. 이를 통해 우리는 스페이스타임에서 상속된 원래 메트릭과 일치하게 관련된 이러한 하이퍼릭스에 대한 새로운 메트릭을 정의할 수 있지만, 새로운 메트릭스(이것은 리만 3매니폴드에 있는 리만 3매니폴드에 있는 리만 3매니폴드에 대한 리만 측지학 측정기준)가 정확하게 스페이스타임의 null 지질학 예측값인 속성을 정의할 수 있다. 이 새로운 측정 지표를 Fermat 미터법이라고 하며, 정적 시간에는 선 요소가 형태를 갖는 좌표 차트가 부여된다.

${\displaystyle ds^{2}=g_{00}\,dt^{2}+g_{jk}\,dx^{j}\,dx^{j}\,dx^{k},\;j,\;k\in \{1,2,3\}}}}}$

$t{\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle t=0}$의 페르마트 메트릭은 단순하다$$.

${\displaystyle d\rho ^{2}={\frac {1}{-g_{00}}}\왼쪽(g_{jk}\,dx^{j}\,dx^{k}\오른쪽)}$

(여기서 메트릭 코퍼스는 $t{\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle t=0}$에서 평가되는 것으로 이해된다.)$$

린들러 도표에서 타임라이크 번역${\displaystyle {\mathrm{}}_t}$ t$${\$displaystyle \partial _{t}$은 그런 킬링 벡터 필드이므로$$, 이것은 정적 스페이스타임(Minkowski spacetime은 물론 사소한 아인슈타인 필드 방정식의 정적 진공 솔루션이기 때문에 놀랄 일도 아니다)이다. 따라서, 우리는 즉시 린들러 관찰자들을 위해 페르마 측정지표를 작성할 수 있다.

${\displaystyle d\rho ^{2}={\frac {1}{x^{2}}}\왼쪽(dx^{2}+dy^{2}+dz^{2}\오른쪽)\;\;\;\forall x>0,\;\;\forall y,z}$

그러나 이것은 위쪽 절반 공간 차트에서 쌍곡선 3공간 H의³ 잘 알려진 선 요소다. 이는 쌍곡면 H에² 대해 잘 알려진 상반면 차트와 밀접하게 유사하며, 이는 정합성 지도 문제(더 많은 것)와 관련하여 여러 세대의 복잡한 분석 학생들에게 친숙하며, 많은 수학적으로 마음에 드는 독자들은 상반면 모델에서 H의² 지질학이 단순히 반반면이라는 것을 이미 알고 있다. (실제 축으로 표현되는 무한대의 원과 직교).

대칭

린들러 차트는 민코프스키 스페이스타임의 좌표 차트인 만큼 선형적으로 독립적인 킬링 벡터 필드 10개를 찾을 수 있을 것으로 기대하고 있다. 실제로 카르테시안 차트에서 우리는 10개의 선형 독립 킬링 벡터 필드를 쉽게 찾을 수 있으며, 각각 하나의 매개변수 부분군 시간 변환, 3개의 공간, 3개의 회전 및 3개의 부스트를 생성할 수 있다. 이 두 그룹이 함께 민코프스키 스페이스타임의 대칭 그룹인 (적절한 등시성) 푸앵카레 그룹을 생성한다.

다만 킬링벡터 방정식을 직접 적어서 푸는 것이 교훈적이다. 우리는 네 개의 친숙해 보이는 킬링 벡터 필드를 얻었다.

${\displaystyle \property_{t}\;\;\put_{y}\\;\\put_{z}\put_{y}+y\,\put_{z}}$

(시간 번역, 가속도 방향에 직교하는 공간 번역, 가속도 방향에 직교하는 공간 회전) + 6개 더하기:

${\displaystyle {\regated}&\exp(\pm t)\,\left\frac {y}}\cHB\pm\{t}\pm\pm\eft[y\,\ft_{x}-x\,\ft_{y}\right]\right)\\&\exp(\pm t)\,\left\frac {z}{x}\,\pm_{t}\pm\pm\left[z\,\pm_{x}-x\,\pm_{z}\right]\right)\\&\exp(\pm t)\,\left\frac {1}{x}\,\filename _{t}pm \pm \pm \pm \{x}\right)\end{aigned}}}}}}$

(부호를 일관되게 + 또는 -로 선택하는 경우). 우리는 이것들이 표준 발전기와 어떻게 관련되는지 알아내기 위한 연습으로 남겨두었다; 여기서 우리는 ${\displaystyle {카트리지안}_{}}$ 차트에서$$ $\partial {\displaystyle {\mathrm{}}_{}}$ T ${\$에 해당하는 발전기를 얻을 수 있어야 한다는 것을 지적하고 싶다. 그러나 Rindler 쐐기는 분명히 이 번역에서 불변하는 것은 아니다. 어떻게 이럴 수가 있지? 해답은 부드러운 다지관의 부분 미분 방정식 시스템에 의해 정의되는 어떤 것과 마찬가지로 킬링 방정식은 일반적으로 국소적으로 정의된 해결책을 가지고 있지만, 그것들은 세계적으로 존재하지 않을 수 있다는 것이다. 즉, 그룹 파라미터에 대한 적절한 제한으로 킬링 플로우는 항상 적절한 지역적 인접 지역에서 정의될 수 있지만, 흐름은 세계적으로 잘 정의되지 않을 수 있다. 이것은 로렌츠 다지관의 연구에서도 같은 문제가 발생하기 때문에 로렌츠 다지관의 per se와 아무런 상관이 없다.

거리 개념

린들러 차트의 연구에서 배워야 할 많은 귀중한 교훈들 중 하나는 사실 린들러 관찰자들이 사용할 수 있는 거리에 대한 몇 가지 뚜렷한 개념들이 있다는 것이다.

첫째는 우리가 위에서 암묵적으로 고용한 것이다: 공간 과소평가 $t{\displaystyle }$= ${\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$에 유도된 리만 측량$.$ 우리는 이것을 이 유도된 리만 측정법에 해당하기 때문에 자 거리라고 부를 것이지만, 그것의 작동 의미는 즉시 분명하지 않을 수도 있다.

물리적 측정의 관점에서, 두 세계선 사이의 거리에 대한 보다 자연스러운 개념은 레이더 거리다. 이것은 우리의 관찰자의 세계선(사건 A)에서 어떤 작은 물체의 세계선(사건 B)으로 null 지오데틱을 보내서, 그 위에 그것이 반영되고(사건 B) 관찰자에게 되돌아오는(사건 C)로 계산한다. 레이더 거리는 관찰자가 운반하는 이상적인 시계에 의해 측정된 왕복 이동 시간을 나누어 얻는다.

(Minkowski spacetime, 다행히도 우리는 두 세계선 사이에 복수의 null 지오데틱 경로의 가능성을 무시할 수 있지만, 우주론 모델이나 다른 어플리케이션에서는^[which?] 사물이 그렇게 간단하지 않다. 또한 우리는 두 관찰자 사이의 거리에 대한 이러한 개념이 관찰자를 서로 바꿀 때 대칭적인 개념을 제공한다고 가정하지 않도록 주의해야 한다.)

In particular, consider a pair of Rindler observers with coordinates ${\displaystyle x=x_{0},\;y=0,\;z=0}$ and ${\displaystyle x=x_{0}+h,\;y=0,\;z=0}$ respectively. (Note that the first of these, the trailing observer, is accelerating a bit harder, in order to keep up with (주요 관찰자) 린들러 선 $요소$에서 ${\displaystyle d}$y = ${\displaystyle d\mathrm{z}}$ = 0 ${\displaystyle dy=dz=0}$을(를) 설정하면 가속 방향으로 움직이는 null 지오데틱스의 방정식을 쉽게 얻을 수 있다.

${\displaystyle t-t_{0}=\log \lefted\frac {x}{x_{0}}\오른쪽)}$

따라서 이 두 관측자 사이의 레이더 거리는 다음과 같다.

${\displaystyle x_{0}\,\log \좌측(1+{\frac {h}{x_{0}}\우측)=h-{\frac {h^{2}{2\,x_{0}}}+O\왼쪽(h^{3}\오른쪽)}$

이것은 눈금자 거리보다 약간 작지만, 근처의 관찰자들은 그 불일치를 무시할 수 있다.

세 번째 가능한 거리의 개념은 다음과 같다: 우리의 관찰자는 어떤 물체(점 물체가 아닌)에 놓여진 단위 원반으로 하위 각도를 측정한다. 그의 위치에서 나타나는 각도. 우리는 이것을 광직경 거리라고 부른다. 밍코프스키 스페이스타임의 null 지오데틱스라는 단순한 특성 때문에, 우리 쌍의 린들러 관찰자 사이의 광학적 거리(가속 방향과 정렬)를 쉽게 판단할 수 있다. 스케치에서 광 직경 거리는 $h$+ 1 $\frac{{x\mathrm{}}_{}}{}$ $\frac{{}_{}}{}$+ O ($h$ ${3\mathrm{}}^{}$ )${\$ h$+{\frac${1$}{x_{0}}}+$와 같이 스케일링할 수 있어야 한다.$O\왼쪽(h^{3}\오른쪽)}$. 따라서 선도 관찰자(사례 > (\displaystyle $h>0})$까지의 거리를 추정하는 후행 관찰자의 경우 광학적 거리는 눈금자 거리보다 약간 커 레이더 거리보다 약간 크다. 이제 독자는 후행 관찰자에 대한 거리를 추정하는 선도 관찰자의 경우를 잠시 고려해야 한다.

거리에 대한 다른 개념들도 있지만, 요점은 명확하다. 이러한 다양한 개념의 값들은 주어진 한 쌍의 린들러 관찰자들에 대해 일반적으로 일치하지 않지만, 그들은 모든 한 쌍의 린들러 관찰자들이 일정한 거리를 유지한다는 것에 모두 동의한다. 매우 가까운 린들러 관찰자들이 상호 정지되어 있다는 사실은 위에서 언급했듯이 린들러 응축의 팽창 텐서가 동일하게 소멸된다는 사실에서 비롯된다. 그러나, 우리는 여기서 다양한 의미에서 이 경성 성질이 더 큰 규모로 유지된다는 것을 보여 주었다. 상대론적 물리학에서 어떤 로드도 경직되게 가속할 수 없으며(그리고 어떤 디스크도 경직되게 회전할 수 없다는) 적어도 비균형적인 스트레스를 지속하지 않고는 그렇지 않다는 잘 알려진 사실을 고려할 때, 이것은 실로 주목할 만한 경직성 속성이다. 이것을 가장 쉽게 볼 수 있는 방법은 뉴턴 물리학에서 단단한 몸을 '차다'면 체내의 모든 물질의 원소가 즉시 운동 상태를 변화시킬 것이라는 것을 관찰하는 것이다. 이는 물론 물리적 영향을 미치는 어떤 정보도 빛의 속도보다 빨리 전송될 수 없다는 상대론적 원리와 양립할 수 없다.

그것은 막대가 그 길이를 따라 어느 곳에 가해지는 어떤 외부 힘에 의해 가속되는 경우, 막대의 다양한 위치에 있는 물질의 원소는 막대가 묶이지 않고 연장되지 않고 궁극적으로 끊어지지 않는다면 모두 동일한 가속도의 크기를 느낄 수 없다는 것을 따른다. 다시 말해, 파손되지 않는 가속 막대는 그 길이에 따라 달라지는 스트레스를 견뎌야 한다. 더욱이 우리가 어떤 물체를 "차려"든, 혹은 점차적으로 가속하려고 하든 시간이 다른 힘을 가진 어떤 사고 실험에서 우리는 상대론적 운동학과는 일치하지 않는 기계적 모델을 피하는 문제를 피할 수 없다(신체의 먼 부분들은 가해진 힘에 너무 빨리 반응하기 때문이다).

통치자 거리의 운영상의 중요성에 대한 문제로 돌아가서, 우리는 이것이 우리의 관찰자들이 아주 천천히 손에서 손으로 지나갈 때 얻을 수 있는 거리여야 하며, 이 작은 통치자는 끝에서 끝까지 반복적으로 정해져 있다. 그러나 이러한 해석을 구체적으로 정당화하려면 어떤 종류의 재료 모델이 필요할 것이다.

곡선 스페이스타임에 대한 일반화

위에서 설명한 린들러 좌표는 페르미 정상 좌표로서 곡선 스페이스타임으로 일반화할 수 있다. 일반화에는 적절한 정사각형 테트라드를 구성한 다음 페르미-워커 운송 규칙을 사용하여 주어진 궤적을 따라 운송하는 것이 필수적이다. 자세한 내용은 아래 참조에서 Ni와 Zimmermann의 논문을 참조하십시오. 그러한 일반화는 실제로 지구에 기반을 둔 실험실에서 관성 효과와 중력 효과를 연구할 수 있을 뿐만 아니라, 더 흥미로운 결합 관성-중력 효과를 연구할 수 있게 해준다.

역사

개요

코틀러-몰러 및 린들러 좌표

알버트 아인슈타인(1907)은 ^{[H 13]}등가속도 프레임 내에서 효과를 연구하여 (2c에 상당하는 빛의 속도 및 좌표 의존 시간 확장에 대한 방정식을 얻었으며, 관측자의 기원과 독립적인 공식을 만들기 위해 레이더 좌표와 형식적으로 합의하여 시간 팽창(2i)을 얻었다. Born 강직성 개념을 소개하면서 Max Born(1909)은 ^{[H 14]}쌍곡 운동 공식은 (2d)에 상당하는 "초강력 가속 참조 시스템"(독일어: hyperbolisch beschleunigtes Bezugsystem)으로의 변환으로 사용될 수 있다고 언급했다. 보른의 작품은 아놀드 소머펠트(1910)^{[H 15]}와 막스 폰 라우에(1911)^{[H 16]} 둘 다 가상의 숫자를 사용하여 얻은(2d)에 의해 더욱 정교하게 설명되었는데, 좌표(2d) 이외에 가상의 숫자로 미터법(2e)도 얻은 볼프강 파울리(1921)^[16]가 요약하였다. 아인슈타인(1912년)^{[H 17]}은 정적 중력장을 연구하여 코틀러-뮐러 메트릭(2b)과 빛의 좌표 의존 속도를 이용하여 공식(2a)에 대한 근사치를 얻었다.^[28] 헨드릭 로렌츠(1913)^{[H 18]}는 아인슈타인의 동등성 원리와 균일한 중력장을 연구하면서 (2d, 2e, 2f)와 유사한 좌표를 얻었다.

상세한 설명은 해당 정사각형 테트라드, 변환 공식, 미터법(2a, 2b)을 공식화한 프리드리히 코틀러(1914년)^{[H 19]}가 했다. 또한 Karl Bollert(1922)^{[H 20]}는 균일한 가속도와 균일한 중력장에 대한 연구에서 미터법(2b)을 얻었다. Born 강직성과 관련된 논문에서 Georges Lemaître(1924년)^{[H 21]}는 좌표와 미터법(2a, 2b)을 얻었다. 알버트 아인슈타인과 네이선 로젠(1935년)은 (2d, 2e)을 동질적인 중력장에 대한 "잘 알려진" 표현으로 묘사했다.^{[H 22]} 크리스티안 뮐러(1943)가 ^{[H 11]}동종 중력장과 관련된 연구로 (2a, 2b)를 얻은 후, 미스너&^{[H 23]}소른&휠러(1973)^[2]는 같은 방정식을 얻기 위해 페르미-워커 수송을 이용했다.

이러한 조사가 평탄한 시간대와 관련된 반면, 볼프강 린들러(1960)^[14]는 곡선 시간대의 쌍곡 운동을 분석하여 (1966) 평탄한 시간대의 쌍곡좌표(2d, 2e)와 슈바르츠실트 공간의 크러스칼 좌표 사이의 유사성을 보여주었다.^[15] 이는 관찰자가 쌍곡선 운동으로 측정한 언루 방사선의 공식화에 후속 작가들에게 영향을 미쳤는데, 이는 블랙홀의 호킹 방사선에 대한 설명과 유사하다.

지평선

태어난(1909년)은 출생 강체 쌍곡선 운동의 내부 점은 지역 X에서 될 수 있다는 것을/(X2− T2)>0{\displaystyle X(X^{2}-T^{2}\right)>0}.[H24]조머 펠트(1910년)은 좌표 관성과 과장된 좌표 간 변환하는데 허용되 T<>X{\di을 충족해야 하며 정의했다.$splaystyle T<X}$.^{[H 25]} Kottler (1914)^{[H 26]} defined this region as ${\displaystyle X^{2}-T^{2}>0}$, and pointed out the existence of a "border plane" (German: Grenzebene) ${\displaystyle c^{2}/\alpha +x}$, beyond which no signal can reach the observer in hyperbolic motion. 이를 '관찰자의 수평선'(독일어: 볼러트(1922년)의 호라이즌트 데 보바흐터).^{[H 27]} 린들러(1966)는 크러스칼 좌표에서 그러한 지평선과 지평선 사이의 관계를 증명했다.^[15]

레이더 좌표

Stjephan Mohorovichichi(1922년)^{[H 28]}는 볼러트의 형식주의를 이용하여 일부 파라미터에 대해 다른 선택을 하였고, 다른 인쇄 오류와 함께 볼러트(1922b)가 정정하는 미터법(2h)을 얻어 모호로비치치치치(1923년)가 인쇄 오류 없는 버전을 주도록 하였다. 또, 모호로비치치는 미터법(2b, 현재 코틀러-모울러 미터법으로 불리고 있음)이 틀렸다고 잘못 주장했는데, 이것은 볼러트(1922년)에 의해 반박되었다.^{[H 29]} 미터법(2h)은 해리 래스(1963)에 의해 재발견되었는데,^[13] 해리 래스(1963)는 때로 "래스 좌표"라고 불리는 해당 좌표(2g)를 주기도 했다.^[9] 미터법(2h)은 물론 (2a, 2b)도 프리츠 로흘리치(1963년)에 의해 도출되었다.^[12] 결국 라스 좌표(2g, 2h)는 데스로게 & 필포트(1987년)에 의해 레이더 좌표로 식별되었다.^[29][8]

과거 공식이 있는 표

아인슈타인 ([H 30]1907) ${\displaystyle {\scriptstyle {\cfrac}\tau \좌측(1+{\frac {\fract \xi }{c^{2}}}\우측)\\\c^ma =\tau e^{\c^{2}}\\c\left(1+{\frac{\xi \}{c^{2}}}\right)\end{c}}}}}}}}{c^}}}}}}}}}{pau{nd}}}}}}}}}}}}}}}}}}}}$ 출생(1909)[H 14] ${\displaystyle {\scriptstyle {\begin{matrix}x=-q\xi ,\ y=\eta ,\ z=\zeta ,\ t={\frac {p}{c^{2}}}\xi \\\left(p=x_{\tau },\ q=-t_{\tau }={\sqrt {1+p^{2}/c^{2}}}\right)\\\downsymbol {\downarrow }\\x^{2}-c^{2}=\xi ^{2}\i ^{2}\end}}}}}}}}}}}}$ 헤르글로츠 (1909)[H 31][30] ${\displaystyle {\scriptstyle {\begin{matrix}{\begin{aligned}x&=x'\\y&=y'\\t-z&=(t'-z')e^{\vartheta }\\t+z&=(t'+z')e^{-\vartheta }\end{aligned}}\\{\boldsymbol {\downarrow }}\\x=x_{0},\quad y=y_{0},\quad z={\sqrt {z_{0}^{2}+t^{2}}}\끝{{matrix}}}}}}$ 소머펠트(1910)[H 15] ${\displaystyle \script style {\signed}x&=r\cos \varphi \\y&=y'\z&=l>r\sin \varphi \=i\l=ict\end}}}}}$ 폰 라우에 (1911년)[H 32] ${\displaystyle \begin{aigned}X&=R\cos \varphi \\\L&=R\sin \varphi \\\\2}+R^{2}+L^{2}\tanvarphi &={X}}}}}}}}\\frac {X}\end{aigned}}}}}}}}}}}}}}}}}}}}}}}}정렬}$ 아인슈타인 (1912년)[H 17] ${\displaystyle {\scriptstyle {\begin{matrix}d\xi ^{2}-d\tau ^{2}=dx^{2}-c^{2}dt^{2}\\{\boldsymbol {\downarrow }}\\c=c_{0}+ax\\{\boldsymbol {\downarrow }}\\{\begin{aligned}\xi &=x+{\frac {ac}{2}}t^{2}\\\eta &=y\\\zeta &=z\\\tau &=ct\end{aligned}}\end{matrix}}}}$ 코틀러(1912년)[H 33] ${\displaystyle {\scriptstyle {\cripty}x^{1}&=x_{0}^{1}}\x^{0}^{{0}}}}}}\x^{3}\cos i\varphi \x^{}}}=bsin ivarphi \}}}{{}}}}}}}}}}}}}}}}}}}}}}}}}}}정렬했다.$ 로렌츠(1913년)[H 18] ${\displaystyle {\scriptstyle {\c}dc={g}{c}dz\\\hline {\line}\\line {\j'-z_{0}^{primate }}\ct&=b\lift(z-z_{0}^{0}{0}^}\primprimprimprimprimprimprimeprimprimeprimeprimeprimeprimeprimeprim)\\a&, ={\frac{1}{2}}\left(e^{kt의}+e^{-kt}\right)\\b&, ={\frac{1}{2}}\left(e^{kt의}-e^{-kt}\right)\end{정렬}}\\{\boldsymbol{\downarrow}}\\c'=k\left(z'-z_{0}일 경우 ^{}\prime \right),\ z'-z_{0}^{\prime}={\frac{{2c^}}{g}}\\{\boldsymbol{\downarrow}}\\{\begin{정렬}&, dx^{2}+dy^{2}+dz^{2}-c^{2}dt\\&, =dx^{\prime 2}+dy^{\prime 2}+dz^{\prime 2.}-c^{\prime 2}dt^{\premise 2}\ended}\edged}\end{data}}}}$

코틀러(1914a)[H 34] ${\displaystyle{\scriptstyle{\begin{행렬}{\begin{정렬}x^{(1)}&.=x_{0}^{(1)}\\x^{(2)}&.=x_{0}^{(2)}\\x^{(3)}&, =b\cos iu\\x^{(4)}&, =b\sin iu\end{정렬}}\\{\boldsymbol{\downarrow}}\\ds^{2}=-c^{2}d\tau ^ᆸ=b^ᆹ(()^{2}\\{\boldsymbol{\downarrow}}\\{\begin{행렬}c_{1}^{(1)}=0,&, &, c_{1}^{(2)}=0,&, &, c_{1}^{(3)}=-\sin iu,&, &, c_{1}^{(4)}=\cos iu,\\c_{2}.^{(1)}=0,&&c_{2}^{(2)}=0,&&c_{2}^{(3)}=-\cos iu,&&c_{2}^{(4)}=-\sin iu,\end{matrix}}\\{\boldsymbol {\downarrow }}\\dS^{2}=(dX')^{2}+(dY')^{2}+(dZ')^{2}-\left(c+{\frac {Z'c}{b}}\right)^{2}dT'\\{\boldsymbol {\downarrow }}\\c'=c+{\frac {Z'c^{2}}{b}}\cdot {\frac {1}{c}}\end{matrix}}}}$ 코틀러(1914b)[H 35] ${\displaystyle \scriptstyle{\begin{행렬}{\begin{행렬}c_{1}^{ᆨ}=0,&, &, c_{1}^{ᆩ}=0,&,&c_{1}^{ᆪ}={\frac{1}{나는}}\sinh u,&, &, c_{1}^{ᆫ}=\cosh u,\\c_{2}^{ᆬ}=0,&, &, c_{2}^{ᆭ}=0,&,&c_{2}^{ᆮ}={\frac{1}{나는}}\cosh u,&,&c_{2}^{ᆯ}=-\sinh u,\\c_{3}^{ᆰ}=1,&, &, c_{3}^{ᆱ}=0,&,&c_{3}^{ᆲ}=0,&.앰프,&c_{3}^{(4)}=0,\\c_{4}^{(1)}=0,&, &, c_{4}^{(2)}=1,&, &, c_{4}^{(3)}=0,&.&c_{4}^{(4)}=0,\end{matrix}}\\{\boldsymbol {\downarrow }}\\X=x+\Delta ^{(2)}c_{2}+\Delta ^{(3)}c_{3}+\Delta ^{(4)}c_{4}\\{\boldsymbol {\downarrow }}\\{\begin{aligned}X&=x_{0}+{\mathfrak {X}}'\\Y&=y_{0}+{\mathfrak {Y}}'\\Z&=\left(b+{\mathfrak {Z}}'\right)\cosh {\mathfrak {u}}\\cT&=\left(b+{\mathfrak {Z}}'\right)\sinh {\mathfrak {u}}\end{aligned}}\\\left(\Delta ^{(2)}={\mathfrak {X}}',\ \Delta ^{(3)}={\mathfrak {Y}}',\ \Delta ^{(4)}={\mathfrak {Z}}'\right)\\\boldsymbol {\downarrow }\\\begin{aigned}{\mathfrak {X}&=X_-x_{0}+q_{x}}T\\{\mathfrak{Y}'&=Y_{0}-y_{0}+q_{y}}T\\b+{\mathfrak {Z}&={\sqrt {\\sqrt}\\좌측(Z_{0}+q_{x})T\right)^{2}-c^{2}T^{2}}}\\c{\mathfrak {T}&=b\operatorname {artanh} {\frac {cT}{Z_{0}+q_{x}}T}}\end{aigned}\\왼쪽(X=X_{0}+q_{x}T,\ Y=Y_{0}+q_{y}T,\ Z=Z_{0}+q_{x}T\오른쪽)\\{\boldsymbol {\downarrow }}\\dS^{2}=(d{\mathfrak {X}}')^{2}+(d{\mathfrak {Y}}')^{2}+(d{\mathfrak {Z}}')^{2}-c^{2}\left({\frac {b+{\mathfrak {Z}}'}{b^{2}}}\right)^{2}(d{\mathfrak {T}}')^{2}\end{matrix}}}$ 코틀러 (1916, 1918)[H 36] ${\displaystyle \scriptstyle{\begin{행렬}{\begin{정렬}x&, =x'\\y&, =y'\\{\frac{{2c^}}{\gamma}}+z&, =\left({\frac{{2}}{\gamma}}+z'\right c^)\cosh{\frac{\gamma the의 생략}{c}}\\ct&, =\left({\frac{{2}}{\gamma}}+z'\right c^)\sinh{\frac{\gamma the의 생략}{c}}\end{정렬}}\\{\boldsymbol{\downarrow}}\\ds^{2}=dx^{\prime 2}+dy^{\prime 2}+dz^{\prime. 2}-\left(c+{\frac {\c}{c}z'\right){}^{2}dt^{\premy 2}\end{data}}}$

파울리 (1921년)[H 37] ${\displaystyle \scriptstyle{\begin{행렬}{\begin{정렬}x^{1}&, =\varrho\cos \varphi \\x^{4}&, =\varrho\sin \varphi \end{정렬}}\\{\boldsymbol{\downarrow}}\\ds^ᆵ=\left(d\xi ^{1}\right)^ᆶ+\left(^{2}\rightd\xi)^ᆷ+\left(d\xi ^{3}\right)^ᆸ+\left(\xi ^{1}\right)^ᆹ\left(d\xi ^{4}\right)^ᆺ\\\left(\xi ^{(1)},\ \xi ^{(2)}= =\varrho.x^{(2)},\xi ^{(3)}=x^{(3)},\\xi ^{(4)}=\varphi \right)\end}}}}$ 볼러트 (1922년)[H 20] ${\displaystyle {\scriptstyle {\begin{matrix}ds^{2}=c^{2}\left(1+{\frac {\gamma _{0}x}{c^{2}}}\right)d\tau ^{2}-dx^{2}-dy^{2}-dz^{2}\\\hline ds^{2}=g_{44}dx_{4}^{2}+g_{11}dx_{1}^{2}+g_{22}\left(dx_{2}^{2}+dx_{3}^{2}\오른쪽)\\\boldsymbol {\downarrow }\\V'-{\frac {g_{11}{11}V'=0\\\좌측(g_{22}-1,\g_{11}=-1,\{11}=1,\V'=0,\V=ax+b\우측)\\{\\downarrow }\\ds^{2}=dx_{4}}^{2}(ax+b)^{2}-dx^{2}-dy^{2}-dz^{2}\end}}}}}}$ 모호로비치(1922년, 1923년); 볼러트(1922b)[H 28] ${\displaystyle {\scriptstyle {\begin{matrix}{\text{Mohorovichich(1922):}}\\g_{11}=g_{44}=V^{2},\ VV''-V'^{2}=0,\ V\left(x_{1}\right)=e^{ax_{1}}\\{\boldsymbol {\downarrow }}\\ds^{2}=e^{2a}\left(-dx_{4}^{2}+dx_{1}^{2}\오른쪽)+dx_{2}^{2}+dx_{3}^{2}\\\\{\text{bollert(1922b):}}\\ds^{2}=e^{2ax}\왼쪽 (-dx_{4}^{2}+dx_{1}^{2}\오른쪽)+dx_{2}^{2}+dx_{3}^{2}\\\\\{\text{model}모호로비치(1923년)의 최종 수정:}}\\ds^{2}=e^{2ax_{1}\좌측dx_{4}^{2}+dx_{1}}^{2}\오른쪽)+dx_{2}^{2}+dx_{3}}^{2}\end{{11}}}}}}}$ 레마슈트레 (1924년)[H 21] ${\displaystyle {\scriptstyle {\begin{matrix}{\begin{aligned}1+g\xi =&(1+gx)\cosh gt\\g\tau =&(1+gx)\sinh gt\end{aligned}}\\{\boldsymbol {\downarrow }}\\ds^{2}=-dx^{2}-dy^{2}-dz^{2}+(1+gx)^{2}dt^{2}\end{matrix}}}}$ 아인슈타인 & 로젠 (1935년)[H 22] ${\displaystyle \scriptstyle {\begin{matrix}{\begin{aligned}\xi _{1}&=x_{1}\cosh \alpha x_{4}\\\xi _{2}&=x_{2}\\\xi _{3}&=x_{3}\\\xi _{4}&=x_{1}\sinh \alpha x_{4}\end{aligned}}\\{\boldsymbol {\downarrow }}\\ds^{2}=-dx_{1}^{2}-dx_{2}^{2}-dx_{3}^{2}+\alpha {}^{2}x_{1}^{2}dx_{4}^{2}\end{matrix}}}$ 뮐러(1952년)[H 23] ${\displaystyle \scriptstyle {\begin{matrix}\alpha _{ik}=\왼쪽({\begin{matrix}U_{4}/ic&0&iU_{1}/c\0&0&0&0&0&#&0&0&0&#\\\\\\\\\\\\\\\\\\\\\\\U_{1}/ic&0&0&0&U_{4}/ic\end{matrix}\오른쪽)\\\\U_{i}=\왼쪽(c\sinh {\frac {g\tau }{c},\0,\ig\cosh {\frac {g\tau }}{c}\오른쪽)\\{\boldsymbol {\downarrow }}\\X_{i}=\mathbf {f} _{i}(t)+x^{\prime \kappa }\alpha _{\kappa i}(\tau )\\{\boldsymbol {\downarrow }}\\{\begin{aligned}X&={\frac {c^{2}}{g}}\left(\cosh {\frac {gt}{c}}-1\right)+x\cosh {\frac {gt}{c}}\\Y&=y\\Z&=z\\T&={\frac {c}{g}}\sinh {\frac {gt}{c}}+x{\frac {\sinh {\frac {gt}{c}}}{c}}\end{aligned}}\\{\boldsymbol {\downarrow }}\\ds^{2}=dx^{2}+dy^{2}+dz^{2}-c^{2}dt^{2}\left(1+gx/c^{2}\right)^{2}\\\\\end{matrix}}}$

참고 항목

• 벨의 우주선 역설은 때때로 논란이 되는 주제를 위해 종종 린들러 좌표를 사용하여 연구했다.
• Minkowski spacetime에서 특정 가속도 관찰자의 움직임에 적응한 또 다른 중요한 좌표계를 위해 태어난 좌표.
• 일치성(일반 상대성)
• 에렌페스트 역설은 때때로 논란이 되는 주제를 위해 종종 Born 좌표를 사용하여 연구했다.
• 일반 상대성에서의 프레임 필드
• 일반 상대성 자원
• 밀네 모형
• 레이쇼우두리 방정식
• 언루 효과

참조

사료

추가 읽기

유용한 배경:

• Boothby, William M. (1986). An Introduction to Differentiable Manifolds and Riemannian Geometry. New York: Academic Press. ISBN 0-12-116052-1. 부드러운 다지관의 벡터장에 관한 배경은 4장을 참조한다.
• Frankel, Theodore (1979). Gravitational Curvature: an Introduction to Einstein's Theory. San Francisco : W. H. Freeman. ISBN 0-7167-1062-5. 페르마 메트릭의 파생은 8장을 참조한다.

린들러 좌표:

• Rindler, Wolfgang (1969). Essential Relativity. New York, Van Nostrand Reinhold Co. doi:10.1007/978-1-4757-1135-6. ISBN 978-0-387-90201-2.

• Misner, Charles; Thorne, Kip S. & Wheeler, John Archibald (1973). Gravitation. San Francisco: W. H. Freeman. ISBN 0-7167-0344-0. 섹션 6.6을 참조하십시오.
• Rindler, Wolfgang (2001). Relativity: Special, General and Cosmological. Oxford: Oxford University Press. ISBN 0-19-850836-0.
• Ni, Wei-Tou; Zimmermann, Mark (1978). "Inertial and gravitational effects in the proper reference frame of an accelerated, rotating observer". Physical Review D. 17 (6): 1473–1476. Bibcode:1978PhRvD..17.1473N. doi:10.1103/PhysRevD.17.1473.

린들러 수평선:

• Jacobson, Ted & Parenti, Renaud (2003). "Horizon Entropy". Found. Phys. 33 (2): 323–348. doi:10.1023/A:1023785123428. S2CID 16826867. 에프린트판
• Barceló, Carlos; Liberati, Stefano & Visser, Matt (2005). "Analogue Gravity". Living Reviews in Relativity. 8 (1): 12. arXiv:gr-qc/0505065. Bibcode:2005LRR.....8...12B. doi:10.12942/lrr-2005-12. PMC 5255570. PMID 28179871.