생성된 좌표

상대론 물리학에서 Born 좌표도는 특수 상대성의 평면 스페이스타임인 (의 일부) Minkowski spacetime에 대한 좌표 차트다. 흔히 랜지빈 관찰자(Langevin 관찰자)라고 불리는 상대적 속도로 단단하게 회전하는 링이나 원반에 타는 관찰자의 신체 경험을 분석하는 데 사용된다. 이 차트는 회전하는 신체의 상대론적 물리학에 관한 1909년 그의 연구 때문에 종종 맥스 본에 기인한다. 플랫 스페이스타임에서의 가속 적용에 대한 개요는 가속(특수 상대성) 및 적절한 기준 프레임(평탄한 스페이스타임)을 참조하십시오.

관성 시나리오(즉, 관성 프레임에서의 측정)에 의한 경험으로부터, 랜지빈 관찰자는 각각 표준 아인슈타인 관습이나 느린 클럭 동기화에 의해 시계를 동기화한다(두 가지 내부 동기화 모두). 어떤 랜지빈 관찰자에게 이 방법은 완벽하게 효과가 있다. 바로 인접한 시계 내에서 시계가 동기화되고 빛이 우주에서 등방성을 전파한다. 그러나 관측자들이 우주에서 닫힌 길을 따라 시계를 맞추려고 하는 경험은 어리둥절하다: 항상 다른 시간을 가진 적어도 두 개의 이웃 시계가 있다. 상황을 개선하기 위해 관찰자는 외부 동기화 절차(시간 t — 또는 링 라이딩 관찰자의 경우 고정 반지름 r에 대한 적절한 좌표 시간)에 동의한다. 이 합의에 의해, 단단하게 회전하는 디스크를 탄 랜지빈 관측자들은 그들 자신들 사이의 작은 거리를 측정한 결과 디스크의 기하학이 유클리드인이 아니라는 결론을 내릴 것이다. 어떤 방법을 사용하든, 그들은 그 기하학이 특정한 리만 메트릭스, 즉 란제빈-란다우-라이프시츠 메트릭스에 의해 충분히 근사치된다고 결론 내릴 것이다. 이는 쌍곡면의 기하학적 구조(각각 마이너스 곡선 -3Ω² 및 -3Ω² r²)에 의해 매우 근사하게 나타난다. 그러나 이러한 관찰자가 더 큰 거리를 측정하면 어떤 측정 방법을 사용하느냐에 따라 다른 결과를 얻을 것이다! 그러나 그러한 모든 경우에, 그들은 어떤 리만 측정기준과도 일치하지 않는 결과를 얻을 가능성이 가장 높다. 특히 그들이 이미 지적한 비대칭과 같은 다양한 효과 때문에 가장 단순한 거리 개념인 레이더 거리를 사용한다면, 디스크의 '지오메트리'는 비단유클리드만이 아니라 비리만적인 것이라고 결론짓게 될 것이다.

회전 디스크는 역설적이지 않다. 관찰자들은 상황을 분석하기 위해 어떤 방법을 사용하든, 결국 관성 프레임이 아닌 회전 디스크를 분석하는 그들 자신을 발견한다.

원통형 차트의 Langevin 관찰자

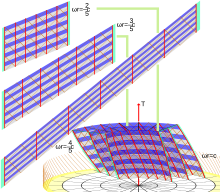
본 차트에 동기를 부여하기 위해 먼저 밍코프스키 스페이스타임에 대한 일반적인 원통형 좌표 차트로 대표되는 랜지빈 관측자 가족을 고려한다. 이러한 관찰자들의 세계선은 시시각각의 조화를 이루는데, 이는 사라져 가는 팽창 텐서라는 의미에서 경직된 것이다. 이들은 원통형 대칭 축을 중심으로 단단하게 회전하는 관찰자를 대표한다.

선 요소로부터

${\displaystyle {\begin{aligned}&\mathrm {d} s^{2}=-\mathrm {d} T^{2}+\mathrm {d} Z^{2}+\mathrm {d} R^{2}+R^{2}\,\mathrm {d} \Phi ^{2},\;\;\\&-\infty <T,\,Z<\infty ,\;0<R<\infty ,\;-\pi <\Phi <\pi \end{aligned}}}$

고정(내부) 관측자의 로컬 로렌츠 프레임을 나타내는 프레임 필드를 즉시 읽을 수 있다.

${\displaystyle {\vec {e}}_{0}=\partial _{T},\;\;{\vec {e}}_{1}=\partial _{Z},\;\;{\vec {e}}_{2}=\partial _{R},\;\;{\vec {e}}_{3}={\frac {1}{R}}\,\partial _{\피 }}$

여기서 $e{\displaystyle {\stackrel{}{}}_{}}$→ ${\displaystyle 0_{\mathrm{}}}$ ${\$는 시간 단위 벡터 필드인 반면 다른 것은 공간과 같은 단위 벡터 필드인 반면, 각 이벤트에서 4개 모두 상호 직교하며 월드 라인이 해당 이벤트를 통과하는 정적 관찰자의 최소 로렌츠 프레임을 결정한다.

$이러한{\displaystyle {\stackrel{}{}}_{}}$ 프레임 필드를 e${\displaystyle {\stackrel{}{}}_{}}$→ ${\displaystyle 3_{\mathrm{}}}$ ${\$ 방향으로$$ 동시에 상승시키면서 랜지빈 관찰자의 물리적 경험을 기술하는 원하는 프레임 필드를 얻는다.

${\displaystyle {\vec {p}}_{0}={\frac {1}{\sqrt {1-\omega ^{2}\,R^{2}}}}\,\partial _{T}+{\frac {\omega \,R}{\sqrt {1-\omega ^{2}\,R^{2}}}}\;{\frac {1}{R}}\partial _{\피 }}$

${\displaystyle {\vec{p}_{1}=\partial _{Z}\;\;{\vec {p}_{2}=\partial _{R}}}}$

${\displaystyle {\vec{p}_{3}={\frac {1}{1}{1}\sqrt {1-\omega ^{2}\,R^{2}}\;{\frac {1}{R}\,\partial _{\\}Phi }+{\frac {\omega \,R}{\sqrt {1-\omega ^{2}\,R^{2}}\,\partial _{T}}}}$

이 틀은 1935년 폴 랜지빈에 의해 처음 소개된 것으로 보인다. 이 틀은 T. A. 베버에 의해 처음으로 명백하게 사용된 것으로 보인다. 1997년! 그것은 영역 0 < R < 1/Ω에 정의된다. 이 한계는 외경 가까이에서 랭귀빈 관측자의 속도가 빛의 속도에 근접하기 때문에 기본적이다.

${\displaystyle {시간}_{\mathrm{}}}$ 단위 벡터 $필드{\displaystyle {\stackrel{}{}}_{}}$ p${\displaystyle {\stackrel{}{}}_{}}$→ 0 ${\$의 각 적분 곡선은 원통형 차트에 일정한 반지름을 가진 나선형(그림 1의 빨간색 곡선 등)으로 나타난다$$. Langevin 관찰자 한 명을 선택하고 각도 속도 Ω으로 단단하게 회전하는 반지름 R의 링에 탑승하는 다른 관찰자를 고려한다고 가정합시다. 그런 다음 공간적 기본 벡터 $p{\displaystyle {\stackrel{}{}}_{}}$→ ${\displaystyle 3_{\mathrm{}}}$ ${\$의 적분 곡선(그림 1의 푸른 나선 곡선$)$을 취하면 링 라이딩 관측자들에게는 "동시의 선"으로 해석될 수 있는 곡선을 얻을 수 있다. 그러나 우리가 그림 1에서 보는 바와 같이, 이러한 고리타분한 관찰자들에 의해 운반되는 이상적인 시계는 동기화될 수 없다. 이것은 회전 원반은커녕 회전 고리에도 만족스러운 공간 기하학의 개념을 정의하는 것이 생각보다 쉽지 않다는 우리의 첫 번째 힌트랍니다!

Langevin concluence의 키네마틱 분해를 계산해 보면 가속 벡터는

${\displaystyle \nabla _{\vec{p}_{0}{\vec{p}_{0}={\frac {-\omega^{2}\,R}{1-\omega^{2}\,R^{2}}\;{\vec{p}_{2}}:}$

이 지점은 반경방향으로 안쪽에 위치하며 각 나선 세계선의 (정수) 반지름에만 의존한다. 팽창 텐셔너는 동일하게 사라지는데, 이는 근처의 랜지빈 관측자들이 서로 일정한 거리를 유지한다는 것을 의미한다. vorticity 벡터는

${\displaystyle {\vec{\\Oomega}{1-\omega^{2}\,R^{2}}\\vec {p}_{1}={\frac {\frac}{\frac}{\\c{p}_{1}}}}}$

대칭의 축과 평행한. 이것은 각 랜지빈 관찰자의 가장 가까운 이웃들의 세계선이 그림 2에서 제시한 바와 같이 자신의 세계선을 중심으로 꼬여가고 있다는 것을 의미한다. 이것은 일종의 "swirling" 또는 vorticity의 지역 개념이다.

이와는 대조적으로, 정적 관찰자의 세계 라인에 직교하는$$ 공간 초고속 $T{\displaystyle }$= ${\displaystyle {T\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\$ 중 하나에 나선형을 투사하면 원이 생성되며, 이는 물론 닫힌 곡선이다. ${\displaystyle {더욱\mathrm{}}_{}}$ 좋은 것은 좌표기준 벡터 $\partial {\displaystyle {\mathrm{}}_{}}$ $∂{\$$Phi }$은 공간과$$ 같은 킬링 벡터 필드로서 적분 곡선이 닫힌 공간 같은 곡선(원, 사실 원)이며, 더욱이 축 R = 0에서 0 길이 닫힌 곡선으로 퇴보한다. 이것은 우리의 스페이스타임이 원통형 대칭을 보이고, 또한 랜지빈 관찰자의 회전에 대한 일종의 세계적인 개념을 나타낸다는 사실을 나타낸다.

그림 2에서 마젠타 곡선은 공간 벡터 p${\displaystyle {\stackrel{}{}}_{}}$→ $2{\displaystyle {\stackrel{}{}}_{}}$, ${\displaystyle p_{\mathrm{}}}$→ 3 ${\$}_{2$},\;{\\vec{p}_{3$$}}$가${\displaystyle {\stackrel{}{}p}_{\mathrm{}}}$ → 1$${\$displaystyle{\vec}}_{$1}(Z$$ 좌표가 필수적이지 $$않기 때문에 그림에서 억제됨)을 나타낸다. 즉 $벡터{\displaystyle {\stackrel{}{}}_{}}$ p${\displaystyle {\stackrel{}{}}_{}}$→ 2${\displaystyle {}_{}}$,${\displaystyle {\stackrel{}{}p}_{\mathrm{}}}$ → ${\displaystyle 3_{\mathrm{}}}$ ${\$는 세계선을 따라 운송되는 페르미-워커가 아니므로$$ 랜지빈 프레임이 비삽입적으로 회전하고 있다. 즉, 랜지빈 프레임의 직접적인 파생에서 우리는 ${\displaystyle {각}_{}}$ 랜지빈 관찰자가 $p{\displaystyle {\stackrel{}{}}_{}}$→ ${\displaystyle 1_{\mathrm{}}}$ ${\displaystyle$$\$$partial _{R}$에 대해 운반하는 프레임의 일정한 속도 회전을 도입함으로써, 만약 우리가 할 수 있다면, 할 수 있었다$.$ 우리는 우리의 프레임이 안정화 된 버전을 얻기를 바랐다.

Born 관리도로 변환

Born 차트를 얻기 위해 간단한 좌표 변환을 사용하여 Langevin 관찰자의 나선형 세계선을 정리한다.

$#\displaystyle t=T,\;\;z=Z,\;\;r=R,\\;\phi =\Phi -\omega \T}$

새로운 선 요소는

${\displaystyle \mathrm {d} s^{2}=-\left(1-\omega ^{2}r^{2}\right)\mathrm {d} t^{2}+2\omega r^{2}\mathrm {d} t\,\mathrm {d} \phi +\mathrm {d} z^{2}+\mathrm {d} r^{2}+r^{2}\mathrm {d} \phi ^{2},}$

$#\displaystyle -\\\z<0><{\frac {1}{\omega}},\-\pi <\phi <\pi }}$

Born 차트가 직교 좌표 차트가 아님을 보여 $주는{\displaystyle \mathrm{}}$ d ${\displaystyle t}$ ${\displaystyle d\mathrm{}}$ ${\displaystyle \varphi }${\$d}t\,\mathrm {$d}\$d} \phi }$과$($와) 관련된 "교차 단자"에 주목하십시오. Born 좌표는 회전 원통 좌표라고도 한다.

새로운 차트에서 랭귀빈 관측자들의 세계선은 수직 직선으로 나타난다. 실제로 랜지빈 프레임을 구성하는 네 개의 벡터 필드를 새 차트로 쉽게 변환할 수 있다. 우리는 얻는다.

${\displaystyle {\vec{p}_{0}={\frac {1}{\sqrt {1-\omega ^{2}\,r^{2}}\,\beca _{t}}}}}$

${\displaystyle {\vec{p}_{1}=\cHB_{z}\;\\\\vec{p}}=\r}}$

${\displaystyle {\vec}_{3}={\frac {1-\omega^{2}\,r^{2}}\}\,\pi }{\phi }}}+{\frac {\omega \}{1-\}}}}},r^{2}}\,\nm_{t}}$

이들은 이전과 정확히 동일한 벡터 필드인데, 이제 단순히 다른 좌표 차트로 표현된다!

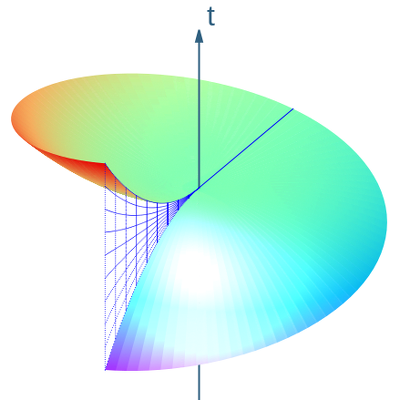
말할 필요도 없이 원통형 차트에서 나선형으로 나타나는 랜지빈 관측기들의 세계선을 '풀어내는' 과정에서 우리는 이제 본 차트에서 나선형으로 나타나는 정적 관측기들의 세계선을 '풀어올린다'는 것이다. 또한 Langevin 프레임과 마찬가지로 Born 차트는 영역 0 < r < 1/Ω에서만 정의된다는 점에 유의하십시오.

If we recompute the kinematic decomposition of the Langevin observers, that is of the timelike congruence ${\displaystyle {\vec {p}}_{0}={\frac {1}{\sqrt {1-\omega ^{2}\,r^{2}}}}\,\partial _{t}}$, we will of course obtain the same answer that we did before, only expressed in terms of the 새 도표 특히 가속 벡터는

${\displaystyle \p}_{\vec{p}_{0}\\\vec {p}_{0}={\frac {-\omega^{2}\,r}{1-\omega^{2}\,r^{2}}\,{\vec{p}_{2}}:$

팽창 시제는 사라지고, vorticity vector는

${\displaystyle {\vec{\\Oomega}{1-\omega ^{2}\,r^{2}}\\vec{p}_{1}={\vec}{p}_{1}}}}$

어떤 프레임 필드에서든 시간 단위 벡터 필드의 이중 코브터 필드는 극소수의 공간적 하이퍼리저를 나타낸다. 그러나, 프로베니우스 통합성 정리는 이러한 공간 초면 요소들을 "함께 결합"하여 합성의 세계 라인과 직교하는 모든 곳에 있는 공간 초면들의 가족을 형성할 수 있는지에 대한 강한 제약을 준다. 실제로, 이것이 가능한 것으로 밝혀졌는데, 이 경우 우리는 쌍성 벡터가 동일하게 사라질 경우에만 결합이 초경직이라고 말한다. 따라서 원통형 차트의 정적 관찰자는 직교 과급자 $T{\displaystyle }$= ${\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$의 고유한 계열을 인정하는 반면$,$ 랭귀빈 관찰자는 그러한 과급자는 인정하지 않는다. 특히 Born 차트의 $공간$ 표면 t${\displaystyle }$= ${\displaystyle {t\mathrm{}}_{}}$ 0 ${\$은 Langevin 관찰자가 아닌 정적 관찰자와 직교한다. 이것은 "회전 디스크의 공간 기하학"을 정의하는 것이 생각보다 간단하지 않다는 두 번째(그리고 훨씬 더 중요한) 지표다.

이 중요한 점을 더 잘 이해하려면 세 번째 Langevin 프레임 벡터의 적분 곡선을 고려하십시오.

${\displaystyle {\vec {p}}_{3}={\sqrt {1-\omega ^{2}\,r^{2}}}\,{\frac {1}{r}}\,\partial _{\phi }+{\frac {\omega \,r}{\sqrt {1-\omega ^{2}\,r^{2}}}}\,\partial _{t}}$

$radius{\displaystyle }$= ${\displaystyle 0,}$ ${\displaystyle t}$= ${\displaystyle 0}$,$$t = 0 {\$displaystyle$\phi $=0,\,t=0}$을(를) 통과한다.(편의를 위해 우리는 논의에서 본질적이지 않은 좌표 z를 억제할 것이다$.)$ 이 곡선은 표면에 놓여 있다.

${\displaystyle \phi +\bega \,t-{\frac {t}{\\\omega \,r^}=0,\;\;\-\pi <\pi \pi }$

그림 3과 같다. 우리는 이것을 랜지빈 관측자들에게 "한 번에 하나의 공간"으로 간주하고 싶다. 하지만 두 가지가 잘못된다.

첫째, 프로베니우스 정리는 $p{\displaystyle {\stackrel{}{}}_{}}$→ ${\displaystyle 2_{\mathrm{}}}$,${\displaystyle {\stackrel{}{}p}_{\mathrm{}}}$ → 3 ${\$3}}}이$$ 공간적 과장이 전혀 없는 것과 접하고 있음을 말해준다. 실제로 초기 반지름을 제외하고 벡터 $p{\displaystyle {\stackrel{}{}}_{}}$→ ${\displaystyle 2_{\mathrm{}}}$ ${\$}}개는 우리 쪽 슬라이스에 놓여 있지 않다$$. 그래서, 우리가 공간적 초주형 얼굴을 발견하는 동안, 그것은 오직 몇몇 랜지빈 관찰자들의 세계선과 직교한다. 프로베니우스 정리로부터의 방해는 $벡터장{\displaystyle {\stackrel{}{}}_{}}$ p${\displaystyle {\stackrel{}{}}_{}}$→ ${\displaystyle 2_{\mathrm{}}}$, p${\displaystyle {\stackrel{}{}}_{}}$→ ${\displaystyle 3_{\mathrm{}}}$ ${\$p}}}}}},\\\vec {p}}{$3}}}$의 실패 측면에서 이해할 수 있기 때문에 이 방해는 사실 리 이론이다. 즉, 그것은 회전하는 관찰자들에게 공간과잉에 대한 만족스러운 개념의 존재에 대한 일종의 극소수의 방해물이다.

둘째, 그림 3에서 알 수 있듯이, 우리의 시도된 과플라이스는 적분 곡선(파란색 그리드 불연속성으로 표시)의 "점프"로 인해 "시간"이라는 불연속적인 개념을 초래할 것이다. 그 대신에, 우리는 다중값의 시간을 사용하려고 시도할 수 있다. 이러한 대안들 중 어느 것도 그다지 매력적이지 않아 보인다! 이것은 명백히 전세계적인 방해물이다. 이것은 물론 우리가 하나의 링(디스크의 테두리)을 타고 있는 랜지빈 관찰자의 시계를 동기화하지 못한 결과로서, 전체 디스크는 훨씬 더 적다.

사그낙 효과

우리가 일정한 각속도 Ω으로 회전하는 고리 둘레에 광섬유 케이블을 고정했다고 상상해 보라. 우리는 링 라이딩 관찰자가 측정한 대로 케이블 주위로 시계방향과 시계 반대방향으로 전송되는 레이저 펄스에 대한 왕복 여행 시간을 계산하고자 한다. 간단히 말해서, 우리는 빛이 진공에서 빛의 속도보다 다소 낮은 속도로 광섬유 케이블을 통해 이동한다는 사실을 무시하고, 우리 레이저 펄스의 세계선이 null 곡선(확실히 null Geodesic은 아니다!)인 것처럼 가장할 것이다.

Born 선 요소에 ${\displaystyle d}$ s${\displaystyle }$= ${\displaystyle d}$ z${\displaystyle }$= ${\displaystyle d}$ ${\displaystyle r\mathrm{}}$= ${\displaystyle 0}$ ${\daystyle \mathrmat {d}s=\mathrm$ {$d} z=\mathrmat {d} r=0}$을(를) 넣자$.$ 이것으로 알 수 있다.

${\displaystyle(1-\omega^{2}\,r_{0}^{2},\mathrm {d} t^{2}=2\mote \,r_{0}^{2},\mathrm {d} \phi +r_{0}^{0}}}\,\mathr} \{d} \pi \pi \{{{{{di \{pi^{d}{pi^{d}{{{{{{{{{{{{{{{{{{{$

또는

${\displaystyle \mathrm {d} t_{+}={\frac {r_{0}\,\mathrm {d} \phi }{1-\omega \,r_{0}}},\quad \mathrm {d} t_{-}=-{\frac {r_{0}\,\mathrm {d} \phi }{1+\omega \,r_{0}}}}$

우리는 왕복 여행 시간을 얻는다.

${\displaystyle \Delta t_{+}=\int _{0}^{2\pi }{\frac {r_{0}\,\mathrm {d} \phi }{1-\omega \,r_{0}}}={\frac {2\pi r_{0}}{1-\omega \,r_{0}}},\quad \Delta t_{-}=\int _{0}^{-2\pi }-{\frac {r_{0}\,\mathrm {d} \phi }{1+\omega \,r_{0}}}={\frac {2\pi r_{0}}{1+\omega \,r_{0}}}}$

Putting ${\displaystyle \delta ={\frac {\Delta t_{+}-\Delta t_{-}}{2\,\pi \,r_{0}}}}$, we find ${\displaystyle \omega _{+,-}={\frac {-1\pm {\sqrt {1+\delta ^{2}}}}{r_{0}\,\delta }}}$ (positive ω means counter-clockwise rotation, negative Ω은 시계 방향 회전을 의미하며, 따라서 고리 방향 관찰자는 시계 방향과 시계 반대 방향 이동 시간 사이의 차이에서 (정적 관찰자가 측정한 대로) 링의 각도 속도를 결정할 수 있다. 이것은 Sagnac 효과라고 알려져 있다. 그것은 분명히 세계적인 효과다.

Null Geodesics

우리는 원통형 차트와 Born 차트의 null 지오데틱의 외관을 비교하고 싶다.

원통형 차트에서 지오데틱 방정식은

${\displaystyle {\ddot {T}}=0,\;\;{\ddot {Z}}=0,\;\;{\ddot {R}}-R\,{\dot {\Phi }}^{2}=0,\;\;{\ddot {\Phi }}+{\frac {2}{R}}\,{\dot {\Phi }}\,{\dot {R}}=0.}$

우리는 즉시 첫 번째 통합을 얻는다.

${\dot스타일 {\T}=E,\;\;{\dot{Z}=P,\;\;\;\\\dot{\Phi}}}={\frac {L}{R^{2}}.}$

$d{\displaystyle \mathrm{}}$ ${\displaystyle s{}^{}}$ ${\displaystyle 2{}^{}}$= 0 ${\displaystyle \mathrm {d}s^{2}=0}$을(를) 설정하여 라인 요소에서 얻은 식에 연결하면 다음과 같은 결과를 얻을 수 있다$.$

${\displaystyle {\dot{R}^{2}=E^{2}-P^{2}-{\frac {L^{2}}:{R^{2}}\geq 0}$

여기서 우리는 null 지오데틱의 최소 반경이 에 의해 주어지는 것을 본다.

${\displaystyle E^{2}-P^{2}-{\frac {L^{2}}{R_{\mathrm {min} }^{2}}}=0\quad }$ i.e., ${\displaystyle \quad R_{\mathrm {min} }={\frac { L }{\sqrt {E^{2}-P^{2}}}}}$

이 때문에

${\displaystyle {\dot{R}^{2}=L^{2}\왼쪽({\frac {1}{R_{\mathrm {min}{}^{2}}-{\frac {1}{R^{R^}}}\오른쪽).}$

이제 다음과 같이 아핀 파라미터에 의해 파라미터화된 곡선으로 Null Geodics를 얻는 것을 해결할 수 있다.

${\displaystyle {\reasoned}R&={\sqrt {(E^{2}-P^{2})\,s^{2}+L^{2}/(E^{2}-P^{2})}}=\\&={\sqrt {(E^{2}-P^{2})\,s^{2}+R_{\mathrm {min} }^{2}}},\\T&=T_{0}+E\,s,\\[1em]Z&=Z_{0}+P\,s,\\\Phi &=\Phi _{0}+\operatorname {arctan} \좌({\frac {E^{2}-P^{2}}:L}\,s\우)=\\&=\Phi _{0}+\operatorname {arctan} \좌({\frac {\sqrt {E^{2}-P^{2}}:{R_{\\mathrm {min}}\}\,\operatorname {sgn}}},s\오른쪽).\end{정렬}}}$

우리의 목적에 더 유용한 것은 null 지오데틱의 궤적(그 궤적이 어떤 공간적 과부하${\displaystyle }T{\displaystyle }$ = ${\displaystyle {T\mathrm{}}_{}}$ ${\displaystyle {}_{}}${\$displaystyle$T=$T_{0$은 물론 직선이라는 관측이다.

${\displaystyle R=R_{\mathrm {min}\,\sec(\Phi -\Phi _{0}).}$

두 지점(원점에 가장 가까운 지점의 같은 측면)을 통해 선의 최소 반경을 얻기 위해, 우리는 해결한다.

${\displaystyle R_{1}=R_{\mathrm {min} }\,\sec(\Phi _{1}-\Phi _{0})\;\;\;R_{2}=R_{}=R_{\mathrm {min}\}\sec(\Phi _{2}-{0}$

어떤 것을 주는지

${\displaystyle R_{\mathrm {min} }={\frac {R_{1}\,R_{2}\, \sin(\Phi _{2}-\Phi _{1}) }{\sqrt {R_{1}^{2}-2\,R_{1}\,R_{2}\,\cos(\Phi _{2}-\Phi _{1})+R_{2}^{2}}}}.}$

이제 가장 간단한 경우, 방사형 null 지오데틱스(R_min = L = 0, E = 1, P = 0)를 고려하십시오. 외측 바운드 방사상 Null 지오디자크는 양식으로 작성될 수 있다.

${\displaystyle T=s,\;Z=Z_{0},\;R=s,}$

${\displaystyle \Phi =\mathrm {const.}} =\omega \,R_{0}}$

링 라이딩 랜지빈 관찰자(그림 4₀ 참조)의 반지름 R과 함께. Born 차트로 변환하여, 우리는 궤적이 다음과 같이 기록될 수 있음을 발견한다.

${\displaystyle r=r_{0}-{\frac {\phi }{\omega }}.}$

이 트랙은 Born 차트에서 약간 구부러진 것으로 나타난다(그림 4의 녹색 곡선 참조). 섹션 변환에서 본 차트로, 우리는 이러한 "추적"을 Langevin 관찰자의 경우 t = t에₀ 대한 직교 과장이 존재하지 않기 때문에 Born 차트에서 이러한 "추적"을 "거부"로 적절하게 언급할 수 없다(그림 3 참조).

마찬가지로 내부 경계 방사형 Null 지오데틱에서도

${\displaystyle r={\frac {\phi }{\omega }}}$

그림 4에서 빨간색 곡선으로 묘사되었다.

R = 0에서 고정된 관찰자 S를 향해 레이저 펄스를 보내려면 Langevin 관찰자 L이 자신의 움직임을 교정하기 위해 약간 뒤에 조준해야 한다는 점에 유의하십시오. 오리 사냥꾼이 예상하는 것처럼 사물을 돌리면 시계 반대방향 회전 링을 타고 랜지빈 관찰자를 향해 레이저 펄스를 보내려면 중앙 관찰자가 조준해야 하는데, 이 관찰자의 현재 위치가 아니라 신호를 가로채기 위해 제 시간에 도착할 위치에 있어야 한다. 내향 및 외향 경계가 있는 방사상 Null 지오데틱 계열은 스페이스타임에 매우 다른 곡선을 나타내며, 이들의 투영은 Ω > 0에 대해 일치하지 않는다.

마찬가지로, 링 라이딩 랜지빈 관측자 사이의 null 지오디컬은 회전 방향에 따라 지오디컬이 전파되는 경우 Born 차트에서 안쪽으로 약간 구부러진 것처럼 보인다(그림 5의 녹색 곡선 참조). 이를 보려면 원통형 차트에 null Geodesic 방정식을 양식으로 작성하십시오.

${\displaystyle T=R_{\mathrm {min}\,\tan(\Phi ),}$

${\displaystyle R=R_{\mathrm {min}\,\sec(\Phi).}$

Born 좌표로 변환하여 방정식을 구함

${\displaystyle t=r_{\\mathrm {min}\,\tan(\phi +\omega \,t),}$

${\displaystyle r=r_{\mathrm {min}\,\sec(\phi +\omega \,t)}$

ϕ을 제거하면 얻을 수 있다.

${\displaystyle r={\sqrt {r_{\mathrm {min}}^{2}+t^{2}}}}}$

이는 지오데틱이 실제로 안쪽으로 구부러지는 것처럼 보인다는 것을 보여준다(그림 6 참조). 우리는 또한 그것을 발견한다.

${\displaystyle \phi =-\omega \,t+\bename {arctan}(t/r_{\mathrm {min} })}$

회전 반대 방향으로 전파되는 null 지오데틱의 경우(그림 5의 빨간색 곡선)

${\displaystyle r={\sqrt {r_{\mathrm {min}}^{2}+t^{2}}}},}$

${\displaystyle \phi =-\omega \,t-\bename {arctan}(t/r_{\mathrm {min}})$

그리고 지오데틱은 약간 바깥쪽으로 구부러진다. 이것은 모든 null 지오디지컬이 방사형이거나 원통형 대칭 축에 가장 가까운 어떤 지점을 가지기 때문에 Born 차트에서 null 지오디지컬의 외관에 대한 설명을 완성한다.

참고(그림 5 참조) 다른 링 라이딩 관찰자에게 레이저 펄스를 보내려는 링 라이딩 관찰자는 대상의 회전 운동을 보상하기 위해 Born 차트에 주어진 각 좌표보다 약간 앞이나 뒤쪽으로 조준해야 한다. 또한 여기에 제시된 그림은 움직이는 관찰자가 자신의 천체에 있는 다른 물체의 외관상 위치가 자신의 움직임 방향을 향해 이동되는 것을 볼 것이라는 우리의 기대(밤하늘의 모습 참조)와 완전히 호환된다는 점에 유의하십시오.

대형의 레이더 거리

평탄한 시간에도 가속 관측자(선형 가속 관측자, 린들러 좌표 참조)는 다양하지만 작동상 유의한 거리에 대한 다양한 개념을 채택할 수 있는 것으로 나타났다. 아마도 이것들 중 가장 간단한 것은 레이더 거리일 것이다.

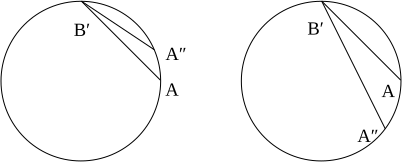
R=0의 정적 관찰자가 R = R의₀ 링 라이딩 관찰자와의 거리를 어떻게 결정할 수 있는지 생각해 보십시오. 이벤트 C에서 그는 A′의 링 라이딩 관찰자의 월드 라인에 부딪힌 다음 이벤트 C″에서 중앙 관찰자에게 되돌아간다(그림 7의 우측 다이어그램 참조). 그런 다음 그는 (그가 가지고 있는 이상적인 시계에 의해 측정된) 경과 시간을 2로 나눈다. 그가 이 거리에 대해 단순히 R₀(원통형 차트에서) 또는 R₀(Born 관리도에서)을 얻는다는 것은 어렵지 않다.

마찬가지로 링 라이딩 관찰자는 이벤트 C에서 자신의 세계선을 타격하고 이벤트 A에서 링 라이딩 관찰자에게 되돌아오는 이벤트 A에서 레이더 펄스를 보내 중앙 관찰자까지의 거리를 결정할 수 있다(그림 7의 왼쪽 그림 참조). It is not hard to see that he obtains for this distance ${\displaystyle R_{0}{\sqrt {1-\omega ^{2}\,R_{0}^{2}}}}$ (in the cylindrical chart) or ${\displaystyle r_{0}{\sqrt {1-\omega ^{2}\,r_{0}^{2}}}}$ (in the Born chart), a result which is somewhat smaller than 중앙 관찰자가 얻은 것 이는 시간 확장의 결과: 링 라이딩 관찰자의 경과 시간은 중앙 관찰자의 시간보다$$ 1 -${\displaystyle \sqrt{{}^{}}}$ 2 ${\displaystyle \sqrt{r{}^{}{}_{}^{}}}$ ${\displaystyle \sqrt{{0\mathrm{}}_{}^{}}}$ ${\displaystyle \sqrt{{\mathrm{}}_{}^{}}}$ ${\$배수만큼 더 작다. 따라서 레이더 거리는 단순한 운용상 중요성이 있지만 대칭조차 되지 않는다.

이 중요한 지점을 운전하기 위해, 두 링 라이딩 관측자가 얻은 레이더 거리를 방사형 좌표 R = R과₀ 비교한다. 그림 8의 왼쪽 다이어그램에는 사건 A의 좌표를 다음과 같이 기록할 수 있다.

${\displaystyle T=0,\;Z=0,\;X=R_{0},Y=0}$

그리고 우리는 사건 B의 좌표를 다음과 같이 쓸 수 있다.

${\displaystyle T=2\,R_{0}\,\sin \left({\frac {\Phi }{2}}\right),\;Z=0,}$

$[\displaystyle X=R_{0}\cos(\Phi )]\;Y=R_{0}\sin(\Phi )}$

알 수 없는 경과된 적정 시간을 ${\displaystyle \mathrm{\Delta s}}$ ${\displaystyle \Delta$ s$}$로 기록하면서 이제 이벤트 A의 좌표를 Δs {\displaystyle \Delta s}로 기록한다$.$

${\displaystyle T={\frac {\delta s}{\sqrt {1-\omega^{2}\,R_{0}^{2}},\;Z=0}$

${\displaystyle X=R_{0}\cos \left({\frac {\omega \,\Delta s}{\sqrt {1-\omega ^{2}\,R_{0}^{2}}\오른쪽)\;Y=R_{0}\sin \left({\frac {\omega \,\Delta s}{\sqrt {1-\omega ^{2}\,R_{0}^{2}}\오른쪽)}}$

이러한 사건을 연결하는 선분할을 null로 요구함으로써 Δs에 대해 원칙적으로 해결할 수 있는 방정식을 얻는다. 이 절차는 다소 복잡한 비선형 방정식을 제공한다는 것이 밝혀졌기 때문에 우리는 단지 몇 가지 대표적인 수치 결과를 제시한다. R₀ = 1, φ = π/2, Ω = 1/10로, A에서 B까지의 레이더 거리는 약 1.311인 반면 B에서 A까지의 거리는 약 1.510인 것을 알 수 있다. Ω이 0을 나타내는 경향이 있기 때문에, 두 결과 모두 22 = 1.414를 지향한다(그림 5 참조).

이러한 불일치를 억제할 수 있지만, 랑게빈 관찰자 한 명 또는 심지어 밍코스키 스팩타임에 임의로 가속하는 관찰자 한 명의 신체적 경험을 기술하는 데 적응한 좌표도를 고안하는 것은 결코 불가능한 일이 아니다. Pauri와 Vallisneri는 Mérzke-Wheeler 좌표라고 부르는 적응된 좌표를 고안하기 위해 Mérzke-Wheeler 시계 동기화 절차를 수정했다(아래 인용된 논문 참조). 일정한 원형 움직임의 경우, 이 차트는 사실 주어진 랜지빈 관찰자로부터의 레이더 거리 개념 "대규모"와 매우 밀접하게 관련되어 있다.

소형 레이더 거리

위에서 언급했듯이, 랭귀빈 관찰자 가족은 다양한 이유로 직교 과민증을 인정하지 않는다. 따라서 이러한 관찰자들은 단순히 연속적인 "일정한 시간 조각"의 가족으로 스페이스타임의 슬라이싱과 연관될 수 없다.

그러나, 랜지빈 합성이 정지되어 있기 때문에, 우리는 이 합성의 각 세계선을 한 점씩 교체하는 것을 상상할 수 있다. 즉, 3차원 위상학적 다지관인 란제빈 일치에 의한 민코프스키 스페이스타임(또는 오히려 영역 0 < R < 1/Ω))의 지수 공간을 고려할 수 있다. 더 좋은 것은, 이 지수의 다지관에 리만 미터법을 배치하여, 3차원 리만 다지관으로 바꾸어, 그 미터법이 단순한 운용상의 의의를 갖도록 할 수 있다.

이를 보려면 Born 선 요소를 고려하십시오.

${\displaystyle \mathrm {d} s^{2}=-(1-\omega ^{2}\,r^{2})\,\mathrm {d} t^{2}+2\,\omega \,r^{2}\,\mathrm {d} t\,\mathrm {d} \phi +\mathrm {d} z^{2}+\mathrm {d} r^{2}+r^{2}\,\mathrm {d} \phi ^{2},}$

${\displaystyle -\\pi.t, z<\flatty,\\;0<{\frac{1}{\omega},\;\;\-\pi <\phi <\pi .}}$

ds² = 0 설정 및 dt에 대한 해결

${\displaystyle \mathrm {d} t_{+}={\frac {\omega \,r^{2}\,\mathrm {d} \phi +{\sqrt {(1-\omega ^{2}\,r^{2})\;(\mathrm {d} z^{2}+\mathrm {d} r^{2})+r^{2}\,\mathrm {d} \phi ^{2}}}}{1-\omega ^{2}\,r^{2}}},}$

${\displaystyle \mathrm {d} t_{-}={\frac {\omega \,r^{2}\,\mathrm {d} \phi -{\sqrt {(1-\omega ^{2}\,r^{2})\;(\mathrm {d} z^{2}+\mathrm {d} r^{2})+r^{2}\,\mathrm {d} \phi ^{2}}}}{1-\omega ^{2}\,r^{2}}}.}$

Langevin 관찰자에 의해 방출된 왕복 레이더 블립의 경과된 적절한 시간은 그 다음이다.

${\displaystyle {\sqrt {1-\omega ^{2}\,r^{2}}}\;{\frac {\mathrm {d} t_{+}-\mathrm {d} t_{-}}{2}}={\sqrt {\mathrm {d} z^{2}+\mathrm {d} r^{2}+{\frac {r^{2}\,\mathrm {d} \phi ^{2}}{1-\omega ^{2}\,r^{2}}}}}.}$

그러므로 우리의 지분의 다지관에는 리만 라인 원소가 있다.

${\daystyle \mathrm {d} \mathrm {d}^{2}=\mathrm {d}z^{2}+{\frac {r^{2}\\d}\mathrm {d} \phi ^{1}{1-\omega{2}\,r^{2}}}}}}}}}}$

$[\\displaystyle -\pi ][nothy]\\\\frac {1}{\1}{\omega },\;\;\\pi <\phi <\pi }}]$

극심하게 가까운 랭귀빈 관측자 사이의 거리에 해당한다. 우리는 이것을 랜지빈-란다우-라이프시츠 미터법이라고 부를 것이고, 우리는 거리 레이더 거리의 개념을 "작은 것"이라고 부를 수 있다.

이 측정 기준은 랜지빈에 의해 처음 제시되었지만, 레이더 거리 측면에서 "작은 것"에 대한 해석은 레브 랜도와 에브게니 리프시츠에 기인한다. 그는 어떤 로렌츠 다지관의 지수를 위해 고정된 시간적 일치에 의해 작업하도록 건설을 일반화했다.

우리가 코프레임을 채택한다면

${\displaystyle \theta ^{\hat {1}}=\mathrm {d} z,\;\;\theta ^{\hat {2}}=\mathrm {d} r,\;\;\theta ^{\hat {3}}={\frac {r\,\mathrm {d} \phi }{\sqrt {1-\omega ^{2}\,r^{2}}}}}$

우리는 우리의 3차원 지수 다지관의 리만 곡률 텐서(tensor)를 쉽게 계산할 수 있다. 두 개의 독립적인 비경쟁적 구성 요소만 가지고 있으며,

${\displaystyle {R^{\hat {2}}}_{{\hat {3}}{\hat {2}}{\hat {3}}}={\frac {-3\,\omega ^{2}}{(1-\omega ^{2}r^{2})^{2}}}=-3\,\omega ^{2}+O(\omega ^{4}\,r^{2}),}$

${\displaystyle {R^{\hat {3}}}_{{\hat {2}}{\hat {3}}{\hat {2}}}={\frac {-3\,\omega ^{2}\,r^{2}}{(1-\omega ^{2}r^{2})^{3}}}=-3\,\omega ^{2}\,r^{2}+O(\omega ^{4}\,r^{4}).}$

따라서 어떤 의미에서는 테오도르 칼루자의 주장대로 1910년에 이르면 (증거 없이) 회전 원반의 기하학이 곡선이다. 실제로 Ω으로 2차 순서까지 그것은 칼루자의 주장대로 쌍곡면의 기하학을 가지고 있다.

경고: 우리가 본 바와 같이, 랑게빈 관찰자가 경직된 회전식 디스크에 탑승하여 사용할 수 있는 거리에 대한 많은 개념들이 있으므로, "회전식 디스크의 기하학"을 언급하는 문구는 항상 세심한 검증이 필요하다.

이 중요한 지점을 되돌리기 위해, 랜도-라이프시츠 측정 지표를 사용하여 반지름 R이₀ 있는 링을 타는 랜지빈 관찰자와 중앙 정적 관찰자 사이의 거리를 계산해 봅시다. 이를 위해서는 적절한 null 지오데틱 트랙 위에 우리의 라인 요소만 통합하면 된다. 이전 작업에서 우리는 플러그를 꽂아야 한다는 것을 알았다.

${\daystyle \mathrm {d} r={\frac {\mathrm {d} \phi }{\omega },\\mathrm {d} z=0}$

우리의 라인 요소와 통합으로

${\displaystyle \int _{0}^{\델타 }\mathrm {d} \sigma =\int \limits _{0}^{r_{0}}{0}{0}}}{{0+{\frac {\omega ^{2}r^{2}}}}{1-\omega ^{2}}}}}\mathrmat {d} r}}}}}}.$

이것으로 알 수 있다.

${\displaystyle \Delta =\int _{0}^{r_{0}}{\frac {\mathrm {d} r}{\sqrt {1-\omega ^{2}\,r^{2}}}}={\frac {\arcsin(\omega r_{0})}{\omega }}=r_{0}+{\frac {\omega ^{2}\,r_{0}^{3}}{6}}+O(r_{0}^{5}).}$

현재 우리는 리만 측정법을 다루고 있기 때문에, 이 거리에 대한 개념은 "대부분의" 레이더 거리와는 달리, 물론 두 관측자를 서로 바꾸어 놓고 보면 대칭적이다. 이 개념에 의해 주어진 값은 이전 절에서 계산한 "대규모" 레이더 거리와 모순된다. 또한 란다우-리프시츠 메트릭스가 2차까지 아인슈타인 동기화 규칙에 동의하기 때문에 방금 계산한 곡률 텐서(tensor)는 작동상 중요한 의미를 가지고 있음을 알 수 있다. 반면에 랑게빈 관찰자 쌍들 사이의 레이더 거리는 확실히 리만족 개념의 거리, 쌍들 사이의 거리는 아니다. 인근 랭귀빈 관측자 중 하나는 랭귀빈-랜도-라이프시츠 측정기준에 의해 주어진 리만니아 거리에 해당된다. (하워드 퍼시 로버트슨의 충실한 구절에서 이것은 클라인렌의 운동학이다.)

우리 랜지빈 관측자들의 공간 거리에 대한 모든 합리적인 관념이 인근 관측자들에게 동의한다는 것을 알 수 있는 한 가지 방법은, 네이단 로젠에 이어, 어떤 랜지빈 관찰자의 경우, 즉각적으로 동시에 움직이는 관성 관측자는 아주 작은 거리에 대해서도 란지빈-란도-라이프시츠 측정계에 의해 주어진 거리를 얻을 수 있다는 것을 보여주는 것이다.

참고 항목

• Ehrenfest 역설은 때때로 논란이 되는 주제를 위해 Born 차트를 사용하여 종종 연구했다.
• 광섬유 자이로스코프
• 린들러는 Minkowski spacetime에서 다른 중요한 가속도 관찰자군에 적응된 유용한 좌표도를 위해 좌표를 정한다. 이 기사는 또한 그러한 관찰자가 사용할 수 있는 거리에 대한 뚜렷한 개념의 존재를 강조한다.
• 사그낙 효과

참조

역사적으로 관심이 있는 몇 가지 논문:

• Born, M. (1909). "Die Theorie des starren Elektrons in der Kinematik des Relativitäts-Prinzipes". Ann. Phys. 30 (11): 1–56. Bibcode:1909AnP...335....1B. doi:10.1002/andp.19093351102.
  • Wikisource 변환: 상대성 원리의 운동학적 강체 전자 이론
• Ehrenfest, P. (1909). "Gleichförmige Rotation starrer Körper und Relativitätstheorie". Phys. Z. 10: 918. Bibcode:1909PhyZ...10..918E.
  • Wikisource 변환: 강체의 균일한 회전과 상대성 이론
• Langevin, P. (1935). "Remarques au sujet de la Note de Prunier". C. R. Acad. Sci. Paris. 200: 48.

몇 가지 고전적인 언급:

• Grøn, Ø. (1975). "Relativistic description of a rotating disk". Am. J. Phys. 43 (10): 869–876. Bibcode:1975AmJPh..43..869G. doi:10.1119/1.9969.
• Landau, L. D. & Lifschitz, E. M. (1980). The Classical Theory of Fields (4th ed.). London: Butterworth-Heinemann. ISBN 0-7506-2768-9. 정지 일치에 의한 로렌츠 다지관의 지수에 대한 Landau-Lifschitz 측정기준은 섹션 84를 참조한다. Langevin 관찰자에 대한 적용은 섹션 89의 끝부분의 문제를 참조한다.

선택한 최근 원본:

• Rizzi, G. & Ruggiero, M. L. (2004). Relativity in Rotating Frames. Dordrecht: Kluwer. ISBN 1-4020-1805-3. 이 책에는 외빈드 그뢰른과 에렌페스트의 역설과 관련 논쟁에 관한 몇몇 논문들의 귀중한 역사적 조사와 랑게빈 일치에 대해 논하는 류이 벨의 논문이 실려 있다. 이 책에서 수백 개의 추가 참고문헌을 찾을 수 있을 것이다.
• Pauri, Massimo & Vallisneri, Michele (2000). "Märzke-Wheeler coordinates for accelerated observers in special relativity". Found. Phys. Lett. 13 (5): 401–425. Bibcode:2000gr.qc.....6095P. doi:10.1023/A:1007861914639. S2CID 15097773. 단일 Langevin 관찰자의 "대규모" 레이더 거리를 사용하여 구성된 좌표도를 연구한다. eprint 버전을 참조하십시오.

외부 링크

• 마이클 와이스(1995)의 상대성 강체 회전 디스크.물리 FAQ.