이완 발진기

전자공학에서 이완 오실레이터는 삼각파 또는 사각파 등 비비무소이드 반복 출력 신호를 생성하는 비선형 전자 오실레이터 회로다.^[1][2][3][4] 회로는 트랜지스터, 비교기, 릴레이, ^[5]op 앰프와 같은 스위칭 소자 또는 터널 다이오드와 같은 음극 저항 소자를 포함하는 피드백 루프로 구성되며, 임계 수준에 도달할 때까지 저항을 통해 콘덴서 또는 인덕터를 반복적으로 충전한 다음 다시 방출한다.^[4][6] 오실레이터의 주기는 커패시터 또는 인덕터 회로의 시간 상수에 따라 달라진다.^[2] 활성 장치는 충전 모드와 방전 모드 사이를 갑자기 전환하여 연속적으로 변화하는 반복 파형을 생성한다.^[2][4] 이는 다른 유형의 전자 오실레이터인 고조파 또는 선형 오실레이터와 대비되는데, 이 오실레이터는 피드백이 있는 앰프를 사용하여 공명기의 공명 진동을 자극하여 사인파를 생성한다.^[7] 이완 오실레이터는 깜박이는 조명(턴 신호)과 전자 신호기, 전압 제어 오실레이터(VCO), 인버터 및 스위칭 전원 공급기, 디지털 컨버터와 아날로그 듀얼 슬로프, 함수 발생기 등의 응용 프로그램을 위한 저주파 신호를 생성하는 데 사용된다.

이완 오실레이터라는 용어는 비선형 진동을 생성하는 과학의 많은 다양한 영역의 동적 시스템에도 적용되며 전자 이완 오실레이터와 동일한 수학적 모델을 사용하여 분석할 수 있다.^{[8][9][10][11]} earthquakes,[12]분필 한 blackboard,[14]에 소리 포식자와 먹이 동물의 주기적인 사람들 유전자 활성화 systems[9]로 모델로 삼고 예를 들어, 신경 cells,[11]온도 조절 장치 사격의 지열 geysers,[12][13]네트워크 난방 systems,[14]결합된 화학 reactions,[9]는 인간 heart,[11][14]을 조절한다.휴식 oscillators. 이완 진동은 서로 다른 시간 척도에서 두 개의 과정이 번갈아 일어나는 것이 특징이다. 즉, 평형점에 접근하는 시스템이 평형점에 접근하는 긴 이완 기간과 평형점이 이동하는 짧은 충동 기간이 번갈아 나타난다.^{[11][12][13][15]} 이완 오실레이터의 기간은 주로 이완 시간 상수에 의해 결정된다.^[11] 이완 진동은 한계 사이클의 한 유형이며 비선형 제어 이론에서 연구된다.^[16]

전자 이완 오실레이터

첫번째 완화 발진기 회로, 비안정 멀티 바이브레이터, 앙리 아브라함에 의해 그리고 유진이 블로흐 세계 대전 I.[17][18]발타자르 동안 van der 진공 튜브 조화 진동에서 폴 처음으로 저명한 휴식 진동을 사용하여 발명되고, rel의 첫번째 수학적 모델에서 파생된 용어"완화 발진기"시작되었다.axation 1920년 영향력 있는 Van der Pol 오실레이터 모델인 오실레이터.^[18][19][20] 반 데어 폴은 역학으로부터 이완이라는 용어를 빌렸다; 콘덴서의 방전은 응력 이완의 과정, 변형이 점진적으로 사라지고 비탄력적인 매체에서 평형으로 돌아오는 과정과 유사하다.^[21] 이완 발진기는 두 등급으로^[13] 나눌 수 있다.

• 톱니, 스위프 또는 플라이백 오실레이터: 이 유형에서 에너지 저장 콘덴서는 천천히 충전되지만 본질적으로 스위칭 소자를 통한 단락에 의해 급속하게, 즉 즉시 방전된다. 따라서 출력 파형에는 사실상 전체 주기를 차지하는 "램프"가 하나만 있다. 콘덴서를 통과하는 전압은 톱니 파형에 근접한 반면, 스위칭 소자를 통과하는 전류는 짧은 펄스의 연속이다.
• 예측 가능한 멀티비브레이터: 이 형식에서 콘덴서는 저항을 통해 천천히 충전 및 방전되므로 출력 파형은 증가하는 램프와 감소하는 램프라는 두 부분으로 구성된다. 캐패시터를 통과하는 전압은 삼각 파형에 근접한 반면, 스위칭 소자를 통한 전류는 사각 파형에 근사한다.

적용들

이완 오실레이터는 일반적으로 깜박이는 조명, 전자 신호기 및 일부 디지털 회로에서 시계 신호와 같은 용도의 저주파 신호를 생성하는데 사용된다. 진공관 시대에는 CRT 오실로스코프의 전자 기관과 수평 편향 회로 및 타임 베이스에서 오실레이터로 사용되었는데, 가장 일반적인 것 중 하나는 매우 선형적인 램프를 만들기 위해 진공관을 정전류 소스로 사용하는 Alan Blumlein에 의해 발명된 밀러 집적기 회로였다.^[22] 또한 전압 제어 오실레이터(VCO),^[23] 인버터 및 스위칭 전원 공급 장치, 디지털 컨버터에 대한 이중 슬로프 아날로그, 사각파 및 삼각파를 생성하기 위한 함수 발생기에도 사용된다. 이완 오실레이터는 선형 오실레이터보다 설계가 용이하고 LC 오실레이터와 같은 인덕터가 필요하지 않아 집적회로 칩에서 제작이 용이하며 ^[23][24]넓은 주파수 범위에서 튜닝이 가능하기 때문에 널리 사용된다.^[24] 그러나 선형 오실레이터보다 위상 노이즈가^[23] 많고 주파수 안정성이 떨어진다.^[2][23] 마이크로일렉트로닉스가 등장하기 전에는 단순 이완 오실레이터는 종종 흉선관,^[22] 네온 램프,^[22] 또는 무작동 트랜지스터와 같은 이력(hysteresis)이 있는 음저항 소자를 사용했지만, 오늘날에는 555 타이머 칩과 같은 전용 집적회로(integrated circuit)로 제작되는 경우가 더 많다.

피어슨-안손 발진기

이 예는 정전류 또는 전압 선원에 의해 구동되는 정전용량 또는 저항용 용량성 집적 회로와 콘덴서와 병렬로 연결된 이력(니온 램프, 티라트론, 다이락, 역편향 양극성 트랜지스터 ^[25]또는 단작동 트랜지스터)을 가진 임계 소자로 구현할 수 있다. 커패시터는 입력 소스에 의해 충전되어 커패시터의 전압이 상승한다. 임계 장치는 커패시터 전압이 임계값(트리거) 전압에 도달할 때까지 전혀 수행되지 않는다. 그런 다음 내재된 긍정적인 피드백 때문에 눈사태와 같은 방식으로 전도성을 크게 증가시켜 콘덴서를 빠르게 방전시킨다. 캐패시터를 가로지르는 전압이 어느 정도 낮은 임계값 전압으로 떨어지면 장치는 실행을 중지하고 캐패시터는 다시 충전을 시작하고 주기는 ad infinitum을 반복한다.

임계값 요소가 네온 램프인 경우 회로는 캐패시터의 각 방전 시에도 섬광을 제공한다.^{[nb 1][nb 2]} 이 램프 예는 Pearson-Ason 효과를 설명하는 데 사용되는 일반적인 회로에 아래에 설명되어 있다. 방전 지속시간은 임계 요소에 직렬로 추가 저항을 연결함으로써 연장될 수 있다. 두 저항기는 전압 분할기를 형성하므로, 추가 저항기는 낮은 임계값에 도달할 수 있을 만큼 충분히 낮은 저항을 가져야 한다.

555 타이머로 대체 구현

위 네온 전구를 대신하는 555 타이머 IC(아스터블 모드에서 작동)로 유사한 이완 오실레이터를 만들 수 있다. 즉, 555 타이머 내에서 선택된 캐패시터를 설계 값(예: 전원 공급 전압의 2/3)으로 충전할 때 트랜지스터 스위치를 뒤집어서 선택한 저항기(RC 시간 상수)를 통해 점차적으로 콘덴서를 접지까지 방전시키는 것이다. 콘덴서가 충분히 낮은 값(예: 전원 공급 전압의 1/3)으로 떨어지는 순간 스위치가 뒤집혀 콘덴서가 다시 충전되도록 한다. 인기 있는 555의 대조군 설계는 5에서 15볼트 또는 더 넓은 범위에서 정확한 작동을 허용한다.

다른 비교기 오실레이터는 공급 전압이 변경될 경우 원치 않는 타이밍이 변경될 수 있다.

유도 발진기

펄스 변압기의 유도 특성을 이용하여 변압기를 포화상태로 유도하여 사각파를 생성하는 차단 오실레이터로, 변압기가 언로드되어 불포화될 때까지 변압기 공급전류를 차단하여 공급전류의 또 다른 펄스를 트리거하며, 일반적으로 단일 트랜지스터를 스위칭 일렉트로 사용한다.nt의

비교기 기반 이완 발진기

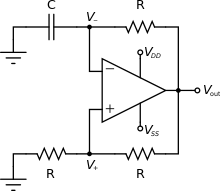
또는 캐패시터가 각 임계값에 도달하면 충전 소스를 양극 전원 공급기에서 음극 전원 공급기로 전환하거나 그 반대로 전환할 수 있다. 이 사례는 여기에서 비교기 기반 구현에 나타나 있다.

이 이완 오실레이터는 (작동 증폭기와 유사하게) 대조군과 함께 구현된 양성 피드백 루프에 의해 생성되는 이력 때문에 이 이름을 붙인 이력 오실레이터다. 이러한 형태의 이력 전환을 구현하는 회로를 Schmitt 트리거라고 한다. 방아쇠는 단독으로 바이스트 가능한 멀티비브레이터다. 그러나 RC 회로에 의해 트리거에 추가된 느린 음의 피드백은 회로가 자동으로 진동하도록 한다. 즉, RC 회로의 추가는 이력(hysteretic) 바이스트(bistable) 멀티비브레이터를 놀라운 멀티비브레이터로 바꾼다.

일반개념

대조군의 입력과 출력이 모두 0V일 경우 시스템은 불안정한 평형 상태에 있다. 열적 또는 전자기적 노이즈가 대조군의 출력을 0 이상으로 하는 순간(대조군 출력이 0 이하로 내려가는 경우 및 그에 따르는 것과 유사한 인수) 대조군의 양의 피드백은 양의 레일에 포화상태인 대조군의 출력을 초래한다.

즉, 현재 대조군의 출력이 양성이기 때문에 대조군에 대한 비파괴 입력도 양성이며, 전압분할기로 인해 출력이 증가함에 따라 계속 증가한다. 잠시 후 비교기의 출력은 양의 ${\displaystyle {전압}_{}}$ ${\displaystyle {\mathrm{레일}}_{}}$ V $D{\displaystyle {}_{}}$ ${\$이 된다$.$

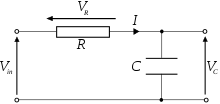
반전 입력과 비교기의 출력은 직렬 RC 회로에 의해 연결된다. 이 때문에 대조군의 반전 입력은 증상 없이 시간 상수 RC로 대조군 출력 전압에 접근한다. 반전 입력의 전압이 비반복 입력보다 큰 지점에서는 양의 피드백으로 인해 대조군의 출력이 빠르게 감소한다.

이는 비반복 입력이 변환 입력보다 적고 출력이 계속 감소할수록 입력 간 차이가 점점 더 음수화되기 때문이다. 다시, 반전 입력은 증상 없이 대조군의 출력 전압에 접근하며, 비반복 입력이 반전 입력보다 크면 사이클이 스스로 반복되므로 시스템이 진동한다.

예제: 대조약 기반 이완 오실레이터의 미분방정식 분석

${\$$V_{+}$는 ${\displaystyle V{}_{}}$ ${\displaystyle {o\mathrm{}}_{}}$ ${\displaystyle {\mathrm{u}}_{}}$ t ${\$에 의해 설정된다.저항성 전압 분할기의 $V_{\rm {out}}:$

${\displaystyle V_{+}={\frac {V_{\rm {out}}{2}}:}$

${\$$V_{-}$는 옴의 법칙과 캐패시터 차등식을 사용하여 얻는다$$.

${\displaystyle {\frac {V_{\rm {out}-V_{-}}{R}}=C{\frac {dV_}{dt}}}}$

${\displaystyle V{}_{}}$ -${\$$V_{-}$ 표준형식에 대한 미분방정식은$$ 다음과 같은 결과를 낳는다.

${\displaystyle {{dV_{-}}{dt}+{\frac {V_{-}}{RC}={\frac {V_{\rm {out}}}}{\frac}}}}{{dt}}}}}}{dt}}}}}}}}{{dt}}}}}}}}}}RC}}$

미분 방정식에 대한 두 가지 해결책, 즉 추진식 또는 특정 솔루션과 동질식 솔루션이 있다는 점에 주목하십시오. 추진 솔루션에 대해 해결하려면 이 특정 형태에 대해 솔루션이 일정한지 확인하십시오. ${\displaystyle 즉}$, ${\displaystyle V{}_{}}$-${\displaystyle {}_{}}$= A ${\displaystyle \,\!$$V_{-}=A}$ 여기서$$ A는 상수이고 ${\displaystyle \mathrm{d}}$ ${\displaystyle \frac{{}_{}}{\mathrm{-d}}}$ t${\displaystyle \frac{}{}}$= 0 ${\dplaystyle {\dV_}}{dt}=0}$.

${\displaystyle {\frac {A}{RC}}={\frac {V_{\rm {out}}{{out}}}{RC}}$

$\displaystyle \,\!A=V_{\rm {out}}$

라플라스 변환을 사용하여 동종 방정식 d ${\displaystyle \frac{{}_{}}{}}$- d ${\displaystyle \frac{t}{}}$+ V${\displaystyle \frac{{}_{}}{}}$- ${\displaystyle \frac{R}{}}$ ${\displaystyle \frac{{}_{}}{}}$= ${\displaystyle 0}$ ${\dplaystyle {\frac {dV_{-}-}+{dt}+{\frac$ {$V_{-}}{RC}=0}$을(를) 해결할 경우

${\displaystyle V_{-}=Be^{\frac{-1}{RC}t}}}$

${\$$V_{-}$는 특정 용액과 동질 용액의 합이다.

${\displaystyle V_{-}=A+Be^{\frac{-1}{RC}t}}}$

${\displaystyle V_{-}=V_{\rm {out}+Be^{\frac{-1}{RC}t}}$

B에 대한 해결은 초기 조건의 평가가 필요하다. 0시 $V{\displaystyle {}_{}}$ ${\displaystyle {o\mathrm{}}_{}}$ ${\displaystyle u_{}}$ ${\displaystyle {\mathrm{t}}_{}}$= ${\displaystyle V_{}}$ d ${\$ {$out},$ ${\displaystyle \mathrm{V<img\; alt="\{\backslash displaystyle\; V\_\{\backslash rm\; \{out\}\}=V\_\{dd\}\}"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/2889f3ab83abb3a823a460b0f0accd40d7c3d8af"\; style="vertical-align:\; -0.671ex;\; width:10.369ex;\; height:2.509ex;"\; papago-attr-id="273">}{}_{}}$-${\displaystyle {}_{}}$= 0 ${\displaystyle \,\!$$V_{-}=0$ 이전 방정식으로 대체하면

$\displaystyle \,\!0=V_{dd}+B}$

$\displaystyle \,\!B=-V_{dd}}$

진동 빈도

먼저 계산 용이성을 위해$$ $V{\displaystyle {}_{}}$ ${\displaystyle d_{}}$ ${\displaystyle d_{}}$=${\displaystyle }$- ${\displaystyle V_{}}$ s ${\$을(를) 가정해 보자. 주파수 계산과 무관한 캐패시터의 초기 충전을 무시한 채, 충전 및 $방전$은 ${\displaystyle \frac{V_{}}{}}$ d d ${\displaystyle \frac{d_{}}{}}$ d ${\displaystyle \frac{{}_{}}{\mathrm{}}}${\d displaystyle ${\frac{V_{ddd}:{2}}:$ $V$ ${\displaystyle \frac{s_{}}{}}$ ${\displaystyle \frac{{}_{}}{\mathrm{}}}$ ${\${\$frac{v_$}}{$ss}:{2$ 위의 회로의 경우 V가_ss 0 미만이어야 한다는 점에 유의하십시오. 기간(T)의 절반은 $V{\displaystyle {}_{}}$ ${\displaystyle {o\mathrm{}}_{}}$ ${\displaystyle {\mathrm{u}}_{}}$ ${\displaystyle {\mathrm{t}}_{}}$ ${\$이(가) V에서_dd 전환되는$$ 시간과 동일하다. V가₋ -${\displaystyle V\frac{{}_{}}{}}$ ${\displaystyle \frac{d_{}}{}}$ ${\displaystyle \frac{d_{}}{}}$ d ${\displaystyle \frac{{}_{}}{\mathrm{}}}$ 2$${\$displaystyle -{\frac {V_{dd}:{2}}:}$부터 ${\displaystyle \frac{V_{}}{}}$ d ${\displaystyle \frac{{}_{}}{\mathrm{}}}$ ${\displaystyle \frac{d_{}}{}}$ d 2 ${\$ {$V_{ddd}:{2}}:}$까지 충전될 때 이 문제가 발생한다$.$

${\displaystyle V_{-}=A+Be^{\frac{-1}{RC}t}}}$

${\displaystyle {\frac {V_{dd}{2}}=V_{dd}\좌측(1-{\{\frac {3}{2}}e^{\frac {-1}{RC}{\frac}{\frac {T}}}}오른쪽)}}}$

${\displaystyle {\frac{1}{3}}=e^{\frac {-1}{RC}{\frac {T}{2}}:$

${\displaystyle \ln \left({\frac {1}{3}\right)={\frac {-1}{RC}{\frac {T}{2}}:}$

$\displaystyle \,\!T=2\ln(3)RC}$

${\displaystyle \,\!f={\frac {1}{2\ln(3)RC}}$

V가_ss V의_dd 역이 아닐 때 우리는 비대칭 충전 및 방전 시간에 대해 걱정할 필요가 있다. 이 점을 고려했을 때, 우리는 결국 다음과 같은 형식의 공식으로 귀결된다.

${\displaystyle T=(RC)\left[\ln \ln \left({2V_{ss}-V_{ss}}\right)+\ln \left({\frac {2V_{ddd}-V_{ss}}}}}}}{v_{ss}\rig)\rig)\rig]}}}}$

이 ${\displaystyle {값}_{}}$은 ${\displaystyle V_{}}$d${\displaystyle {}_{}}$ = - ${\displaystyle V_{}}$s {\$dstyle V_{$dd$}=-V_${ss$}}}$인 경우 위의 결과로 감소한다$.$

참고 항목

• 멀티비브레이터
• FitzHugh-Nagumo 모델 – 예를 들어 뉴런의 이력 모델.
• Schmitt 트리거 – 비교기 기반 이완 오실레이터의 기반 회로.
• 유니작동 트랜지스터 – 진동을 완화할 수 있는 트랜지스터.
• Robert Kearns – 간헐적 와이퍼 특허 분쟁 시 이완 발진기를 사용.
• 한계 주기 – 이완 진동을 분석하는 데 사용되는 수학적 모델

메모들

참조

위키미디어 커먼스는 이완 오실레이터와 관련된 미디어를 보유하고 있다.