비선형 제어

피드백 제어 시스템.시스템(플랜트라고도 함)을 제어하여 출력이 원하는 기준 신호를 따르도록 하는 것이 좋습니다.센서는 출력을 감시하고 컨트롤러는 원하는 기준 출력에서 실제 출력을 감산하여 이 에러 신호를 시스템에 적용하여 출력을 기준치에 근접시킨다.비선형 제어 시스템에서 블록, 시스템, 센서 또는 컨트롤러 중 적어도 하나는 비선형이다.

비선형 제어 이론은 비선형, 시간 가변 또는 둘 다인 시스템을 다루는 제어 이론의 영역입니다.제어이론은 입력이 있는 동적 시스템의 동작과 피드백, 피드포워드 또는 신호 필터링을 사용하여 입력의 변화를 통해 출력을 수정하는 방법과 관련된 공학 및 수학 분야입니다.제어되는 시스템을 "플랜트"라고 합니다.시스템의 출력이 원하는 기준 신호를 따르도록 하는 한 가지 방법은 플랜트의 출력을 원하는 출력과 비교하여 원하는 출력에 근접하도록 출력을 수정하기 위한 피드백을 플랜트에 제공하는 것입니다.

제어이론은 두 갈래로 나뉜다.선형 제어 이론은 중첩 원리를 따르는 장치로 만들어진 시스템에 적용됩니다.이들은 선형 미분 방정식에 의해 제어됩니다.메이저 서브클래스는 LTI(Linear Time Universent) 시스템이라고 불리는 시간에 따라 변하지 않는 파라미터를 가진 시스템입니다.이러한 시스템은 라플라스 변환, 푸리에 변환, Z 변환, 보데 플롯, 루트 궤적 및 나이키스트 안정성 기준과 같은 매우 일반적인 강력한 주파수 영역 수학 기법으로 해결할 수 있습니다.

비선형 제어 이론은 중첩 원리를 따르지 않는 광범위한 종류의 시스템을 포함합니다.모든 실제 제어 시스템은 비선형이기 때문에 더 실제 시스템에 적용됩니다.이러한 시스템은 종종 비선형 미분 방정식의 지배를 받습니다.그것들을 다루기 위해 개발된 수학적 기법은 더 엄격하고 훨씬 덜 일반적이며, 종종 좁은 범주의 시스템에만 적용된다.여기에는 한계 주기 이론, 푸앵카레 지도, 리아푸노프 안정성 이론 및 기능 설명이 포함됩니다.안정점 근방의 해만이 관심 있는 경우에는 비선형 해법을 직렬로 확장하여 얻은 선형계로 근사함으로써 비선형계를 선형화한 후 선형 기술을 ^[1]사용할 수 있다.비선형 시스템은 시뮬레이션 언어를 사용하여 연산 시뮬레이션을 하는 등 컴퓨터에서 수치적 방법을 사용하여 종종 분석됩니다.설령 발전소가 선형이라 하더라도 비선형 제어기는 종종 더 어려운 설계 절차를 정당화하는 단순한 구현, 더 빠른 속도, 더 높은 정확성 또는 제어 에너지 감소와 같은 매력적인 기능을 가질 수 있다.

비선형 제어 시스템의 예는 서모스탯 제어 난방 시스템이다.용해로와 같은 건물 난방 시스템은 온도 변화에 대해 비선형 반응을 보입니다. 즉, "켜짐" 또는 "꺼짐" 상태이며 비례(선형) 장치가 가질 수 있는 온도 차이에 대한 미세 제어 기능이 없습니다.따라서 온도가 온도 조절기의 "켜짐" 설정값 아래로 떨어질 때까지 용해로는 꺼집니다.용해로의 열로 인해 온도가 상승하여 온도조절기의 "OFF" 설정점에 도달하여 용해로가 꺼지고 사이클이 반복됩니다.원하는 온도에 대한 이러한 온도 순환을 한계 주기라고 하며 비선형 제어 시스템의 특성입니다.

비선형 시스템의 특성

비선형 동적 시스템의 일부 특성은 다음과 같습니다.

중첩(선형성 및 균질성)의 원리를 따르지 않습니다.
이들은 복수의 고립된 평형점을 가질 수 있다.
한계 주기, 분기, 혼돈과 같은 특성을 나타낼 수 있습니다.
유한 이스케이프 시간:비선형 시스템의 솔루션이 항상 존재하는 것은 아닙니다.

비선형 시스템 분석 및 제어

비선형 피드백 시스템을 분석하기 위해 잘 개발된 몇 가지 기술이 있습니다.

기능 방법 설명
위상 평면법
랴푸노프 안정성 분석
특이 섭동법
절대 안정성에 대한 Popov 기준과 원 기준
중심 다양체 정리
소게인 정리
수동성 분석

비선형 시스템에 대한 제어 설계 기법도 존재합니다.이러한 기술은 각 영역에 대해 제한된 범위의 작동 및 사용(잘 알려진) 선형 설계 기법으로 시스템을 선형 시스템으로 취급하려는 기법으로 세분할 수 있습니다.

게인 스케줄링

제어 설계를 위해 시스템을 선형으로 취급할 수 있는 방식으로 보조 비선형 피드백을 도입하려는 사용자:

피드백 선형화

또한 Lyapunov 기반 방법:

비선형 피드백 분석 – Lur'e 문제

Lur'e 문제 블록 다이어그램

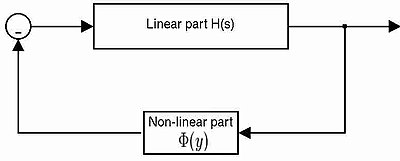
초기 비선형 피드백 시스템 분석 문제는 A. I. Lur'e에 의해 공식화되었습니다.Lur'e 문제로 기술된 제어 시스템은 선형적이고 시간 불변적인 전진 경로와 메모리 부족, 시간 가변성, 정적 비선형성을 포함하는 피드백 경로를 가집니다.

선형 부품은 4개의 매트릭스(A,B,C,D)로 특징지을 수 있으며, 비선형 부품은 ${\frac {\Phi (y)}{y}}\in [a,b],\quad a<b\quad \forall y$ ( ${\frac {\Phi (y)}{y}}\in [a,b],\quad a<b\quad \forall y$ y ${\frac {\Phi (y)}{y}}\in [a,b],\quad a<b\quad \forall y$ [ ${\frac {\Phi (y)}{y}}\in [a,b],\quad a<b\quad \forall y$ , b ${\frac {\Phi (y)}{y}}\in [a,b],\quad a<b\quad \forall y$ ], ${\frac {\Phi (y)}{y}}\in [a,b],\quad a<b\quad \forall y$ < b ${\frac {\Phi (y)}{y}}\in [a,b],\quad a<b\quad \forall y$ y \ $display$ style \ $frac$ \ $Phi ($ y ) { y } { y } \ $in [ a$ , $b$ ], $quad$ a \ $all$ \ all ( y )이다.

절대 안정성 문제

고려사항:

(A,B)는 제어 가능하고 (C,A)는 관측 가능
함수 δ의 섹터를 정의하는 2개의 실수 a, b(a < b)

Lur'e 문제(절대 안정성 문제로도 알려져 있음)는 전달 행렬 H(s)와 {a,b}만을 포함하는 조건을 도출하여 x = 0이 전체적으로 균등하게 점근적으로 안정된 시스템의 평형이다.

절대 안정성 문제에 대해 잘 알려진 두 가지 잘못된 추측이 있습니다.

이러한 추측은 그래픽적으로 δ(y) x y 그래프 또는 DΩ/dy x δ/^[2]y 그래프에 대한 그래픽 제한으로 해석할 수 있다.비선형성은 선형 안정성에 속하고 고유한 안정적인 균형은 안정적인 주기적 해인 숨겨진 진동과 공존한다는 아이저맨과 칼만의 추측에 반례가 있다.

절대 안정성에 대한 충분한 조건을 제공하는 루르 문제에 관한 두 가지 주요 이론이 있다.

원 기준(선형 시스템에 대한 나이키스트 안정성 기준의 확장)
Popov 기준.

비선형 제어의 이론적 결과

프로베니우스 정리

프로베니우스 정리는 미분 기하학의 깊은 결과이다.비선형 제어에 적용되었을 때 다음과 같이 표시됩니다.형태의 시스템이 주어졌을 경우

{dot {x}=\sum _{i=1}^{k}f_{i}(x)u_{i}(t),

$x\in R^{n}$ 서 x $x\in R^{n}$ $x\in R^{n}$ n $x\in R^{n}$ \ $displaystyle$ $x\in R^{n}$ x \ $in$ R^ { $n$ } , $f_{1},\dots ,f_{k}$ 1, $...$ , $f_{1},\dots ,f_{k}$ { $dots$ , $f$ _ { $k$ $}$ $u_{i}(t)$ $\Delta$ $display$ 、 $u_{i}(t)$ displaydisplaydisplaydisplaydisplay $displaydisplaydisplaydisplaydisplaydisplay$ $x$ $displaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplay$ displaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplay displaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplay displaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplay $displaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplay$ old of $dimension$ m $\operatorname {span} (\Delta )=m$ span $\operatorname {span} (\Delta )=m$ $\operatorname {span} (\Delta )=m$ $\operatorname {span} (\Delta )=m$ $=$ \ $displaystyle \operatorname {span}(\Delta$ ) = $m$ 및 $\operatorname {span} (\Delta )=m$ $\Delta$ \ $displaystyle \Delta }$ 의 $m$ $\Delta$ old는 involtional 분포입니다.

「」를 참조해 주세요.

레퍼런스

^ 트리밍 포인트
^ Naderi, T.; Materassi, D.; Innocenti, G.; Genesio, R. (2019). "Revisiting Kalman and Aizerman Conjectures via a Graphical Interpretation". IEEE Transactions on Automatic Control. 64 (2): 670–682. doi:10.1109/TAC.2018.2849597. ISSN 0018-9286.

추가 정보

Lur'e, A. I.; Postnikov, V. N. (1944). "К теории устойчивости регулируемых систем" [On the Theory of Stability of Control Systems]. Prikladnaya Matematika I Mekhanika (in Russian). 8 (3): 246–248.
Vidyasagar, M. (1993). Nonlinear Systems Analysis (2nd ed.). Englewood Cliffs: Prentice Hall. ISBN 978-0-13-623463-0.
Isidori, A. (1995). Nonlinear Control Systems (3rd ed.). Berlin: Springer. ISBN 978-3-540-19916-8.
Khalil, H. K. (2002). Nonlinear Systems (3rd ed.). Upper Saddle River: Prentice Hall. ISBN 978-0-13-067389-3.
Brogliato, B.; Lozano, R.; Maschke, B.; Egeland, O. (2020). Dissipative Systems Analysis and Control (3rd ed.). London: Springer.
Leonov G.A.; Kuznetsov N.V. (2011). "Algorithms for Searching for Hidden Oscillations in the Aizerman and Kalman Problems" (PDF). Doklady Mathematics. 84 (1): 475–481. doi:10.1134/S1064562411040120.
Bragin V.O.; Vagaitsev V.I.; Kuznetsov N.V.; Leonov G.A. (2011). "Algorithms for Finding Hidden Oscillations in Nonlinear Systems. The Aizerman and Kalman Conjectures and Chua's Circuits" (PDF). Journal of Computer and Systems Sciences International. 50 (5): 511–543. doi:10.1134/S106423071104006X.
Leonov G.A., Kuznetsov N.V. (2011). Sergio, Bittanti (ed.). "Analytical-numerical methods for investigation of hidden oscillations in nonlinear control systems" (PDF). IFAC Proceedings Volumes (IFAC-PapersOnline). Proceedings of the 18th IFAC World Congress. 18 (1): 2494–2505. doi:10.3182/20110828-6-IT-1002.03315. ISBN 9783902661937.

외부 링크

비선형 제어 시스템을 위한 울프람 언어 함수

[1] 트리밍 포인트

[2] Naderi, T.; Materassi, D.; Innocenti, G.; Genesio, R. (2019). "Revisiting Kalman and Aizerman Conjectures via a Graphical Interpretation". IEEE Transactions on Automatic Control. 64 (2): 670–682. doi:10.1109/TAC.2018.2849597. ISSN 0018-9286.

[1]

[2]

Search

비선형 제어

네임스페이스

더

목차

비선형 시스템의 특성

비선형 시스템 분석 및 제어

비선형 피드백 분석 – Lur'e 문제

절대 안정성 문제

비선형 제어의 이론적 결과

프로베니우스 정리

「」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

Search

비선형 제어

비선형 시스템의 특성

비선형 시스템 분석 및 제어

비선형 피드백 분석 – Lur'e 문제

절대 안정성 문제

비선형 제어의 이론적 결과

프로베니우스 정리

「 」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

「」를 참조해 주세요.