턴(각도)
Turn (angle)| 돌다 | |
|---|---|
 완전한 회전이 1회전의 회전 각도에 해당하는 중심점을 중심으로 반시계 방향으로 회전합니다. | |
| 일반정보 | |
| 단위 | 평면각 |
| 기호. | tr, pla, rev, cyc |
| 변환 | |
| 1 트레인... | ... ...와 맞먹습니다. |
| 라디안 | π 래드 2개 ≈ 6.283185307... rad |
| 밀리라디안 | 2000년 π mrad ≈ 6283.185307... 마드 |
| 도 | 360° |
| 그라디언스 | 400g |
원턴(기호 또는 평면 N)은 2개의 π 라디안, 360도 또는 400도 그라디언스와 동일한 평면 각도 측정 단위입니다. 따라서 그것의 중심에 있는 완전한 원으로 표시되는 각도 척도입니다. 각도 단위로서, 하나의 회전은 또한 하나의 주기(기호 순환 또는 c)[1] 또는 하나의 회전(기호 회전)에 해당합니다.[2] 주파수의 일반적인 관련 단위는 초당 사이클(cycle per second) 및 분당 회전(rpm)입니다.[a] 턴의 각도 단위는 무엇보다도 전자기 코일(예를 들어, 변압기), 회전하는 물체 및 곡선의 감김 수와 관련하여 유용합니다.
ISQ에서 임의의 "회전 수"("회전 수" 또는 "사이클 수"라고도 함)는 주어진 각도와 전체 회전의 비율로 정의되는 회전이라고 하는 무차원 양으로 공식화됩니다. 기호 N으로 표시됩니다. 회전의 세분화에는 각각 반원 및 직각에 걸쳐 있는 반회전 및 분기회전이 포함되며, 미터법 접두사는 예를 들어 센티턴(ctr), 밀리턴(mtr) 등에서 사용할 수도 있습니다.
각도를 나타내는 또 다른 일반적인 단위는 일반적으로πpi}(파이)로 표시되는 라디안입니다. 기호π\pi}는 한 번의 반회전을 나타내는 것으로 1706년 윌리엄 존스에 의해 개발된 후 레온하르트 오일러에 의해 대중화되었습니다. 2010년에 Michael Hartl은 개념적 단순성을 높이기 위해 기호τ tau}(tau)를 2개의 π 2\pi}와 하고 한 턴에 해당하는 τ를 사용할 것을 제안했습니다. 이 제안은 처음에 수학계에서 널리 받아들여진 것은 [6]아니지만 상수는 몇 가지 주요 프로그래밍 언어와 계산기에 추가되어 [7]더 널리 퍼졌습니다.
단위 기호
ISQ 및 SI 단위의 "N"
| 로테이션 | |
|---|---|
기타명 | 회전수, 회전수, 회전수, 회전수 |
공통 기호 | N |
| SI단위 | 유니트리스 |
| 치수 | 1 |
각도 단위 "턴(turn)"과 관련된 개념으로, ISQ(International System of Quantities)에 의해 정의되고 SI(International System of Unit)에 채택된 개념은 회전수로 정의되는 물리량 회전(symbol N)입니다.[8]
N은 예를 들어 주어진 축을 중심으로 회전하는 물체의 회전수(반드시 정수는 아님)입니다. 그 값은 다음과 같습니다.
- N=φ/π 래드 2개
여기서 φ은 회전 변위의 측정값을 나타냅니다.
상기 정의는 국제표준 ISO 80000-3(공간과 시간)에 공식화되어 [8]국제단위계(SI)에 채택된 국제수량계(ISQ)의 일부입니다.[9][10] ISQ/SI에서 회전은 SI 기본 단위가 역수 초(s)인 회전 주파수 n=dN/dt를 도출하는 데 사용되며, 주파수의 일반적인 관련 단위는 헤르츠(Hz), 초당 사이클(cps) 및 분당 회전(rpm)입니다.
| 레볼루션 | |
|---|---|
| 단위 | 로테이션 |
| 기호. | rev, r, cyc, c |
| 변환 | |
| ...에서 1회전. | ... ...와 맞먹습니다. |
| 기초단위 | 1 |
대체 버전인 ISO 80000-3:2006은 "혁명"을 무차원 단위 "one"의 특별한 이름으로 정의했으며,[b] 라디안과 같은 다른 특별한 이름도 받았습니다.[c] 차원의 동질성에도 불구하고 특별히 명명된 이 두 무차원 단위는 각각 회전과 각도라는 비교할 수 없는 종류의 양에 적용할 수 있습니다.[12] "Cycle"은 ISO 80000-3에서도 기간의 정의로 언급되어 있습니다.[d]
EU와 스위스의 "pla"
독일 표준 DIN 1315(1974년 3월)는 회전을 위한 단위 기호 "pla"(라틴어: plenus angulus 'full angle')를 제안했습니다.[13][14] DIN 1301-1[2010년 10월)에서 다루는 소위 볼윈켈('전각')은 SI 단위가 아닙니다. 그러나 EU와[15][16] 스위스의 법적 측정 단위입니다.[17]
계산기의 "tr"
과학 계산기 HP 39gII와 HP Prime은 각각 2011년과 2013년 이후의 턴에 대해 단위 기호 "tr"을 지원합니다. 2016년 HP 50g, 2017년 HP 39g+, HP 49g+, HP 39gs, HP 40gs에 대한 신규 RPL에도 "tr"에 대한 지원이 추가되었습니다.[18][19] 각도 모드 TURN WP 43S에 대해서도 제안되었지만, 계산기는 2019년 이후 모드와 단위로 "MUL π"(π의 배수)을 구현합니다.
2개의 π를 나타내는 한 글자에 대한 제안
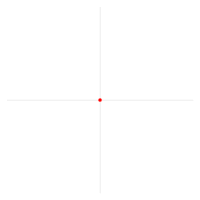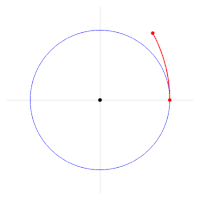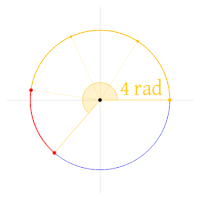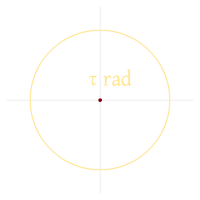
기호π\pi}의 의미는 원래 원주와 직경의 비율로 고정되지 않았습니다. 1697년, 데이비드 그레고리는 원의 둘레를 반지름으로 나눈 π/ρ(pi over rho)를 사용했습니다. 그러나 1647년 초 윌리엄 오어레드는 지름과 둘레의 비율을 위해 δ/π(델타 over pi)을 사용했습니다. 현재의 의미를 지닌 π 기호가 처음 사용된 것은 1706년 웨일스의 수학자 윌리엄 존스(William Jones)에 의해서였습니다. 그런 다음 오일러는 그런 의미를 가진 기호를 채택하여 널리 사용하게 되었습니다.[3]
2001년 로버트 팔레는 수학을 좀 더 쉽고 직관적으로 만들기 위해 반 바퀴를 돌 때의 라디안 수에 해당하는 π 대신 차례로 도는 라디안 수를 기본 원 상수로 사용할 것을 제안했습니다. 그의 제안은 를 나타내기 위해 "다리가 세 개인 π" 기호를 사용했습니다(π π = 2 π displaystyle \pi \!\;\!\!\!)! 2}).
2008년 토마스 콜리냐투스(Thomas Colignatus)는 2개의 π를 나타내는 대문자 그리스 문자 세타(theta)인 θ(THEAS)를 제안했습니다. 그리스 문자 세타는 페니키아어와 히브리어 문자인 테스, 𐤈 또는 ט에서 유래했으며, 바퀴를 의미하는 이전 버전의 상징은 4개의 바퀴가 달린 바퀴를 닮았다는 것이 관찰되었습니다. 또한 2 π 값을 나타내기 위해 바퀴 기호인 teth를 사용하는 것이 제안되었으며, 최근에는 바퀴, 태양, 원 또는 디스크 기호, 즉 teth의 다른 변형이 2 π 값을 나타내기 위해 존재하는 고대 문화권 사이에서 연결되었습니다.
2010년 마이클 하틀(Michael Hartl)은 그리스 문자 타우(tau)를 원 상수인 τ = 2 π를 나타내기 위해 사용할 것을 제안했습니다. 그는 두 가지 이유를 제시했습니다. 첫째, τ는 한 턴의 라디안 수이며, 이는 한 턴의 분수를 보다 직접적으로 표현할 수 있도록 합니다. 예를 들어, 3/4 턴은 3 π/2 rad 대신 3 τ/4 rad로 표현됩니다. 둘째, τ은 원 상수와의 연관성이 필연적인 π과 시각적으로 닮았습니다. 하틀의 타우 매니페스토는 π 대신 τ이 사용되는 곳이 더 명확하다고 주장되는 공식의 많은 예를 제공합니다. 예를 들어 e = -1 대신 e = 1을 사용하여 오일러의 동일성 기하학과 더 밀접한 연관성을 나타냅니다.
처음에는 이 두 제안 모두 수학계와 과학계에서 널리 받아들여졌습니다.[6] 그러나 τ의 사용은 다음과 같이 더 널리 퍼졌습니다.
- 2012년, 교육 웹사이트 칸 아카데미는 τ의 관점에서 표현된 답을 받아들이기 시작했습니다.
- The constant τ is made available in the Google calculator, Desmos graphing calculator[35] and in several programming languages such as Python,[36][37] Raku,[38] Processing,[39] Nim,[40] Rust,[41] GDScript,[42] UE Blueprints,[43] Java,[44][45] and .NET.[46][47]
- 또한 τ 촉진자인 피터 해레모 ë가 저술한 적어도 하나의 수학 연구 논문에도 사용되었습니다.
다음 표는 π 대신 τ = 2 π를 사용한 경우 다양한 ID가 어떻게 나타나는지 보여줍니다. 더 자세한 목록은 π을 포함하는 공식 목록을 참조하십시오.
| 공식 | π 사용 | τ 사용 | 메모들 |
|---|---|---|---|
| 원의 1/4로 표시된 각도 | π/2rad | τ/4rad | τ/4 rad = 1/4 turn |
| 반지름 r인 원의 원둘레 C | C = 2 πr | C = τ r | |
| 원의 넓이 | A = π r | A = 1/2 τ r | 각도 θ 섹터의 면적은 A = 1/2 θ r입니다. |
| 단위 둘레 반경을 갖는 정n각형의 넓이 | A = n/2 sin 2π/n | A = n/2 sin τ/n | |
| n-ball과 n-sphere 부피 반복 관계 | V(r) = r/n S(r) S(r) = 2 πr V(r) | V(r) = r/n S(r) S(r) = τ r V(r) | V(r) = 1 S(r) = 2 |
| 코시 적분식 | |||
| 표준정규분포 | |||
| 스털링 근사 | |||
| 오일러 항등식 | e = -1 e + 1 = 0 | e = 1 e - 1 = 0 | 임의의 정수 k에 대하여, e = 1 |
| 단결의 제n근 | |||
| 플랑크 상수 | ħ은 감소된 플랑크 상수입니다. | ||
| 각진동수 |
소분
턴은 100 센티미터 또는 1000 밀리 턴으로 나눌 수 있으며, 각 밀리 턴은 0.36°의 각도에 해당하며, 이는 21' 36 ″로 기록될 수도 있습니다. 회전수를 센티미터로 나눈 각도기를 일반적으로 "프로트랙터"라고 합니다.
퍼센트 각도기는 1922년부터 존재해 왔지만,[53] 센티턴, 밀리턴, 마이크로턴이라는 용어는 1962년 영국 천문학자 프레드 호일에 의해 훨씬 나중에 소개되었습니다.[51][52] 포병 및 위성 감시를 위한 일부 측정 장치는 밀리턴 스케일을 운반합니다.[54][55]
회전의 이진 분수도 사용됩니다. 선원들은 전통적으로 회전을 32개의 나침반 지점으로 나누었는데, 이 지점들은 암시적으로 1/32 회전의 각도 간격을 갖습니다. 이진 라디안(또는 브래드)이라고도 하는 이진도는 1/256 회전입니다.[56] 이진도는 각도가 단일 바이트에서 가능한 최대 정밀도로 표현될 수 있도록 컴퓨팅에 사용됩니다. 컴퓨팅에 사용되는 각도의 다른 측도는 하나의 전체 턴을 n의 다른 값에 대해 2등분하는n 것에 기초할 수 있습니다.[57]
단위전환


1회전은 2개의 π(≈ 6.283185307179586) 라디안, 360도 또는 400도 그라디언스와 같습니다.
| 턴즈 | 라디안 | 도 | 그라디언스 | |
|---|---|---|---|---|
| 0회전 | 0 rad | 0° | 0g | |
| 1/72턴 | 𝜏/72rad | π/36rad | 5° | 5+5/9g |
| 1/24턴 | 𝜏/24rad | π/12rad | 15° | 16+2/3g |
| 1/16 턴 | 𝜏/16rad | π/8rad | 22.5° | 25g |
| 1/12턴 | 𝜏/12rad | π/6rad | 30° | 33+1/3g |
| 1/10 턴 | 𝜏/10rad | π/5rad | 36° | 40g |
| 1/8턴 | 𝜏/8rad | π/4rad | 45° | 50g |
| 1/2 π 턴 | 1 rad | c. 57.3° | c. 63.7g | |
| 1/6턴 | 𝜏/6rad | π/3rad | 60° | 66+2/3g |
| 1/5회전 | 𝜏/5rad | 2π/5rad | 72° | 80g |
| 1/4회전 | 𝜏/4rad | π/2rad | 90° | 100g |
| 1/3회전 | 𝜏/3rad | 2π/3rad | 120° | 133+1/3g |
| 2/5회전 | 2𝜏/5rad | 4π/5rad | 144° | 160g |
| 1/2회전 | 𝜏/2rad | π 래드 | 180° | 200g |
| 4분의 3회전 | 3𝜏/4rad | 3π/2rad | 270° | 300g |
| 1회전 | 𝜏 래드 | π 래드 2개 | 360° | 400g |
참고 항목
- 암페어턴
- 헤르츠(현대식) 또는 초당 주기(구형)
- 회전각
- 분당 회전수
- 반복원
- Spat(각 단위) – 회전의 입체각 대응물로, 4개의 π 스테라디안에 해당합니다.
- 단위간격
- 신의 비율: 합리적인 삼각법과 보편기하학
- 모듈로 연산
- 트위스트(수학)
메모들
참고문헌
- ^ Fitzpatrick, Richard (2021). Newtonian Dynamics: An Introduction. CRC Press. p. 116. ISBN 978-1-000-50953-3. Retrieved 2023-04-25.
- ^ Units & Symbols for Electrical & Electronic Engineers (PDF). London, UK: Institution of Engineering and Technology. 2016. Archived (PDF) from the original on 2023-07-18. Retrieved 2023-07-18. (1+iii+32+1페이지)
- ^ a b "Pi". Encyclopaedia Brittanica. 2024-03-14. Retrieved 2024-03-26.
- ^ Euler, Leonhard (1746). Nova theoria lucis et colorum. Opuscula varii argumenti (in Latin). p. 200.
unde constat punctum B per datum tantum spatium de loco fuo naturali depelli, ad quam maximam distantiam pertinget, elapso tempore t=π/m denotante π angulum 180°, quo fit cos(mt)=- 1 & B b=2α.
[from which it is clear that the point B is pushed by a given distance from its natural position, and it will reach the maximum distance after the elapsed time t=π/m, π denoting an angle of 180°, which becomes cos(mt)=- 1 & B b=2α.] - ^ a b Hartl, Michael (2019-03-14) [2010-03-14]. "The Tau Manifesto". Archived from the original on 2019-06-28. Retrieved 2013-09-14.
- ^ a b "Life of pi in no danger – Experts cold-shoulder campaign to replace with tau". Telegraph India. 2011-06-30. Archived from the original on 2013-07-13. Retrieved 2019-08-05.
- ^ a b McMillan, Robert (2020-03-13). "For Math Fans, Nothing Can Spoil Pi Day—Except Maybe Tau Day". Wall Street Journal. ISSN 0099-9660. Retrieved 2020-05-21.
- ^ a b c [1]"ISO 80000-3:2019 Quantities and units — Part 3: Space and time" (2 ed.). International Organization for Standardization. 2019. Retrieved 2019-10-23. (11페이지)
- ^ Le Système international d’unités [The International System of Units] (PDF) (in French and English) (9th ed.), International Bureau of Weights and Measures, 2019, ISBN 978-92-822-2272-0
- ^ Thompson, Ambler; Taylor, Barry N. (2020-03-04) [2009-07-02]. "The NIST Guide for the Use of the International System of Units, Special Publication 811" (2008 ed.). National Institute of Standards and Technology. Retrieved 2023-07-17. [2]
- ^ a b "ISO 80000-3:2006". ISO. 2001-08-31. Retrieved 2023-04-25.
- ^ "ISO 80000-1:2009(en) Quantities and units — Part 1: General". iso.org. Retrieved 2023-05-12.
- ^ German, Sigmar; Drath, Peter (2013-03-13) [1979]. Handbuch SI-Einheiten: Definition, Realisierung, Bewahrung und Weitergabe der SI-Einheiten, Grundlagen der Präzisionsmeßtechnik (in German) (1 ed.). Friedrich Vieweg & Sohn Verlagsgesellschaft mbH, reprint: Springer-Verlag. p. 421. ISBN 978-3-32283606-9. 978-3-528-08441-7, 978-3-32283606-9. Retrieved 2015-08-14.
- ^ Kurzweil, Peter (2013-03-09) [1999]. Das Vieweg Einheiten-Lexikon: Formeln und Begriffe aus Physik, Chemie und Technik (in German) (1 ed.). Vieweg, reprint: Springer-Verlag. p. 403. doi:10.1007/978-3-322-92920-4. ISBN 978-3-32292920-4. 978-3-322-92921-1. Retrieved 2015-08-14.
- ^ "Richtlinie 80/181/EWG - Richtlinie des Rates vom 20. Dezember 1979 zur Angleichung der Rechtsvorschriften der Mitgliedstaaten über die Einheiten im Meßwesen und zur Aufhebung der Richtlinie 71/354/EWG" (in German). 1980-02-15. Archived from the original on 2019-06-22. Retrieved 2019-08-06.
- ^ "Richtlinie 2009/3/EG des Europäischen Parlaments und des Rates vom 11. März 2009 zur Änderung der Richtlinie 80/181/EWG des Rates zur Angleichung der Rechtsvorschriften der Mitgliedstaaten über die Einheiten im Messwesen (Text von Bedeutung für den EWR)" (in German). 2009-03-11. Archived from the original on 2019-08-06. Retrieved 2019-08-06.
- ^ "Art. 15 Einheiten in Form von nichtdezimalen Vielfachen oder Teilen von SI-Einheiten". Einheitenverordnung (in Swiss High German). Schweizerischer Bundesrat. 1994-11-23. 941.202. Archived from the original on 2019-05-10. Retrieved 2013-01-01.
{{cite book}}:work=무시됨(도움말) - ^ Lapilli, Claudio Daniel (2016-05-11). "RE: newRPL: Handling of units". HP Museum. Archived from the original on 2017-08-10. Retrieved 2019-08-05.
- ^ Lapilli, Claudio Daniel (2018-10-25). "Chapter 3: Units - Available Units - Angles". newRPL User Manual. Archived from the original on 2019-08-06. Retrieved 2019-08-07.
{{cite book}}:work=무시됨(도움말) - ^ Paul, Matthias R. (2016-01-12) [2016-01-11]. "RE: WP-32S in 2016?". HP Museum. Archived from the original on 2019-08-05. Retrieved 2019-08-05.
[…] I'd like to see a TURN mode being implemented as well. TURN mode works exactly like DEG, RAD and GRAD (including having a full set of angle unit conversion functions like on the WP 34S), except for that a full circle doesn't equal 360 degree, 6.2831... rad or 400 gon, but 1 turn. (I […] found it to be really convenient in engineering/programming, where you often have to convert to/from other unit representations […] But I think it can also be useful for educational purposes. […]) Having the angle of a full circle normalized to 1 allows for easier conversions to/from a whole bunch of other angle units […]
- ^ [3]Bonin, Walter (2019) [2015]. WP 43S Owner's Manual (PDF). 0.12 (draft ed.). pp. 72, 118–119, 311. ISBN 978-1-72950098-9. Archived (PDF) from the original on 2023-07-18. Retrieved 2019-08-05. [4] (314페이지)
- ^ [5]Bonin, Walter (2019) [2015]. WP 43S Reference Manual (PDF). 0.12 (draft ed.). pp. iii, 54, 97, 128, 144, 193, 195. ISBN 978-1-72950106-1. Archived (PDF) from the original on 2023-07-18. Retrieved 2019-08-05. [6] (271페이지)
- ^ Beckmann, Petr (1989) [1970]. A History of Pi. Barnes & Noble Publishing.
- ^ Schwartzman, Steven (1994). The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English. The Mathematical Association of America. p. 165. ISBN 978-0-88385511-9.
- ^ Veling, Anne (2001). "Pi through the ages". veling.nl. Archived from the original on 2009-07-02.
- ^ a b Palais, Robert (2001). "Pi is Wrong" (PDF). The Mathematical Intelligencer. 23 (3). New York, USA: Springer-Verlag: 7–8. doi:10.1007/bf03026846. S2CID 120965049. Archived (PDF) from the original on 2019-07-18. Retrieved 2019-08-05.
- ^ Cool, Thomas "Colignatus" (2008-07-18) [2008-04-08, 2008-05-06]. "Trig rerigged. Trigonometry reconsidered. Measuring angles in 'unit meter around' and using the unit radius functions Xur and Yur" (PDF). Archived from the original (PDF) on 2023-07-18. Retrieved 2023-07-18. (18페이지)
- ^ Mann, Steve; Janzen, Ryan E.; Ali, Mir Adnan; Scourboutakos, Pete; Guleria, Nitin (22–24 October 2014). "Integral Kinematics (Time-Integrals of Distance, Energy, etc.) and Integral Kinesiology". Proceedings of the 2014 IEEE GEM. Toronto, Ontario, Canada: 627–629. S2CID 6462220. Retrieved 2023-07-18.
- ^ Mann, Steve; Chen, Hongyu; Aylward, Graeme; Jorritsma, Megan; Mann, Christina; Defaz Poveda, Diego David; Pierce, Cayden; Lam, Derek; Stairs, Jeremy; Hermandez, Jesse; Li, Qiushi; Xiang, Yi Xin; Kanaan, Georges (June 2019). "Eye Itself as a Camera: Sensors, Integrity, and Trust". The 5th ACM Workshop on Wearable Systems and Applications (Keynote): 1–2. doi:10.1145/3325424.3330210. S2CID 189926593. Retrieved 2023-07-18.
- ^ Hartl, Michael (2010-03-14). "The Tau Manifesto" (PDF). Archived (PDF) from the original on 2019-07-18. Retrieved 2019-08-05.
- ^ Aron, Jacob (2011-01-08). "Michael Hartl: It's time to kill off pi". New Scientist. Interview. 209 (2794): 23. Bibcode:2011NewSc.209...23A. doi:10.1016/S0262-4079(11)60036-5.
- ^ Landau, Elizabeth (2011-03-14). "On Pi Day, is 'pi' under attack?". cnn.com. CNN. Archived from the original on 2018-12-19. Retrieved 2019-08-05.
- ^ Bartholomew, Randyn Charles (2014-06-25). "Let's Use Tau--It's Easier Than Pi - A growing movement argues that killing pi would make mathematics simpler, easier and even more beautiful". Scientific American. Archived from the original on 2019-06-18. Retrieved 2015-03-20.
- ^ "Happy Tau Day!". blog.khanacademy.org. 2012-06-28. Archived from the original on 2023-07-18. Retrieved 2020-12-19.
- ^ "Supported Functions". help.desmos.com. Archived from the original on 2023-03-26. Retrieved 2023-03-21.
- ^ Coghlan, Nick (2017-02-25). "PEP 628 -- Add math.tau". Python.org. Archived from the original on 2019-07-22. Retrieved 2019-08-05.
- ^ "math — Mathematical functions". Python 3.7.0 documentation. Archived from the original on 2019-07-29. Retrieved 2019-08-05.
- ^ "Perl 6 terms". Archived from the original on 2019-07-22. Retrieved 2019-08-05.
- ^ "TAU". Processing. Archived from the original on 2019-07-22. Retrieved 2019-08-05.
- ^ "math". Nim. Archived from the original on 2019-07-22. Retrieved 2019-08-05.
- ^ "std::f64::consts::TAU - Rust". doc.rust-lang.org. Archived from the original on 2023-07-18. Retrieved 2020-10-09.
- ^ "Constants @GDScript - Godot Engine (stable) documentation in English". Godot Docs.
- ^ "Get TAU - Unreal Engine 5.2 Documentation". Unreal Engine Docs.
- ^ Darcy, Joe. "JDK-8283136: Add constant for tau to Math and StrictMath". bugs.openjdk.org.
- ^ "Math class". Java 19 documentation.
- ^ John-H-K. "Add Math.Tau Pull Request #37517 · dotnet/Runtime". GitHub.
- ^ "Math.Tau Field". .NET Reference Documentation.
- ^ Harremoës, Peter (2017). "Bounds on tail probabilities for negative binomial distributions". Kybernetika. 52 (6): 943–966. arXiv:1601.05179. doi:10.14736/kyb-2016-6-0943. S2CID 119126029.
- ^ Harremoës, Peter (2018-11-17). "Al-Kashi's constant τ" (PDF). Archived (PDF) from the original on 2019-07-22. Retrieved 2018-09-20.
- ^ Abbott, Stephen (April 2012). "My Conversion to Tauism" (PDF). Math Horizons. 19 (4): 34. doi:10.4169/mathhorizons.19.4.34. S2CID 126179022. Archived (PDF) from the original on 2013-09-28.
- ^ a b Hoyle, Fred (1962). Chandler, M. H. (ed.). Astronomy (1 ed.). London, UK: Macdonald & Co. (Publishers) Ltd. / Rathbone Books Limited. LCCN 62065943. OCLC 7419446. (320페이지)
- ^ a b Klein, Herbert Arthur (2012) [1988, 1974]. "Chapter 8: Keeping Track of Time". The Science of Measurement: A Historical Survey (The World of Measurements: Masterpieces, Mysteries and Muddles of Metrology). Dover Books on Mathematics (corrected reprint of original ed.). Dover Publications, Inc. / Courier Corporation (originally by Simon & Schuster, Inc.). p. 102. ISBN 978-0-48614497-9. LCCN 88-25858. Retrieved 2019-08-06. (736페이지)
- ^ Croxton, Frederick E. (1922). "A Percentage Protractor - Designed for Use in the Construction of Circle Charts or "Pie Diagrams"". Journal of the American Statistical Association. Short Note. 18 (137): 108–109. doi:10.1080/01621459.1922.10502455.
- ^ Schiffner, Friedrich (1965). Wähnl, Maria Emma [in German] (ed.). "Bestimmung von Satellitenbahnen". Astronomische Mitteilungen der Urania-Sternwarte Wien (in German). 8. Wien, Austria: Volksbildungshaus Wiener Urania.
- ^ Hayes, Eugene Nelson (1975) [1968]. Trackers of the Skies. History of the Smithsonian Satellite-tracking Program. Cambridge, Massachusetts, USA: Academic Press / Howard A. Doyle Publishing Company.
- ^ "ooPIC Programmer's Guide - Chapter 15: URCP". ooPIC Manual & Technical Specifications - ooPIC Compiler Ver 6.0. Savage Innovations, LLC. 2007 [1997]. Archived from the original on 2008-06-28. Retrieved 2019-08-05.
- ^ Hargreaves, Shawn [in Polish]. "Angles, integers, and modulo arithmetic". blogs.msdn.com. Archived from the original on 2019-06-30. Retrieved 2019-08-05.
- ^ 시퀀스 OEIS: A019692














