페르마의 직각 삼각형 정리

두 개의 직각 삼각형으로, 위쪽의 두 다리는 다리와 같고 아래쪽의 두 다리는 빗변입니다.

a^{2}

길이에

a^{2}

2

({

b^{2}

c^{2}

({

displaystyle b^{

2

}) 및

c^{2}

({

displaystyle c^{

2

c^{2}

}})는

d^{2}

d2

({

displaystyle

d^{2

의 공백으로 구분된 산술적 수열을 형성합니다. 4가지

길이

a

a

b

,

displaystyledisplaystyledyled

에는 모두 사용할 수 없습니다.

le

c

c

및

d\

displaystyle

d는

d

정수

입니다.

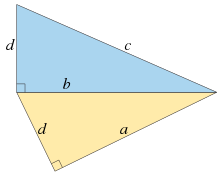
페르마의 직각 삼각형 정리는 수론에서 존재하지 않는 증거로, 피에르 드 페르마의 사망 직후인 1670년에 출판되었다.그것은 페르마에 ^[1]의해 주어진 유일한 완벽한 증거이다.그것은 여러 가지 동등한 제제를 가지고 있으며, 그 중 하나는 피보나치에 의해 1225년에 기술되었다(그러나 증명되지 않았다).기하학적 형태로 다음과 같이 기술되어 있습니다.

세 변의 길이가 모두 유리수인 유클리드 평면의 직각삼각형은 유리수의 제곱인 면적을 가질 수 없다.유리변 직각삼각형의 면적은 합동수라고 불리기 때문에 어떤 합동수도 제곱이 될 수 없다.
직각삼각형과 면적이 같은 정사각형은 모든 변이 서로 비례할 수는 없다.
한 삼각형의 두 다리가 다른 삼각형의 다리이자 빗변인 두 개의 정수변 직각 삼각형이 존재하지 않는다.

더 추상적으로, 디오판토스 방정식(다항식 방정식에 대한 정수 또는 유리수 해법)에 대한 결과로서, 다음과 같은 진술과 같다.

세 개의 정사각형 숫자가 산술 급수를 이루면, 연속된 수 사이의 간격은 정사각형일 수 없습니다.
$y^{2}=x(x-1)(x+1)$ $y^{2}=x(x-1)(x+1)$ 2 $=$ ( $y^{2}=x(x-1)(x+1)$ x - $y^{2}=x(x-1)(x+1)$ $x\in \{-1,0,1\}$ $y^{2}=x(x-1)(x+1)$ ) ( $y^{2}=x(x-1)(x+1)$ + $y^{2}=x(x-1)(x+1)$ ) ( x + 1 $y^{2}=x(x-1)(x+1)$ ) { $displaystyle$ y $^{2$ }= $x(x-1)(x+1)}$ (x $x\in \{-1,0,1\}$ { $x\in \{-1,0,1\}$ - $x\in \{-1,0,1\}$ 1 $x\in \{-1,0,1\}$ } { $displaystyle$ x $\in$ \ {-1 $,0,1\})$ $y=0$ y $y=0$ {\ $display style$ y= $y=0$ 0 . 0 $y=0$ 의 세 가지 사소한 점뿐입니다.
$x^{4}-y^{4}=z^{2}$ $x^{4}-y^{4}=z^{2}$ $x^{4}-y^{4}=z^{2}$ 4 - $x^{4}-y^{4}=z^{2}$ 4 $=$ $x^{4}-y^{4}=z^{2}$ 2 ({ $displaystyle$ x $^{4}-y^{4$ }= $z^{2})$ 는 $x^{4}-y^{4}=z^{2}$ 0이 아닌 정수해를 가지지 않는다.

이 공식들 중 마지막 공식의 직접적인 결과는 페르마의 마지막 정리가 그 지수가 4인 특별한 경우에 참이라는 것이다.

공식화

산술적 수열의 제곱

1225년, 프레데릭 2세 황제는 수학자 피보나찌에게 그의 궁정 철학자 팔레르모의 존이 세 가지 문제를 제기한 다른 수학자들과의 수학 대회에 참가하도록 도전했다. $이$ 문제들 중 첫 번째 문제에서는 정사각형이 5단위로 균등하게 떨어져 있는 3개의 유리수를 요구했는데, 피보나찌는 "Book of Squares"에서 ${\tfrac {31}{12}}$ ${\tfrac {41}{12}}$ ${\tfrac {31}{12}}$ ${\tfrac {41}{12}}$ ${\tfrac {49}{12}}$ ${\tfrac {41}{12}}$ ${\tfrac {49}{12}}$ 4912 ${\tfrac {49}{12}}$ 로 ${\tfrac {31}{12}}$ 했습니다.같은 해 후반 피보나치에 의해 출판된 그는 산술 급수를 형성하면서 서로 등간격인 제곱수의 3배를 찾는 보다 일반적인 문제를 풀었다.피보나찌는 이 숫자들 사이의 간격을 ^[2]합동이라고 불렀다.피보나찌의 해법을 설명하는 한 가지 방법은 제곱되는 숫자는 피타고라스 삼각형의 다리 차이, 빗변, 다리 합계가 되고, 합동은 같은 삼각형의 ^[3]4배라는 것이다.피보나찌는 합동이 제곱수라는 것 자체가 불가능하다고 관찰했지만, 이 ^[4]사실에 대한 만족스러운 증거는 제시하지 못했다.

3개의 $a^{2}$ $a^{2}$ 2 $({$ a $^{2$ $b^{2}$ ({ $displaystyle$ b $^{2$ $})$ $c^{2}$ $c^{2}$ 2 $({$ c $^{2$ 가 $c^{2}$ $d^{2}$ 인 산술적 수열을 형성할 수 있다면 이 숫자는 디오판틴 방정식을 만족시킬 수 있습니다.

{\displaystyle\signed}a^{2}+d^{2}}&=b^{2},\\b^{2}+d^{2}}&=c^{2}.\\\end {aligned}}

즉, 피타고라스의 정리에 따르면

(d,b)

그들은 쌍

(d,b)

(

,

b

)

({

displaystyle (d,

b

(d,b)

)})이 하나의 다리를 주고 작은 삼각형의 빗변과 같은 쌍이 큰 삼각형의 두 다리를 형성하는 두 개의 정수변 직각 삼각형을 형성할 것이다.그러나 (Fibonacci가 주장했듯이) 정사각형 합동이 존재할 수 없다면, 이러한 방식으로 ^[5]두 변을 공유하는 두 개의 정수 직각 삼각형이 존재할 수 없습니다.

직각 삼각형 영역

합동은 정확히 피타고라스 삼각형의 네 배 면적의 숫자이고, 4를 곱해도 숫자가 정사각형인지 아닌지는 변하지 않기 때문에, 정사각형 합동의 존재는 정사각형 면적을 가진 피타고라스 삼각형의 존재와 같다.페르마의 증거가 관련된 것은 이 문제의 변종이다: 그는 그러한 삼각형이 없다는 것을 보여준다.이 문제를 고려하면서 페르마는 피보나찌가 아니라 1621년 클로드 가스파르 바첼트 드 메지리악에 ^[6]의해 프랑스어로 번역된 디오판투스의 산술메티카 판에 의해 영감을 받았다.이 책은 정사각형과 관련된 형태의 영역을 가진 다양한 특수 직각삼각형에 대해 기술했지만 ^[7]정사각형 영역 자체의 경우는 고려하지 않았다.

위의 두 피타고라스 삼각형의 방정식을 다시 배열하고, 그것들을 곱하면, 단일 디오판토스 방정식을 얻을 수 있다.

\displaystyle b^{4}-d^{4}=(b^{2}-d^{2})(b^{2}+d^{2}=a^{2}c^{2}}

이는

e=ac

변수 e

=

\

displaystyle e=

ac를

e=ac

도입하여 단순화할 수 있습니다.

(\displaystyle b^{4}-d^{4}=e^{2}).}

반대로,

b^{4}-d^{4}=e^{2}

b

b^{4}-d^{4}=e^{2}

-

b^{4}-d^{4}=e^{2}

b^{4}-d^{4}=e^{2}

=

b^{4}-d^{4}=e^{2}

{\

displaystyle

b

^{4}-d^{

2}=

e^{2}}

에

b^{4}-d^{4}=e^{2}

따르는 3개의 양의 정수는 정사각형 합동으로 이어진다. 이 숫자들의 경우

(b^{4}-d^{4}-2b^{2}d^{2})^{2}

제곱수(

(b^{4}-d^{4}-2b^{2}d^{2})^{2}

-

(b^{4}-d^{4}-2b^{2}d^{2})^{2}

(b^{4}-d^{4}-2b^{2}d^{2})^{2}

-

(b^{4}-d^{4}-2b^{2}d^{2})^{2}

(b^{4}-d^{4}-2b^{2}d^{2})^{2}

(b^{4}-d^{4}-2b^{2}d^{2})^{2}

) 2 {\

displaystyle

(

b^4}-d^{2},{

2

2

}}^{2}}}^{{{{{}}}}}}}}}^2}^2}^2}^2}^2}^2}^2}^2}^2}^2}^

^{4}^{

2

(b^{4}+d^{4})^{2}

(b^{4}-d^{4}+2b^{2}d^{2})^{2}

및 (

(b^{4}-d^{4}+2b^{2}d^{2})^{2}

-

(b^{4}-d^{4}+2b^{2}d^{2})^{2}

4b^{2}d^{2}(b^{4}-d^{4})=(2bde)^{2}

+

(b^{4}-d^{4}+2b^{2}d^{2})^{2}

(b^{4}-d^{4}+2b^{2}d^{2})^{2}

4b^{2}d^{2}(b^{4}-d^{4})=(2bde)^{2}

)

(b^{4}-d^{4}+2b^{2}d^{2})^{2}

{{

4b^{2}d^{2}(b^{4}-d^{4})=(2bde)^{2}

(

4b^{2}d^{2}(b^{4}-d^{4})=(2bde)^{2}

^{4

4b^{2}d^{2}(b^{4}-d^{4})=(2bde)^{2}

^{2}^2

}^2

}^

2

(b^{4}-d^{4}+2b^{2}d^{2})^{2}

}

4b^{2}d^{2}(b^{4}-d^{4})=(2bde)^{2}

(

4b^{2}d^{2}(b^{4}-d^{4})=(2bde)^{2}

)

2 {

display

^2}

의 산술 급수를 형성한다.따라서,

b^{4}-d^{4}=e^{2}

b^{4}-d^{4}=e^{2}

- d

b^{4}-d^{4}=e^{2}

=

2 {\

displaystyle b^{4}-

d^{

4}=e^{2

}}의

b^{4}-d^{4}=e^{2}

용해도는 제곱합이 존재하는 것과 같다.단, 페르마의 마지막 정리에

x^{4}+y^{4}=z^{4}

+

x^{4}+y^{4}=z^{4}

x^{4}+y^{4}=z^{4}

의 정수해인

지수4

displaystyle 4

에 대한 반례가 있다면, 반례에서 세 개의

숫자

중 하나를 제곱하면

b^{4}-d^{4}=e^{2}

- 4

b^{4}-d^{4}=e^{2}

d

x^{4}+y^{4}=z^{4}

b^{4}-d^{4}=e^{2}

를

x^{4}+y^{4}=z^{4}

b^{4}-d^{4}=e^{2}

세 개의

b^{4}-d^{4}=e^{2}

가 나온다.\

displaystyle

b

^{4}-d^{4}=e^{

2

b^{4}-d^{4}=e^{2}

따라서 피타고라스 삼각형이 정사각형 면적을 가지지 않는다는 페르마의 증명은 페르마의 마지막 ^[7]정리의 지수

4(\

displaystyle

4

)

의 진상을 암시한다

.

같은 문제의 또 다른 등가 공식은 합동수, 즉 세 변이 모두 유리수인 직각 삼각형의 영역이다.변에 공통분모를 곱함으로써 어떤 합동수라도 피타고라스 삼각형의 영역으로 변환될 수 있으며, 여기서부터 합동수는 합수에 유리수의 ^[8]제곱을 곱함으로써 형성된 정확히 그 수이다.따라서, 제곱합이 존재한다는 것은 숫자 1이 합동수가 아니라는 ^[9]진술과 같다.이 공식을 표현하는 또 다른 기하학적 방법은 정사각형(기하학적 형상)과 직각삼각형은 동일한 면적과 모든 변이 서로 ^[10]비례하는 것을 가질 수 없다는 것이다.

타원 곡선

타원

곡선 2

y =

x (x

+ 1

)(x

- 1

)입니다.세 개의 유리점(-1,0), (0,0) 및 (1,0)은 이 곡선과 x축의 교차점입니다.

그러나 페르마 정리의 또 다른 등가 형식은 데카르트 좌표 $(x,y)$ ( $(x,y)$ , $(x,y)$ ) { $displaystyle ($ x $, y$ )}이 $(x,y)$ 방정식을 만족시키는 점들로 구성된 타원 곡선을 포함한다.

\displaystyle y^{2}=x(x+1)(x-1).}

점(-1,0), (0,0) 및 (1,0)은 이 방정식에 대한 명확한 해답을 제공합니다.페르마의 정리는 곡선에서

x

와

x

y

가

y

모두

x

인 유일한 점이라는 진술과 같다.보다 일반적으로 유리변과

면적

n {\

displaystyle

n

}

을

n

갖는 직각 삼각형은 타원

y^{2}=x(x+n)(x-n)

y

y^{2}=x(x+n)(x-n)

y^{2}=x(x+n)(x-n)

y^{2}=x(x+n)(x-n)

(

y^{2}=x(x+n)(x-n)

+

y^{2}=x(x+n)(x-n)

)

y^{2}=x(x+n)(x-n)

(

y^{2}=x(x+n)(x-n)

-

y^{2}=x(x+n)(x-n)

n ) \

display

y {2} =

y^{2}=x(x+n)(x-n)

x (

x

+

n

)

y^{2}=x(x+n)(x-n)

^[11]의 양의

y

- 좌표를

y

갖는 유리점과 1 대 1로 대응한다.

페르마의 증명

생전에 페르마는 정사각형 면적의 피타고라스 삼각형이 존재하지 않는다는 것을 증명하기 위해 몇몇 다른 수학자들에게 도전했지만, 그 증거를 직접 발표하지는 않았다.하지만, 그는 디오판토스의 산술학 사본에 페르마의 마지막 정리를 증명할 수 있다는 증거를 썼습니다.페르마의 아들 클레멘트 사무엘은 1670년 ^[12]직각 삼각형 정리의 증명과 함께 페르마의 한계 주해를 포함한 이 책의 판을 출판했다.

페르마의 증거는 무한 하강으로 인한 증거이다.그것은 정사각형 면적을 가진 피타고라스 삼각형의 어떤 예에서도 더 작은 예시를 도출할 수 있다는 것을 보여준다.피타고라스 삼각형은 양의 정수 영역을 가지고 있고 양의 정수의 무한 내림차순이 존재하지 않기 때문에, 정사각형 ^[13]면적을 가진 피타고라스 삼각형 또한 존재할 수 없습니다.

자세한 내용은 x $(\displaystyle$ x $x$ $(\displaystyle$ y $y$ $및$ z(\ $displaystyle$ z $)$ 가 $z$ 정사각형 면적의 직각 삼각형의 정수 변이라고 가정합니다.어떤 흔한 요인들로 나눔으로써, 누구도 이 삼각형은 모든 원시 피타배의 알려진 형태에서, 설정할 수 있primitive[10]것이다.)는 문제는=2pq{\displaystyle x=2pq}, 그건)p2− q2{\displaystyle y=p^{2}-q^{2}}, z)p2+q2{\displaystyle z=p^{2}+q^{2}}, 추정할 수 있다.tr $pq(p^{2}-q^{2})$ $pq(p^{2}-q^{2})$ 2 - $pq(p^{2}-q^{2})$ 2) $pq(p^{2}-q^{2})$ { $display pq(p^{2}-q^{2})$ 가 $pq(p^{2}-q^{2})$ 정사각형일 정도로 비교적 $소수인$ p $\$ $style$ $p$ \style p $\$ displaystyle q $p$ } $q$ 와 q\ $displaystyle$ q{2}(짝수 중 하나)를 찾는 데 사용된다.이 숫자가 정사각형이 되려면 $p+q=r^{2}$ 의 $선형$ $계수$ $p+q$ \ $displaystyle$ p $q$ $p+q$ q $\$ $displaystyle$ p $+$ $p-q$ $,$ $p-q$ - $p-q$ q \ $displaystyle p-q$ $p+q$ $p-q$ $p-q=s^{2}$ - $p-q=s^{2}$ q \ $displaystyle p-q\,$ p $p+q=r^{2}$ - $p+q=r^{2}$ $\$ $displaystyle$ $p-q\,$ p - $p-q=s^{2}$ 이어야 합니다. $p-q=s^{2}$ $p\$ $displaystyle$ $p$ 또는q\ $displaystyle$ q $p$ $q$ 중 $p$ 가 짝수이고 다른 하나가 홀수이므로 r $\displaystyle$ r과 $r$ $\displaystyle$ s는 $s$ $모두$ 홀수여야 합니다. $따라서$ r - $r-s$ \ displaystyle $r-s$ 와 $r-s$ $r+s$ + $r+s$ \ $displaystyle$ r $+s$ 는 $r+s$ $r-s$ 짝수이며, 둘 중 하나는 4로 나누어집니다.두 개로 나누면 두 개의 $u=(r-s)/2$ $u=(r-s)/2$ ( $u=(r-s)/2$ - $u=(r-s)/2$ s ) $u=(r-s)/2$ / $u=(r-s)/2$ { { $displaystyle$ u $u=(r-s)/2$ $v=(r+s)/2$ ( $v=(r+s)/2$ $u=(r-s)/2$ - s ) / $u=(r-s)/2$ $v=(r+s)/2$ { displaystyle v = $v=(r+s)/2$ ( $r$ + $v=(r+s)/2$ s ) / 2 { $displaystyle$ v $=$ ( r + s ) $v=(r+s)/2$ / $2가$ 더 생성되며, 그 중 하나는 앞의 문장으로도 마찬가지입니다. $u^{2}+v^{2}=(r^{2}+s^{2})/2=p$ 2 + $u^{2}+v^{2}=(r^{2}+s^{2})/2=p$ 2 $u^{2}+v^{2}=(r^{2}+s^{2})/2=p$ ( $u^{2}+v^{2}=(r^{2}+s^{2})/2=p$ 2 + $u^{2}+v^{2}=(r^{2}+s^{2})/2=p$ ) / $u^{2}+v^{2}=(r^{2}+s^{2})/2=p$ $u^{2}+v^{2}=(r^{2}+s^{2})/2=p$ { { \ $displaystyle u^$ ${2}$ + $v^ {$ 2} / 2 $uv/2=q/4$ p }는 $u^{2}+v^{2}=(r^{2}+s^{2})/2=p$ $u$ 이므로u { $displaystyle$ $}$ 및 $u$ $v$ { \ $displaystyle$ v $}$ 는 $v$ 면적 $uv/2=q/4$ / $2인$ $uv/2=q/4$ 원시 피타고라스 삼각형의 다리입니다 $.$ self square이고 $uv$ v{\ $displaystyle$ uv}는 $uv$ $uv$ 이므로 $q/4$ q / $q/4$ {\ $displaystyle q$ /4 $}$ 는 $q/4$ 정사각형입니다.따라서, 정사각형 면적을 가진 피타고라스 삼각형이 정사각형 면적을 가진 더 작은 피타고라스 삼각형으로 이어져 ^[14]증거를 완성합니다.

메모들

^ Edwards(2000).고트프리드 빌헬름 라이프니츠(1678), 레온하르트 오일러(1747), 베르나르 프레니클 드 베시(1765 이전)를 포함한 많은 후속 수학자들이 증거를 발표했다. 딕슨과 골드스타인(1995)을 참조하라.
^ 브래들리(2006년).
^ 베일러(1964년)
^ 광석(2012년);딕슨(1920).
^ 두 변을 공유하는 두 개의 직각삼각형이 있을 수 없다는 사실과 이 문제와 산술적 연속의 제곱 문제 사이의 연관성은 Cooper & Poirl(2008)에 의해 "잘 알려진" 것으로 기술되었다.
^ Edwards(2000).
^ ^a ^b 스틸웰(1998).
^ 콘래드(2008년 ), 코블리츠(1993년, 페이지 3).
^ 콘래드(2008), 정리 2; 코블리츠(1993), 연습 3, 페이지 5.
^ ^a ^b 딕슨(1920).
^ 코블리츠(1993), 발의안 19, 46~47페이지, 가토&사이토(2000).
^ Edwards(2000);딕슨(1920).기타 증거는 Grant & Perella(1999년)와 Barbara(2007년)를 참조한다.
^ Edwards(2000);딕슨(1920).
^ Edwards(2000);딕슨(1920년); 스틸웰(1998년).

레퍼런스

Barbara, Roy (July 2007), "91.33 Fermat's last theorem in the case $n=4$ ", Notes, The Mathematical Gazette, 91: 260–262, JSTOR 40378352
Beiler, Albert H. (1964), Recreations in the Theory of Numbers: The Queen of Mathematics Entertains, Dover Books, p. 153, ISBN 978-0-486-21096-4
Bradley, Michael John (2006), The Birth of Mathematics: Ancient Times to 1300, Infobase Publishing, p. 124, ISBN 978-0-8160-5423-7
Conrad, Keith (Fall 2008), "The congruent number problem" (PDF), Harvard College Mathematical Review, 2 (2): 58–73, archived from the original (PDF) on 2013-01-20
Cooper, Joshua; Poirel, Chris (2008), Pythagorean partition-regularity and ordered triple systems with the sum property, arXiv:0809.3478
Dickson, Leonard Eugene (1920), "Sum or difference of two biquadrates never a square; area of a rational right triangle never a square", History of the Theory of Numbers, Volume II: Diophantine Analysis, Carnegie Institution of Washington, pp. 615–620
Edwards, Harold M. (2000), "1.6 Fermat's one proof", Fermat's Last Theorem: A Genetic Introduction to Algebraic Number Theory, Graduate Texts in Mathematics, vol. 50, Springer, pp. 10–14, ISBN 978-0-387-95002-0
Goldstein, Catherine (1995), Un théorème de Fermat et ses lecteurs, Saint-Denis: Presses Universaires de Vincennes
Grant, Mike; Perella, Malcolm (July 1999), "83.25 Descending to the irrational", Notes, The Mathematical Gazette, 83: 263–267, doi:10.2307/3619054, JSTOR 3619054
Kato, Kazuya; Saitō, Takeshi (2000), Number Theory: Fermat's dream, Translations of mathematical monographs, translated by Nobushige Kurokawa, American Mathematical Society, p. 17, ISBN 978-0-8218-0863-4
Koblitz, Neal (1993), Introduction to Elliptic Curves and Modular Forms, Graduate Texts in Mathematics, vol. 97 (2nd ed.), Springer-Verlag, ISBN 0-387-97966-2
Ore, Øystein (2012), Number Theory and Its History, Dover Books, pp. 202–203, ISBN 978-0-486-13643-1
Stillwell, John (1998), "4.7 The area of rational right triangles", Numbers and Geometry, Undergraduate Texts in Mathematics, Springer, pp. 131–133, ISBN 978-0-387-98289-2

[1] Edwards(2000).고트프리드 빌헬름 라이프니츠(1678), 레온하르트 오일러(1747), 베르나르 프레니클 드 베시(1765 이전)를 포함한 많은 후속 수학자들이 증거를 발표했다. 딕슨과 골드스타인(1995)을 참조하라.

[FOOTNOTEBradley2006-2] 브래들리(2006년).

[FOOTNOTEBeiler1964-3] 베일러(1964년)

[4] 광석(2012년);딕슨(1920).

[5] 두 변을 공유하는 두 개의 직각삼각형이 있을 수 없다는 사실과 이 문제와 산술적 연속의 제곱 문제 사이의 연관성은 Cooper & Poirl(2008)에 의해 "잘 알려진" 것으로 기술되었다.

[FOOTNOTEEdwards2000-6] Edwards(2000).

[FOOTNOTEStillwell1998-7] 스틸웰(1998).

[8] 콘래드(2008년 ), 코블리츠(1993년, 페이지 3).

[9] 콘래드(2008), 정리 2; 코블리츠(1993), 연습 3, 페이지 5.

[FOOTNOTEDickson1920-10] 딕슨(1920).

[11] 코블리츠(1993), 발의안 19, 46~47페이지, 가토&사이토(2000).

[12] Edwards(2000);딕슨(1920).기타 증거는 Grant & Perella(1999년)와 Barbara(2007년)를 참조한다.

[13] Edwards(2000);딕슨(1920).

[14] Edwards(2000);딕슨(1920년); 스틸웰(1998년).

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

v t 피에르 드 페르마
일하다.	페르마의 마지막 정리 페르마 수 페르마의 원리 페르마의 소정리 페르마 다각형 수 정리 페르마 유사 프리미 페르마점 페르마의 정리(정지점) 두 제곱합에 대한 페르마의 정리 페르마의 나선 페르마의 직각 삼각형 정리
관련된	피에르 드 페르마의 이름을 딴 것 목록 와일스의 페르마의 마지막 정리 증명 페르마의 소설 속 마지막 정리 페르마상 페르마의 마지막 탱고(2000년 뮤지컬) 페르마의 마지막 정리 (인기과학서적)

Search