부가 백색 가우스 노이즈

이 기사는 대부분 또는 전체적으로 단일 출처에 의존하고 있습니다. 관련 토론은 토크 페이지에서 확인할 수 있습니다. 추가 출처에 인용문을 도입하여 이 기사의 개선에 도움을 주시기 바랍니다.출처 : '추가 화이트 가우스 노이즈'– 뉴스 · 신문 · 서적 · 학자 · JSTOR (2020년 2월)

부가 백색 가우스 노이즈(AWGN)는 정보 이론에서 자연에서 발생하는 많은 랜덤 프로세스의 효과를 모방하기 위해 사용되는 기본 노이즈 모델입니다.수식자는 특정 특성을 나타냅니다.

• 정보 시스템에 내재되어 있을 수 있는 모든 소음에 추가되기 때문에 가법입니다.
• 흰색은 정보 시스템의 주파수 대역 전체에 걸쳐 균일한 전력을 갖는다는 개념입니다.이는 가시 스펙트럼의 모든 주파수에서 균일한 방출을 갖는 흰색과 유사합니다.
• 가우스: 평균 시간 영역 값이 0인 시간 영역에 정규 분포를 가지기 때문입니다.

광대역 소음은 도체 내 원자의 열 진동(열 소음 또는 존슨-나이키스트 소음이라 함), 샷 소음, 지구 및 기타 따뜻한 물체로부터의 흑체 복사 및 태양과 같은 천체 소스에서 발생한다.확률론의 중심 한계 정리는 많은 무작위 과정의 합계가 가우스 또는 정규라고 불리는 분포를 갖는 경향이 있음을 나타냅니다.

AWGN은 종종 일정한 스펙트럼 밀도(대역폭 헤르츠당 와트로 표현됨)와 진폭의 가우스 분포를 가진 광대역 또는 백색 노이즈의 선형 추가가 유일한 통신 장애인 채널 모델로 사용됩니다.이 모델에서는 페이딩, 주파수 선택성, 간섭, 비선형성 또는 산포를 고려하지 않습니다.그러나, 그것은 이러한 다른 현상들을 고려하기 전에 시스템의 기본 동작에 대한 통찰력을 얻는 데 유용한 간단하고 다루기 쉬운 수학적 모델을 생산한다.

AWGN 채널은 많은 위성 및 심우주 통신 링크에 적합한 모델입니다.멀티패스, 지형블로킹, 간섭 등으로 인해 대부분의 지상파 링크에는 적합하지 않습니다.그러나, 지상 경로 모델링의 경우, AWGN은 일반적으로 연구 대상 채널의 배경 소음과 더불어, 최신 무선 시스템이 지상 운영에서 겪는 다중 경로, 지형 차단, 간섭, 지상 혼란 및 자기 간섭을 시뮬레이션하는 데 사용됩니다.

채널 용량

AWGN 채널은 이산 시간 이벤트 $색인{\displaystyle }$i에서$$일련의 출력 $Yi$(\displaystyle ${\displaystyle {Y\_}_{}}$${$$i$$\})$로 표시됩니다$.$ $Yi(\$displaystyle $Y_$${$$i$})는 $입력{\displaystyle {}_{}}$ $(\$와 ${\displaystyle {노이즈}_{}}$ $Zi$$(\$$$$Z_i$$})$의 합입니다.$분산{\displaystyle }$ N$($$N$)($잡음$)을 갖는 0-평균 정규 분포에서 도출된 종속적 분포입니다.$($ Z_${i$})는 $($ X_${i$와 상관관계가 없는 것으로 간주됩니다.

${\displaystyle Z_{i}\sim {\mathcal {N}}(0,N)\!}$

${\displaystyle Y_{i}=X_{i}+Z_{i},\!}$

$노이즈{\displaystyle }$N({$displaystyle$N})이$$ 0이 아니고 $({$})가 충분히 구속되지 않는 한 채널 용량은 무한합니다.입력에 대한 가장 일반적인 제약은 이른바 "전원" 제약으로, 채널을 통해 전송되는 코드워드$({\displaystyle {}_{}}$x 1, ${\displaystyle {x\mathrm{}}_{}}$2,${\displaystyle }$…,${\displaystyle {}_{}{x}_{}}$ k$$) {$displaystyle(x_{1$},$x_{2},\dots,x_{k})$에 대해 다음과 같은 조건을 충족해야 합니다.

${{displaystyle {1}{k}\sum _{i=1}^{k}x_{i}^2}^{2}\leq P,}$

$여기$서 P$(\displaystyle$ P$)$는 최대 채널 전력을 나타냅니다$$.따라서 전력 제한 채널의 채널 용량은 다음과 같이 계산됩니다.

${\displaystyle C=\max _{f(x){\text{s.t.}}E\left(X^{2}\오른쪽)\leq P}I(X;Y)\!}$

$여기$서 f$x)$ {{$displaystyle$$f($x)}는$$ X$(\displaystyle$X$)$의 분포입니다.I$X;Y)$ {displaystyle I(X$Y$를 전개하여 차분 엔트로피로 씁니다.

$디스플레이 스타일I(X;Y)=h(Y)-h(Y X)&=h(Y)-h(X+Z X)&=h(Y)-h(Z X)\end{aligned},\!}$

그러나 X$(디스플레이 스타일$ X$)$와 Z$(디스플레이 스타일$ Z$)$는 독립적입니다.

${\displaystyle I(X;Y)=h(Y)-h(Z)\!}$

가우스의 미분 엔트로피를 평가하면 다음과 같은 결과를 얻을 수 있습니다.

${\displaystyle h(Z)=syslogfrac {1}{2}}\log(2\pi eN)\!}$

$({displaystyle$X})와$$Z({$displaystyle$Z})는$$ 독립적이며 합계는 Y$({displaystyle$Y$\})$를 나타냅니다.

$\displaystyle E(Y^{2})=E(X+Z)^{2}=E(X^{2})+2E(Z)+E(Z^{2})\leq P+N,\!}$

이 한계로부터, 우리는 미분 엔트로피의 특성으로부터 다음과 같이 추론한다.

$\displaystyle h(Y)\leq {frac {1}{2}}\log(2\pi e(P+N)\!}$

따라서 채널 용량은 상호 정보에 대해 달성 가능한 가장 높은 한계로 지정됩니다.

${\displaystyle I(X;Y)\leq {frac {1}{2}}\log(2\pi e(P+N)}\log(2\pi eN)\!}$

$여기$서${\displaystyle }$I ( ${\displaystyle X}$;${\displaystyle Y}$) { $displaystyle$I ( $X$; Y )$$}는$$ 다음과 같은 경우에 최대화됩니다.

${\displaystyle X\sim {N}}(0,P),\!}$

따라서 AWGN 채널의 채널 $용량{\displaystyle }$C(\$displaystyle$ C$)$는 다음과 같습니다.

${\displaystyle C=black {1}{2}}\log \left(1+{\flac {P}{N}}\right},\!}$

채널 용량 및 구면 패킹

$(\displaystyle$1$$) ~ $(\displaystyle$ M$)$ 범위의 인덱스를 사용하여 채널을 통해 메시지를 전송한다고 가정합니다.$(\displaystyle$ M$)$ 메시지를$$ n$(\displaystyle$ n$)$ $비트로$ 인코딩하면 R$(\displaystyle$ R$)$ $레이트$를 다음과 같이 정의합니다.

${\displaystyle R=syslogfrac {n},\!}$

n${display style$ n$}$이 무한대에 가까워질 $때{\displaystyle }$ 오류의 최대 확률이 0이 되도록 코드 시퀀스가 있는 경우 이 속도는 달성 가능하다고 한다.$용량{\displaystyle }$C(\$displaystyle$ C$)$는 달성 가능한 최고 속도입니다.

$노이즈{\displaystyle }$ 레벨 N({$displaystyle$N$\})$의 AWGN 채널을 통해 송신된 $({displaystyle$n})의$$ 코드워드를 생각해 보겠습니다.이 코드워드를 수신하면 벡터 분산은 N$({displaystyle$N$\})$이 $되며{\displaystyle }$, 그 평균은 송신된 코드워드가 됩니다.벡터는 송신된 코드워드 $주위$의 ${\displaystyle \sqrt{\mathrm{반경n}(N}}$ +${\$ )(\$displaystyle${n$(N+\epsilon)})$ 구에$$ 포함되어 있을 가능성이 매우 높습니다.수신된 모든 메시지를 이 구면의 중심에 있는 코드워드에 매핑하여 디코딩하면 수신된 벡터가 이 구 밖에 있을 때만 오류가 발생합니다. 이는 매우 드문 일입니다.

각 코드워드 벡터는 그것에 디코딩되는 수신 코드워드 벡터의 관련 구를 가지며, 이러한 구들은 각각 코드워드에 고유하게 매핑되어야 한다.따라서 이러한 구들은 교차해서는 안 되기 때문에 우리는 구 채우기 문제에 직면해 있다.$n(displaystyle$ n$)$ 비트$$ 코드워드 벡터에 몇 개의 다른 코드워드를 포함할 수 있습니까?수신된 벡터의 최대 에너지는 $n{\displaystyle (P}$ ${\displaystyle +}$ $)$ {\$displaystyle$ n$(P$$+N)}$이므로 $반경n{\displaystyle \sqrt{(P}}$ $)$ {\$displaystyle {n(P$$N$)}}}의 구에 있어야 합니다.각 코드워드 구에는 $(\$이 있습니다.n차원 구체의 부피는 ${\displaystyle r^{}}$n {\$displaystyle$ r$^{n$에 정비례하므로 전송 강도 P로 우리 구에 채워질 수 있는 고유 디코딩 가능한 구체의 최대 수는 다음과 같습니다.

${\displaystyle {{n(P+N)}^{\frac {n}{{n}{2}}=2^{\frac {n}{2}}\log(1+P/N)},\!}$

이 인수에 의해 레이트 R은 $1{\displaystyle \frac{\mathrm{}}{}}$ ${\displaystyle 2}$ log "${\displaystyle }$( ${\displaystyle 1}$+${\displaystyle P}$ / N $)\display$ {$frac {$1$}$ ${2}}$ \$log$ ( 1 +$P$/ ${\displaystyle N}$ )$$。

달성 가능성

이 섹션에서는 마지막 섹션의 환율에 대한 상한 도달 가능성을 보여 줍니다.

인코더와 디코더 양쪽에 알려진 코드북은 길이 n의 코드워드 i.i.d를 선택함으로써 생성된다.$분산{\displaystyle }$P - ${\$ {$style$ P-$\epsilon}$ 및$$ 평균 0인 가우스.큰 n의 경우 코드북의 경험적 분산은 분포의 분산에 매우 가깝기 때문에 확률적으로 검정력 제약 조건의 위반을 피할 수 있습니다.

수신된 메시지는 고유하게 공통적으로 전형적인 코드북 내의 메시지로 디코딩된다.이러한 메시지가 없거나 전력 제약이 위반되면 복호화 오류가 선언됩니다.

Let ${\displaystyle X^{n}(i)}$ denote the codeword for message ${\displaystyle i}$, while ${\displaystyle Y^{n}}$ is, as before the received vector.다음 3가지 이벤트를 정의합니다.

1. $이벤트{\displaystyle }$U(\$displaystyle$ U$):$ 수신된 메시지의 파워가 P$(\displaystyle$ P$)$보다 큽니다.
2. $이벤트{\displaystyle }$V(\$displaystyle$ V$):$ 전송 및 수신된 코드워드는 공통적으로 일반적이지 않습니다.
3. $이벤트{\displaystyle {}_{}}$ ${\displaystyle E_{}}$j \ $displaystyle E_{j$ : (${\displaystyle {}^{}}$ ${\displaystyle n{}^{}}$( j${\displaystyle }$) , ${\displaystyle Y^{}}$n )$$\ $style$ ( $X ^$ { $n$} ($$$j$ ) ,Y$^{n}}$은 A${\displaystyle n_{}^{}}$( n $){$ $displaystyle$ $A_{\$$epsilon$$}^{(n$$)\}\}$에 $있습니다{\displaystyle {}_{}^{}}$.$여기$서 i$j$는 잘못된 코드워드가 수신된 벡터와 공통되는 전형적인 세트입니다.

따라서 U$\displaystyle$ U$,$ $\displaystyle$V 또는$$ $\$ $중{\displaystyle {}_{}}$ 하나가 발생하면$$ $오류$가 발생합니다.큰 숫자의 법칙에 따라 P$U)$ {{$displaystyle$ P$($$U)}$는 n이 무한대에 가까워지면 0이 되며, 공동 점근 등분할 특성에 따라 P${\displaystyle (}$${\displaystyle V}$$)$ {\$displaystyle P($V$)\}$에도 동일하게 적용됩니다. 따라서 충분히 큰$n{\displaystyle }$(\$displaystyle$ n$)$과 P$displaystyle$P(\) $모두.$$tyle$ P$(V)$는 $각각{\displaystyle }$ ${\(\displaystyle \epsilon$보다 작습니다.$i)$과 $j)(\displaystyle$ X$^{n}(j)$은 $(\displaystyle$ i$\neq$ j$)$에 대해 독립적이기 $때문$에 X$(\displaystyle$i$)$가 ${\displaystyle {됩니다}^{}}$.따라서 조인트 AEP에 $의해{\displaystyle }$P ( ${\displaystyle E_{}}$ ) ${\displaystyle ={}^{\mathrm{}}}$ -${\displaystyle n^{}}$ (${\displaystyle X^{}}$;${\displaystyle Y^{}}$) - ${\displaystyle {3\mu }^{}}$ $){$ $display$ P ( $E$_ { j } = 2$^{$- $n$( I ( X ; Y$)-3$ \ $epsilon$ 。$이것$에 ${\displaystyle {의해}_P^{}}$ ( ) n${\displaystyle {}_{}^{}}$_ $style$ P _ { e$$} （ I _ Y ; Y } ） （ ）$$$dent$ ) ） 。

$디스플레이 스타일P_{e}^{(n)}&\leq P(U)+P(V)+\sum _{j\neq i}P(E_{j})\&\leq \eq \epsilon +\sum _{j\neq i}2^{-n(I(X;Y)\epilon)&\silon}$

따라서 n이 무한대에 가까워지면 P${\displaystyle e_{}^{}}$ (${\displaystyle {}_{}^{}}$n $){$ $displaystyle$ P _ { $e$}^{ ($n$ )}는 0이 < ( ;) - 3$†$ ( \ $display$ R $< I$ ($X$ ; $Y$) - $3$ \ $epsilon$이 됩니다.따라서 R의 코드는 이전에 도출된 용량에 임의로 가깝습니다.

부호화 정리 역수

$이{\displaystyle }$ 예에서는 용량 ${\displaystyle C\frac{\mathrm{}}{}}$ ${\displaystyle =}$ ${\displaystyle \frac{1}{}}$ ${\displaystyle 2}$ log${\displaystyle \mu \frac{}{}}$( 1 + ${\displaystyle \frac{P}{}}$N$$){ $displaystyle$ C =$specfrac$ {1$}{2}}\$log($1+{\frac {P}{N$}}}}} $이상$의 환율을 달성할 수 없음을 보여 줍니다.

코드북에 대한 검정력 제약이 충족되고 메시지가 균일한 분포를 따른다고 가정합니다.W$(\displaystyle$ W$)$를 입력 메시지로 $하고{\displaystyle \stackrel{}{}}$ W$(\$를 출력 메시지로 $합니다{\displaystyle }$.따라서 정보는 다음과 같이 흐릅니다.

${\displaystyle W\long rightrow X^{n}(W)\long rightrow Y^{n}\long rightrow {W}$

Fano의 부등식을 활용하면 다음과 같은 결과를 얻을 수 있다.

$H$( ${\displaystyle W\stackrel{}{}^}$ )${\displaystyle 11}$ + ${\displaystyle n}$ R ${\displaystyle P_e^{}}$ (${\displaystyle {}_{}^{}}$n ) ${\displaystyle {}_{}^{}}$ ${\displaystyle n}$ ${\displaystyle {ϵ}_{}}$n \ $display style$H ($W$) \ $leq$1 + $nRP$_ { $e$${\displaystyle {}_{}^{}}$} $= n$ \ $epsilon$_ { $n$} ( ${\displaystyle n_{}^{}}$ )$여기$서 ${\displaystyle n_{}}$${\displaystyle {}_{}^{}}$${\displaystyle {}_{}}$\ $displaystyle$\$ilon$_ { $n$} \ $right$ ${\displaystyle {prow}_{}^{}}$ )

$($})를$$ 코드워드 색인 i의 부호화 메시지로 $합니다{\displaystyle {}_{}}$.그 후, 다음과 같이 입력합니다.

${\displaystyle{\begin{정렬}nR&, =H(W)\\&, =I(.{\hat{W}})+H(W{\hat{W}})\\&, \leq I(.{\hat{W}})+n\epsilon _{n}\\&, \leq I(X^{(n)};Y^{(n)})+n\epsilon _{n}\\&, =h(Y^{(n)})-h(Y^{(n)}X^{(n)})+n\epsilon _{n}\\&, =h(Y^{(n)})-h(Z^{(n)})+n\epsilon _{n}\\&, \leq \sum _ᆼ^ᆽh(Y_{나는})-h(Z^{(n)})+n\epsilon _{n}\\&, \leq\sum _{i=1}^.{n}I(X_{나는}.Y_{i}+n\epsilon_{n}\end{aligned}}$

$(\$를 인덱스 i의 코드워드의 평균 검정력으로 $합니다{\displaystyle {}_{}}$.

${\displaystyle P_{i}=black {1}{2^{nR}}\sum _{w}x_{i}^2}(w),\!}$

합계가 모든 입력 $메시지$에 걸쳐 있는 $경우,$ $(\$$$X_${i$$\})$와 $(\$})는$$ 독립적입니다.따라서 소음 $수준{\displaystyle }$N(\$displaystyle$ N$)$에 대한 $(\$})의 전력은 다음과 같습니다.

${\displaystyle E(Y_{i}^2})=P_{i}+N,\!}$

${\displaystyle {그리고}_{}}$ Yi$($디스플레이 $스타일$ Y_${i$})가$$ 정규 분포를 $따른다면{\displaystyle {}_{}}$

$\displaystyle h(Y_{i})\leq {frac {1}{2}}\log {2\pi e}(P_{i}+N)\!}$

그러므로,

${\displaystyle {begin{i}nR&\leq \sum (h(Y_{i})-h(Z_{i})}+n\epsilon _{n}\&\leq \sum \left\frac {1}{2}-{log1}-{\log1}-{\frac1}-{{\frac1}-{{{\fr}-{n}-{n}-{\displaysty}-{\fr}-{n}-{n}-{n}-{n}-{n}-{$

x의 오목함수인 ${\displaystyle \mathrm{로그}}$ of (${\displaystyle }$1 + $displaystyle \log ( 1$ + x $)\}$에$$Jensen의 등식을 적용하여 다음을 얻을 수 있습니다.

${{displaystyle {frac {1}{n}\sum _{i=1}^{2}\log \left(1+{P_{i}}{N}\right)\leq {1}{n}\log \left(1+{\frac {1}{n}\sum}_i={n}{n}$

각 코드워드는 개별적으로 전력 제약을 충족하기 때문에 평균은 전력 제약도 충족합니다.그러므로,

${\displaystyle {1}{n}\sum _{i=1}^{n}{\frac {P_{i}}{N}},\!}$

위의 불평등을 단순화하고 다음을 얻기 위해 적용할 수 있습니다.

${{displaystyle {1}{2}}\log \left(1+{\frac {1}{n})\sum _{i=1}^{n}{\right}\leq {frac {1}{2}\log \left(1+{\frac {P}{N}}\right}\,$

$따라서$ R${\displaystyle 1\frac{\mathrm{}}{}}$ ${\displaystyle \frac{1}{}}$ ${\displaystyle 2}$ log ${\displaystyle (}$ (${\displaystyle 1\mathrm{}}$ + ${\displaystyle P\frac{N}{}}$) + ${\displaystyle n_{}}$\ $display style$R \ $leq$\$left$( 1 + { \ $frac$ { $P }$ { $N }$ $}$ \ $log \$ left ( 1 + { \ frac {$$P } { N} } ) + \ $epsilon$ _ { $n$} to,,,,,,,,,, derived derived derived arbit derived derived derived derived derived derived derived derived derived $derived{\displaystyle {}_{}}$ 。

시간 영역에서의 효과

시리얼 데이터 통신에서는, 랜덤 지터(RJ)에 의해서 발생하는 타이밍 에러를 모델화하기 위해서, AWGN 수학적 모델을 사용합니다.

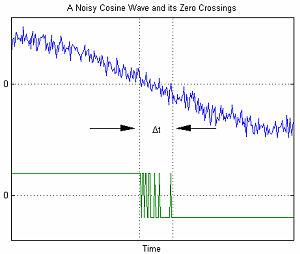
오른쪽 그래프는 AWGN과 관련된 타이밍 오류의 예를 보여 줍니다.변수 δt는 제로 크로싱의 불확실성을 나타냅니다.AWGN의 진폭이 커질수록 신호 대 잡음비는 감소합니다.이는 불확실성 δt를 ^[1]증가시킨다.

AWGN의 영향을 받는 경우 입력이 사인파일 때 협대역 통과 필터의 출력에서 초당 양 또는 음의 제로 교차 평균 수는 다음과 같습니다.

$(\displaystyle {\text{positive zero crossing}{\text{second}}=syslogfrac {\text{negative zero cross}}{\text{second}}}})$

$\displaystyle \displaystyle = f_{0}{\displayrt {{\text}SNR}}+1+{\frac {B^{2}}{12f_{0}^{2}}}{\text{\text}SNR}}+1}}},}$

어디에

f₀ = 필터의 중심 주파수,

B = 필터 대역폭,

SNR = 신호 대 잡음 전력 비율(선형).

위상 영역의 효과

현대 통신 시스템에서는 대역 제한 AWGN을 무시할 수 없습니다.위상 영역에서 밴드 제한 AWGN을 모델링할 때, 통계 분석에 따르면 실제 및 가상 기여의 진폭은 가우스 분포 모델을 따르는 독립 변수이다.결합 시, 결과 페이저의 크기는 Rayleigh 분포 랜덤 변수가 되며 위상은 0 ~ 2µ로 균일하게 분포됩니다.

오른쪽 그래프는 대역폭 제한 AWGN이 어떻게 간섭성 반송파 신호에 영향을 줄 수 있는지를 보여 줍니다.노이즈 벡터의 순간 응답을 정확하게 예측할 수는 없지만, 시간 평균 응답은 통계적으로 예측할 수 있다.그래프와 같이 노이즈 페이저는 1µ원 내에서는 약 38%, 2µ원 내에서는 약 86%, ^[1]3µ원 내에서는 약 98%가 될 것으로 자신 있게 예측하고 있습니다.

「 」를 참조해 주세요.

• 그라운드 바운스
• 노이즈 채널 부호화 정리
• 가우스 과정

레퍼런스