웨이브릿 변환

수학에서 웨이브릿 급수는 웨이브릿에 의해 생성된 특정 직교 정규 급수에 의해 제곱 적분 가능(실제 또는 복소값) 함수의 표현이다.이 문서는 직교 정규 웨이브릿과 적분 웨이브릿 ^{[1][2][3][4][5]}변환의 공식적이고 수학적인 정의를 제공합니다.

정의.

함수 $\delta {\displaystyle \delta {}^{}}$ $R)$ {\$displaystyle$ \psi \in $\L^{2}(\mathbb {R})}$는 ${\displaystyle {힐버트\mathrm{}}^{}}$공간 L2($)$ {\$displaystyle L2($왼쪽)에 대해 완전한 직교 정규 시스템인 힐버트 베이시스를 정의할 수 있는 경우 직교 정규 웨이브릿이라고 불린다.

Hilbert 베이스는 $함수{\displaystyle }$${\displaystyle }$패밀리 {{\$displaystyle \{\psi$_{$jk:},j,k,\in,\mathbb$ {Z$}}$의$$쌍방향 변환 및 확장을 통해 {\$displaystyle \psi$

${\displaystyle \psi _{jk}(x)=2^{\frac {j}{2}}\psi \left(2^{j}x-k\right)},$

$정수{\displaystyle }$ j${\displaystyle ,}$ ${\displaystyle k}$†$$ {\$style$ j$,,k,\in},\mathbb {Z$ 의 경우$.$

$($)의 표준 내부 제품$displaystyle$ L$^{2}\left(\mathbb {R}\right$에 있는 경우,

${\displaystyle f,g\rangle =\int _{-\infty }^{\infty }f(x){\overline {g(x)}}f(x})$

이 패밀리는 직교 정규 시스템입니다.

${\displaystyle {displaystyle \psi _{lm}\rangle &=int _{-\infty }^{\infty}\psi _{jk}(x){\overline {x}}}}\&=\displaystyle _{jl}\rangle _{km}\end}} 정렬됨$

여기서$$ ${\displaystyle j_{}}$ ${\displaystyle j_{}}$ l${\displaystyle {}_{}}$\ $displaystyle$\$delta$_ { $jl$} 은 Kronecker 델타입니다.

모든 $함수{\displaystyle }$ f${\displaystyle l{}^{}}$ L${\displaystyle {}^{}{2\mathrm{}}^{}}$ ( R$$) \ $displaystyle$ f , \ $in$, $L^{2}$ \ left ( \ $mathbb${ $R }$ \$right$ )를 다음과 같이 확장할 수 있으면 완전성이 만족됩니다.

${\displaystyle f(x)=\sum _{j,k=-\infty}^{\infty}c_{jk}\psi _{jk}(x)}$

직렬의 수렴이 표준 수렴으로 이해되는 경우.이러한 f의 표현을 웨이브릿 계열이라고 합니다.이는 직교 정규 웨이브릿이 자기 이중임을 의미합니다.

적분 웨이브릿 변환은 다음과 같이 정의된 적분 변환입니다.

$\displaystyle \left [W_{\psi }f\right](a,b)=param frac {1}{\paramrt {a}}}\int _{-\infty}{\infty}{\overline {psi \param {x-b}}}}}}{\f(x)}}}}}}:f(x)parampl,}$

다음으로 웨이브릿 ${\displaystyle {계수}_{}}$ c ${\displaystyle j_{}}$k(\$style c_{$jk})는$$ 다음과 같이 지정됩니다.

${\displaystyle c_{jk}=\left[W_{\psi }f\right]\left(2^{-j},k2^{-j}\right)}$

$여기$서 a ${\displaystyle =2^{}}$ -$$j {\$style$ a$=2^{-j}$는 2진수 확장 또는 2진수 확장, $b{\displaystyle }$ $=$ ${\displaystyle {\mathrm{}}^{}}$2 - ${\displaystyle j^{}}$ ${\$b$=k2^{-j}}$는 2진수 또는 2진수 위치이다.

원칙

웨이브릿 변환의 기본 개념은 변환이 시간 연장의 변경만 허용해야 하며 모양은 허용하지 않아야 한다는 것입니다.이는 ^[how?]이를 허용하는 적절한 기본 함수를 선택하는 것에 의해 영향을 받습니다.시간 연장의 변화는 기본 함수의 해당 분석 빈도를 준수할 것으로 예상된다.신호 처리의 불확도 원리에 근거하여

$\displaystyle \Delta \delta \geq \frac {1}{2}}$

$여기$서 t$${\$displaystyle$ t$}$는 시간을 나타내고$\omega {\displaystyle }$ \$displaystyle \obe }$ 각 주파수(${\displaystyle }$ ${\displaystyle =}$ ${\displaystyle 2}$ ${\displaystyle \mu }$f \$displaystyle \obe$=$2\pi$ f$)$입니다. $여기$서 f$${\$displaystyle$ f$}$는 일반 주파수입니다.

필요한 분해능이 시간 내에 높을수록 주파수의 분해능이 낮아져야 합니다.분석창의 확장이 선택될수록 ${\displaystyle \delta }$ t$$\ $displaystyle$\$Delta$t$$^[how?]값이 커집니다.

${\displaystyle \delta }$ t$$\ $displaystyle$\$Delta$ t$$$$, 、

1. 불량 시간 해결
2. 양호한 주파수 분해능
3. 저주파, 대규모 스케일링 팩터

${\displaystyle \delta }$ t$$\ $displaystyle$\$Delta$t가$$ 작을 때

1. 적절한 시간 해결
2. 잘못된 주파수 분해능
3. 고주파, 소형 스케일링 팩터

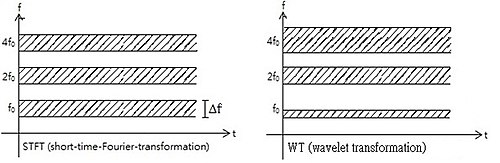
즉, 기본함수$\delta {\displaystyle }$ {$displaystyle \psi}$는 $함수{\displaystyle }$ x${\displaystyle (t)}${$display$ x$(t)}$가 필터링된 시스템의 임펄스 응답으로 볼 수 있다.변환된 신호는 시간과 주파수에 대한 정보를 제공합니다.따라서 웨이브릿 변환은 단시간-푸리에 변환과 유사한 정보를 포함하지만 기본 함수의 높은 분석 주파수에서 시간에 맞춰 나타나는 웨이브릿의 추가적인 특수 특성을 가지고 있다.푸리에 변환과 웨이브릿 변환의 상승 주파수에서의 시간 분해능 차이는 다음과 같습니다.단, 주파수 분해능은 시간 분해능이 증가하는 반면 주파수는 증가하므로 감소합니다.푸리에 불확도 원리의 이러한 결과는 그림에서 올바르게 표시되지 않습니다.

이는 웨이브릿 변환이 고주파의 시간 분해능에서 좋은 반면 느리게 변화하는 함수의 경우 주파수 분해능이 현저함을 보여줍니다.

또 다른 예는 다음과 같습니다.3개의 중첩 사인파 $신호{\displaystyle }$y (${\displaystyle \mathrm{t}}$ ) ${\displaystyle =}$ ${\displaystyle \sin }$ ${\displaystyle (}$ ( ${\displaystyle 2}$ ${\displaystyle {}_{}}$ ${\displaystyle {f\mathrm{}}_{}}$ 0${\displaystyle {}_{}}$) + ${\displaystyle \sin (}$ ( 4$$ f ${\displaystyle {0\mathrm{}}_{}{}_{}}$) + ${\displaystyle \sin }$ ( ${\displaystyle 8}$ ${\displaystyle {}_{}}$ ${\displaystyle {f\mathrm{}}_{}}$ 0${\displaystyle {}_{}}$) ( \ $displaystyle$y ( t ) \ ; = \ $sin$ ( $2$\ $pi f _${ 0 t ) \ + $0$; t ) ） 해석

웨이브릿 압축

Wavelet 압축은 이미지 압축(비디오 압축 및 오디오 압축도 가능)에 적합한 데이터 압축 형식입니다.눈에 띄는 실장은 JPEG 2000, 정지화면용 DjVu 및 ECW, JPEG XS, CineForm 및 BBC의 Dirac입니다.목적은 이미지 데이터를 파일에 가능한 한 작은 공간에 저장하는 것입니다.웨이브릿 압축은 무손실 또는 ^[6]무손실 중 하나입니다.

웨이브릿 변환을 사용하여 웨이브릿 압축 방법은 오디오의 타악음이나 2차원 영상의 고주파 성분, 예를 들어 밤하늘의 별 이미지 등의 과도현상을 표현하기에 적합하다.이는 데이터 신호의 과도 요소가 보다 광범위한 이산 코사인 변환과 같은 다른 변환이 사용되었을 때보다 적은 양의 정보로 표현될 수 있음을 의미합니다.

이산 웨이브릿 변환은 심전계(ECG) 신호의^[7] 압축을 위해 성공적으로 적용되었다. 본 연구에서는 연속된 심장 사이클 신호의 대응하는 웨이브릿 계수 사이의 높은 상관관계를 선형 예측을 사용하여 사용한다.

웨이브릿 압축은 모든 종류의 데이터에 효과적이지 않습니다.웨이브릿 압축은 과도 신호를 잘 처리합니다.그러나 부드럽고 주기적인 신호는 다른 방법, 특히 푸리에 관련 변환을 사용하는 주파수 영역의 기존 고조파 분석을 사용하여 더 잘 압축됩니다.일시적 특성과 주기적 특성을 모두 가진 데이터를 압축하려면 기존의 고조파 분석과 함께 웨이브릿을 사용하는 하이브리드 기술을 사용할 수 있습니다.예를 들어 Vorbis 오디오코덱은 주로 수정된 이산 코사인 변환을 사용하여 오디오를 압축합니다(일반적으로 부드럽고 주기적). 단,^[8] 과도 재생성을 개선하기 위해 하이브리드 웨이브릿 필터 뱅크를 추가할 수 있습니다.

x264 개발자의 가계부 참조: 비디오 압축을 위해 웨이브릿을 사용하는 현행 방법의 실제 문제를 논의하기 위한 웨이브릿(2010)의 문제점.

방법

우선 웨이브릿 변환을 적용한다.이렇게 하면 영상의 픽셀 수만큼 계수가 생성됩니다(즉, 변환일 뿐이므로 아직 압축은 없습니다).정보가 통계적으로 몇 개의 계수에 집중되기 때문에 이러한 계수를 더 쉽게 압축할 수 있습니다.이 원리를 변환 부호화라고 합니다.그 후 계수를 양자화하고 양자화된 값을 엔트로피 부호화 및/또는 런렝스 부호화한다.

웨이브릿 압축의 몇 가지 1D 및 2D 애플리케이션은 "웨이브릿 풋프린트"^[9][10]라고 불리는 기술을 사용합니다.

평가하기

이미지 압축 요건

대부분의 자연 영상의 경우 주파수가 낮은 스펙트럼 밀도가 ^[11]더 높습니다.그 결과, 상세 신호내의 정보는 폐기하면서, 저주파 신호(기준 신호)의 정보는 일반적으로 보존된다.영상 압축 및 재구성의 관점에서 웨이브릿은 영상 압축을 수행하는 동안 다음 기준을 충족해야 합니다.

• 보다 원래의 이미지를 기준 신호로 변환할 수 있습니다.
• 기준 신호를 기반으로 한 최고의 충실도 재구성.
• 기준 신호만으로 재구성된 영상에 아티팩트를 발생시키지 않아야 합니다.

시프트 분산 및 호출 동작에 대한 요구 사항

웨이브릿 영상 압축 시스템은 필터와 소멸을 포함하므로 선형 시프트-변수 시스템으로 설명할 수 있습니다.일반적인 웨이브릿 변환 다이어그램은 다음과 같습니다.

변환 시스템에는 2개의 분석 필터$displaystyle h_$${0$$}(n$$)$와 ${\displaystyle {하이패스\mathrm{}}_{}}$ 필터${\displaystyle }$h1$n)\displaystyle h_{$1}($$n)), 소멸 프로세스, 보간 프로세스 및 $$의 합성 ${\displaystyle {필터\mathrm{}}_{}}$g 0($)\$$displaystyle$$g_0(n)$ $및$ glays)가 있습니다$.$$tyle g_{1}(n)}$ 입니다.압축 및 재구성 시스템에는 일반적으로 영상 $압축용{\displaystyle {}_{}}$ 분석 필터 h ${\displaystyle {0\mathrm{}}_{}}$(${\displaystyle n}$) { $displaystyle h$_ { $0$$$（ $n$） the$$ the the the filters filters$$ filters ${\displaystyle {filters\mathrm{}}_{}}$ g${\displaystyle {}_{}}$0 (${\displaystyle n}$) { $displaystyle g$_ { 0 （ $n$） 。이러한 시스템을 평가하기 위해 $임펄스{\displaystyle }$( (${\displaystyle n}$ - $){$ $displaystyle$ $\delta$( n - $n$_$$${$ $i$$$} $)$를 입력하고 $재구성h{\displaystyle }$ ${\displaystyle (n}$ - ${\displaystyle {ni}_{}}$를 관찰할 수 있습니다.최적의 웨이브릿은 최소 시프트 분산과 심지어 h${\displaystyle }$(${\displaystyle n}$ - $ni ){$ $display$h ( $n-n_n_i$ )$이긴{\displaystyle }$ 하지만 severeltive wavelet입니다.h 엄격한 시프트 분산은 현실적이지 않으며 약간의 시프트 분산만 있는 웨이브릿을 선택할 수 있습니다.예를 들어, 다음 두 ^[12]필터의 시프트 분산을 비교할 수 있습니다.

웨이브릿 이미지 압축용 쌍직교 필터

		길이	필터 계수	규칙성
웨이브릿 필터 1	H0	9	.852699, .377402, -.110624, -.023849, .037828	1.068
	G0	7	.788486, .418092, -.040689, -.064539	1.701
웨이브릿 필터 2	H0	6	.788486, .047699, -.129078	0.701
	G0	10	.615051, .133389, -.067237, .006989, .018914	2.068

두 필터의 임펄스 응답을 관찰함으로써 두 번째 필터가 입력 위치에 덜 민감하다는 결론을 내릴 수 있습니다(즉, 덜 시프트 변형).

영상 압축 및 재구성의 또 다른 중요한 문제는 시스템의 진동 동작으로 재구성된 영상에서 원치 않는 심각한 아티팩트가 발생할 수 있습니다.이를 실현하기 위해서는 웨이브릿 필터의 피크 대 사이드 소브 비율이 커야 합니다.

지금까지 영상 압축 시스템의 1차원 변환에 대해 설명했습니다.이 문제는 2차원으로 확장될 수 있으며, 보다 일반적인 용어인 이동 가능한 멀티스케일 변환이 ^[13]제안된다.

임펄스 응답 유도

앞서 언급한 것처럼 임펄스 응답을 사용하여 영상 압축/재구성 시스템을 평가할 수 있습니다.

${\displaystyle \mathrm{입력}}$ $시퀀스x{\displaystyle }$(${\displaystyle n}$ ) ${\displaystyle =}$ ${\displaystyle (}$ (${\displaystyle n}$ - ${\displaystyle n_{}}$i$$) { $displaystyle$$$x ( n )$$$=$ \$$$display$ ( $n$${\displaystyle }$- n _ { $i$$$}$$∗ for ${\displaystyle {}_{}}$ r r r r r r r r r r r r r r r r r r （ n - n$$_ n _ n _ $n$_ n ）$r$ r r r $r$ r r $r$ r1$$( ${\displaystyle n}$$$) 。$_{0}(n)}$은(는) 로우패스 필터입니다.마찬가지로 다음 $기준신호{\displaystyle {}_{}}$ $n){$displaystyle $r_{2}(n)}$는 ${\displaystyle {r1\mathrm{}}_{}n)}$h $){displaystyle r_{1}(n)*h_{0}(n)}$에서 2배만큼 소멸한다.L레벨 분해(및 소멸) 후 분석응답은 2 $($${\displaystyle {\mathrm{표시스타일}}_{}^{}}$ $2^{L$${\displaystyle {\})}_{}^{}}$ $시료{\displaystyle {\mathrm{}}^{}}$ 중 ${\displaystyle {1개}_{}^{}}$($,$ ${\displaystyle {ni}_{}}$ $=$ ${\displaystyle f_{}^{}}$ h ${\displaystyle 0_L^{}}$ (${\displaystyle n}$- ${\displaystyle {ni}_{}}$/ ${\displaystyle 2^{}}$ L$)$ ({$표시스타일 h_{A}^{n_i})$를 유지하여 구한다.

한편, 신호 x(n)를 재구성하려면 기준 $신호{\displaystyle {}_{}{R}_{}}$ (${\displaystyle n)}$ ${\displaystyle =\delta }$ (${\displaystyle }$n - ${\displaystyle n_{}}$j$$) { $displaystyle$ r$_$ { $L$} ( n ) = \$delta$ ( n - n _ { $j$ 。상세 $신호{\displaystyle {}_{}}$ ${\displaystyle {di}_{}}$(${\displaystyle n}$ $){$ $displaystyle d_{ i }$ ( n )가 디스플레이 1$$ i i1 ≤1 ≤${\displaystyle 1}$ ${\displaystyle \le }$1 ≤1 ≤1 ≤1 ≤1 ≤1 ≤1 ≤1 ≤1 ≤1 ≤1 ≤1 ≤1 ≤1 ≤1 ≤1 ≤us 스테이지(${\displaystyle }$ -$$ \ $displaystyle L$${\displaystyle {}_{}}$-$$${\displaystyle 1_{}}$（${\displaystyle n}$ ）${\displaystyle {}_{}=\mathrm{g}}$ 0 ( ${\displaystyle {}_{}}$ -$$2 ${\displaystyle n_{}}$j ){ displaystyle $r$_ { L - 1 }$=$g _$$0 （ n ） $。$$이$는 $R$${\displaystyle {}_{}}$(${\displaystyle n}$)\ $displaystyle$ r$_$ { { l }( n$)$과 $0{\displaystyle {}_{}}$($n$)을 $보간하여{\displaystyle {}_{}}$ 얻을 수 있습니다.${\displaystyle L_{}^{}}$ -${\displaystyle }$2 ,${\displaystyle L}$ -${\displaystyle 3}$ ,${\displaystyle }$.${\displaystyle }$. ,$$1 ( \ $displaystyle$ $L$${\displaystyle {}_{}^{}}$-$2$ , L - 3 , $..$, 1$$)${\displaystyle {\mathrm{단계}}_{}^{}}$에서의 기준 $신호{\displaystyle }$ ${\displaystyle r}$${\displaystyle }$(${\displaystyle }$n ${\displaystyle {}_{}^{}}$ $displaystyle$r ($n$ , ${\displaystyle n_{}}$ ${\displaystyle {}_{}^{}{}_{}}$)${\displaystyle {}_{}^{}}$ f ${\displaystyle 0}$ (${\displaystyle {}_{}{displaystyle}_{}}$2 /$$)$\}:$ 기준 ${\displaystyle {신호}_{}}$ ${\displaystyle L}$($n$ ) { $displaystyle r_{L}($n$$)}과(와) 재구성된 신호와 관련이 있습니다$.$

전체적인 L레벨 분석/합성 시스템을 얻기 위해 분석 및 합성 응답을 다음과 같이 조합한다.

$display style$$$$AS}^{(L)}(n,n_{i})=\sum$ _${k}f_{$h0$}^{(L$)}($k-n_{i}/2^{$L})$f_{$g0}^{($L)(n/2^{L}-k$

마지막으로, 전체 임펄스 $응답{\displaystyle {}_{}^{}}$ h ${\displaystyle A_{}^{}}$ ${\displaystyle S_{}^{}}$( L${\displaystyle {}_{}^{}}$) ( ${\displaystyle n}$, ${\displaystyle n_{}}$i$$) \ $display style$ h$$_ {$AS}^{(L)}(n,n_{i}})$를 사용하여 웨이브릿 화상 압축 성능을 평가할 수 있다.

푸리에 변환 및 시간 주파수 분석과의 비교

변혁	표현	입력
푸리에 변환	${\displaystyle {X}(f)=\int _{-\infty}^{\infty}x(t)e^{-i2\pi ft},dt}$	$\displaystyle$ f$:$ 주파수
시간 빈도 분석	${\displaystyle X(t,f)}$	${\displaystyle t}${ $display style$ t$$} 시간$$$,$ $f{\displaystyle }$ { $style$ f$$} 주파수$$
웨이브릿 변환	${\displaystyle X(a,b)=syslogfrac {1}{\infty}{\infty}{\infty}{\overline {Psi \syslog\frac {t-b}{a}}}}}}}x(t)\d}$	${\displaystyle }$$b{\displaystyle }$시간 이동 계수$($time shift factor ($time$ shift factor$)$

웨이브렛은 특정 주파수를 조사할 때 계산을 줄일 때 푸리에 변환에 비해 약간의 이점이 있습니다.단, 이들 웨이브릿은 거의 민감하지 않으며, 실제로 공통 몰렛 웨이브릿은 수학적으로 가우스 ^[14]창 함수를 사용하는 단시간 푸리에 변환과 동일합니다.단, 알려진 비 사인파 형태(예: 심장박동)의 신호를 검색하는 경우는 예외입니다. 이 경우 일치하는 웨이브릿을 사용하면 표준 STFT/Morlet ^[15]분석을 능가할 수 있습니다.

기타 실용적인 응용 프로그램

웨이브릿 변환은 신호의 주파수와 그 주파수와 관련된 시간을 제공하므로 다양한 분야에서 매우 편리하게 적용할 수 있습니다.예를 들어 보행 분석,^[16] 고장 검출,^[17] 저전력 페이스메이커 설계 및 UWB(Ultra Wide Band) 무선 ^[18][19][20]통신용 가속 신호 처리입니다.

싱크로 재채기

싱크로 재채기 변환은 기존의 웨이브릿 ^[21][22]변환을 사용하여 얻은 시간 주파수 표현의 시간 및 주파수 분해능을 크게 향상시킬 수 있다.

「 」를 참조해 주세요.

• 연속 웨이브릿 변환
• 이산 웨이브릿 변환
• 복소 웨이브릿 변환
• 상수 Q 변환
• 정상 웨이브릿 변환
• 듀얼 웨이브릿
• 최소 제곱 스펙트럼 분석
• 다중 해상도 분석
• Los Alamos National Laboratory(LANL)의 오리지널 웨이브릿 압축 연구에서 개발된 이미지 형식인 MrSID
• 속도와 처리 효율을 위해 설계된 웨이브릿 기반의 지리 공간 이미지 형식인 ECW
• JPEG 2000, Wavelet 기반 이미지 압축 표준
• DjVu 포맷에서는 이미지 압축에 Wavelet 기반의 IW44 알고리즘을 사용합니다.
• 단시간 푸리에 변환 대신 웨이브릿을 사용하여 생성되는 스펙트럼의 일종인 스케일그램
• 웨이브릿
• 하르 웨이브릿
• 도베키 웨이브렛
• 이항 QMF(Daubechies 웨이브릿이라고도 함)
• 모렛 웨이브릿
• 개보르 웨이브릿
• 차플렛 변환
• 시간 빈도 표현
• S 변환
• 계층 트리에서 파티션 설정
• 단시간 푸리에 변환
• 영상 압축용 웨이브릿이 거의 코이플릿(거의 직교)일 수도 있음을 보여주는 바이오터럴 거의 코이플릿 기준입니다.

레퍼런스

^[1]

외부 링크

• Amara Graps (June 1995). "An Introduction to Wavelets". IEEE Computational Science & Engineering. 2 (2): 50–61. doi:10.1109/99.388960.
• Robi Polikar (2001-01-12). "The Wavelet Tutorial".
• René Puschinger의 웨이브렛 개요